复杂形状夹杂物对动车组车轮辋裂的影响

陈换过 蔡 丽 陈文华 陈 培 易永余 李雅洁

浙江理工大学机电产品可靠性技术研究浙江省重点实验室，杭州，310018

复杂形状夹杂物对动车组车轮辋裂的影响

陈换过 蔡 丽 陈文华 陈 培 易永余 李雅洁

浙江理工大学机电产品可靠性技术研究浙江省重点实验室，杭州，310018

以CRH5型动车组轮轴为研究对象，研究了夹杂物的形态对轮辋局部应力和轮辋裂纹成核的影响。结果显示，夹杂物棱角角度越小，夹杂物周围应力水平越高；夹杂物的厚度越小，半径越大，夹杂物周围最大等效应力越大，越易引起局部应力集中，导致疲劳裂纹易于萌生。利用有限元法和曲线拟合方法得到不同工况下夹杂物的临界尺寸，研究发现:不同工况下夹杂物的临界尺寸不同，弯道工况下的临界尺寸最小,夹杂物的尺寸超过临界尺寸时，裂纹才会萌生。

电动车组；车轮轮辋裂纹；夹杂物；形状因素；临界尺寸

0 引言

车轮轮辋裂纹(简称辋裂)是整体辗钢车轮中比较常见的故障之一。近年来，由辋裂引起的列车安全性问题成为影响铁路运输安全性和经济性的重大问题之一。对车轮辋裂的失效分析发现，车轮轮辋裂纹一般起源于踏面下10～20 mm处，并在接触载荷作用下沿轮辋周向扩展;绝大多数车轮辋裂源处发现有夹杂物的存在，可见夹杂物会影响车轮轮辋疲劳裂纹的产生[1]。因此，分析车轮轮辋内部夹杂物的尺寸对轮辋的疲劳性能和失效行为的影响，对列车的可靠运行有指导意义。

根据制造工艺的不同，车轮中材料缺陷的类型是多样的。典型的非金属缺陷包括MnS夹杂物、长条状砖炉衬残渣、SiO2夹杂物和Al2O3夹杂物。研究表明，影响轮辋裂纹萌生的一种典型且危害比较大的缺陷是带尖角的Al2O3夹杂物[2]。

近年来，为了了解夹杂物对车轮疲劳裂纹产生影响的机理，一些学者通过理论公式对夹杂物周围应力状态进行近似计算，并研究了夹杂物的尺寸参数和分布形态对车轮辋裂的影响机理。KABO等[3]研究发现，车轮材料缺陷能够引起显著的局部应力集中；他们分析了载荷级别、接触面几何特征和缺陷位置对缺陷萌生裂纹的影响，研究表明，接触面几何特征对疲劳性能的影响很小，载荷级别和缺陷位置需共同考虑，载荷级别越大，缺陷离踏面越近，引起的应力集中越明显，同时指出，如果两个或者多个缺陷相互之间距离很小时，裂纹会在缺陷之间迅速萌生和扩展。MARAIS[4]基于应变疲劳分析方法分析了车轮辋裂，当夹杂物引起的应力集中使最大剪切应力疲劳极限满足八面体剪切应力准则时，轮辋裂纹会萌生。XING等[5]研究了辗钢车轮辋裂问题，指出Al2O3夹杂物是辋裂萌生的重要原因；结合Murikami准则提出了疲劳极限与车轮维氏硬度以及夹杂物等效投影面积的关系式，通过此关系式可求萌生轮辋裂纹的临界尺寸。LANSLER[6]指出轮辋裂纹主要在微小缺陷处形成并扩展，并以含裂纹的车轮轮辋的一部分为研究对象，利用二维弹塑性有限元模型进行仿真分析，研究轮轨接触载荷级别和踏面形状对缺陷周围应力的影响。KABO等[7]利用弹塑性有限元方法研究车轮轮辋材料缺陷周围应力分布，通过弹塑性二维有限元模型分析不同尺寸的缺陷对车轮滚动接触疲劳的影响。

上述对夹杂物的研究多限于二维分析且将夹杂物简化为圆形。人们对工程实际中的车轮轮辋夹杂物的影响还缺乏认识，对复杂形状的夹杂物也未开展相关研究。为进一步了解夹杂物对车轮辋裂的影响机理，笔者在前期工作的基础上，主要分析了实际运行工况下Al2O3夹杂物(产生辋裂的典型夹杂物)与车轮轮辋裂纹萌生的关系，研究不同形状和尺寸的夹杂物对其周围轮辋的应力状态和对轮辋裂纹形核的影响规律，比较了车轮在直道、弯道和道岔等运载工况下轮辋夹杂物周围应力水平的高低，对不同工况下车轮轮辋萌生疲劳裂纹的夹杂物临界尺寸进行了计算。研究了夹杂物形态因素影响，确定了车轮运行载荷下可以引发疲劳开裂的夹杂物临界尺寸。

1 含夹杂物轮轴有限元模型

选择轮轴运行过程中的直道工况进行分析，轮轴所受载荷和约束条件按照国外标准UIC510-5规定的载荷工况设定，建立含夹杂物轮轴有限元模型进行分析。为模拟夹杂物对轮辋应力场的影响，基于有关资料[8]并作如下假设：①在车轮轮轨接触面正上方处存在夹杂物；②因夹杂物的存在，材料特性与周围单元不一致，故通过改变材料常数(弹性模量、泊松比)来模拟夹杂物的影响[9]。对车轮辋裂的失效分析发现，车轮轮辋裂纹一般起源于踏面下10～20 mm处，夹杂物大小不等。为研究方便，本文在距踏面10 mm处建立半径为100 μm的Al2O3夹杂物。为简化计算，近车轮踏面受接触力区域的基体选用弹塑性材料，远接触区域用弹性材料，即夹杂物周围基体用弹性材料,因为远接触区车轮基体应力远未达到材料的屈服极限。CRH5型动车组车轮轮辋的材料和Al2O3夹杂物的材料参数见表1。

表1 轮辋及夹杂物的材料参数Tab.1 Material parameters of rims and inclusion

根据结构对称的特点，建立1/4轮轴有限元模型。ANSYS中，夹杂物与车轮通过overlap命令建立关系。在车轴截面处和各剖切面上施加对称约束。由于车轮形状不规则，故采用自动划分网格，划分网格时选用三维实体单元SOLID187。与大体积的车轮相比，夹杂物体积很小，为了协调这两个尺寸之间的关系并提高计算结果的精确性，对夹杂物周围基体部分逐步以边长10 mm和20 mm的正六面体网格进行过渡细化。含夹杂物轮轴有限元模型及网格划分、约束和载荷的施加如图1所示。根据车轮直道行驶时的实际受力情况，对轮轴的有限元模型添加相应的边界条件。在轴颈上施加重力载荷，在轮轨接触处施加相应的垂向动载荷。根据标准UIC510-5可得垂向动载荷p与静载荷p0的关系p=1.25p0。

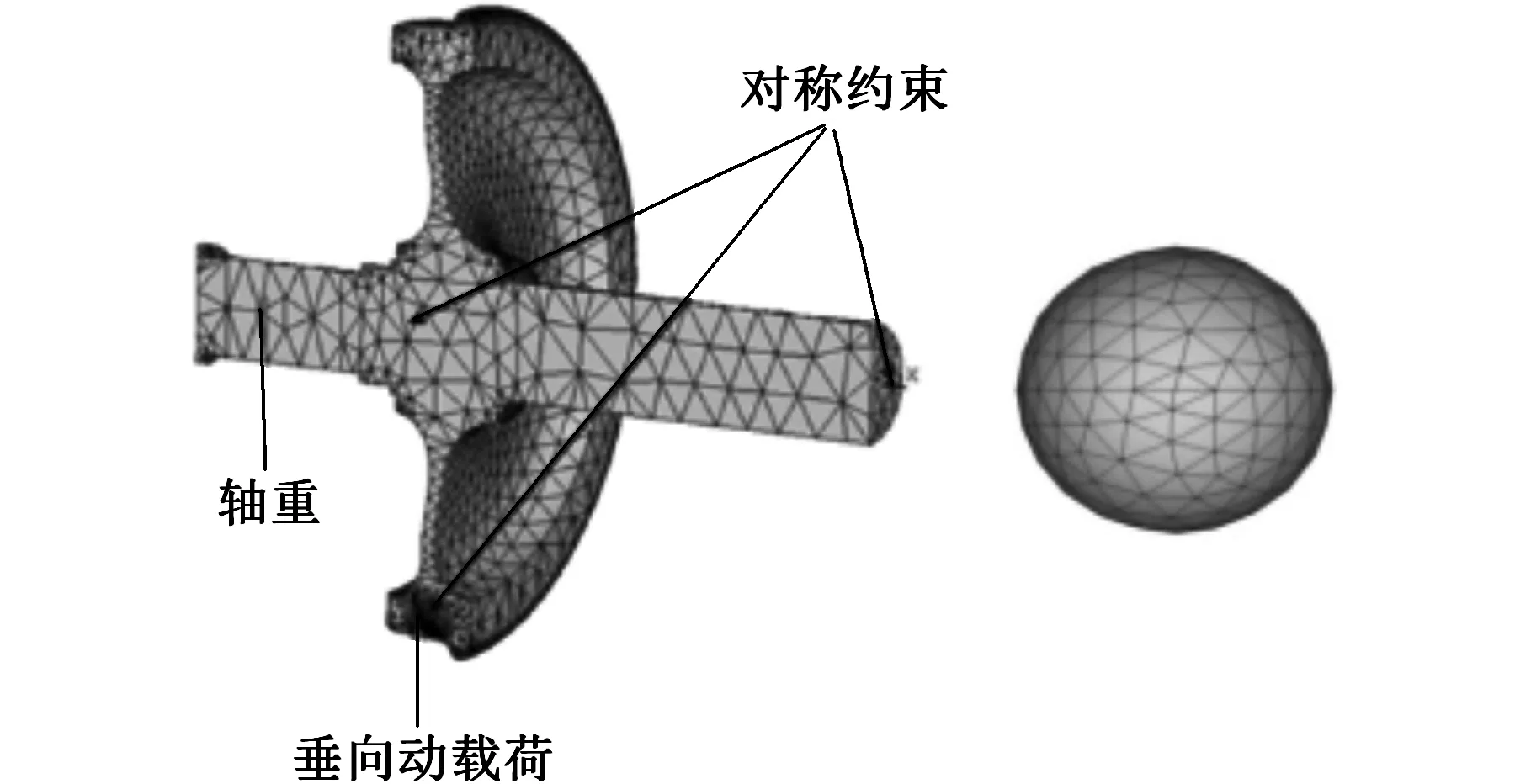
图1 车轮和夹杂物有限元模型Fig.1 Finite element model of wheel and inclusion

MI等[2]将夹杂物及其周围的轮辋材料等效为各向同性的线弹性材料，指出利用Goodier公式可计算出球形夹杂物周围基体的应力集中系数。轮辋中夹杂物处的应力集中系数为上下两极点处最大等效应力与轮辋施加在夹杂物的应力的比值。为了验证有限元方法的可行性，需要作如下计算。首先，根据文献[10]中Goodier公式计算图2夹杂物极点处应力,得到应力集中系数1.2206。然后，根据有限元法得到轮辋内部距踏面10 mm处球形夹杂物周围等效应力分布，如图2所示，最大等效应力约为319.523 MPa，轮辋作用于夹杂物的应力约为261.965 MPa。夹杂物的极点处存在应力集中，应力集中系数约为1.216。对比发现，仿真与理论的误差约为0.376%，由此可验证有限元方法分析夹杂物周围应力状态的可行性。表2所示为夹杂物网格划分时，不同单元尺度下，夹杂物应力集中系数值。由表2可知，在一定范围内，夹杂物的应力集中系数与单元尺度无关。

图2 夹杂物周围轮辋的等效应力分布Fig.2 Distribution of equivalent stress of rim around inclusion

夹杂物半径(mm)单元尺度级别120.101.215941.216090.151.216821.21713

2 夹杂物形状和尺寸因素分析

2.1 不同形状夹杂物应力状态分析

通过有限元法观察轮辋内部不同形状夹杂物周围轮辋材料的应力状态，分析夹杂物形状差异对夹杂物周围基体局部应力集中的影响。将不同形状的夹杂物分为两组：A组有6种形状的Al2O3夹杂物(图3)，其中，5种夹杂物为内角不同(60°，90°，120°，128.5°，135°)的正棱柱，1种为圆柱。这6种柱状夹杂物的截面内切圆半径均为0.1 mm，厚度均为0.1 mm。B组也有6种不同形状的Al2O3夹杂物(图4)，其中，5种为带尖角的不规则形状夹杂物，1种为球形夹杂物,这6种夹杂物的内切圆半径均为0.1 mm。

图3 柱形夹杂物Fig.3 Colum inclusions

图4 带尖角夹杂物和球形夹杂物Fig.4 Sphere inclusion and inclusions with point angle

利用有限元法得到棱柱形夹杂物周围轮辋基体的von Mises等效应力分布，图5为三棱柱夹杂物周围轮辋基体的von Mises等效应力云图。不同柱状夹杂物周围轮辋基体的最大von Mises等效应力见表3。

图5 三棱柱夹杂物周围基体von Mises应力分布Fig.5 Distribution of von Mises stress of matrix around triangular prism inclusions

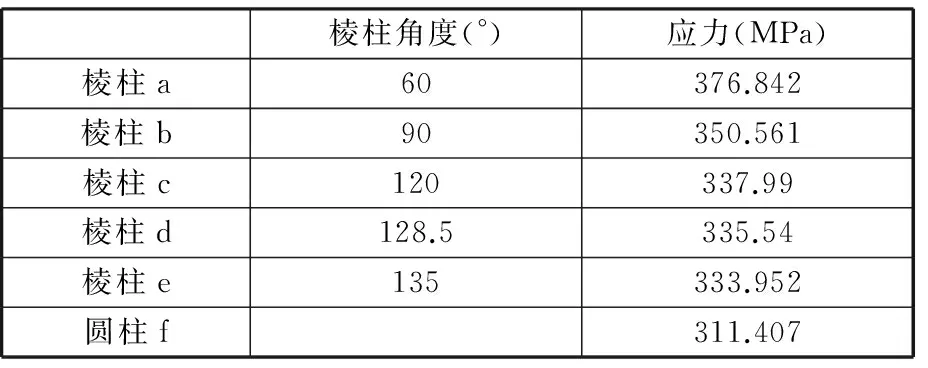
棱柱角度(°)应力(MPa)棱柱a60376.842棱柱b90350.561棱柱c120337.99棱柱d128.5335.54棱柱e135333.952圆柱f311.407

由图5和表3可知：①夹杂物周围轮辋基体最大等效应力点在夹杂物上顶点处。该处的等效应力明显大于其周围应力，最大等效应力点处存在应力集中现象。应力集中效应会使夹杂物与轮辋基体脱开或使Al2O3夹杂物自身破裂，在原夹杂物处形成空穴，进而使疲劳裂纹萌生。②棱柱夹杂物棱角角度与其周围轮辋基体最大等效应力成反比。

图6为不规则形状夹杂物周围轮辋基体的von Mises等效应力云图，不同棱锥形夹杂物周围轮辋基体最大von Mises等效应力见表4。

图6 带尖角不规则夹杂物周围基体 von Mises应力分布Fig.6 Distribution of von Mises stress of matrix around inclusions with irregular point angle

MPa

由图6、表4可知：①与柱形夹杂物对周围基体应力状态的影响规律类似，夹杂物周围轮辋基体最大等效应力点在夹杂物加载方向的尖角处。该处的等效应力明显大于其周围应力，最大等效应力点处存在明显的应力集中现象。②尖角形夹杂物顶角角度与其周围轮辋基体最大等效应力成反比。

2.2 夹杂物尺寸对周围基体应力状态的影响

以正三棱柱、正四棱柱和圆柱三种典型的夹杂物为例，研究夹杂物的大小对其周围轮辋基体应力状态的影响规律。棱柱夹杂物的尺寸因素为内切圆半径r和厚度L，夹杂物的位置和厚度L不变，改变夹杂物内切圆半径r，利用有限元法分别进行应力状态分析。

由图7可知，夹杂物为三棱柱和四棱柱，夹杂物内切圆半径从0.08 mm增大到0.30 mm时，周围轮辋基体的最大等效应力越来越大，且最小值和最大值相差很大。夹杂物为圆柱时，等效应力的变化很小。因此，在相同条件下，当夹杂物为棱柱时，随内切圆半径的增大，应力有显著的变化；当夹杂物为圆柱时，夹杂物半径在一定范围内对应力的影响很小。

图7 夹杂物内切圆半径对其周围最大等 效应力的影响Fig.7 Impact of inscribed circle radius of inclusions on maximal equivalent stress around inclusions

夹杂物的位置和内切圆半径不变，改变厚度L。每种形状的夹杂物水平方向的厚度依次为0.02 mm、0.05 mm、0.08 mm、0.10 mm、0.15 mm、0.20 mm和0.25 mm，共7组。夹杂物的大小对其周围轮辋基体最大von Mises等效应力的影响如图8所示。

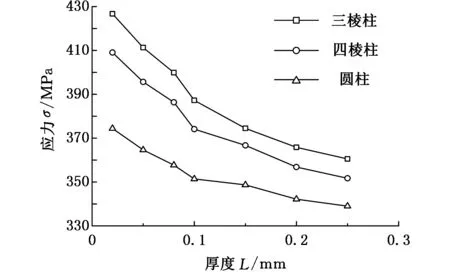
图8 夹杂物的厚度对其周围最大等效应力的影响Fig.8 Impact of thickness of inclusions on maximal equivalent stress around inclusions

从图8中可知，柱形夹杂物厚度增大时，夹杂物周围轮辋基体最大等效应力相应减小，当厚度达到一定值并继续增大时，等效应力不再明显变化。

文献[10]采用扫描电镜原位观测方法，动态跟踪观察了疲劳载荷作用下，不同形状和尺寸的夹杂物导致裂纹萌生、扩展乃至试样断裂的全过程，结果表明，不规则夹杂物在加载方向上的尺寸越大，疲劳裂纹萌生越早，试样寿命越短。该文献中的实验结果在一定程度上验证了本文的部分结论。

3 夹杂物临界尺寸计算

对夹杂物的形态和尺寸等因素的研究发现，和其他夹杂物相比，夹杂物为三棱柱时，其周围轮辋等效应力较大，引起的应力集中更加明显。因此有必要对这种形状的夹杂物临界尺寸进行研究。

3.1 含夹杂物轮辋材料疲劳极限的计算

相比于夹杂物尺寸而言，车轮轮辋可看作无限大体。对于含夹杂物的轮辋材料，当加载的疲劳载荷对应的最大应力为σ(MPa)、应力比R=1时，Murakami公式I型最大应力强度因子KImax为

(1)

其中，Q为位置常数，对于内部缺陷，Q=0.5；S为缺陷在垂直于加载方向的平面上的投影面积。

由Murakami公式知，应力强度因子门槛值

(2)

其中，P为位置常数，当夹杂物处于基体内部时P=2.77×10-3；HV为基体材料的维氏硬度。

令ΔKth=ΔK=2KImax，得疲劳强度：

σw=c(HV+120)/S1/12

(3)

其中，c为位置常数，当夹杂物处于基体内部时c=1.56。因此可得轮辋内部缺陷疲劳极限为

σw=1.56(HV+120)/S1/12

(4)

由式(4)可知，疲劳强度与投影面积成反比。夹杂物的尺寸越大，在与加载方向垂直的平面上的投影面积越大，疲劳强度就越小，因而越易使裂纹萌生和扩展。对于CRH5型动车组，轮辋材料的维氏硬度为HV300，则含正三棱柱夹杂物附近轮辋材料疲劳强度与夹杂物的半径关系式为σw=583/r1/6。

3.2 不同工况下含夹杂物轮辋内部最大主应力计算

在直道、弯道和道岔运行工况下，研究轮辋不同位置处夹杂物周围基体的最大主应力与夹杂物尺寸的关系。主要研究不同工况下距离踏面为10 mm和15 mm处的夹杂物，其半径从小到大依次取5 μm、10 μm、20 μm、30 μm、40 μm、50 μm、60 μm、70 μm、80 μm、90 μm、100 μm、150 μm、200 μm、250 μm和300 μm。利用有限元分析方法，分析每种情况下夹杂物周围应力的分布，提取出最大主应力。分别将踏面下10 mm处和15 mm处夹杂物周围基体最大主应力与夹杂物的半径对应的数据点导入MATLAB中，通过多项式拟合可得到函数曲线图。基于上述方法得到3种工况下距离踏面10 mm处和15 mm处夹杂物大小和最大主应力关系曲线，图9为直道工况，踏面下10 mm和15 mm处夹杂物大小与最大主应力关系曲线。

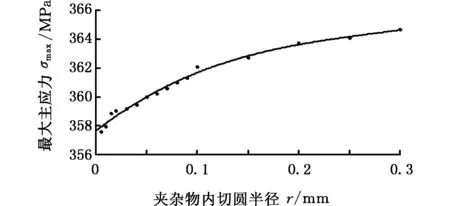
(a)夹杂物距踏面下10 mm处

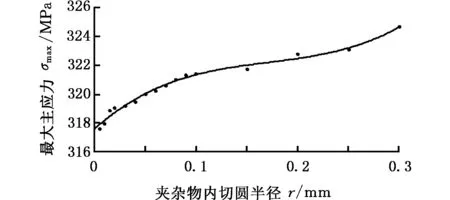
(b)夹杂物距踏面下15 mm处图9 夹杂物内切圆半径与最大主应力关系曲线Fig.9 Curve relations between inscribed circle radius of inclusions and maximal equivalent stress

3.3 临界尺寸计算

轮辋夹杂物的分布是没有规律的，其形状和大小不一，不同形状、不同大小的夹杂物对轮辋辋裂的影响也不同。根据3.1节可知，夹杂物周围轮辋材料的疲劳强度随着夹杂物大小的变化而变化。动车组车轮轮辋裂纹萌生的临界条件是某一位置夹杂物周围轮辋最大主应力超过疲劳强度。令轮辋最大主应力和疲劳强度相等可得到夹杂物的临界尺寸，当夹杂物的尺寸小于这个临界值时，夹杂物处裂纹将不会萌生，反之裂纹将会在裂纹处萌生。根据本文给出的轮辋材料疲劳强度与夹杂物尺寸的关系式，以及最大主应力与夹杂物尺寸的函数关系式，即可得到不同工况下、不同位置处夹杂物的临界尺寸，如图10～图12所示。表5所示为轮径890 mm、轴质量17 t时，不同工况下，轮辋距踏面10 mm和15 mm处夹杂物的临界尺寸。

图10 直道工况下的夹杂物临界尺寸Fig.10 Critical dimension of inclusions under straight track condition

4 结论

(1)夹杂物形状会对夹杂物周围的轮辋局部应力产生影响，对不同夹杂物进行分析发现，棱角角度越小，越易引起局部应力集中。

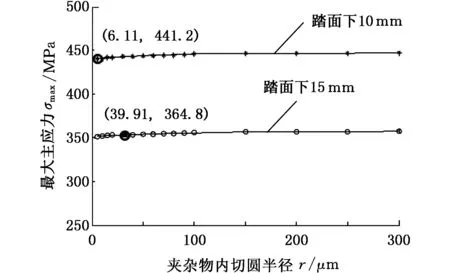
图11 弯道工况下的夹杂物临界尺寸Fig.11 Critical dimension of inclusions under curve track condition

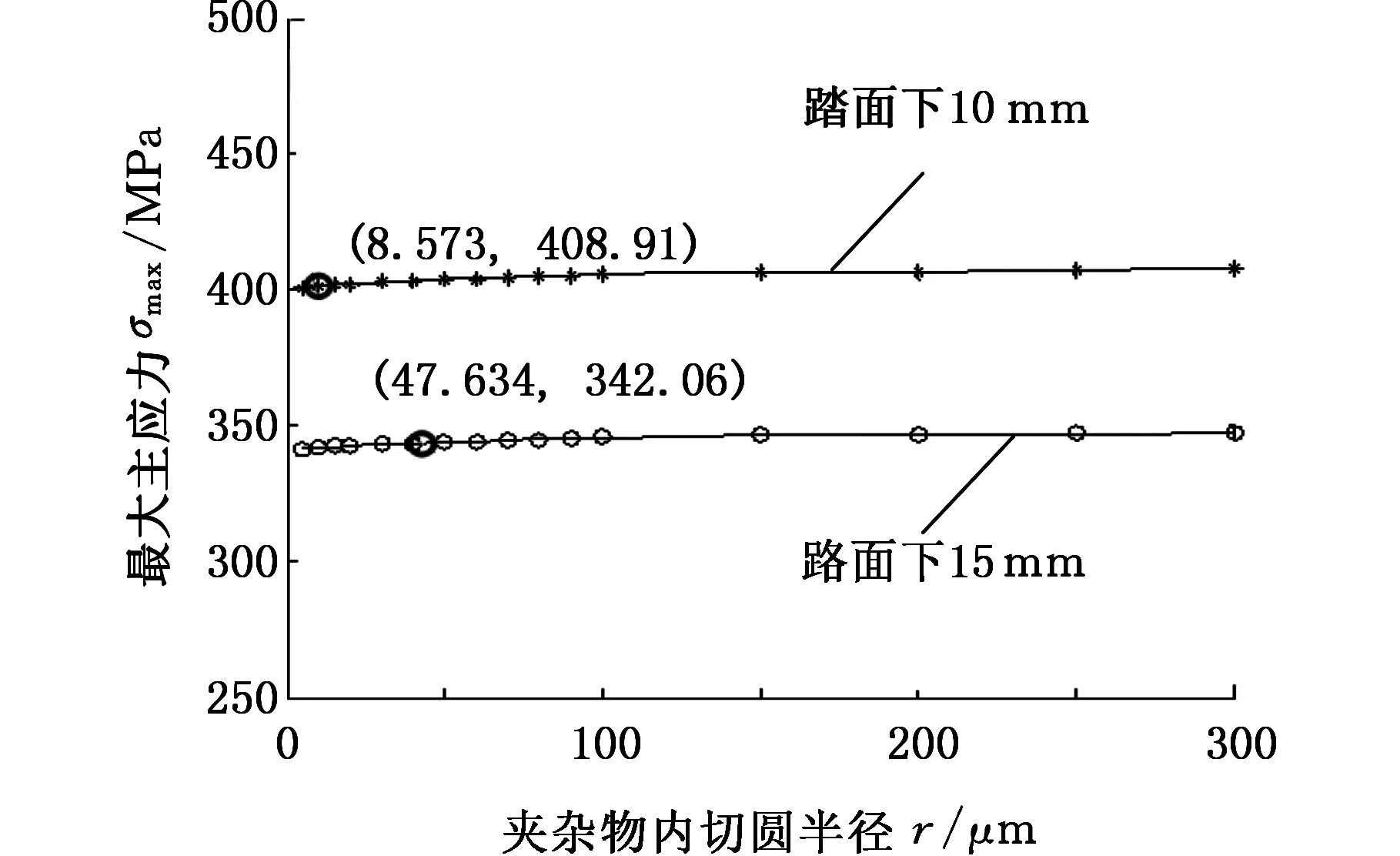
图12 道岔工况下的夹杂物临界尺寸Fig.12 Critical dimension of inclusions under turnout condition

μm

(2)夹杂物厚度一定时，增大内切圆半径，夹杂物周围等效应力变大；保持夹杂物的内切圆半径不变，夹杂物的厚度越小，夹杂物周围应力集中越明显。

(3)计算了3种工况下、不同踏面位置处夹杂物临界尺寸，比较可知，弯道工况下，车轮轮辋夹杂物临界尺寸最小；同种工况下，距踏面越近，夹杂物临界尺寸越小。

[1] 胡俊辉. 铁路客车轮对轮辋裂纹常见故障特征及原因分析[J]. 上海铁道科技,2014(1):78-79.

HU Junhui. The Cause Analysis and Fault Features of Railway Wheel Rim Crack[J]. Shanghai Railway Science Technology, 2014(1):78-79

[2] MI Guofa, NAN Hongyan. Influence of Inclusion on Crack Initiation in Wheel Rim[J]. Journal of Iron and Steel Research, 2011,18:49-54.

[3] KABO E, EKBERG A. Fatigue Initiation in Railway Wheels—a Numerical Study of the Influence of Defects[J].Wear, 2002,253:26-34.

[4] MARAIS J. Wheel Failures on Heavy Haul Freight Wheels due to Subsurface Defects[C]//Proceedings of the 12th International Wheelset Congress. Qingdao,1988：306-314.

[5] XING Lixian, ZHANG Yingzhi. Study on Rim Crack and Prevention[C]//Proceedings of the 12th International wheelset Congress. Qingdao,1988:53-58.

[6] LANSLER E. Subsurface Crack Face Displacements in Railway Wheels[J].Wear,2005,258:1038-1047.

[7] KABO E, EKBERG A. Material Defects in Rolling Contact Fatigue of Railway Wheels—the Influence of Defect Size[J]. Wear, 2005,258: 1194-1200.

[8] GERDUN V, SEDMAK T, SINKOVEC V, et al. Failures of Bearings and Axles in Railway Freight Wagons[J]. Eng. Fail. Analy., 2007, 14 :884-894.

[9] 冯磊. 非金属夹杂物对材料内局部应力集中的影响[J].机械工程学报，2013,49(8):41-48. FENG Lei. Effect of Non-metallic Inclusion on the Local Stress Concentration within Materials[J]. Journal of Mechanical Engineering,2013,49(8):41-48.

[10] 李少华.疲劳载荷作用下X80管线钢夹杂物的微观行为[J].石油学报, 2012,33(3):506-512． LI Shaohua. Micro-behaviors of Inclusions in the X80 Pipeline Steel under Futigue Lading[J]. Acta Petrolei Sinica, 2012,33(3): 506-512.

(编辑 张 洋)

Effects of Inclusions of Complex Shape on Cracks of Wheel Rim

CHEN Huanguo CAI Li CHEN Wenhua CHEN Pei YI Yongyu LI Yajie

Zhejiang Province’s Key Laboratory of Reliability Technology for Mechanical and Electrical Product, Zhejiang Sci-Tech University, Hangzhou，310018

Influences of inclusion shapes on local stresses and crack nucleation in CRH5 wheel rim were analyzed. Results show that the sharper of inclusion, the greater stress level of inclusion. Meanwhile, the local stress increases with the decrease of inclusion thickness and the increase of inclusion radius. And it leads to increase of local stress concentration factor. It indicates that fatigue cracks are produced easier and the reliability of the wheels is reduced. The critical inclusion sizes in different operating conditions were calculated by using FEM and curve fitting method. Results also show that the critical inclusion size changes followed by changes of the operating conditions. And the critical size is relative smaller when it is the curved track. Wheel rim fatigue cracking may be initiated once the inclusion size is bigger than the critical inclusion size.

electric motor unit(EMU); crack of wheel rim; inclusion; shape factor; critical size

2016-01-05

国家自然科学基金-高铁联合基金资助项目(U1234207)；国家自然科学基金资助项目(51475432)；浙江省自然科学基金资助项目(LZ13E050003)

TH123

10.3969/j.issn.1004-132X.2017.02.018

陈换过，女，1977年生。浙江理工大学机电产品可靠性技术研究浙江省重点实验室副教授。主要研究方向为结构健康监控、结构动力学及信号处理方法。发表论文40余篇。蔡 丽，女，1989年生。浙江理工大学机械与自动控制学院硕士研究生。陈文华(通信作者)，男，1963年生。浙江理工大学机电产品可靠性技术研究浙江省重点实验室教授、博士研究生导师。E-mail：chenwh@zstu.edu.cn。陈 培,男，1989年生。浙江理工大学机械与自动控制学院硕士研究生。易永余，男，1992年生。浙江理工大学机械与自动控制学院硕士研究生。李雅洁，女。1991年生。浙江理工大学机械与自动控制学院硕士研究生。