多物流配送中心的选址布局问题优化模型研究

李 明，刘 航，张晓建

(西南交通大学 交通运输与物流学院，四川 成都 610031)

多物流配送中心的选址布局问题优化模型研究

李 明，刘 航，张晓建

(西南交通大学 交通运输与物流学院，四川 成都 610031)

将生产商与销售商之间的直接供需关系纳入到多物流配送中心选址布局问题的研究当中，通过引入物流配送中心选建0～1变量，对现有一般运输问题的线性规划模型进行改进，从而建立多物流配送中心选址布局问题的非线性混合0～1规划模型，并通过lingo语言编程对该模型进行了求解，既实现了货物运输方案最优，也实现了物流配送中心选建数量最优，为多物流配送中心选址布局问题的解决提供一定的理论借鉴。

交通运输工程；多物流配送中心；选址布局；直接供需关系；优化模型

0 引 言

作为生产商与销售商的关键衔接平台，物流配送中心选址对于物流系统优化目标能否实现十分重要。由于物流配送中心拥有众多建筑物及固定的机械设备，一旦建成很难搬迁，如果选址不当，将付出严重的代价。因此物流配送中心选址对物流系统作用的发挥和经济效益的提升具有重要的影响，对选址问题的建模与求解一直以来都是学术界的热点[1]。丁浩等[2]通过对影响物流配送中心选址因素的分析，确立了影响物流配送中心选址的主要因素和原则，并以获得最佳经济效益为目标，建立了物流配送中心选址模型；吕海峰等[3]基于网络分析方法对物流配送中心选址问题进行了研究，建立了配送中心选址的网络优化模型，并通过总费用最小化确定配送中心的数量、位置以及生产商与配送中心、配送中心与销售商之间的供需关系，即最优供货方案；王晓博等[4]对电子商务环境下物流配送中心选址问题的特点和要求进行了系统的分析，将物流配送中心选址模型从变动费用和时间约束的条件进行修改，建立了适用于电子商务环境下的物流配送中心选址模型，并提出了定量化的启发式算法与定型化的综合评价法相结合来确定电子商务环境下配送中心选址的方法; A.HOBI等[5]应用重心方法对吉林省物流配送中心选址问题进行了研究；WANG Qingjun[6]通过对影响第三方物流配送中心选址布局问题相关因素进行分析，使用模糊综合评价法对第三方物流配送中心选址布局问题进行了研究；关菲等[7]在研究物流配送中心选址问题时，基于现有物流配送中心选址模型，结合模糊环境下影响物流配送中心选址的各因素，建立了以物流总费用最少，物流配送中心综合服务水平最高为目标的模糊多目标物流配送中心选址模型。

从上述研究成果来看，目前关于选址的模型只考虑了生产商与配送中心、配送中心与销售商之间的这种存在于生产商与销售商之间的间接供需关系(或间接供货方案)，而没有考虑到生产商与销售商之间的直接供需关系(或直接供货方案)，即生产商不经配送中心直接供货于销售商。基于此，笔者将生产商与销售商之间这一直接供需关系纳入到多物流配送中心选址布局问题研究当中，以运输成本最优为目标，通过引入物流配送中心选建0～1变量对现有一般运输问题的线性规划模型进行改进，建立了既能实现供货方案最优又能实现物流配送中心选建数量最优的非线性混合0～1规划模型。同时，只要对实际的一些多物流配送中心作相关处理，应用笔者所建模型在一定程度上也可回答物流配送中心有无必要选建这一问题。通俗言之，当模型的求解结果中，物流配送中心的最优选建数量为0时，同时也蕴含着生产商与销售商间没有必要修建物流配送中心这一层含义。

1 模型构建

选址问题的类型有很多，主要分为离散选址和连续选址两大类。所要研究的包括生产商与销售商之间直接供需关系在内的多物流配送中心选址布局问题是指从多个候选点对若干配送中心进行地址择优，以实现从生产商向销售商供货的运输成本最小化问题，属于离散选址问题。

1.1 问题描述与分析

现有m个生产商，p个销售商，以及拟建的n个物流配送中心。对于生产商来说，其既可以直接供应销售商，也可以通过物流配送中心间接供应销售商，各个配送中心之间不产生运量。试通过建立模型在运输成本达到最优的情况下，确定生产商与销售商之间的产品供应方案，并在拟建的n个物流配送中心中确定出最终要建设的q(q≤n)个物流配送中心。

去掉上述问题中生产商与销售商之间的物流配送中心，该问题就变成了一般的运输问题。对于运输问题，无论是理论研究、模型建立还是实际应用都已形成了完整成熟的体系。基于此，如何将现有求解运输问题的模型进行改进，从而用其来解决所要研究的问题，或者是如何将物流配送中心的选址问题转化成一般的运输问题，进而用一般运输问题的理论研究成果对其进行研究是笔者最初所想到的两种互为逆向的研究思路。当然，无论是物流配送中心选址问题还是一般的运输问题都有各自的特点，纵使相互转化也非绝对的相互转化。因此，笔者最终选用的研究思路为对物流配送中心选址问题进行类运输问题转化，然后结合物流配送中心选址问题自身的特点，对现有求解运输问题的模型进行改进，从而构建出求解物流配送中心选址问题的数学模型。

1.2 模型构建相关假设

1)物流配送中心的配送能力无上限。

2)物流配送中心工作的不确定因素多且较复杂。笔者在建模过程中只考虑生产商经物流中心向销售商配送的产品在配送中心的作业费用以及配送中心向各销售商配送产品的配送费用。用Mi(i=1，2，…，n)表示单位产品在物流配送中心i的作业费用，用Ni(i=1，2，…，n)表示单位产品在物流配送中心i的配送费用。

3)对于n个物流配送中心的建设成本，在建立模型时不予直接考虑，而是通过物流配送中心单位产品的作业费和配送费间接在模型中体现。也就是说，假设综合于选址等各方面因素在内的多个物流配送中心的建设成本的差异性，通过其单位产品的作业费用和配送费用之间的差异性来体现。

4)生产商的产量总和等于销售商需求量总和。

1.3 变量及参数定义

为了将物流配送中心选址布局问题转化为一般的运输问题，对于拟建的n个物流配送中心，采用求解带有中间转运站的运输问题时，对中间转运站所做的相关处理方法[8]，将其即视为生产商也视为销售商。因此对涉及到物流配送中心的部分相关参数以及变量不作单独的定义，而将其纳入到生产商与销售商中统一定义。

cij：从生产商所在地i至销售商所在地j单位产品运输费用；

xij：从生产商所在地i至销售商所在地j的运量；

ai：生产商i相关产品产量；

bj：销售商j对相关产品的需要量；

其中：i=1，2，…，m，m+1，…，m+n，j=1，2，…，p，p+1，…，p+n。

正如前述，i=m+1，m+2，…，m+n这n个数代表的即视为生产商处理的n个物流配送中心，同样j=p+1，p+2，…，P+n这n个数代表的即视为销售商处理的n个物流配送中心。

Mi：单位产品在物流配送中心i的作业费用；

Ni：物流配送中心i单位产品的配送费用；

yk：yk=1表示物流配送中心k建设，yk=0表示物流配送中心k不建设；其中：k=1，2，…，n，i=1，2，…，n。

1.4 模型建立

为了将物流配送中心选址布局问题转化为一般的运输问题，首先做如下两步处理：第一步，正如前述参数和变量定义中所述，将物流配送中心即视为生产商，又视为销售商；第二步，对于不经配送中心而直接由生产商i供应销售商j的单位产品运费按cij计算，对于经配送中心k由生产商i供应销售商j的单位产品运费，生产商i与配送中心k之间单位产品的运输费用按ci，p+k+Mk计算，配送中心k与销售商j之间单位产品运输费用按cm+k，j+Nk计算。

根据上述两步处理、前述相关参数和变量定义和产销平衡假设，可得物流配送中心选址布局问题的产销平衡运输表，如表1。

表1 物流配送中心选址布局问题的产销平衡运输

注：根据题设物流配送中心之间不产生运量易知xij=0，i=m+1，m+2，…，m+n，j=p+1，p+2，…，p+n，所以在后期的建模过程中不考虑这一部分运量，同样也无需考虑其相应的运费cij，i=m+1，m+2，…，m+n，j=p+1，p+2，…，p+n会带来的运输成本，于是即使令其运价均等于0也不会妨碍到模型的建立。

1.4.1 目标函数

物流选址布局问题所涉及到的运输成本主要分为直接运输成本和间接运输成本，直接运输成本是指不经配送中心由生产商直接供应销售商所消耗的运输成本，间接运输成本是指生产商经配送中心供应销售商所消耗的运输成本。因此所建模型以间接运输成本与直接运输成本之和达到最小为目标函数。

1)直接运输成本Fz

(1)

2)间接运输成本

(2)

3)目标函数

(3)

1.4.2 约束条件

1)生产商产量约束，即从生产商发往各配送中心以及各销售商的货物数量之和等于生产商的产量，生产商发出的货物总量等于生产商的产量。

(4)

2)销售商需求量约束，即各生产商以及各配送中心发往销售商的货物数量之和等于销售商的销量，销售商接收的货物总量等于销售商的销量。

(5)

3)物流配送中心相关约束，即物流配送中心的货物输入量等于其向外配送的货物量，也就是说流入物流配送中心的货物数量等于从物流配送中心流出的货物数量。

(6)

4)生产商的产量等于销售商的销量。

(7)

5)变量约束

xij≥0， i=1，2，…，m，m+1，…，m+n；

j=1，2，…，p，p+1，…，p+n；

yk=0或1， k=1，2，…，n。

1.4.3 最终模型建立

综上，可以得出物流配送中心选址布局问题的混合0～1规划模型。

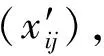
2 建模实例

现有5个生产商，4个销售商，以及拟建的3个物流配送中心。对于生产商来说，其既可以直接供应销售商，也可以通过物流配送中心间接的供应销售商，各个配送中心之间不产生运量。5个生产商的月生产能力(单位：件)分别为600，700，500，400，1 000，4个销售商的月销售量(单位：件)分别为800，900，900，600；其中拟建的3个物流配送中心的单位产品的作业费用(单位：元/件)为6，5，5，以及单位产品的配送费用(单位：元/件)为5，4，4。生产商、销售商、配送中心之间单位产品的运费如表2。试通过建立模型在运输成本达到最优的情况下，确定出该5个生产商与4个生产商之间的供应方案，并在拟建的3个物流配送中心中确定出最终要建设的q(q≤3)个物流配送中心。

表2 生产商、销售商、物流配送中心之间单位产品运费

注：①正如前述假设，在建模过程中将配送中心视为生产商处理也视为销售商处理，则表中销售商5，6，7以及生产商6，7，8均分别代表拟建的3个物流配送中心。 ②正如注①所述，cij=0，i=6，7，8，j=5，6，7。

根据上述分析，可得该问题的产销平衡运输表如表3。

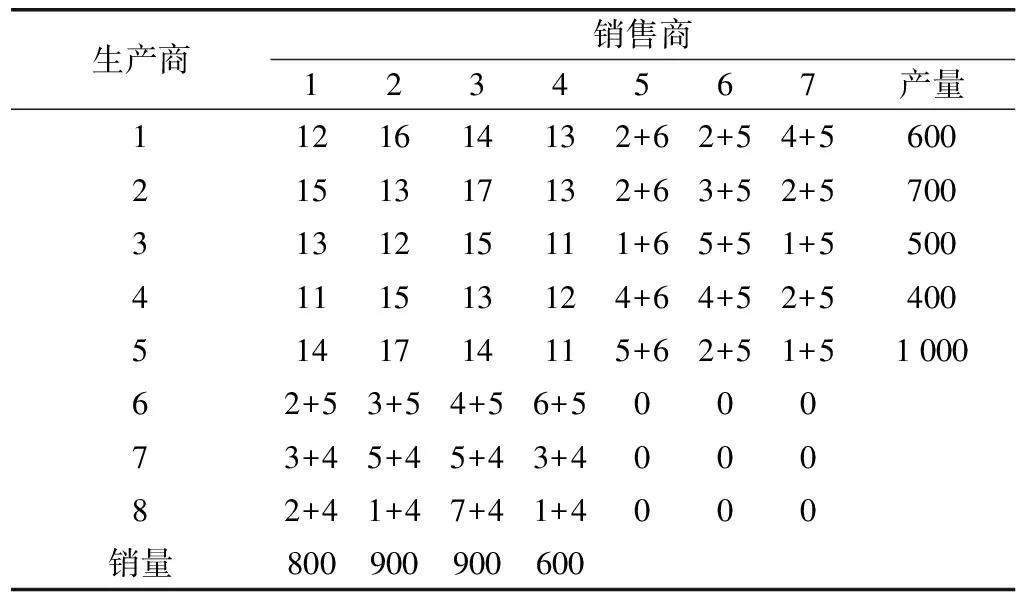
表3 产销平衡运输

从而建立该问题的混合0～1整数规划模型如下：

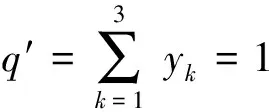
表4 最优货物运输方案

若按上述的配送中心建设方案进行建设，并按表4货物运输方案进行供货，可使成本达到最小值39 000元。

3 模型特点分析

笔者所建混合0～1规划模型是在充分分析物流配送中心选址布局问题的基础上，通过引入物流配送中心k选建0～1变量yk对现有求解一般运输问题的模型进行改进而得来的。相对于一般的多物流配送中心选址问题，所建模型有如下特点：

1)将生产商与销售商之间的直接供需关系纳入到多物流配送中心选址问题的建模与求解过程当中。

2)相对于一般的运输问题，根据物流配送中心选址布局问题的特点，所建混合0～1规划模型在目标函数与约束条件中引入0～1变量的同时也引入了非线性部分，这一点促使所建混合0～1规划模型相比于一般运输问题模型发生了质的改变，即相比于一般运输问题的线性规划模型，所建混合0～1规划模型属非线性数学规划模型。

3)所建模型以运输成本最优为目标，既能求解出运输成本最优的货物运输方案，也能求解出物流配送中心的最优选建数量，实现了双目标最优。

4 结 语

将物流配送中心选址布局问题语言数学化，由于问题规模大，而且复杂，因此一个低计算度模型的建立，能很大程度地提高问题的表述效率，同时也为问题的求解提供了有效的保证。基于这一思想，在充分分析物流配送中心选址布局问题的基础上，引入0～1变量对现有运输问题进行改进，从而建立了物流配送中心选址布局问题的非线性混合0～1规划模型。所建非线性混合0～1规划模型虽然能很好地描述多物流配送中心的选址布局问题，但相比于一般运输问题的线性规划模型，非线性却增加了模型的求解难度，因此如何通过数学语言将已经建立多物流配送中心选址布局问题的非线性混合0～1规划模型转化成线性的，从而利用现有成熟的线性规划模型求解算法对问题进行求解，将是笔者接下来要进一步研究的问题。

[1] 宾厚，单圣涤.物流配送中心选址模型及其算法分析[J].中国流通经济，2008(7)：16-18. BIN Hou, SHAN Shengdi. Analysis of logistics distribution center allocation model and algorithm[J].JournalofChinaBusinessandMarket, 2008(7)：16-18.

[2] 丁浩，李电生.城市物流配送中心选址方法的研究[J].华中科技大学学报，2004，21(1)：51-54. DING Hao, LI Diansheng. Study of the site selection method of city distribution center[J].JournalofHuazhongUniversityofScienceandTechnology, 2004，21(1)：51-54.

[3] 吕海峰，马维忠，王衍华.基于网络分析方法的物流配送中心选址的研究[J].运筹与管理，2004，13(6)：81-85. LV Haifeng, MA Weizhong, WANG Yanhua. A Study on the location selection of logistics distribution center based on the network analysis[J].OperationsResearchandManagementScience, 2004，13(6)：81-85.

[4] 王晓博，李一军.电子商务环境下物流配送中心选址模型与评价方法[J].系统工程理论方法应用，2006，15(3)：200-204. WANG Xiaobo, LI Yijun. Research on logistics distribution center location model and evaluation under electronic commerce[J].SystemsEngineering-TheoryMethodologyApplications, 2006，15(3)：200-204.

分节？2012，7(8)：1799-1806.

[5] HOBI A，BIHL T，FELLAYB，et al. Study on logistics center site selection of jilin province[J].JournalofSoftware, 2012，7(8)：35-39.

[6] WANG Q J，WANG X B，WANG Q Q. Study on site selection method of third-party logistics distribution[J].Appliedmechanics&Materials, 2013，310：614-618.

[7] 关菲，张强.模糊多目标物流配送中心选址模型及其求解算法[J].中国管理科学，2013，21：57-62. GUAN Fei, ZHANG Qiang. A fuzzy multi-objective logistics distribution center location model and its solution algorithm[J].ChineseJournalofManagementScience, 2013，21：57-62.

[8] 焦永兰.管理运筹学[M].北京：中国铁道出版社，2010：94-97. JIAO Yonglan.ManagementOperationResearch[M].Beijing: China Railway Publishing House, 2010：94-97.

(责任编辑 朱汉容)

Research on the Optimization Model of Site Selection and Layout of Logistics Distribution Center

LI Ming，LIU Hang，ZHANG Xiaojian

(School of Transportation and logistics, Southwest Jiaotong University, Chengdu 610031，Sichuan, P.R.China)

The direct relationship of supply and demand between manufacturer and retailer was brought into the research on the site selection and layout of logistics distribution center, and constructed the nonlinear mixed 0～1 programming model of the site selection and layout of logistics distribution center was conducted through improving the linear programming model of existing general transportation problem with introducing the 0～1 variable of the selection of logistics distribution center. At last, the optimal solution of freightage and the optimal number were obtained, by which the logistics distribution center will be constructed by solving this model with LINGO. Thus, to solutionssuch issues as the site selection and layout of logistics distribution center were put forward.

traffic and transportation engineering; logistics distribution center; site selection and layout; the direct relation between supply and demand; optimization model

10.3969/j.issn.1674-0696.2017.01.18

2015-11-09；

2016-01-05

四川省软科学研究计划项目(2015ZR0120)

李 明(1978—)，男，汉族，四川人，副教授，博士，主要从事运输经济与物流经济方面的研究。Email: mingli@home.swjtu.edu.cn。

U125

A

1674-696(2017)01-097-06