基于改进Shapley值法的建设项目交通影响费用分配

闫冬梅，冯树民，邵毅明

(1.东南大学 交通学院，江苏 南京 210000；2.哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 150400；3.重庆交通大学 交通运输学院，重庆 400074)

基于改进Shapley值法的建设项目交通影响费用分配

闫冬梅1，冯树民2，邵毅明3

(1.东南大学 交通学院，江苏 南京 210000；2.哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 150400；3.重庆交通大学 交通运输学院，重庆 400074)

通过对交通影响费用分配的影响因素进行分析，在Shapley值法的基础上，考虑交通运行、交通组织和交通安全等影响因素，运用层次分析法计算各影响因素权重，确定交通影响因子，建立改进Shapley值法的交通影响费用分配模型。最后以某区域3个企业为例，对各企业间的交通影响费用进行合理分配。结果表明：该模型计算简单，具有一定的可操作性。

交通工程；影响费用；影响因子；Shapley值；AHP；权重

随着我国社会经济的快速发展，城市化进程不断加快，促进了许多新项目的开发和建设。新建的项目会诱发增加新的交通需求，这将会导致新建项目周围地区的交通运行效率下降，甚至会降低整个路网的服务水平。因此，为改善这些区域的交通运行状况和交通服务水平，需要进行交通基础设施的建设。并向开发商合理征收因其项目开发而增加的全部或部分交通基础设施建设和改造费用，这对筹措交通基础设施建设资金、缓解城市交通拥堵有着十分重要的作用。而交通影响费用合理分配有助于交通影响费收取工作的有效实施。

Shapley值法为交通影响费用的合理分配提供了有效方法[1-2]。近年来，不少学者根据实际情况，对Shapley值法做了相应改进。例如：张智勇等[3]分析了Shapley值法在港口物流服务供应链的利益分配中的不足，并首次提出了Shapley值法的改进模型；黄炜等[4]等充分考虑了各合作企业的风险、投资和物流能力等方面影响因素，建立了基于综合修正因子的Shapley值法改进模型；宋静等[5]引入了区间值模糊支付Shapley值法，对战略网络的收益进行分配；谢国辉等[6]综合考虑各电厂在协同报价中的贡献程度、风险和阻塞等影响利润分配结果的因素，建立了具有修正因子的改进Shapley值分配模型；魏学文等[7]在国内外研究的基础上，引入综合影响因子的概念，应用模糊综合评价法对传统的Shapley值法进行改进。

笔者在这些学者的研究基础之上，综合考虑交通运行、交通组织和交通安全等影响因素，建立了基于交通影响因子的改进Shapley值法的交通影响费用分配模型，对各建设企业间的交通影响费用进行合理分配。

1 Shapley值法的基本模型及其改进

1.1 Shapley值法的基本模型

Shapley值法给交通影响费用的分配提供了公平合理的方案，分配结果易被所有开发企业接受。

因此，分配给合作企业中i的费用可用Shapley值公式表示：

i=(1，2，…，n)

(1)

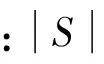
1.2 Shapley值法的改进模型

传统的Shapley值法没有考虑交通影响费用分配的其他因素。因此，笔者从交通运行、交通组织和交通安全等3方面入手[8]，综合考虑交通影响费用分配的影响因素，并计算各因素在交通影响费用分配中所占的权重，再将加权因子合成到Shapley值的计算方法中，得到改进的Shapley值法模型。建设项目交通影响费用分配影响因素指标体系为3个2级指标和9个3级指标[9]，如图1。

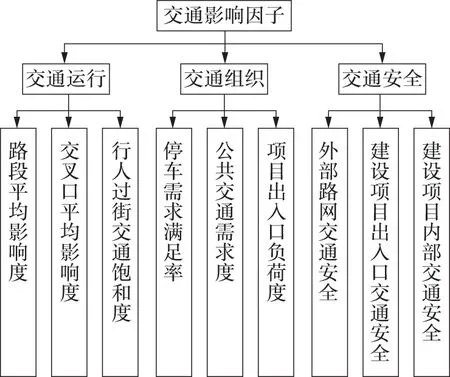
图1 交通影响费用分配影响因子Fig.1 Factors impacting traffic impact fee allocation

假设有n个交通影响费用分配合作企业N=( x1， x2，…，xn)，交通影响产生的总费用为c(N)，采用传统Shapley值法求得企业i的费用分配额为xi，计算出交通影响因子，并对传统的Shapley值法进行改进，计算出改进的费用分配值。

具体步骤如下：

1)运用AHP方法得出影响交通费用分配的3个子因素[10]，即路段平均影响度、交叉口平均影响度、行人过街交通饱和度的权重向量α=(α1，α2,α3)，依据专家评分法得到3个企业的影响因素系数模糊矩阵d1，计算可得交通运行影响因素向量为D=αd1。同理，计算可得交通组织影响因素向量为J=βd2；交通安全影响因素向量为H=γd3。

2)分别算出交通运行、交通组织和交通安全的修正因子ΔD=D-1/n，ΔJ=J-1/n，ΔH=H-1/n。

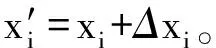
2 案例计算

笔者以某区域的3个建设企业为例。这3个企业需要交的交通影响总费用为115万元，运用Shapley值法将这部分费用分配到3个企业中去。3个合作企业分别用1，2，3来代替，根据其他合作企业费用支出数据资料，并参考专家对建设项目的分析预测，预计合作企业中各个企业的费用如下：

c(1)=58，c(2)=62，c(3)=65，c(1，2)=85，

c(1，3)=88，c(2，3)=92，c(1，2，3)=115。

2.1 传统Shapley值法的费用分配

2.2 改进Shapley值法的费用分配

2.2.1 影响因素的系数计算

根据权重系数和模糊矩阵，计算3个企业交通运行影响因素向量为：

根据权重系数和模糊矩阵，计算3个企业交通组织影响因素向量为：

根据权重系数和模糊矩阵，计算3个企业交通安全因素向量为：

2.2.2 交通影响因子及修正值的计算

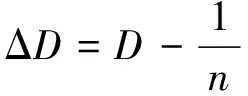
0.086 7，-0.093 3)

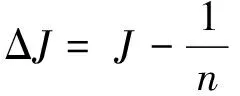
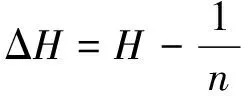
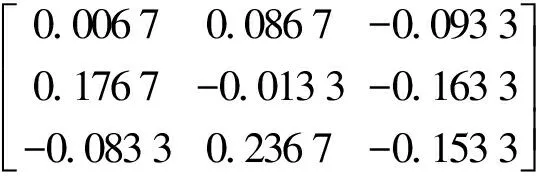
=(0.090 7，0.056 7，-0.147 4)

影响值为：Δx1-115×0.090 7=10.430 5，Δx2=115×0.056 7=6.520 5，Δx3=115×(-0.147 4)=-16.951。

2.2.3 费用分配值

综合前面计算，可以求得3个企业费用分配值如下：

2.3 两种费用分配方案比较

通过传统的Shapley值分配方案与改进的Shapley值分配方案的比较，如表1。由表1可以看出，在改进的Shapley值分配方案中，企业1的费用增加了10.430 5万元，企业2的费用增加了6.520 5万元，而企业3的费用减少了16.951万元。说明企业1和企业2对社会、交通、环境的影响较大，而企业3的交通影响费用降低，表明该企业的建设项目产生的交通影响较小。改进shapley值法的费用分配考虑了建设项目的实际交通影响，使各企业交通影响费用分配结果更加公平、合理。

表1 两种模型方法费用分配方案比较

3 结 语

笔者综合考虑交通影响费用分配的影响因素，从交通运行、交通组织和交通安全等3方面选取具有代表性的指标。并计算交通影响因子，同时对传统的shapley值法进行改进。最后通过实例计算，得出两种方法的交通影响费用分配方案，并对费用分配结果进行比较，结果表明：运用改进Shapley值法对交通影响费用分配进行研究，使交通影响费用分配结果易为所有建设企业接受，具有一定的实际应用价值。

[1] 卓翔芝，王旭，王振锋.供应链联盟伙伴合作关系的进化博弈研究[J].计算机工程与应用，2010，46(1)：208-210. ZHUO Xiangzhi, WANG Xu, WANG Zhenfeng. Study on evolution game of supply chain alliance companionate symbiosis[J].ComputerEngineeringandApplications, 2010，46(1)：208-210.

[2] SHAPLEY L S.A value for n-persons games[J].AnnalsofMathematicsStudies, 1953(28)：307-318.

[3] 张智勇，郑成华，宋薛峰.基于改进Shapley值的港口物流服务供应链利益分配分析[J].工业技术经济，2009，28(6)：113-115. ZHANG Zhiyong, ZHENG Chenghua, SONG Xuefeng. Study on port logistics service supply chain revenue distribution based on improved Shapley value method[J].IndustrialTechnologyEconomy, 2009，28(6)：113-115.

[4] 黄炜，龚本刚.基于改进Shapley值法的汽车零部件循环取货收益分配研究[J].安徽工程大学学报，2012，27(1)：90-94. HUANG Wei, GONG Bengang. Research on income distribution of automobile parts milk-run based on improved Shapley value[J].JournalofAnhuiPolytechnicUniversity, 2012，27(1)：90-94.

[5] 宋静，阮平南.基于改进Shapley值法的企业战略网络收益分配[J].科技管理研究，2012(1)：99-101. SONG Jing, RUAN pingnan. Profit allocation in strategic network based on improved Shapley value[J].ScienceandTechnologyManagementResearch, 2012(1)：99-101.

[6] 谢国辉，张粒子，邵志刚等.改进Shapley值在协同报价利润分配中的应用[J].华东电力，2009，37(2)：232-235. XIE Guohui, ZHANG Lizi, SHAO Zhigang, et al. Application of improved Shapley value to profit distribution for collaborative bidding[J].EastChinaElectricPower, 2009，37(2)：232-235.

[7] 魏学文，李文涛.基于改进Shapley值法的供应链联盟利益分配研究[J].统计与决策，2010(23)：104-106. WEI Xuewen, LI Wentao. The study of profit allocation among partners in supply chain alliance based on improved Shapley value[J].StatisticsandDecision, 2010(23)：104-106.

[8] 闫冬梅，向红艳，邵毅明，等.城市轨道交通换乘站运行效率评价[J].重庆交通大学学报(自然科学版)，2013，32(1)：99-102. YAN Dongmei, XIANG Hongyan, SHAO Yiming. et al. Operating efficiency evaluation of city rail transit station[J].JournalOfChongqingJiaotongUniversity(NaturalScience), 2013，32(1)：99-102.

[9] 李燕，徐维祥.建设项目交通影响程度模糊评价研究[J].公路，2008(5)：104-109. LI Yan, XU Weixiang. Fuzzy evaluation on traffic impact degree of urban construction project[J].Highway，2008(5)：104-109.

[10] 张东东.中小城市交通影响评价研究[D].重庆：重庆交通大学，2014. ZHANG Dongdong.ResearchonTrafficImpactanAnalysisfortheMedium-SmallCities[D]. Chongqing: Chongqing Jiaotong University, 2014.

(责任编辑 刘 韬)

Traffic Impact Fee Allocation of Construction Project Based on Improved Shapley Value Method

YAN Dongmei1，FENG Shumin2，SHAO Yiming3

(1. School of Transportation, Southeast University, Nanjing 210000, Jiangsu, P.R.China；2.School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150400, Heilongjiang, P.R.China；3.School of Traffic & Transportation, Chongqing Jiaotong University, Chongqing 400074，P.R.China)

The trafic impact factors were determined by analyzing the influences on traffic fee allocation, by Shapley value method and by considering such influences as traffic operation, traffic organization and traffic safety. The hierarchy analysis method was used to calculate weights of each of the various influencing factors. The traffic fee allocation model was established by means of improved Shapley value method. Finally three enterprises of certain one area were taken as examples to make reasonable allocation of traffic impact fees among the three enterprises. The results show that this model is easy and operable in some degree.

traffic engineering; impact fee; impact factor; Shapley value; AHP; weight

10.3969/j.issn.1674-0696.2017.01.17

2015-08-27；

2015-12-03

黑龙江省交通运输厅基金项目(GC13D507)

闫冬梅(1988—)，女，黑龙江哈尔滨人，博士研究生，主要从事交通运输规划与管理方面的研究。E-mail: ydm_1988@163.com。

U491.1

A

1674-0696(2017)-093-04