基于反馈调节函数投影同步的混沌保密通信研究*

陈镜伯 冯 平 唐 宏 陈杰睿

(后勤工程学院机械电气工程系 重庆 401311)



基于反馈调节函数投影同步的混沌保密通信研究*

陈镜伯 冯 平 唐 宏 陈杰睿

(后勤工程学院机械电气工程系 重庆 401311)

为进一步提高混沌保密通信的安全性,应用Lyapunov稳定性定理以及反馈调节方法,在函数投影同步的基础上提出了反馈调节函数投影同步,将此方法应用于混沌掩盖方案中,通过数学推导和Matlab数值仿真,证明了其有效性和可行性。

混沌保密通信; 反馈调节函数投影同步; 混沌掩盖

Class Number TP273

1 引言

自1963年气象学家Lorenz发现混沌现象以来,混沌得到了广泛而深入的探索和研究,混沌也被称为20世纪以来继量子力学、相对论之后的第三大科学理论革命,被誉为是连接两者之间的桥梁,同时更是连接确定论与随机论之间的一个重要理论。而自1990年美国海军实验室的Pecora和Carroll研究员发现混沌同步以后,混沌保密通信也迎来了研究热潮。混沌同步方法是其中重要的一个研究方向,目前对混沌同步的主要研究方法有:驱动-响应同步、主动-被动同步、单向耦合同步、相互耦合同步、脉冲同步、自适应同步、连续变量反馈同步、投影同步、函数投影同步、D-B同步等等[1～3]。其中,函数投影同步方法[4]更具有一般性和可行性,是近年来的研究热点,文献[1]在函数投影同步方法基础上对比例因子进行改进,提出函数矩阵比例因子,使两个系统的各个状态量以不同函数比例达到同步,即修正函数投影同步方法。文献[5]在已有基础上,基于单向耦合同步原理,直接通过驱动系统构造响应系统,并且只需在信道中传输一个驱动变量,实用性很强。而文献[6]在文献[5]的基础上加入自适应控制方法,加强了系统的鲁棒性,同时引入加速因子,改进了一般函数投影同步方案中同步时间与比例函数无关这一问题,提高了同步速度,有一定的实用价值。另外文献[7]研究了广义函数投影同步和参数调制的保密方案,把信息信号调制到驱动端参数中,在响应端已有控制器基础上增加自适应控制器,并且通过数值仿真成功达到同步并恢复出信息信号。但驱动端状态变量在信道中传输存在被破译的风险,文献[8]指出,依赖于参数或初始状态敏感性的方案容易被穷举攻击破译,基于相空间重构、回归映射等方法都可能破解一般的保密方案。

已有的混沌保密通信分为混沌数字通信和混沌模拟通信两类,其中混沌掩盖是混沌模拟通信最典型的方案[9],本文基于混沌掩盖提出一种新的同步方式——反馈调节函数投影同步,是指在发射端加入反馈调节,将信息信号与驱动端状态变量叠加后再反馈回驱动端,增强了信息信号的隐藏性和载波的不可识别性,同时利用修正函数投影同步,使驱动端、响应端达到同步,并解调出信息信号,最后通过Matlab仿真验证方案效果。

2 反馈调节函数投影同步方案描述

考虑驱动系统和响应系统如下:

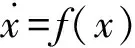
(1)

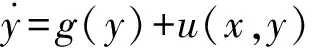
(2)

其中x,y∈Rn为驱动系统和响应系统的状态变量,f,g:Rn→Rn是连续可微的非线性函数,当f=g时为同结构混沌系统同步,f≠g时为异结构混沌系统同步,u(x,y)为非线性同步控制器。同步误差定义为

e=x-M(t)y

(3)

其中M(t)=diag[m1(t),m2(t),m3(t)],且对于∀t,mi(t)≠0。对于驱动端(1)和响应端(2),对于任意初值,若存在函数矩阵M(t)=diag[m1(t),m2(t),m3(t)]使得同步误差满足

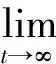
(4)

则称驱动系统和响应系统达到函数投影同步[10]。在系统(1)(2)的基础上做如下改进,选取某一状态变量叠加需传递信息信号后反馈回系统:

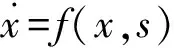
(5)

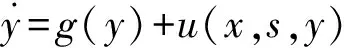
(6)

其中s=xi+i0,xi为驱动系统中选取的一个状态变量,i0为需传递的信息信号。同步误差定义同(3),当存在函数矩阵M(t)=diag[m1(t),m2(t),m3(t)]使得同步误差满足式(4)时,则称驱动系统和响应系统达到反馈控制函数投影同步。

以简化Lorenz方程为例,其动力学方程如下[11]:

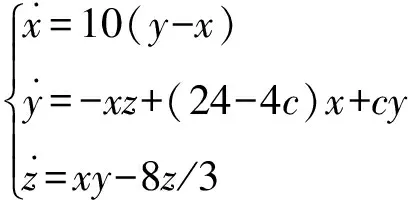
(7)

当c∈[-1.59,7.75]时,系统处于混沌状态。其混沌吸引子相图如图1所示。

用此系统构建驱动端和响应端动力学方程,并且将状态变量x1与需传递的信息信号叠加,并反馈回驱动端,响应端由函数投影同步控制器模块控制:

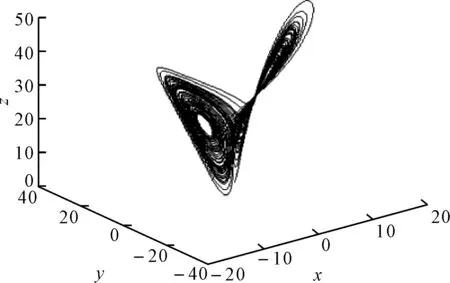
图1 简化Lorenz系统吸引子相图(c=-1)

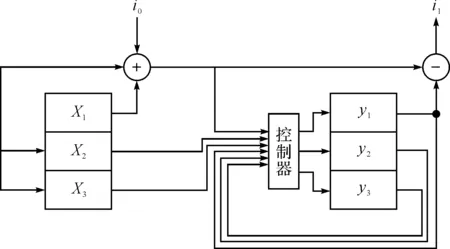
图2 系统逻辑框图

其中,i0为信息信号,s为载波信号,i1为解调信号,ui为控制器,由式(5)～(6),可设驱动端和响应端动力学方程分别为

(8)

(9)

定理1 当取控制器方程为

(10)

且c∈[-1.59,0]时,驱动端、响应端达到函数投影同步。

证明:由式(3)、(8)、(9),对误差方程分别求导,得:

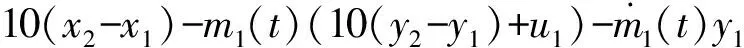
(11)

=(24-4c)s-sx3+cx2-m2(t)[(24-4c)y1

-y1y3+cy2+u2]

=(24-4c)(s-m2(t)y1)+m2(t)y1y3

(12)

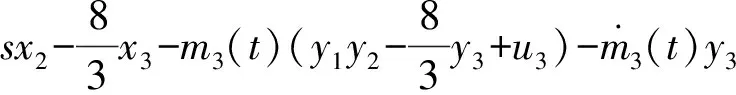
(13)

代入控制器方程(10),得:

(14)

设lyapunov函数为

(15)

则有

(16)

代入式(14)得

(17)

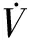
由Lyapunov稳定性定理可知,驱动端、响应端达到同步,得证。

3 数值仿真

取分岔参数c=-1,驱动端初始状态状态X=[1,2,3]T,响应段初始状态Y=[4,5,6]T,函数矩阵M(t)=diag[m1(t),m2(t),m3(t)],其中

(18)

在Matlab中进行数值仿真,仿真结果见图3～图8。

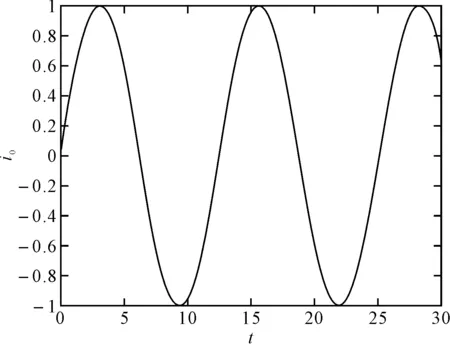
图3 信息信号

图4 恢复信号

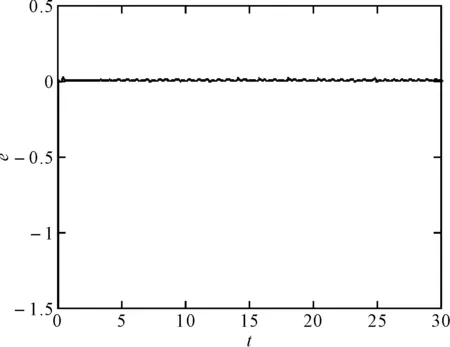
图5 信号误差

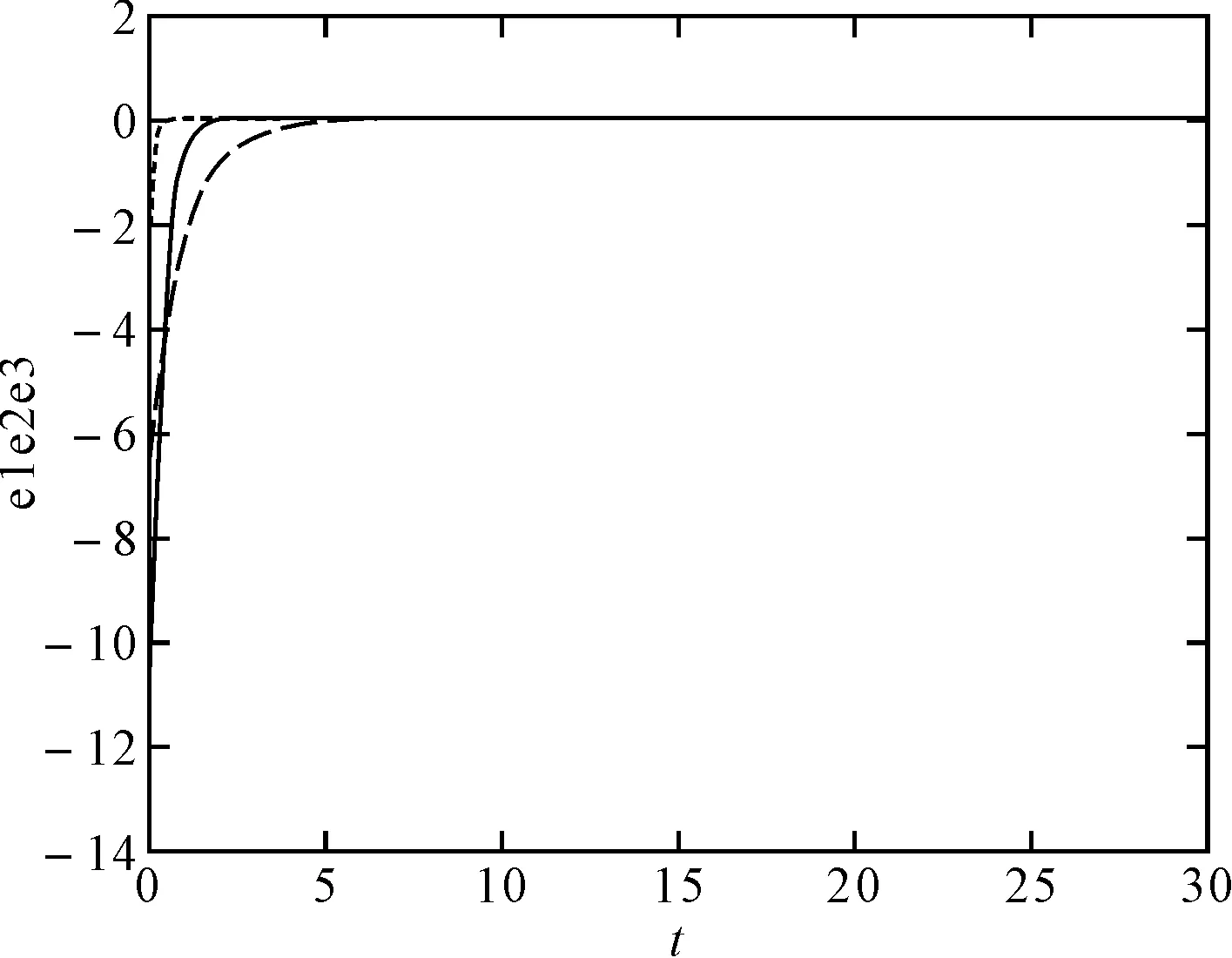
图6 系统状态量误差

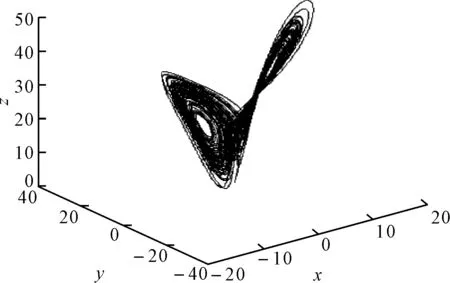
图7 驱动端吸引子相图

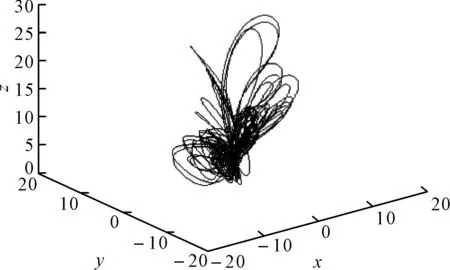
图8 响应端吸引子相图

图3、图4表明信息信号得到有效恢复,其信号恢复误差见图5,在短暂的窗口时间后信号恢复误差即趋于0,图6为驱动响应系统三个状态量的误差曲线,驱动端响应端很快达到了同步,但两系统的三个状态变量达到同步的速度有较大差异,最快达到同步的x1与y1在t=1s时已经达到同步,而x3与y3同步速度最慢,约t=5s时达到同步。图7为驱动端吸引子相图,相比图1可见信息信号完全隐藏在了系统中,图8为响应端吸引子相图,其根据函数比例关系进行了复杂的折叠变化,增强了保密性。

4 结语

本文介绍了反馈控制函数投影同步的原理和方法,通过构造合适的控制器,实现了驱动、响应系统的反馈调节函数投影同步,数值仿真验证了理论分析和计算的正确性,所采用方法适用于混沌保密通信,能够较好的掩盖信息信号,解决了信息信号“浮在”载波信号上面的问题,响应端信号也具有较为复杂的吸引子形态,抗破译性能较强,有一定的实用性。

同时,从图6中可见系统的不同状态变量达到同步的速度不同,在实际应用中,选用哪一维状态变量作为载波叠加信息信号并反馈回驱动系统,其同步速度和信号传递误差如何是下一步系统仿真可以研究的方向和问题。另外传输信号为音频等信号时对这一问题又是否存在较大影响,也可以作为下一步的研究方向。

[1] 杜洪越,曾庆双,王常虹,等.不同混沌系统的改进函数投影同步一般方法[J].系统仿真学报,2011,23(3):558-561. DU Hongyue, ZENG Qingshuang, WANG Changhong, et al. General Method for Modified Function Projective Synchronization in Different Chaotic Systems[J]. Journal of System Simulation,2011,23(3):558-561.

[2] 张莉,安新磊,张建刚.一种完全错乱广义投影同步的新方法[J].河北师范大学学报(自然科学版),2012,36(5):461-466. ZHANG Li, AN Xinlei, ZHANG Jiangang. On a New Method for Complete Dislocated General Hybrid Projective Synchronization[J]. Journal of Hebei Normal University,2012,36(5):461-466.

[3] Mohamed f. hassan. A New Approach for Secure Communication Using Constrained Hyperchaotic Systems[J]. Applied Mathematics and Computation,2014,246:711-730.

[4] Du H, Zeng Q, Wang C. Function Projective Synchronization of Different Chaotic Systems with Uncertain Parameters[J]. Physics Letters a,2008,372(33):5402-5410.

[5] 李建芬,李农.一类混沌系统的修正函数投影同步[J].物理学报,2011,60(8):93-99. LI Jianfen, LI Nong. Modified Function Projective Synchronization of a Class of Chaotic Systems[J]. Acta Physica Sinica,2011,60(8):93-99.

[6] 邓玮,方洁,吴振军,等.含有不确定项的混沌系统自适应修正函数投影同步[J].物理学报,2012,61(14):62-69. DENG Wei, FANG Jie, WU Zhenjun, et al. Adaptive Modified Function Projective Synchronization of a class of Chaotic Systems with Uncertainties[J]. Acta Physica Sinica,2012,61(14):62-69.

[7] 方洁,张昭晗,邓玮.基于广义函数投影同步的混沌保密通信研究[J].计算机仿真,2012,29(7):180-183,190. FANG Jie, ZHANG Zhaohan, DENG Wei. Chaos Secure Communication Research Based on Generalized Function Projective Synchronization[J]. Computer Simulation,2012,29(7):180-183,190.

[8] 翁贻方,翁莉娟,张蕾.提高混沌同步保密通信安全性的设计方案研究[J].电子与信息学报,2004,26(7):51-57. WENG Yifang, WENG Lijuan, ZHANG Lei. Research on Chaotic Synchronized Secure Communication Schemes to Improve Security[J]. Journal of Electronics & Information Technology,2004,26(7):51-57.

[9] 崔力,欧青立,张红强,等.混沌保密通信技术发展研究[J].通信技术,2010,43(5):129-131. CUI Li, OU Qingli, ZHANG Hongqiang, et al. Study on Chaotic Secure Communication Development[J]. Communications Technology,2010,43(5):129-131.

[10] 李睿,张广军,朱涛,等.不同阶混沌系统广义混合错位函数投影同步及在保密通信中的应用[J].计算机应用,2014,34(7):1915-1918,1959. LI Rui, ZHANG Guangjun, ZHU Tao, et al. Generalized Hybrid Dislocated Function Projective Synchronization Between Different-order Chaotic Systems and its Application to Secure Communication.

[11] Sun K, Sprott J C. Dynamics of a Simplified Lorenz System[J]. International Journal of Bifurcation and Chaos,2009,19(4):1357-1366.

Chaos Secure Communication Research Based on Feedback Regulating Function Projective Synchronization

CHEN Jingbo FENG Ping TANG Hong CHEN Jierui

(Department of Machinery & Electrical Engineering, Logistic Engineering University of PLA, Chongqing 401311)

In order to improve the security of chaos secure communication, based on the Lyapunov stability theory, a feedback regulating function projective synchronization method is proposed in this paper. This method is successfully applied to a chaos masking communication scheme. The mathematical deduction and simulation verifies its feasibility and validity.

chaos secure communication, feedback regulating function projective synchronization, chaos masking

2016年7月4日,

2016年8月24日

陈镜伯,男,硕士研究生,研究方向:电工理论与新技术。

TP273

10.3969/j.issn.1672-9722.2017.01.005