短波高速数传中的低复杂度Turbo均衡*
2017-02-09蒋超越李丽华金牡丹窦高奇
蒋超越 李丽华 金牡丹 窦高奇
(1.海军工程大学电子工程学院 武汉 430033)(2.东海舰队装备部 宁波 315122)
短波高速数传中的低复杂度Turbo均衡*
蒋超越1李丽华1金牡丹2窦高奇1
(1.海军工程大学电子工程学院 武汉 430033)(2.东海舰队装备部 宁波 315122)
为了消除短波信道中的码间串扰,提出了Turbo均衡方式。传统的Turbo均衡计算复杂,不利于实现。论文列举了几种低复杂度的Turbo均衡方式,并且对其结构、均衡效果、计算复杂度做了对比分析,得出SFIC均衡方式消除因短波多径效应引起的码间串扰效果最好。
Turbo均衡; 低复杂度; SFIC
Class Number TP301
1 引言
短波通信是一种重要的无线通信方式,广泛应用于军事、气象、海事等领域。短波区别于其它无线通信方式的一个重要特点是短波在空中传播时可经过电离层反射,无需中继设备,因此抗损毁能力强,在军事上具有重要的作用。现代战争已经进入信息化时代,制信息权越来重要,因此需要短波通信具有更高的传输速率,更稳定的传输质量。而由于电离层易受季节、昼夜和太阳活动等影响,所以短波传输信道是随参信道,使得短波通信的稳定性、可靠性不是很理想。其中影响最严重的是多径效应,它会造成频率选择性衰落。因此,短波数据在传输过程中会存在严重码间串扰(ISI)。如何消除码间串扰也成为提高短波传输速率的关键。均衡技术是消除码间串扰的主要方式,Turbo均衡是一种有效的均衡方式,它的提出为短波均衡技术的发展提供了新的研究方向。
Turbo均衡主要有基于网格图的均衡和基于滤波器的均衡两大类,基于网格图的均衡通常计算较为复杂,不利于实际应用,因此在实际情况中需要降低其复杂度。而通常基于滤波器的均衡计算复杂度比较低,易于实现。下文主要介绍基于滤波器的均衡—LMMSE和SFIC。在LMMSE基础上做了两种极端情况的假设,得到LE(Ⅰ)和LE(Ⅱ)。对于SFIC,将其滤波器系数改为时变系数得到SFE,并把它与LE(Ⅰ)结合起来得到HSFC。
2 Turbo均衡
2.1 Turbo均衡基本结构模型
图1中符号上标D和E分别代表译码器和均衡器,下标a和e分别代表先验信息和外信息。

图1 Turbo均衡基本结构框图

2.2 低复杂度Turbo均衡
在所有的Turbo均衡算法中,基于网格的MAP算法[2]效果是最佳的。MAP算法将计算每个比特的后验概率P(cn,j|r),后验LLR的计算考虑了所有接收符号和先验信息的影响,并在网格图上正、反向搜寻所有可能的路径,它使每个发送比特发生错误的概率最小。但是MAP均衡有一个很大的缺点制约着它的发展,它的计算复杂度与调制进制数和信道记忆成指数增长,所以只能适用于低阶调制和短弥散信道。而如何降低计算复杂度成为Turbo均衡研究的一个重要内容。
对于传统的均衡方式,大致可以分为三类[3]。第一类是线性均衡器(LE),其系数可调;第二类是判决反馈均衡器(DFE),利用已检测符号来抵消当前被检测符号中ISI;第三类是最大似然序列估计均衡器(MLSE)[4],其均衡时遵循最大似然准则。在此基础上将Turbo均衡迭代处理的思想引入其中,在保持较好效果的同时降低计算的复杂度。
下文给出了两种低复杂度的Turbo均衡方式,它们将传统的均衡器改造成可以利用译码反馈软信息的SISO均衡器,达到降低计算复杂度同时保持较好的性能的目的。为了进一步降低计算复杂度在这两种方式的基础上又做了改进。
3 低复杂度LMMSE均衡器
LMMSE均衡是在第一类均衡方式的基础上采用线性滤波器代替MAP符号检测。LMMSE均衡器包含了一个长度为N=N1+N2+1的时变FIR滤波器。结构如图2所示。

图2 LMMSE结构框图
在单个数据块传播过程中,认为信道条件变化不大,即信道的冲击响应不变。则信道的卷积矩阵为
发送的符号序列为
xn=[xn-N2-L+1,xn-N2-L+2,…,xn+N1]T
接收序列为
Γn=[rn-N2,rn-N2+1,…,rn+N1]T
噪声为
ηn=[ηn-N2,ηn-N2+1,…,ηn+N1]T
Vn=Cov(xn,xn)=diag[vn-N2-L+1,…,vn+N1]
s=H[01×N2+L-1,1,01×N1]T
IN为N阶单位矩阵。

均值和方差为
可得:
则均衡器输出的外信息为
通过以上计算可以看出,均值和方差都是时变的,因此线性滤波器的的系数也是时变的。在处理完当前符号后都要对滤波器的系数进行更新,系数的更新是逐符号的,计算复杂度很大。为了减少计算量,将用固定的滤波器系数代替时变系数[7],认为在一个数据块内系数是不变的。可将LMMSE做两种极端情况的假设,LE(Ⅰ)和LE(Ⅱ)。

均值为
在方差的计算过程中,采用时间评均的方法求解。可以简化为

4 低复杂度软反馈干扰抵消(SFIC)均衡器
SFIC在第二类均衡方式基础上,引入译码反馈软信息,通过联合均衡和译码来提高性能[8]。不仅能像传统DFE[9]一样消除后尾干扰,还能消除前导干扰。SFIC在估计反馈序列时,考虑译码器反馈的全信息和均衡器输出信息。克服了外信息不足的影响,避免判决错误的扩散。结构如图3所示。

图3 SFIC结构框图
SFIC由三个FIR滤波器组成:f,b1,b2。定义系数矢量为
b1和b2分别用于消除前导ISI干扰和后尾ISI干扰。均衡器的输出为

k∈[-(L1+L2),…,-1,1,…,(L1+L2)]
Eh为信道能量,通常归一化为1。
对于BPSK调制方式,忽略偏移因子μ,利用译码器反馈的全部信息来提高对发送符号的估计。
可得:

经过改进得到的SFIC的计算复杂度随信道的记忆长度成线性增长,但是其前馈滤波器系数是时不变的,与先验信息无关。SFE是一种结构与SFIC相似的均衡器[10],区别在于SFE的前馈和反馈滤波器系数是时变的,受先验信息影响。HSFE是以SFE为基础,结合LE(Ⅰ)的一种混合均衡方式。在初始迭代时采用LE(Ⅰ),克服先验信息不足的影响。随着迭代的进行,改用SFE,则可以避免固定系数对噪声放大带来的不良影响。
5 低复杂度均衡器比较
5.1 均衡器结构对性能影响的比较

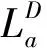
5.2 误码率性能比较
在BPSK调制方式下使用递归系统卷积码(RSC),码率R=1/2。数据按帧发送,每帧包括2052个编码比特,假定信道在一帧内是恒定不变的。仿真信道采用Proakis C信道,该信道会产生严重的码间串扰[3]。根据文献[3,5,7~8]仿真结果如图4所示。

图4 不同Turbo均衡算法的误码性能曲线
从图4可以看出,无论是在低信噪比还是高信噪比情况下,LMMSE均衡方式的误码率都低于其它算法。其系数是时变的,可以根据信道的变化及时调整,保证了在信噪比较低时也能保持较好的均衡效果。但是因为系数的调整是逐个符号进行的,所以计算量非常的大,因此实用性不佳。在此基础上使用固定系数代替时变系数,即LE(Ⅰ)(图中LE(1))LE(Ⅱ)(图中LE(11))和,使得计算量降低。同时在初始迭代过程中,由于外信息的缺乏,使用译码反馈信息反而会导致均衡器效果不佳,造成错误判决的扩散。因此LE(Ⅰ)在低信噪比时效果很好。随着迭代的继续,外信息会越来越丰富,固定的滤波器系数在提高信噪比的同时也放大了噪声,LE(Ⅰ)在信噪比6dB~10dB阶段时,误码率下降缓慢,没有明显的瀑布区。当信噪比高于10dB时,误码率曲线的下降趋势比以前更差。对于LE(Ⅱ),由于采用了完美先验信息的假设,使得在低信噪比时估计序列与实际发送序列相差较大,因此在低信噪比条件下误码率曲线下降缓慢。只有在信噪比大于10dB的条件下,此时高信噪比更能克服传播过程的干扰,估计序列更加接近发送序列,使得误码率曲线出现陡降的瀑布区。传统的DFE在初始判决时由于外信息的缺乏会造成错误判决的扩散,SFIC由于采用了时不变滤波器,所以在低信噪比阶段能取得几乎与LE(Ⅰ)一样的效果。SFIC中的两个反馈滤波器接收译码器反馈的全信息用于消除前导干扰和后尾干扰,克服了外信息不足的影响。随着迭代的继续,当信噪比大于6dB以后,SFIC也能保持较好的性能,误码率曲线出现瀑布区。HSFE在信噪比低的时候效果不佳,随着信噪比的增加其性能会逐渐改善,但是比SFIC要差。
5.3 计算复杂度对比

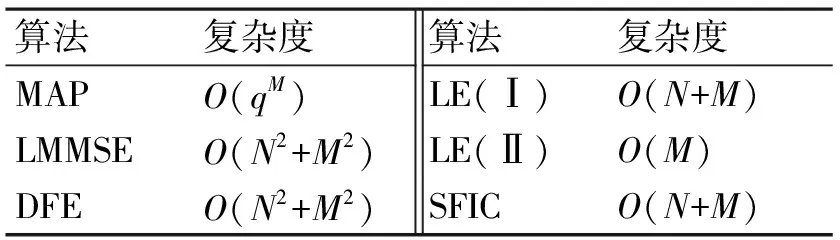
表1 计算复杂度对比
5.4 结论
通过以上分析可以得出以下结论:
1) 就整体效果来说,无论在信噪比高低,LMMSE的误码率曲线最接近无ISI情况下的误码率曲线,但是它的计算也最为复杂。
2) LE(Ⅱ)只有在高信噪比条件下才能使误码率瀑布区,计算复杂度小。
3) 对于两种改进的低复杂度均衡方式LE(Ⅰ)和SFIC,两者在计算复杂度上一致。
在低信噪比条件下,两者对于误码率的降低几乎一致,当信噪比进一步升高,LE(Ⅰ)的降低误码率的效果比SFIC差。SFIC误码率曲线会出现瀑布区,而LE(Ⅰ)则相对平缓。在高信噪比的条件下,LE(Ⅰ)降低误码率的效果比以前更差。因此对于在Proakis C信道中,运用BPSK调制方式下,推荐使用SFIC均衡方式。
6 结语
在短波传输中,码间串扰是制约传输速率提高的关键因素,Turbo均衡是一种效果很好的消除码间串扰的方式。Turbo均衡有一个显著的缺点就是计算复杂,本文针对这个问题,分析比较了多种低复杂度的均衡方式,并得出在对Watterson信道模型简化的Proakis C信道中SFIC均衡方式解决码间串扰的性能更佳。
同时需要指出本文在算法分析中是假设信道冲击响应已知并在一个数据块内不变的。而实际短波信道是时变的,并且信道估计也会有误差。所以下一步可以研究通过更加精确的信道估计提高性能。
[1] Douillard C, Jezequel M, Berrou C, et al. Iterative correction of intersymbol interference: Turbo equalization[J]. Eur. Trans. Telecommun.,1995.6(5):507-511.
[2] Bahl L R, Cocke J, Jelinek F, et al. Optimal decoding of linear codes for minimizing symbol error rate[J]. IEEE Trans. Inf. Theory,1974,IT-32:284-287.
[3] Proakis J G. Digital communications[M]. 4th edition. New York: McGraw-Hill,2001.
[4] Forney G D. Maximum likelihood sequence estimation of digital sequences in the presence of intersymbol interference[J]. IEEE Trans. Inform. Theory,1972,IT-18:363-378.
[5] Tüchler M, Singer A C, Koetter R. Minimum mean squared error equalization using a-priori information[J]. IEEE Trans. on Signal Processing,2002,50(3):673-683.
[6] Haykin S. Adaptive filter theory[M].北京:电子工业出版社,2006. Haykin S. Adaptive filter theory[M]. Beijing: Publishing House of Electronics Industruy,2006.
[7] Tüchler M, Koetter R, Singer A C. Turbo equalization: Principles and new results[J]. IEEE Trans. Commun.,2002,50(5):754-767.
[8] Laot C, Bidan R L, Leroux D. Low-complexity MMSE Turbo equalization: a possible solution for EDGE[J]. IEEE Trans. Wireless Commun.,2005,4(3):965-974.
[9] Austin M E. Decision feedback equalization for digital communication over dispersive Channels[R]. MIT Lincoln Laboratory,1967.
[10] Lopes R R, Barry J R. The soft-feedback equalizer for Turbo equalization of highly dispersive channels[J]. IEEE Trans. Commun.,2006,54(5):783-788.
Low Complexity Turbo Equalization in HF High Speed Data Transmission
JIANG Chaoyue1LI Lihua1JIN Mudan2DOU Gaoqi1
(1. College of Electronic Engineering, Naval University of Engineering, Wuhan 430033) (2. Equipment Department, East China Sea Fleet, Ningbo 315122)
In order to eliminate ISI in HF channel, the Turbo Equalization is proposed. The traditional Turbo Equalizer has high computational complexity and is not conducive to realize. This artcle lists kinds of low complexity Turbo equalizers, and compares and analyzes from architecture, equalization effect and computational complexity. The result shows the Turbo equalization based on SFIC has a good effect to eliminate ISI.
Turbo equalization, low complexity, SFIC
2016年7月11日,
2016年8月27日
海军工程大学自然科学基金(编号:HGDQNJJ15017)资助。
蒋超越,男,研究方向,通信工程。李丽华,女,硕士,讲师,研究方向,无线通信工程。金牡丹,女,硕士研究生,高级工程师,研究方向:通信。窦高奇,男,博士,副教授,研究方向:无线通信工程。
TP301
10.3969/j.issn.1672-9722.2017.01.010
