风对直升机航路规划的影响分析*

陈贻焕 陈佳琪 郑 强

(海军航空工程学院 烟台 264001)



风对直升机航路规划的影响分析*

陈贻焕 陈佳琪 郑 强

(海军航空工程学院 烟台 264001)

针对风对直升机航程的影响,根据飞行气象学中风对飞行的影响描述以及实际需求,建立了直升机在空中待命状态时飞往预定点的航迹模型。在此基础上,仿真分析了风速和风向、航速和航向对直升机飞行时间的影响。仿真结果表明风对直升机航路规划的影响需要依据模型进行定量分析。为直升机航路的优化,作战效能的提高提供了决策依据。

航路规划; 风; 飞行时间; 直升机

Class Number TB391.9

1 引言

直升机航路规划是指在给定的空间区域内,在满足最小转弯半径的约束条件下,反潜直升机从某个初始位置出发,在最短时间内抵达预定点的最优或可行轨迹[1～2]。所谓预定点,一般是指有一定战术意义的位置点,如基准点、搜索中心、回合点等。在这些过程中,直升机航路规划一般不需要利用地形和敌情威胁等信息,而主要考虑风的变化和分布对飞行时间的影响,以便在预定的时间内到达指定区域执行任务。由于风的复杂性,相关的文献中只是针对风向对航程的影响进行了定性的描述[3～5],并没有建立风场的仿真模型,特别是没有考虑风对直升机机动(如转弯)的影响。风切变模型过于复杂[6～7],对于较大范围的空域来说,可以忽略风切变的影响。本文在飞行气象学中风对飞行的影响描述及实际任务的基础之上,建立风影响下直升机的航迹模型,并分析直升机航速和航向及风速和风向的变化对飞行时间的影响,为直升机的航路规划提供了定量决策依据。

2 航路建模

风对直升机飞行的影响可用航行速度三角形[8～10]来描述,它准确反映了风对直升机航行影响的基本规律。以x轴为正东方向,y轴为正北方向,建立平面直角坐标系,如图1所示。

图1 航行速度三角形

图1中,V1为直升机的航速(空速),V1_A为空速方向;V2为风速,V2_A为风速方向(去向);V0为地速,V0_A为地速方向;δ0为偏流角,即地速矢量和空速矢量之间的夹角,地速方向逆时针旋转到空速方向,则为正,反之为负。文中速度单位为km/h,角度单位为rad。

在领航学中,所有角度都是以地理上的正北为基准,顺时针转为正,反之为负,为建模方便,把V1_A、V2_A和V0_A分别转换成x轴逆时针旋转到航向和风的去向的角度α0、φ和γ0,具体转换过程为:

同理把V2_A、V0_A转换成φ、γ0。

由余弦定理有

(1)

由正弦定理有

(2)

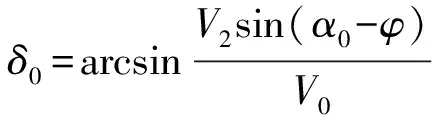
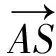
(3)

所在区域重力加速度为g,直升机的最大转弯坡度为ω,则直升机的最小转弯半径为R=V12/(gtanω)。

假设0≤θ≤π/2,其他情况与此类似。

1) 当θ≤γ0<π+θ时,直升机从初始位置A顺时针飞往预定点S的航迹如图2所示。

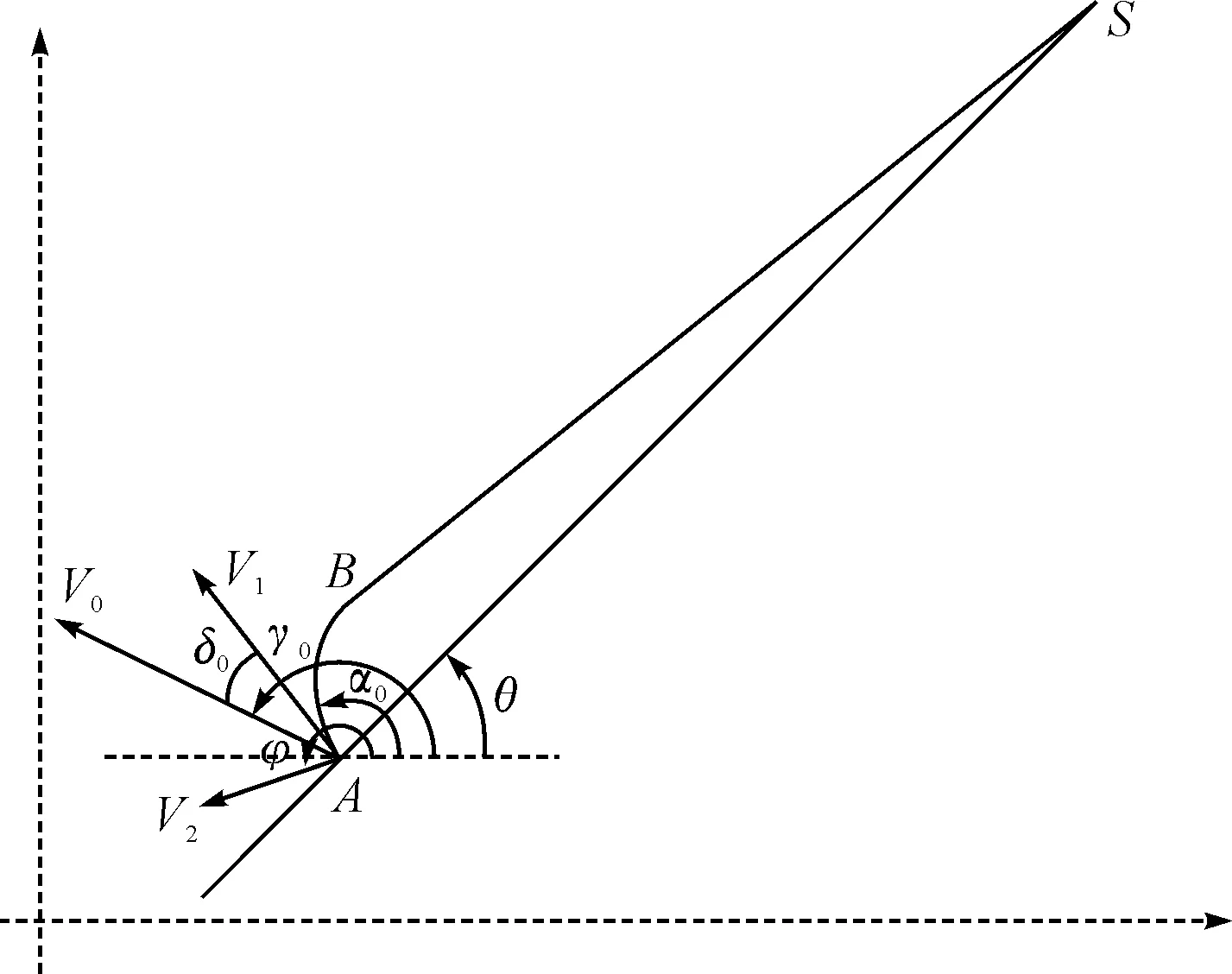
图2 顺时针航迹图

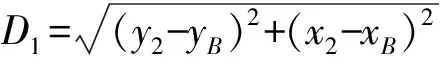
模型如下:

当0≤t≤T0时,

(4)

其中(xt,yt)为t时刻直升机的坐标,αt为t时刻的航向,αt=α0-V1t/R,有

(5)

到达B点时,

(6)

(7)

(8)

(9)

联立式(6)～(9)可解出T0。

当T0

(10)

2) 当π+θ≤γ0<2π或0≤γ0<θ时,直升机从初始位置A逆时针飞往预定点S的航迹如图3所示。

图3 逆时针航迹图

因为航向角最大为2π,所以

(11)

当0≤t≤T0时,

(12)

到达B点时,

(13)

(14)

与αt相同,γB也不能超过2π,有

(15)

联立式(13)～(15)和(9)可解出T0。

当T0

3 仿真结果分析

3.1 航路模型仿真

仿真条件:飞机的初始位置为A(10,20),航速200km/h,航向分别为0°、100°、200°和300°;预定点的位置为S(20,30);风速50km/h,风向200°。仿真结果如图4所示。

图4 航路模型仿真结果

由图4可以看出:仿真结果验证了模型的正确性。

3.2 风速、风向对飞行时间的影响

仿真条件:直升机初始位置为A(20,20),航速200km/h,航向20°;预定点的位置为S(30,30);风向从0到360°,风速从0到50km/h。仿真结果如图5所示。

图5 风速、风向对飞行时间的影响

图5表明:风向与风速共同对飞行时间起作用。当风向与目标方位(45°)的夹角小于90°时,风速的增大以及夹角的减小都可以减少飞行时间,且当风向与目标方位相同时,飞行时间最短;当风向与目标方位的夹角大于90°时,风速和夹角的增大都会增加飞行时间;当风向与目标方位相同时,仅考虑风速对飞行时间的影响,时间差也可以达到2.26分钟。

例如,在5级风(风速约30km/h)、风向90°的条件下,飞行时间约为3.86分钟,若忽略风的影响,飞行时间约为4.23分钟,误差近10%。可见,风对直升机的航路规划具有重要的影响。

3.3 航速、航向变化对飞行时间的影响

1) 仿真条件:直升机的初始位置为A(20,20),预定点的位置为S(30,30);风速20km/h,风向为0°;航向从0到360°,航速从100km/h到200km/h。仿真结果如图6所示。

图6 航速、航向对飞行时间的影响

图6表明,航向接近目标方位反方向时,飞行时间逐渐增加;航向接近目标方位同方向时,飞行时间逐渐减少;不管航向如何,随着航速的增大,飞行时间逐渐减少。

2) 仿真条件:直升机的初始位置为A(20,20),预定点的位置为S(30,30);风速20km/h,航向为20°;风向从0到360°,航速从100km/h到200km/h。仿真结果如图7所示。

图7 航速、风向对飞行时间的影响

图7表明,不管风向如何,随着航速的增大,飞行时间逐渐减少;风向与目标方位同向时,飞行时间最短;风向与目标方位反向时,飞行时间最长。

3) 仿真条件:直升机的初始位置为A(20,20),预定点的位置为S(30,30);风速20km/h,航速为200km/h;风向从0到360°,航向从0到360°。仿真结果如图8所示。

图8表明,风向与航向相同,且接近目标方位反方向时,飞行时间逐渐增加,当航向与风向相同,且与目标方位相反时,飞行时间最长;航向与风向相同,且靠近目标方位相同方向时,飞行时间逐渐减少,当航向与风向相同,且与目标方位相同时,飞行时间最短。

4 结语

实际飞行中,风对直升机飞行时间的影响不能忽略。尤其是当海况较差时,风速有时可达空速的0.2倍,这时风会严重影响到对飞行时间的估算,此时需要运用风场模型对飞行时间进行计算,以便更好的实现直升机航路规划。仿真结果可以很直观表示出风场模型各个变量对飞行时间的影响,此模型能够很好地满足直升机仿真训练的需求。

[1] 闵昌万,袁建平.军用飞行器航迹规划综述[J].飞行力学,1998,16(4):14-19. MIN Changwan, YUAN Jianping. Introduction of Military Aircraft Route Planning[J]. Flight Dynamics,1998,16(4):14-19.

[2] 杜萍,杨春.飞行器航迹规划算法综述[J].飞行力学,2005,23(2):10-13. DU Ping, YANG Chun. Introduction of Air Vehicle Path Planning Algorithms[J]. Flight Dynamics,2005,23(2):10-13.

[3] 李新胜,杜冬,李根军,等.高空风对飞行的影响在雷达模拟机中的建模和实现[J].中国民航飞行学院学报,2004,15(2):28-31. LI Xinsheng, DU Dong, LI Genjun, et al. Modeling and Realization of Influences on Flight by Upper Wind in Radar Simulator[J]. Journal of Civil Aviation Flight University of China,2004,15(2):28-31.

[4] 曾勇.风影响下的航迹修正[J].中国民航飞行学院学报,2003,14(1):26-27. ZENG Yong. Track Correction on the Influence by Wind[J]. Journal of Flying College Caac,2003,14(1):26-27.

[5] 李春生.浅谈风对航空飞行的影响[J].中国民航飞行学院学报,2001,14(1):45-46. LI Chunsheng. The Influence of Wind to Aviation Flight[J]. Air Traffic Management,2001,14(1):45-46.

[6] 郭卫刚,徐彦军,边若鹏.风切变对飞机平飞特性的影响分析[J].飞机设计,2008,28(3):1-3. GUO Weigang, XU Yanjun, BIAN Ruopeng. Analysis on Influence of Aircraft Performance by Wind Shear[J]. Aircraft Design,2008,28(3):1-3.

[7] 方振平,李慧波.减少飞机对风切变敏感性的研究[J].航空学报,1992,13(6):249-250. FANG Zhenping, LI Huibo. A Study on Reduction of Aircraft Sensitivity to Wind Shear[J]. Acta Aeronautica ET Astronautica Sinica,1992,13(6):249-250.

[8] 方振平.飞机飞行动力学[M].北京:北京航空航天大学出版社,2005:122-123. FANG Zhenping. Aircraft Flight Dynamics[M]. Beijing: Beihang University Press,2005:122-123.

[9] 章澄昌.飞行气象学[M].北京:气象出版社,2000:57-59. ZHANG Chengchang. Flight Meteorology[M]. Beijing: China Meteorological Press,2000:57-59.

[10] 张军.军事气象学[M].北京:气象出版社,2005:94-96. ZHANG Jun. Military Meteorology[M]. Beijing: China Meteorological Press,2005:94-96.

Analysis on Influence of Helicopter Route Planning by Wind

CHEN Yihuan CHEN Jiaqi ZHENG Qiang

(Naval Aeronautical Engineering Academy, Yantai 264001)

Aimed at the influence by wind on the helicopter route, according to the description about influence on flight by wind in the flight meteorology and the concrete demand, the route model of the helicopter in air on-call situation flying towards the scheduled point was established. On the basis of the model, changes of the wind speed and the wind direction, the helicopter speed and the helicopter direction to the influence of the flight time were analyzed in the simulation. The simulation results showed that the influence by wind on the route planning cannot be neglected, and should be quantitatively analyzed. These provide the policy decision basis for optimization of route planning, improvement of combat efficacy of helicopter.

route planning, wind, flight time, helicopter

2016年7月9日,

2016年8月17日

陈贻焕,男,硕士,高级工程师,研究方向:航空反潜。陈佳琪,女,硕士,讲师,研究方向:航空反潜。郑强,男,博士研究生,研究方向:航空反潜。

TB391.9

10.3969/j.issn.1672-9722.2017.01.014