宝马IntegralⅤ式后桥四轮定位调整的车间应对策略
2017-02-05杭州技师学院
杭州技师学院 李 琦,吴 静
宝马整体式后桥悬架Integral V是在Integral IV 后桥的基础上全新研发的后续产品。作为一种“立体”式独立悬挂,它是由前束控制臂、横向摆臂(上部)、梯形控制臂(下部摆臂)和连接导杆等组成。因其具有更好的车轮导向性能、最佳的安全性能,减噪、减振效果,可提高行驶动力性,可实现行驶动态管理及可实现后轮转向等优点,故在F01、F02、F18等车型上得到广泛应用。
由于Integral V后桥的结构特点,后桥车轮外倾角和前束的值呈正线性/负线性相关(图1),因此每次调整摆臂(下部横摆臂)或横向摆臂(上部横摆臂)上的调整螺钉时,都会引起车轮外倾角和前束的同时变化,故在实际调整中无法对前束或外倾进行单独调整。为此,宝马维修技术文件提供了一种方法——作图法协助维修技师进行调整。作图法对于很多维修技师来说,较难掌握或显得比较陌生,或限制于车间条件,或担心精度不够等原因不愿意事先作图,这导致很多维修技师在车间实际生产过程中,按常规方法对其进行四轮定位调整时,经常出现反复调整,而达不到预期的效果,费时费力,极大地影响了工作效率。
1 IntegralⅤ后桥四轮定位调整作图法介绍
根据宝马综合服务技术应用软件(ISTA)提供的5系F18车型的维修说明,可知,在图1中,D线为调整摆臂(下部横摆臂)上的螺栓时,外倾角B和前束A的值变化规律,C线为调整横向摆臂(上部横摆臂)上的螺栓时,外倾角B和前束A的值变化规律。点1为待调整车辆的四轮定位实际参数,点3为待调整车辆的四轮定位的目标参数(标准点),点2则为通过作图法而得到的调整中间值点。作图法的基本步骤如下。
(1)在车桥检测台上读取车轮外倾角和前束的实际值1 ,并记录到图表中,在本例中,车轮外倾角B=-100′、前束A=-15′,用坐标(-100′,-15′)表示。
(2) 通过记录的实际值1 ,画横向摆臂(上部横摆臂)直线C的平行直线, 在“摆臂”直线D上得到交点2,并读取出中间值点2的坐标=(-117′, -2′)。
在调整时,通过转动横向摆臂(上部横摆臂)的调整螺栓,将外倾角和前束由实际点1调整到中间值点2=(-117′, -2′)处;再通过转动摆臂(下部横摆臂)的调整螺栓,将外倾角和前束由中间值点2调整到标准点3,调整即结束。注意:若选择的中间点不同,上下臂的调整顺序也就不同,但方法一样,不再赘述。
2 建立模型,确定中间点区域
由于误差的存在,在实际的四轮定位调整中,一线维修技师一般是通过四轮定位仪把四轮定位调整参数调整在标准值允许的误差范围内即可。这也就允许技师在使用作图法调整时,中间值也有一定的误差范围,即为中间点区域。
2.1 建模假设
(1)外倾角/前束的变化规律为2条严格意义上的直线。其中调整摆臂(下部)时,遵循直线为D线,表述为DxB+DyA+Db=0,调整横向摆臂(上部)时,遵循直线为C线,表述为CxB+CyA+Cb=0。标准值坐标=(α ,β),外倾角允许误差Δα,前束允许误差Δβ,故带误差的标准值=(α±Δα,β±Δβ);实际值坐标=(γ ,δ)。
(2)在进行四轮定位调整时,遵循自上而下的顺序,即先调C线,再调D线。
2.2 建立模型
调整横向摆臂时,外倾角/前束值从实际点(γ ,δ)沿着C1:Cx(B-γ)+Cy(A-δ)=0变化,而过标准点(α ,β)D2:Dx(B-α)+Dy(A-β)=0。C1与D2相交即为所求的中间值。同理,可得到过标准值误差域上顶点(α-Δα,β+Δβ),下顶点(α+Δα,β-Δβ)的D1线:Dx(B-α+Δα)+Dy(A-β-Δβ)=0,D3线:Dx(B-α-Δα)+Dy(A-β+Δβ)=0。
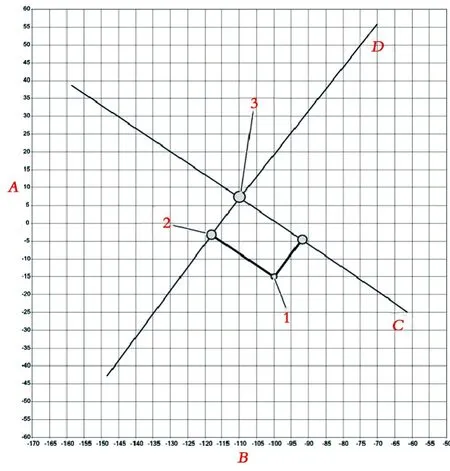
图1 车轮外倾角/前束调整相关性图(5系F18车型)
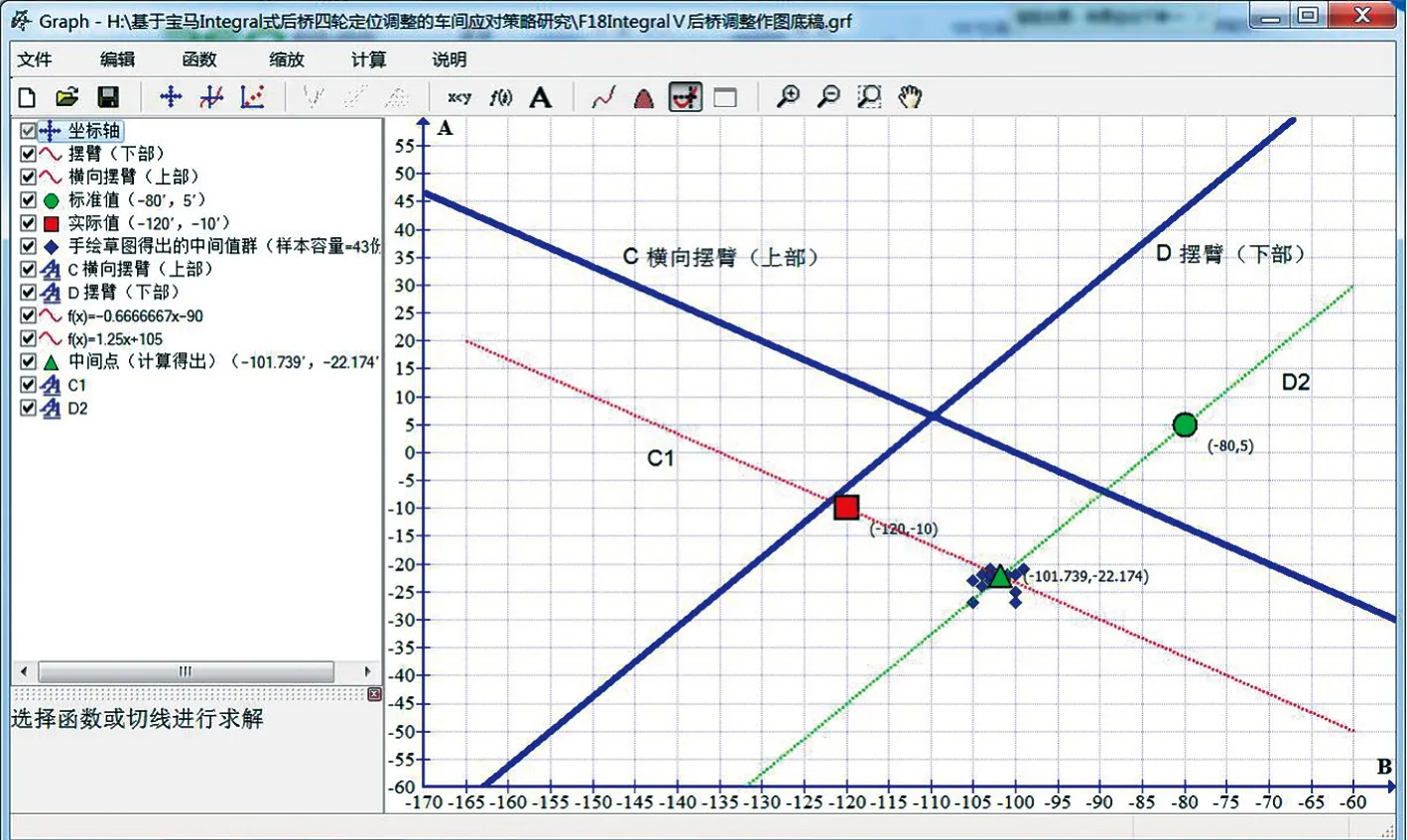
图3 徒手草绘中间点数列(截屏)
由D1、D3与C1分别相交,得到两点,介于此两点间的区域即可认为是可调中间值,在此两点之外的区域即为不可调中间值。
因此,维修技师在对Integral V整体式后桥进行四轮定位作图法调整时,一定要使调整过程中产生的瞬时中间值落在可调中间值域中,否则,将无法顺利完成四轮定位的调整,影响工作绩效。
如果需要改变调整顺序,即先调节D线,再调节C线,模型将有所变化,导致可调中间值域和不可调中间值域都与之不同。但建模的方法类似,在此亦不再赘述。
3 实例
现在以宝马F18为例,在四轮定位仪上读取到右后轮定位参数如下:标准点坐标=(α,β)=(-80′,5′),外倾角允许误差Δα=25′,前束允许误差Δβ=6′。实际值坐标=(γ,δ)=(-120′,-10′)。根据建立的数学模型,应用函数软件Graph得到的图表如图2所示。因外倾角允许误差较大,形成一个面积较大的水平方向的矩形,因本案例中采用“由上至下”的调节顺序,从实际值点作横向摆臂C的平行线,得到C1,因实际值不存在误差(或存在误差,但不可读),因此该直线C1具有唯一性。通过标准值域的2个顶点作摆臂D的平行线,得到D1与D3,此二线切割C1线,根据模型即可得“可调中间值域”,图2中的绿色线段。从此域中的任何一点,调节摆臂(下部),即可把四轮定位调整至“标准值误差域”中,完成调整。
然而在实际工作过程中,由于作图存在误差,主要表现为:所作线段不直;与C线,D线不平行;数据读取误差等。对此,通过试验发现,在给定实际点与标准点坐标后,试验者被要求不使用任何直尺工具,在最短时间内(要求最长不超过1 min时间),徒手草绘出中间点,并读取其坐标值。根据得到的实验数据(中间点数列)输入函数软件Graph中得到图表(图3)。
由图3可见,经过极短时间内草绘得到的中间点聚集包围在理论中间点处,且多有重叠。综合图2和图3可以肯定即使是徒手草绘得到的中间点既在可调中间值域内,且随着熟练程度,也无限接近理论中间点。然而,在实际调整过程中,外倾角与前束总是以坐标的形式(成对)沿着C1直线变化,理论中间值总是以一种隐形的方式呈现在四轮定位仪显示屏上。那么草图绘制得出的中间值就只是打开这个隐形数据的窗户,是维修技师调整的一个方向,其精度也就没有那么高的必要了。
4 总结
通过以上研究,发现在车间对Integral V式后桥调整时,维修技师需要的只是一张空白的图表(图1),一直铅笔而已,画出的中间点值只是作为调整的一个方向,其精度已经能很好地满足实际调整的需要。
以上实例中实际点与标准点间的连线与C线和D线都有较大的一个角度。通过作出中间点,先调整横向摆臂至中间值,再调整摆臂由中间值调整至标准值。
特殊情况时,当实际点与标准点的连线与C线的夹角非常小,甚至与C线平行时,无需找出中间点,可以直接通过调整横向摆臂调至标准值;当实际点与标准点的连线与D线的夹角非常小,甚至与D线平行时,则可以直接通过调整摆臂调至标准值。
以上可以看出,此策略探索可以大大提高Integral V式后桥四轮定位的工作绩效,避免盲目调整。
