高阶双组分Camasss-Holm系统解的Hölder连续性

王 彬，周寿明，宋雪珠



高阶双组分Camasss-Holm系统解的Hölder连续性

王 彬，周寿明*，宋雪珠

(重庆师范大学 数学科学学院，重庆 401331)

由于高阶双组分Camassa-Holm系统是局部适定的，故该系统的解是连续依赖于初值条件的﹒本文根据局部适定性的结果，利用索伯列夫不等式和能量估计方法，首先给出高阶双组分Camassa-Holm系统解的一个先验估计；然后依据先验估计和索伯列夫插值公式，推导得出高阶双组分Camassa-Holm系统的解是Hölder连续的﹒

高阶双组分Camassa-Holm系统；索伯列夫空间；Hölder连续

考虑如下高阶双组分Camassa-Holm系统

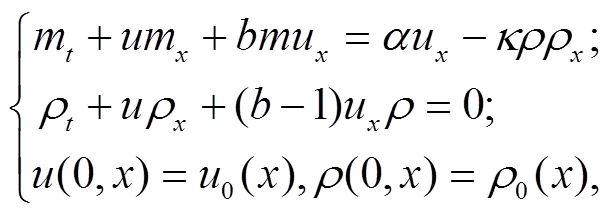
最近Escher和Lyons[1]提出了系统(1)，并给出了爆破准则．在Besov空间

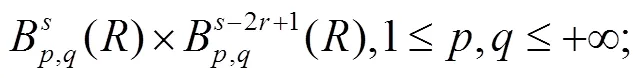
中，Chen和Zhou[2]依据运输方程理论和Littlewood-Paley分解理论得到了系统(1)的局部适定性．更进一步，He和Yin[3]在Besov空间

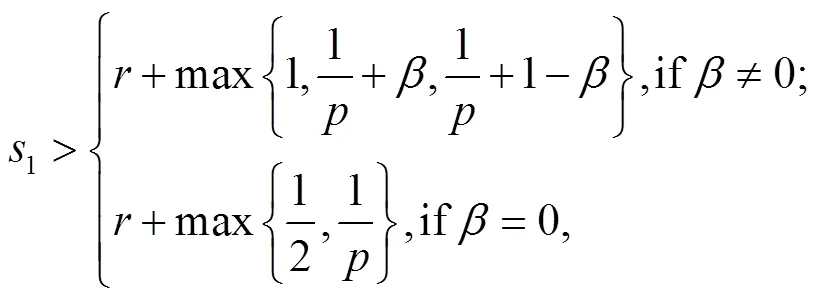
1 准备知识和先验估计

本文先给出索伯列夫空间中的一些不等式，然后再给出一个先验估计．

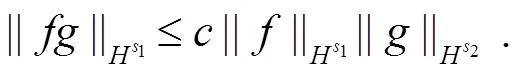
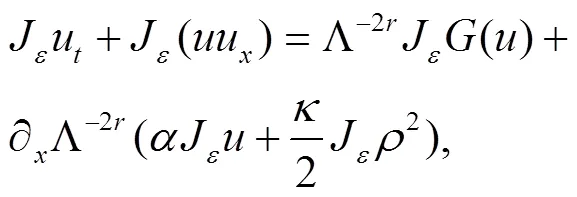
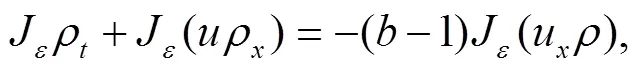
式(5)右边第1个积分可写成如下的形式

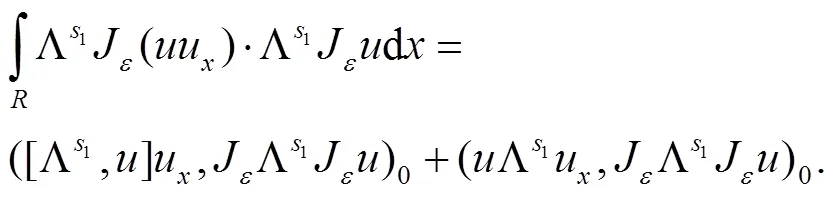
对上式应用柯西不等式和引理1.2(ii)，可得

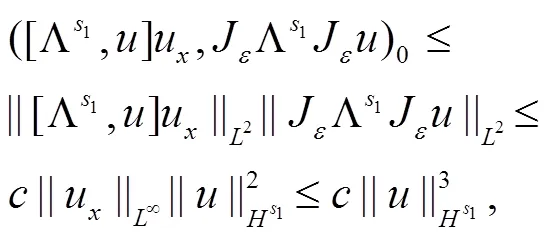
再应用分部积分和引理1.1(i)有

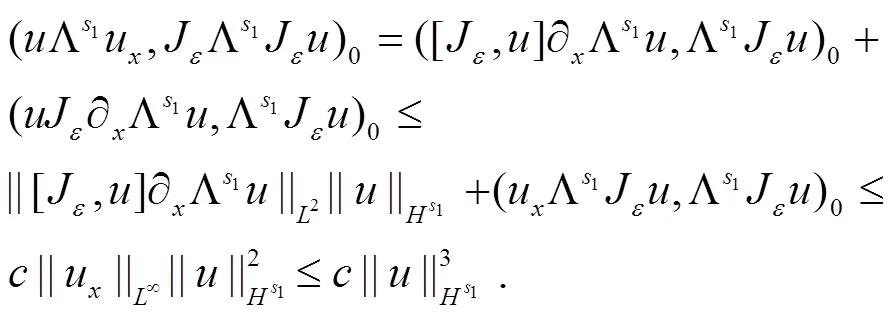
根据式(6)和式(7)则有

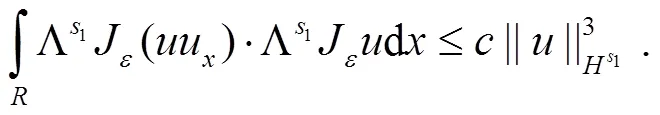
接下来估计式(5)第2个积分，为了简便，本文只估计第一项和最后一项．首先

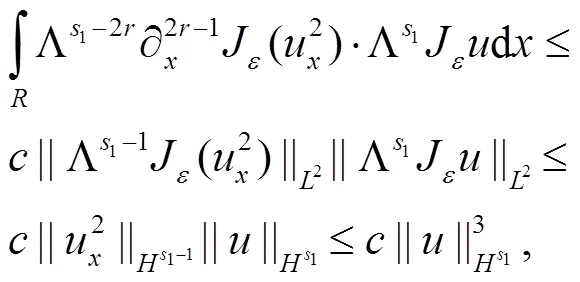
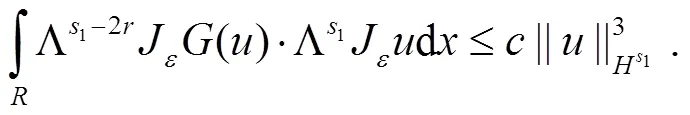
最后估计式(5)右边最后1个积分，即

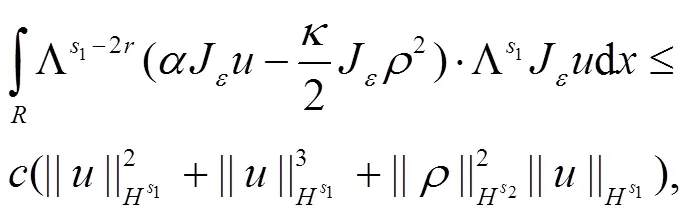
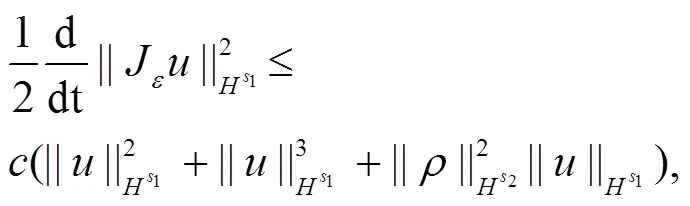
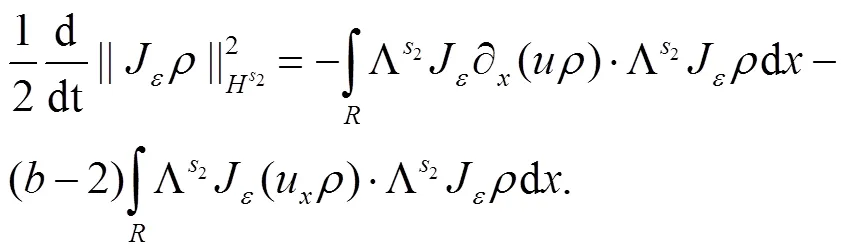
显然，可以把式(14)右边第1个积分写成如下的形式

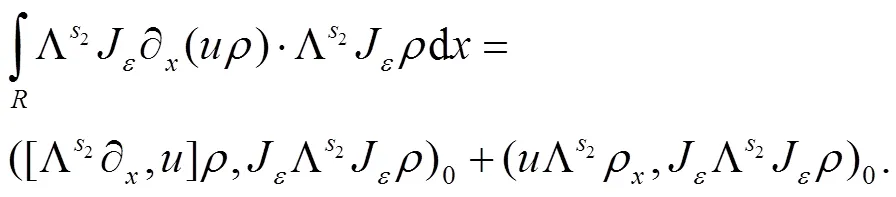
对上式应用柯西不等式和引理1.2(iii)，可得

应用分部积分和柯西不等式有

根据式(15)和式(16)有

可估计式(14)右边的第1个积分，即

根据式(13)和式(19)可得

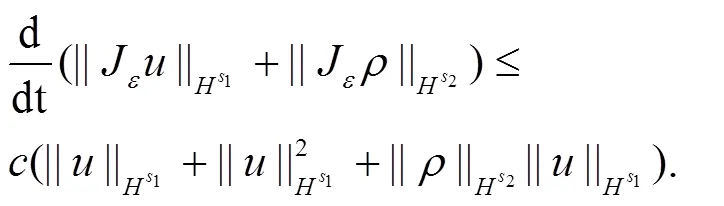
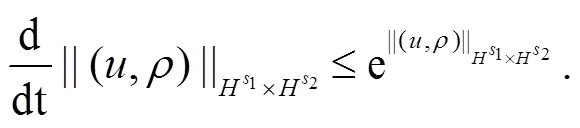
则有

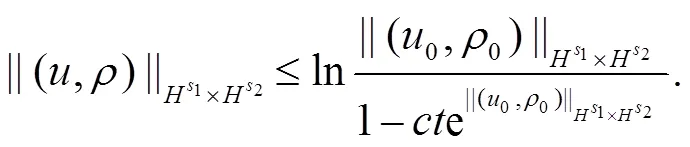
因此，证明了定理1．

2 Hölder连续

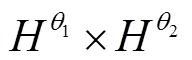
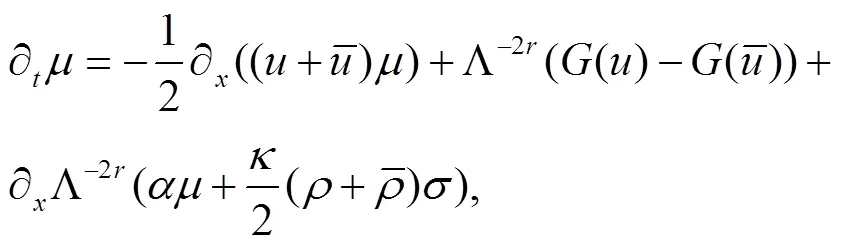
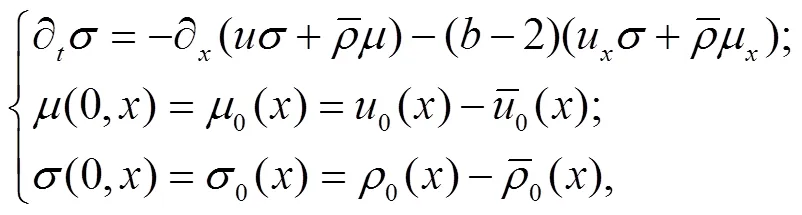
显然，式(25)右边第1个积分可写成如下的形式

应用引理1.2(iii)，估计上式右边第1个积分得

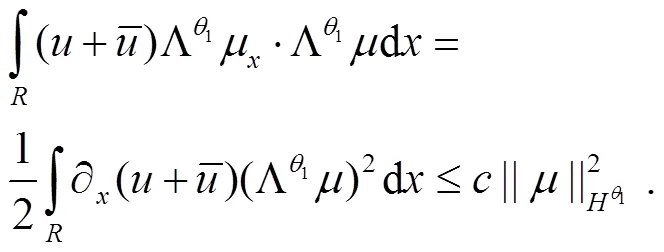
联合式(26)和式(27)可得

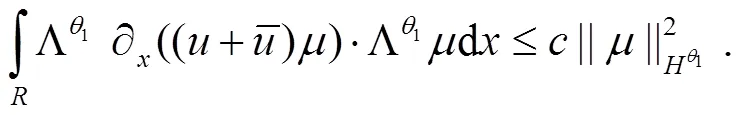
对式(25)右边的第2个积分，本文只估计第一项和最后一项，因此应用引理1.1(ii)可得

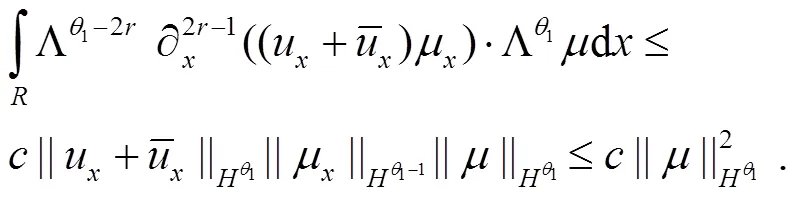
类似的，应用引理1.3可得

联合式(29)和式(30)可得

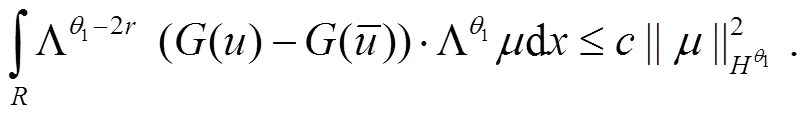
对式(25)右边最后1个积分，有

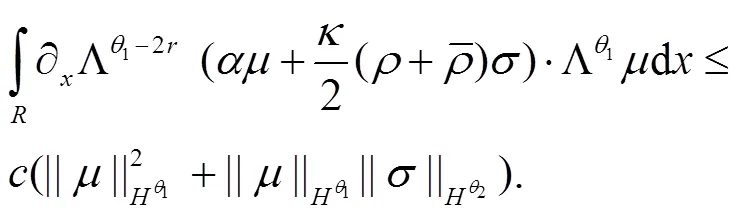
联合式(25)、式(28)、式(31)和式(32)有

对式(24)也可以应用类似的方法得到

因此有

根据定理1有

[1]ESCHER J, LYONS T, Two-component higher order Camassa-Holm systems with fractional inertia operator: A geometric approach [J]. Journal of Geometric Mechanics, 2015, 7(3): 281-293.

[2]HE H J, YIN Z Y. On the Cauchy problem for a generalized two-component shallow water wave system with fractional higher-order inertia operators[J]. Discrete & Continuous Dynamical Systems - Series A (DCDS-A), 2017, 37(3): 1509- 1537.

[3]CHEN R, ZHOU S M. Well-posedness and persistence properties for two-component higher order Camassa–Holm systems with fractional inertia operator[J]. Nonlinear Analysis Real World Applications, 2017, 33: 121-138.

[4]KATO T, PONCE G. Commutator estimates and the Euler and Navier-Stokes equations[J]. Communications on Pure & Applied Mathematics, 1988, 41(7): 891-907.

[5]HIMONAS A A, HOLMES J. Hölder continuity of the solution map for the Novikov equation[J]. Journal of Mathematical Physics, 2013, 54(6): 319-361.

[6]TAYLOR M. Commutator estimates[J]. Proceedings of the American Mathematical Society, 2003, 131(5): 1501-1507.

[7]HIMONAS A A, MANTZAVINOS D. Hölder continuity for the Fokas-Olver-Rosenau-Qiao equation[J]. Journal of Nonlinear Science, 2014, 24(6): 1105-1124.

[8]BAHOURI H, CHEMIN J Y, DANCHIN R. Fourier analysis and nonlinear partial differential equations[M]. Berlin: Springer, 2011.

(责任编校：龚伦峰)

Hölder Continuity for a Two-component High-orderCamassa-Holm System

WANG Bin, ZHOU Shouming*, SONG Xuezhu

(College of Mathematics Science, Chongqing Normal University, Chongqing 401331, China)

From the local well-posedness results of the two-component high-order Camassa-Holm system we know that its solutions depend continuously on their initial data. Based on local well-posedness, we obtain that a priori estimate by Sobolev inequality and energy method. Furthermore, applying interpolation properties of the Sobolev spaces and a priori estimate, we prove that the solution map for the two-component high-order Camassa-Holm system is Hölder continuous.

two-component high-order Camassa-Holm system; Sobolev space; Hölder continuity

TK22

A

10.3969/j.issn.1672-7304.2017.06.0010

1672–7304(2017)06–0046–04

2017-10-27

重庆师范大学科研创新项目(YKC17015)

王彬(1992- )，男，重庆人，硕士研究生，主要从事偏微分方程研究﹒E-mail: wangbin7568@163.com﹒

通讯作者简介：周寿明(1983- )，男，湖北黄冈人，副教授，博士，硕士生导师，主要从事偏微分方程研究﹒E-mail: zhoushouming76@163.com