受损钢框架结构可靠性分析方法研究

胡习兵，江泽普，袁智深，朱 江



受损钢框架结构可靠性分析方法研究

胡习兵1，江泽普1，袁智深1，朱 江2

(1. 中南林业科技大学 土木工程学院，长沙 410018；2. 湖南大象建筑规划设计有限公司，长沙 410004)

通过修正钢结构节点弯矩-转角关系，建立了相应的力学分析模型．利用受损结构的残余变形与承载力之间的关系，构建了受损钢框架结构可靠性分析的目标功能函数；并结合有限步长迭代法和概率网络估计法(PENT法)，提出了受损钢框架结构可靠度计算方法．通过对一榀平面钢框架结构的静力试验研究，获取结构在受损前后的形变参数和极限承载力，采用本文所提出的方法对该结构进行了受损前后的可靠性分析．结果表明：结构体系损伤前后理论承载力与试验承载力吻合良好，提出的受损钢框架结构可靠性分析方法可用于工程实践中损伤钢框架结构的可靠性分析以及极限承载力计算．

钢结构；损伤；可靠度；弯矩-转角关系

随着中国社会的不断发展，钢结构在建筑方面的使用越来越广泛．钢结构在使用过程中难免会受到人为或自然灾害作用而损伤，如：碰撞、过载、火灾、地震、冰灾等都会对钢结构造成一定的损伤[1-3]．这就给人们带来了一个问题——如何判断钢结构在受损之后能否继续投入使用．

国内关于损伤钢结构的安全鉴定与加固仅从节点和构件层面去评定，缺乏损伤钢结构可靠性计算方法，大部分实际检测数据无法引入既有结构安全性评估中．本文根据损伤钢结构形变参数，建立了包含残余转角变形的剩余极限承载力-转角力学模型，进而构建出损伤钢框架结构的功能函数，利用有限步长迭代法[4]和PENT法[5]提出一种计算损伤钢框架结构体系可靠度的方法，为已建损伤钢框架结构的安全性鉴定以及加固提供理论依据．通过对一榀单层单跨损伤钢框架结构进行理论计算与试验对比分析，验证所建立计算方法的有效性和准确性．

1 节点损伤后力学模型

钢结构半刚性节点的弯矩-转角线性模型如图1所示[6]，图中为抗弯刚度，0.1为强化刚度，-0.2为下降段刚度．假设钢结构半刚性节点的弯矩-转角模型为钢结构节点的弯矩-转角一般性模型，损伤截面的弯矩-转角特性可以通过设定抗弯刚度来模拟[7]，则铰接节点的抗弯刚度为=0，刚接节点的抗弯刚度=．

图1 弯矩-转角线性模型

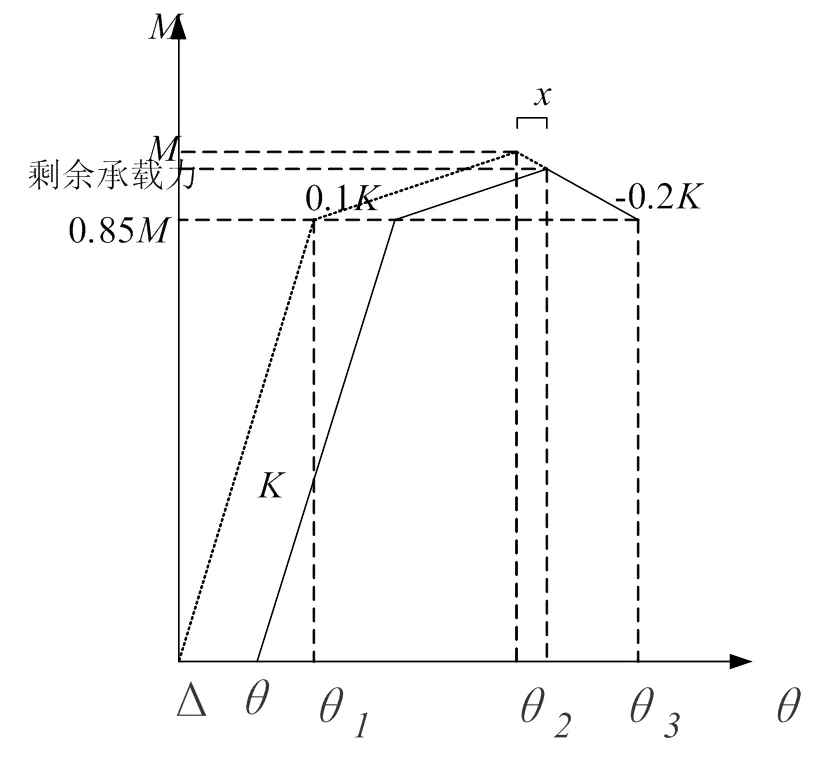
图2 节点损伤后力学模型

根据线性关系有：

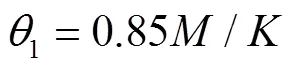
将式(2)、(3)代入式(1)整理得

将式(5)代入式(4)整理得

2 损伤钢框架结构可靠度计算方法

2.1 单一失效模式的可靠性指标计算方法

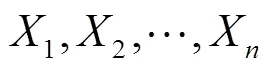
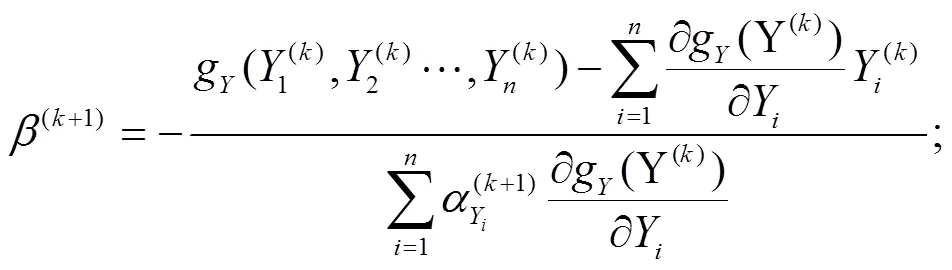
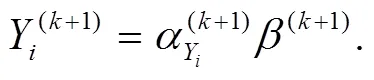
由公式(7)~式(9)构成迭代基本公式，可计算出结构的可靠性指标．

2.2 损伤钢框架结构可靠度计算方法

2.2.1 结构可靠性目标功能函数

2.2.2 单一失效模式可靠性指标

2.2.3 损伤钢框架结构可靠度计算

计算出各失效模式可靠性指标后根据可靠性指标由小到大排序，按顺序计算各失效模式功能函数的相关性系数[9]．由于有限步长迭代法计算可靠性指标时采用了映射变换法，则失效模式间的线性相关系数由下式计算：

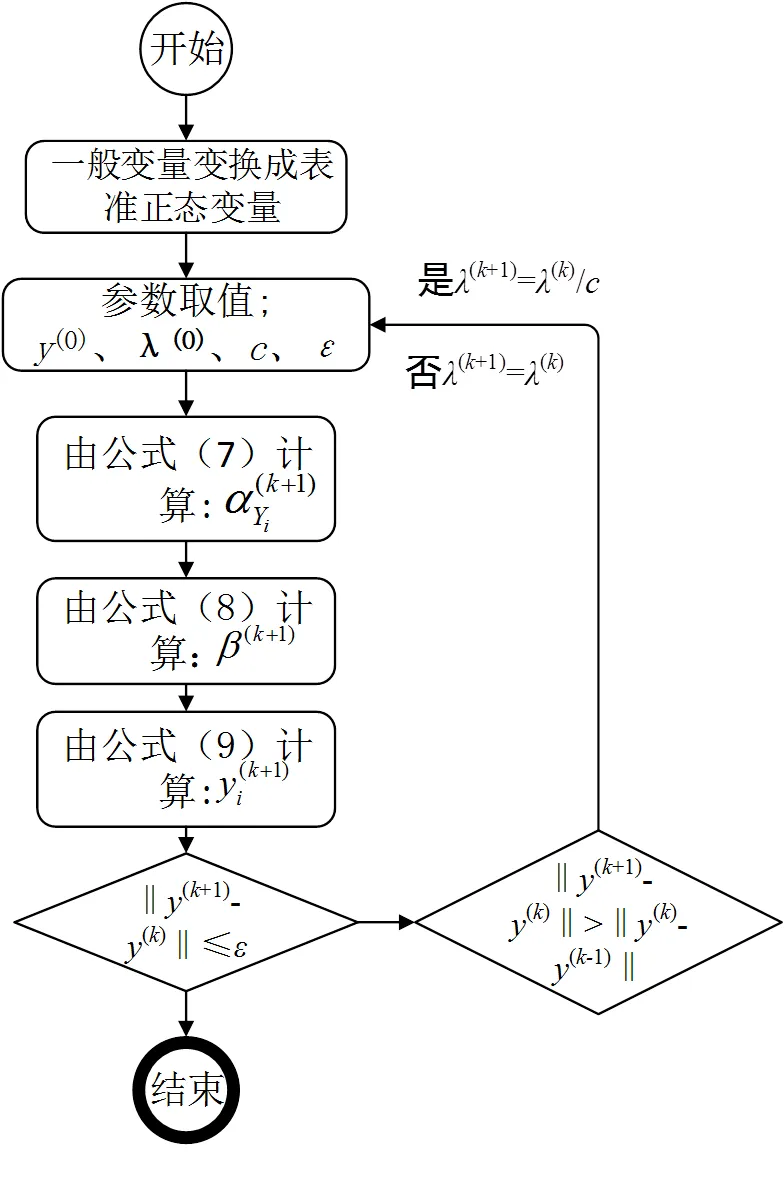
图3 有限步长迭代法流程图

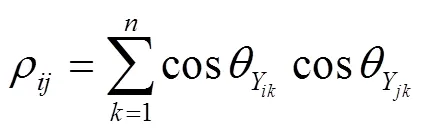
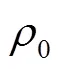
3 试验验证

3.1 试验测试

3.1.1 试验情况

如图4所示单跨单层平面钢框架，梁柱均采用工字型截面杆件，梁柱截面参数如图5所示，柱截面为H125×125×6×8，梁截面为H200×100×6×6，采用Q345B钢材，材料的弹性模量为185 GPa，材料的密度为7.85×103kg/m3，=1.2 m、=1 m；、加载顺序为：先加载竖向荷载=40 kN，保持竖向荷载不变逐渐施加水平荷载到极限荷载．计算在、作用下此框架体系的可靠度．

图4 单层框架结构计算简图

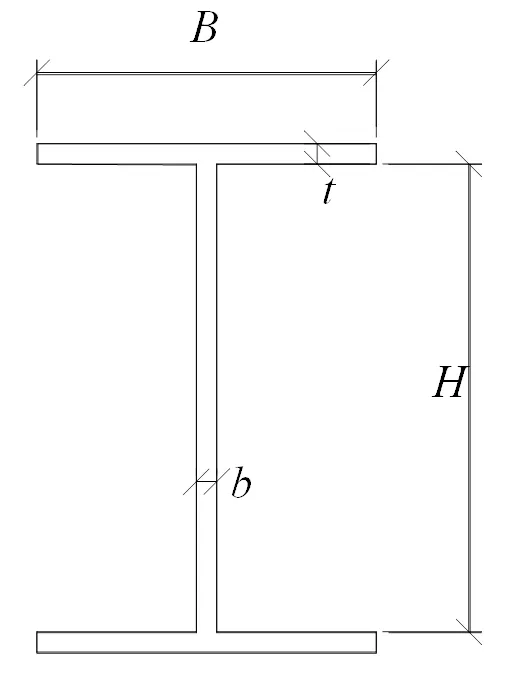
图5 构件截面参数图

影响结构体系可靠性随机变量和设计变量的统计特性见表1和表2．

表1 随机变量统计特性

表2 设计变量初始值 mm

注：设计变量服从正态分布，其变异系数取0.015．

(1)计算变量取值说明．

1)随机变量和设计变量均相互独立．

3.1.2 试验结果

在竖向荷载不变的情况下对如图6所示试验装置进行水平荷载加载，损伤前后水平极限荷载承载力分别为165 kN、148 kN．

图6 试验加载装置图

由试验得到的损伤前后钢柱柱顶位移变化曲线[10]如图7所示．

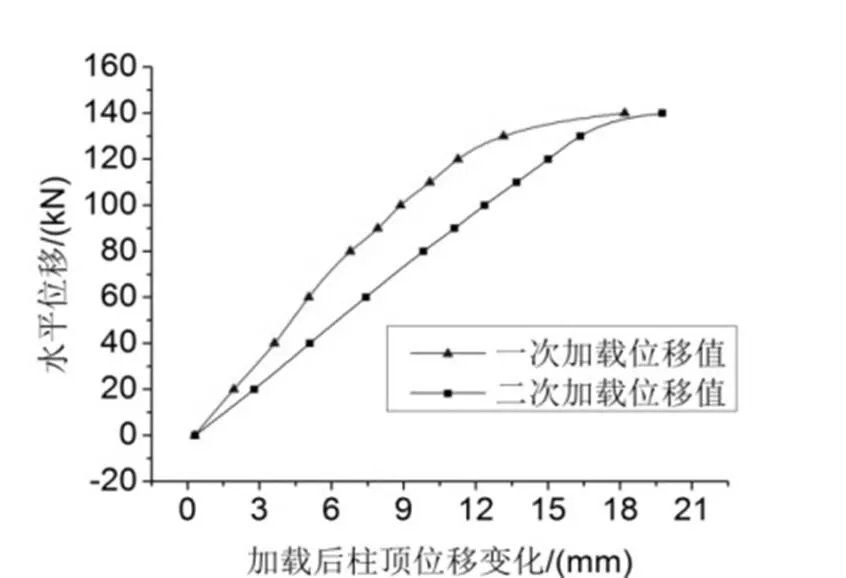
图7 损伤前后钢柱柱顶位移变化

3.2 未损伤钢框架结构可靠度计算

3.2.1 各失效模式的功能函数

平面钢框架可能出现塑性铰的位置有8个，如图8所示，钢框架有3个多余约束，根据分支-约界法[8]可以确定失效模式有6种，利用虚功原理可得各失效模式的功能函数，见表3．

图8 结构可能产生塑性铰位置图

表3 各失效模式的功能函数

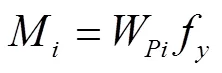
3.2.2 各失效模式的可靠度指标β

对各失效模式按流程图编程计算，最终可靠指标为=(0.016 4，0.363 5，-0.032 4，3.248 4，0.379 5，2.646 3)T．

3.2.3 结构体系可靠度指标β

各失效模式的失效概率如表4所示按从大到小的排列序号：=(3, 1, 2, 5, 6, 4)．计算可得相关系数如表5所示．

代表失效模式为③、⑥，可计算得到单跨单层平面框架结构体系的可靠度及可靠性指标：

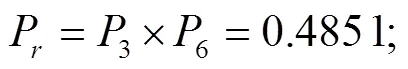
3.3 损伤钢框架结构可靠度计算

3.3.1 损伤后各失效模式功能函数

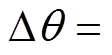
表4 各失效模式的可靠性指标及可靠度

表5 各失效模式间的相关系数

表6 受损后各失效模式的功能函数

3.3.2 受损后各失效模式的可靠度指标β

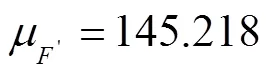
3.3.3 受损后结构体系可靠度指标β

各失效模式的失效概率如表7所示，按从大到小的排列序号为：=(1, 3, 2, 5, 6, 4)．受损后各失效模式功能函数的相关性系数如表8所示．

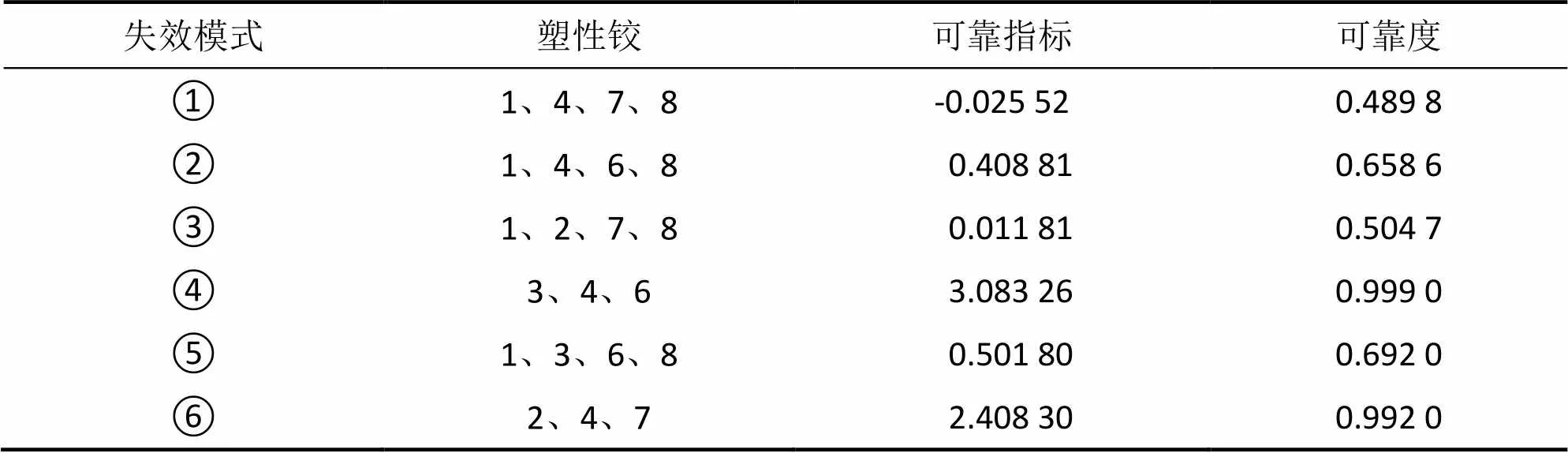
表7 受损后各失效模式的可靠度

表8 受损后各失效模式间的相关系数

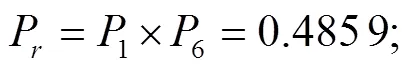
3.4 损伤前后承载力对比分析

(1)钢结构节点损伤后抗弯极限承载力随节点残余转角的增大而减小，损伤后节点抗弯极限承载力最大下降7.91%．

(2)在保证受损前后钢框架结构体系可靠度基本一致以及竖向荷载相同的前提下，受损后结构体系的水平荷载承载力为153 kN，下降了7.27%．

4 结论

(1)用文中所提出的考虑节点残余转角的弯矩-转角模型计算出来的承载力下降幅度与试验数据吻合度较高，能有效地考虑损伤对节点极限承载力的影响．

(2)损伤后实验加载最大水平荷载极限承载力148 kN，与用损伤钢框架结构体系可靠度计算方法计算出来的理论极限承载力吻合良好，能为已建损伤钢框架结构的安全性鉴定提供理论依据．

[1]时虎. 钢结构防火保护研究[D]. 合肥: 中国科学技术大学, 2003.

[2]李国强, 陈素文. 从汶川地震灾害看钢结构在地震区的应用[J]. 建筑钢结构进展, 2008, 10(4):1-7.

[3]侯理哲, 高雅, 刘明旻. 冰雪灾害中的钢结构塔架[J]. 控制工程, 2010(3): 45-47.

[4]贡金鑫. 工程结构可靠度计算方法[M]. 大连: 大连理工出版社, 2003(09): 123-133.

[5]ANG H S, MA H F. On the reliability of structural systems[J]. Proceedings of International Conference on Structure Safety and Reliability.Trondheim, 1981(7): 33.

[6]石文龙. 平端板连接半刚性梁柱组合节点的实验与理论研究[D]. 上海：同济大学, 2006.

[7]胡习兵, 杨雨薇. 受损钢结构力学分析模型研究[J]. 计算力学学报, 2016, 33(1): 128-134.

[8]武清玺. 结构可靠性分析及随机有限元法[M]. 北京: 机械工业出版社, 2005.

[9]赵国藩, 金伟良, 贡金鑫. 结构可靠度理论[M]. 北京: 中国建筑工业出版社, 2000.

[10]陈雅芳. 受损钢框架结构力学性能实验研究[D]. 长沙: 中南林业科技大学, 2017.

(责任编校：陈健琼)

The Analysis for Reliability of Damaged-Steel Frame Structure

HU Xibing1, JIANG Zepu1, YUAN Zhishen1, ZHU Jiang2

(1. College of Civil Engineering, Central South University of Forestry and Technology, Changsha, Hunan 410018, China; 2. Hunan Elephant Architectural Planning & Design Co., Ltd, Changsha, Hunan 410004, China)

A corresponding mechanical analysis model is established by modifying the moment and corner relation of the semi-rigid joint of steel structure. By means of analyzing the relation between the residual de-formation and bearing capacity of the damaged structure, the objective function of the reliability analysis of the damaged steel frame structure was found. Furthermore, combined with the finite step iteration method and the PENT method, the calculation method for damaged steel frame structure reliability was proposed. Finally, through the static test of a plane steel frame structure, the deformation parameters and the ultimate bearing capacity of the structure before and after the damage were obtained, and the reliability analysis was conducted by the method proposed in this paper. The results show that the theoretical bearing capacity of the structural system coincides well with the experimental bearing capacity. The proposed reliability analysis method for the damaged steel frame structure can be applied to the reliability analysis and ultimate bearing capacity calculation of damaged steel frame structures in engineering practice.

steel structure; damaged; reliability; moment-rotation relation

TU323.5

A

10.3969/j.issn.1672-7304.2017.06.0001

1672–7304(2017)06–0001–06

2017-11-04

住房和城乡建设部科技计划项目(2016-K5- 054)；国家自然科学基金项目(51608544)；湖南省教育厅科研项目(14B187)

胡习兵(1973-)，男，湖南桃江人，博士，副教授，主要从事钢结构研究．E-mail: hxb_is_me@126.com