某野战火炮扭杆平衡机纵向布置研究

梁兴旺，李 强，安俊斌，2

(1.中北大学 机电工程学院，山西 太原 030051; 2.中国人民解放军75130部队，广西 贵港 537100)

现代火炮由于多方面原因，在结构布置时起落部分质心不与耳轴中心重合，这样就产生当赋予炮身高射角时费力、而小射角时存在冲击的现象，为了解决这一问题，平衡机就应运而生[1]。根据产生平衡机力的弹性元件不同，平衡机可分为弹簧式、气压式、气液式和扭杆式[2]。

扭杆平衡机具有结构简单、紧凑，质量轻，扭杆不易疲劳损坏，维修简单等优点[3]。扭杆是一个弹性杆件，当其扭转变形时可产生抵抗扭转的力矩。刘威[4]以某重型火箭为原型设计了一种横向布置的扭杆平衡机，其与摇架的连接方式为四连杆机构。刘明勇等[5]设计了一种用于开关舱门的扭杆簧，其一端固定在方舱底壁上，另一端与方舱后门连接；王力生[6]研究了扭杆平衡机在大型车载天线上应用，其扭杆与天线座的连接方式仍为连杆连接。鲜有扭杆式平衡机在野战火炮上进行应用的报道，这是由于扭杆产生的扭矩方向与扭杆轴心在同一直线上，若直接用扭矩平衡重力矩，则必须将扭杆与身管方向垂直布置，即为横向布置，通常扭杆的长度较长，而野战火炮的横向尺寸较小，不足以安装扭杆式平衡机。为解决这一问题，针对野战火炮的特点，并参考德国PzH 2000火炮采用牵引链条连接扭杆平衡机与火炮起落部分[7]，笔者提出了一种扭杆平衡机纵向布置的方案，将扭杆布置在摇架上。

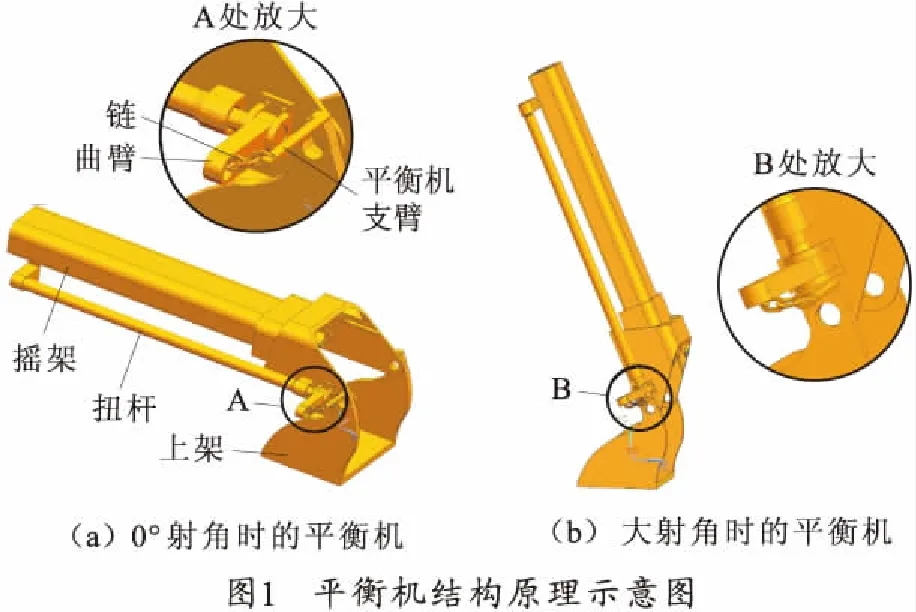
1 扭杆平衡机结构原理

在该方案中，扭杆平衡机前端与摇架固结，后端通过曲臂与上架连接，为协调曲臂与平衡机支臂之间的相对运动，曲臂与上架之间通过起重用链条连接。由于链条只能提供拉力，故本设计采用上拉式平衡机。此时，平衡机后支点在耳轴前方，且链条一端与扭杆曲臂连接，另一端与上架上的平衡机支臂相连接。当火炮处于0°射角时，通过外力使得扭杆产生一个扭转力，此时曲臂通过起重链与平衡机支臂相连接，起重链的拉力为平衡机力。当起落部分俯仰时，扭杆随着起落部分一起转动，由于此时曲臂与平衡机支臂之间的相对位置改变，扭杆曲臂由于扭转力的作用向下转动，直到链限制其转动为止，此时链上的平衡机力改变。其原理示意如图1所示。

2 平衡机的分析与计算

2.1 平衡机的几何分析

因为平衡机的后支点与摇架相连接，故曲臂与链条的连接点相对于耳轴中心做旋转运动。平衡机力Fp由链条提供，而链条只能拉伸不能压缩，故链条与曲臂的连接点的运动轨迹为绕链条上连接点的圆周运动。曲臂与链条的链接点的运动轨迹为绕着扭杆的截面中心旋转的圆周运动。平衡机的3个运动轨迹如图2所示。

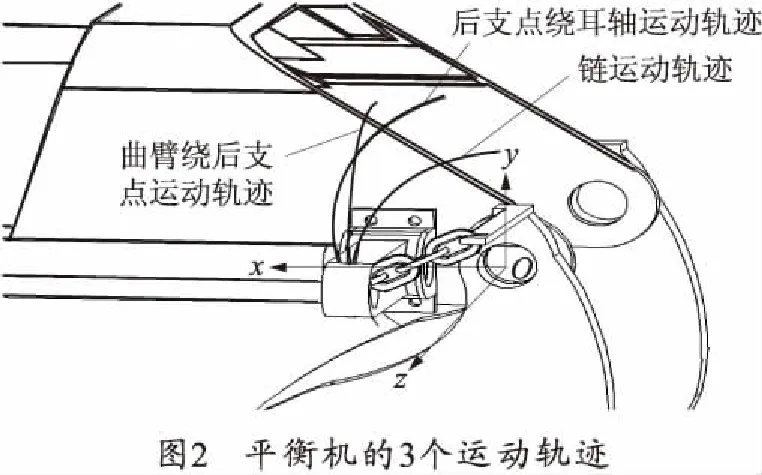
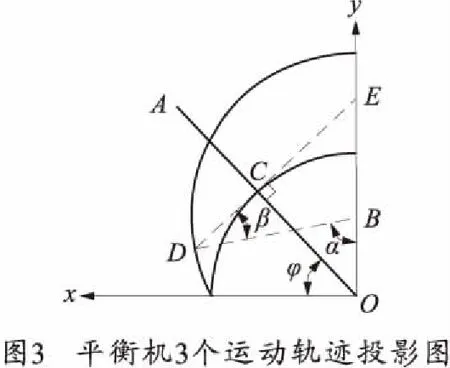
为研究方便，将上述3个运动轨迹投影到Oxy平面上,如图3所示。图中，O为耳轴中心；B为链的上连接点；C为平衡机后支点；D为曲臂与链的连接点；φ为射角；OA为身管轴向；LBD为链在Oxy平面上投影长度；LCD为曲臂与链连接点运动轨迹的投影；以O为圆心的圆弧段为平衡机后支点运动轨迹的投影；以B为圆心的圆弧段为链下连接点的运动轨迹投影。

2.2 平衡机的受力分析

平衡机的平衡力矩为

Mp=ηFpLOBsinα

(1)

式中:Fp为平衡机力，方向为从D到B；η为平衡机的效率，取η=0.96。

在确定了平衡机的结构方案以及尺寸后，可以得到在各个射角下所需要的平衡力矩。

由图3可知，由于

(2)

式中：α=β+φ；Mq为重力矩。

(3)

故此时可得到在各个射角下所需的平衡机力，可以计算出所需要的扭转力

P=Fpcosβ

(4)

本方案采用两点平衡法，故可以得到各个射角下扭杆所能提供的扭转力以及扭转力矩。通过式(4)计算出扭杆所能提供的平衡机力,再由式(1)求出扭杆所能提供的平衡力矩。

不平衡力矩指重力矩与平衡机力矩之差，在本设计中，由于平衡机布置在摇架上，故平衡机会对耳轴中心产生一个重力矩Mphj，在考虑起落部分的不平衡力矩时，必须考虑此力矩。

ΔM=Mq+Mphj-Mp

(5)

2.3 扭杆基本尺寸的设计计算

由以上分析可知，扭杆曲臂的所受到的扭转力已知，因此可以求出扭杆所受到的扭转力矩T。即T=P×R，R为曲臂长度。

为确定曲臂长度R，首先需确定曲臂端点处即曲臂与链的连接点处相对于起始位置位移，即为图3中LCD的长度。

(6)

由此可计算出LCD的最大值，曲臂的长度应大于该长度，考虑到为了使扭杆的扭转角尽量小，并且平衡机的横向尺寸尽可能地小，综合考虑选定曲臂的长度。

在已知LCD与曲臂长度R后，可以求出在各个射角下扭杆的扭转角γ，并可求出在最大最小射角时的扭转角之差Δγ。此时，可以求出扭杆的刚度系数

C=ΔT/Δγ

(7)

式中：ΔT为扭转力矩之差；Δγ为扭转角之差。

则可求得扭杆的最大扭角为

θmax=Tmax/C

(8)

按照以下基本公式可计算出所需要的扭杆直径d和工作长度l，即

(9)

(10)

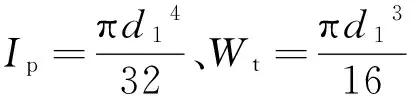
3 某野战火炮的平衡机计算分析

3.1 某野战火炮平衡机受力分析

已知某野战火炮起落部分质量为1 050kg，起落部分质心距离耳轴中心0.761m，该火炮的高低射界为0°～70°。

由已知数据可以计算出该火炮在各个射角下的重力矩Mq=1 050×9.8×0.761×cosφ，如图4所示。

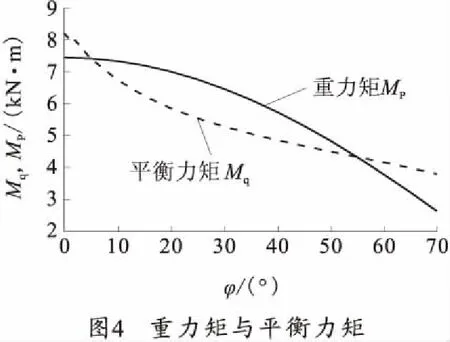
由式(2)可知，为求得所需的平衡机力，需先确定LOBsinα的大小，考虑到耳轴有一定的大小，链条直径不能过大以及其他因素，故LOBsinα不能太小，取LOBsinα最小值为50 mm，并定平衡机后支点距离耳轴100 mm，此时α=30°，可求得链的长度为120 mm。此时可由式(2)求得所需要的平衡机力如图5所示。

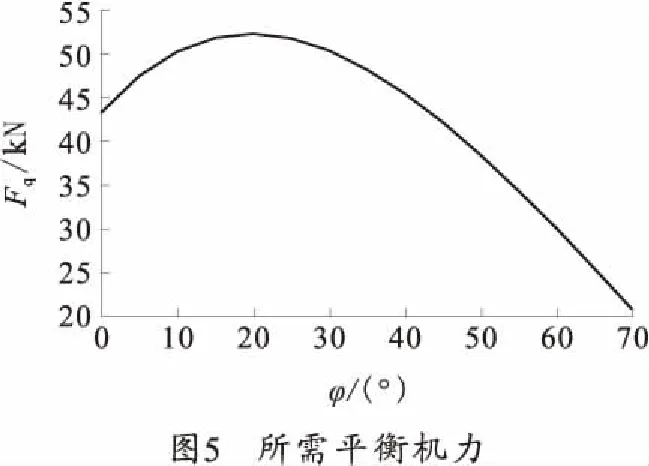
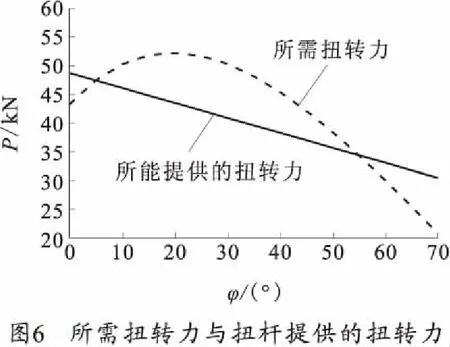
在得知所需要的平衡机力后，依据式(4)可以得到扭杆所需要的扭转力矩。针对某野战火炮采用在5°射角和55°射角处平衡的两点平衡法，可以得到扭杆所能提供的扭转力如图6所示。由式(1)可以得出平衡机所能提供的平衡力矩如图4所示。

3.2 某野战火炮平衡机扭杆基本参数计算

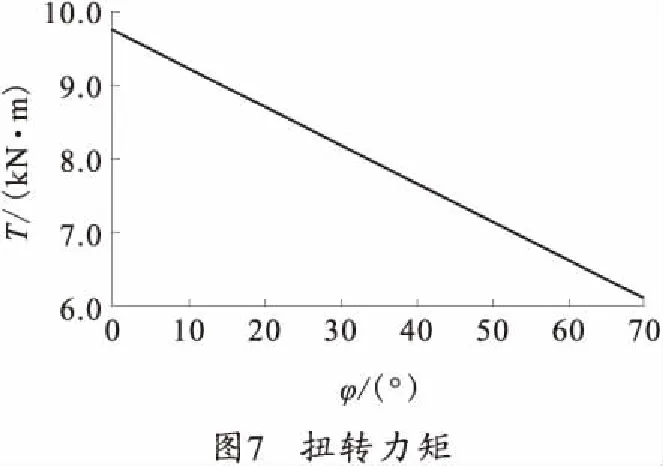
为确定曲臂长度R，需求出各个射角下LCD的长度，在式(6)中，LBD为链的长度，为120 mm，LOC为平衡机后支点与耳轴中心的距离，为100 mm。此时各个射角下LCD的长度可求，求得LCD最大长度为91.27 mm。曲臂长度R应大于这一长度，考虑到应使扭杆扭转角尽可能小，取曲臂长度R=200 mm，故可求得扭杆的扭转力矩T如图7所示，其最大扭转力矩Tmax=9.752 9 kN·m。同时各个射角下扭杆的扭转角可知，γ=arcsin(LCD/R)。此时由式(7)求得扭杆的刚度系数为C=154.8 N·mm·rad-1，再由式(8)可求出扭杆的最大扭角θmax=63°。

在本设计中，采用实心扭杆与空心扭杆串联作为弹性元件,由式(8)、(9)可以求得实心扭杆直径d1=40 mm，空心扭杆内径d2=50 mm，外径D=56 mm。实心扭杆长度为1.5 m，空心扭杆长度为1.4 m。至此，扭杆的基本尺寸计算完毕。

设计完成的扭杆式平衡机质量为30 kg，其质心距离耳轴中心为0.626 m。此时可由式(5)求出不平衡力矩如图8所示。

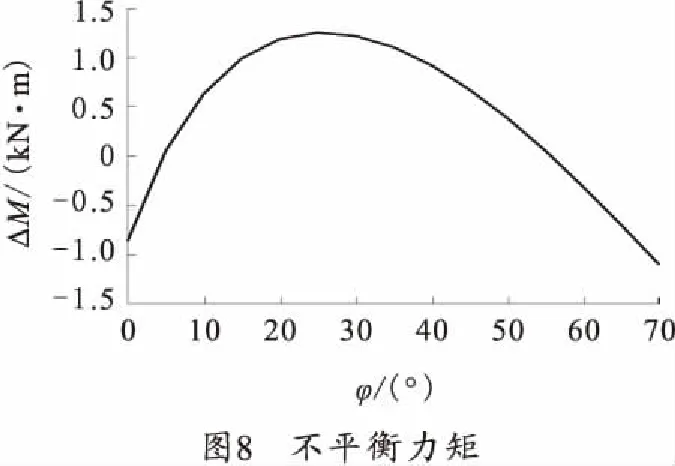
由图8可以看到，不平衡力矩最大值发生在射角为20°到30°之间，最大不平衡力矩小于1.5

kN·m。

3.3 关重件强度分析

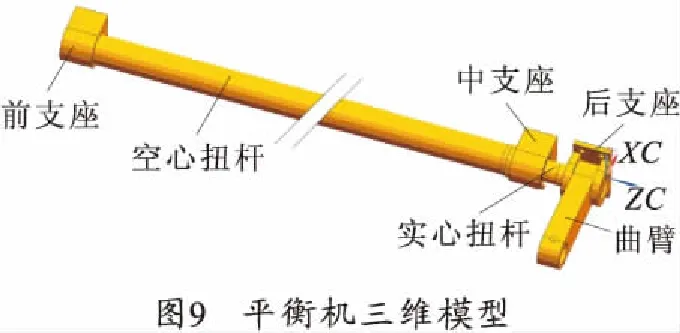
在确定了实心扭杆和空心扭杆的基本尺寸后，对实心扭杆及空心扭杆的具体结构进行设计，并且对平衡机的其余零部件进行相应的设计，并利用UG对结构进行三维建模，模型如图9所示。

3.3.1 模型的边界条件及载荷

通过对平衡机进行有限元仿真分析，可以得知平衡机的受力状态。笔者利用ABAQUS有限元分析软件对平衡机进行仿真分析。

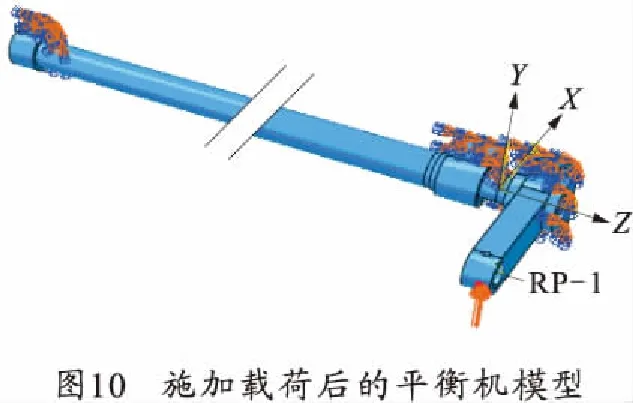
将UG中的三维模型导入ABAQUS中，并对各部件施加约束以及边界条件。对平衡机前支座，后支座以及曲臂支座施加固定约束，限制其6个方向的自由度；对实心扭杆端头与空心扭杆端头、实心扭杆端头与曲臂之间以及空心扭杆端头与平衡机后支座之间进行绑定约束，用来模拟其花键细齿连接；其余部分均采用通用接触设置，设置摩擦系数为0.05。按照平衡机的受力情况，对平衡机的销施加载荷，由于平衡机力可分解为扭转力以及与之垂直的力，故将平衡机力分解为两个方向上的分力。施加载荷后的平衡机模型如图10所示。

3.3.2 仿真结果分析

由于本计算模型涉及实心扭杆空心扭杆的大变形问题，故在ABAQUS中设置求解模式为几何非线性，并采用动力显式(Dynamic，Explicit)求解。

在扭杆设计当中，值得关心的是扭杆所受到的切应力，为求得扭杆的切应力，将求解完的模型转换为圆柱坐标系，扭杆所受到的切应力云图如图11所示。实心扭杆与空心扭杆表面的切应力随扭角的变化曲线如图12所示。

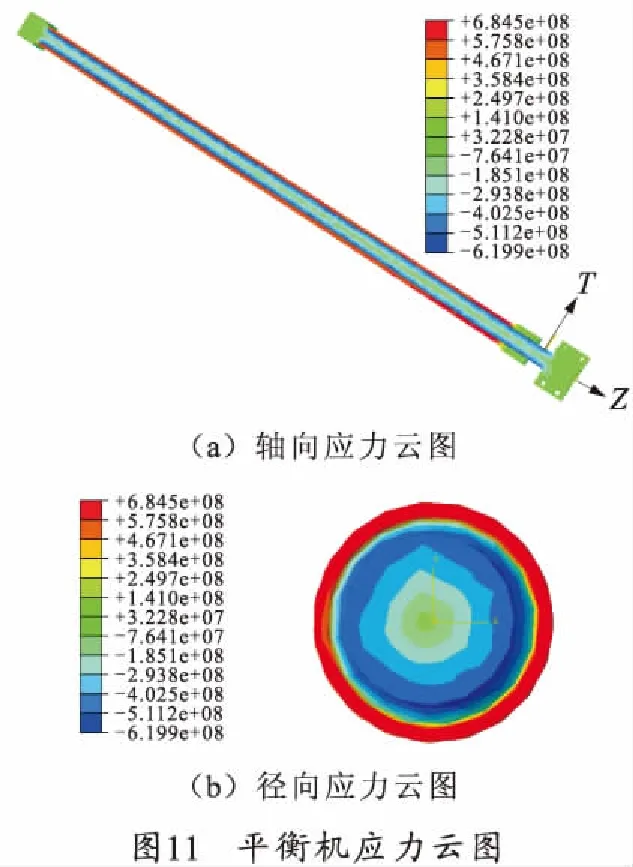
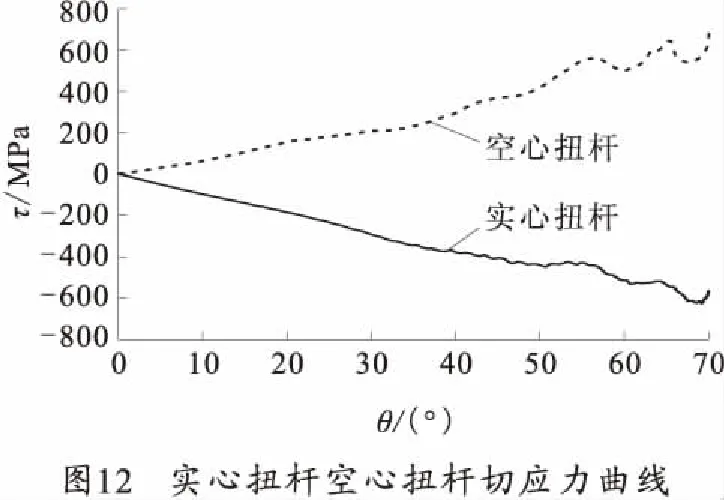
由切应力云图可以看出，实心扭杆与空心扭杆的切向应力随着半径均匀变化，符合实际情况。实心扭杆的最大切应力为-619.9 MPa，空心扭杆的最大切应力为684.5 MPa，均小于材料的许用切应力[τ]=900 MPa[9]。其Mise主应力最大值为1 183 MPa，小于其屈服应力[σs]=1 325 MPa[10]，故实心扭杆空心扭杆的强度符合要求。

4 结束语

该方案以某型榴弹炮为原型，通过分析其空间受力情况，分析了扭杆式平衡机纵向布置在该类野战火炮上应用的可能性，针对野战火炮横向尺寸小、不便布置扭杆式平衡机的问题，提出了将扭杆式平衡机纵向布置的的结构方案，并给出了相应的设计方法。在设计完成后通过有限元分析软件ABAQUS对平衡机进行强度分析，仿真结果显示，该设计的扭杆强度满足要求。基于同样的原理，本文中的设计方法对扭杆式平衡机纵向布置在同类型野战火炮上的应用提供了一种参考。

References)

[1]孙远孝，潘学文. 炮架及总体设计[M]. 北京：兵器工业出版，1995: 100-101. SUN Yuanxiao, PAN Xuewen. Carriage and collectivity design[M]. Beijing: The Publishing House of Ordnance Industry,1995: 100-101.(in Chinese)

[2]张相炎，郑建国，袁人枢.火炮设计理论[M].北京：北京理工大学出版社，2014:276-284. ZHANG Xiangyan, ZHENG Jianguo, YUAN Renshu. Theory of artillery gun design[M]. Beijing: Beijing Institute of Technology Press,2014:276-284. (in Chinese)

[3]谈乐斌.火炮概论[M].北京：北京理工大学出版社，2014:198-203. TAN Lebin. Introduction to artillery[M]. Beijing: Beijing Institute of Technology Press,2014:198-203.(in Chinese)

[4]刘威.某扭杆式平衡机设计和疲劳仿真[J].机电工程技术，2015，44(4)：47-51. LIU Wei. Design and fatigue simulation of the torsion bar balancer[J]. Mechanical & Electrical Engineering Technology，2015，44(4)：47-51.(in Chinese)

[5]刘明勇，高尚雪，刘勇，等.扭杆弹簧的设计及应用[J]. 机械设计，2011,28(12):93-96. LIU Mingyong, GAO Shangxue，LIU Yong，et al. Design and application of torsion bar spring[J].Journal of Mechine Design, 2011, 28(12):93-96. (in Chinese)

[6]王力生.扭杆平衡机构在大型车载天线中的应用及优化[J].现代电子技术，2005,28(7):111-113. WANG Lisheng. Application and optimization of torsion bar blance mechanism in large vehicle carried antenna[J]. Modern Electronics Technique,2005,28(7):111-113. (in Chinese)

[7]卫锦萍. 德国PzH 2000式155 mm自行榴弹炮[J]. 现代兵器, 1992(8):21-23. WEI Jinping. The German PzH 2000 155 mm self-propelled howitzer[J].Modern Weapons, 1992(8):21-23. (in Chinese)

[8]刘鸿文.材料力学[M].北京：高等教育出版社，2011:78-87. LIU Hongwen. Mechanics of materials[M]. Beijing: Higher Education Press,2011:78-87. (in Chinese)

[9]秦大同，谢里阳.现代机械设计手册[M].北京：化学工业出版社，2011,10:122-123. QIN Datong,XIE Liyang. Modern handbook of mechanical design[M].Beijing:Chemical Industry Press,2011,10:122-123. (in Chinese)

[10]孙玉福.实用工程材料手册[M].北京：机械工业出版社，2014:104-106. SUN Yufu. Manual of practicl engineering material[M].Beijing:China Machine Press，2014:104-106. (in Chinese)