可视化技术在公安数学教学中的应用
2017-01-20张东
张东
摘 要: 可视化教学技术已经普及,但针对公安院校数学教学环境及教学目的的特殊性,如何在公安院校数学教学过程中更有效地运用可视化教学技术仍需探讨。本文在对国内公安院校数学教学实际状况进行调研分析后,提出在公安院校数学教学中运用可视化技术的思路,并辅以实例。
关键词: 可视化技术 公安院校 数学教学
当今社会,数学与社会的关系发生根本性变化,数学已经深入从自然科学到社会科学的各个领域。由于最近20年的进步,社会科学许多领域已经发展到不懂数学的人望尘莫及的阶段。现在数学读写能力,也就是量的读写能力正摆在我们的眼前。现代社会许多信息是用量的方式提供的,因而作为一个现代人,用量的方式思维、推理和判断已成为一种基本能力[1]。
作为承担着维护社会稳定职责的人民警察,应当具有比一般民众更强的社会适应能力。因此在培养警务人员的各公安院校中,理当大力发展数学教育,以便为国内警务系统输送更优秀、适应力更强的人才。但不幸的是,国内公安院校没有注意到数学的重要性,数学教育开展受到诸多制约。在这样大环境下,如何尽快提升公安高校的数学教学效率,已是一个亟待解决的课题。对此,我的想法是将普通高校中已经发展得比较成熟的可视化教学技术,经过调整后,引入公安院校数学教学中,以缓解目前公安院校数学教学压力,提升数学教学效率,提高人才培养质量。
一、国内公安院校数学教学环境现状及可视化教学技术发展情况
通过对国内四所省属以上公安院校的调研结果显示,数学教学在公安院校中的开展情况不容乐观。普遍性问题主要集中在以下两个方面:
1.课时不足。各专业制订培养方案或教学计划,往往由于需要开设的课程太多,课时不够分配而将数学类课程课时压缩或干脆不开。部分院校出现了刑事侦查技术、经济侦查等技术类专业不开设高等数学课程的情况。即使是那些开设了数学课程的专业(多为信息安全、网络安全等计算机专业),数学类课程课时往往只能达到普通地方院校同类课程课时的二分之一至三分之二,课时严重不足。
2.数学课堂教学以系统数学知识讲授为主,缺乏对学生数学能力的开发和培养[2]。致使学生学习数学的主动性降低,不能体会数学实际价值,更不会主动用数学语言描述问题。
要解决这些客观存在的问题,我们必须抓住公安数学教学注重实用、实战的特点,借助可视化辅助教学方法解决。
进入二十一世纪以来,随着计算机技术的迅速发展,一些数学软件出现以其强大的数值计算、符号运算和生动的图像处理等功能替代传统数学方式下用纸和笔进行的操作,数学可视化教学技术逐渐完善。数学教育中使用计算机可视化辅助教学的目的在于“通过提出问题,利用可视化技术创设直观情境,沟通新旧知识间的内在联系,以可视引导思维,启迪学习者认识数学对象的本质特征”[3]。
二、在公安院校应用可视化教学的特殊性及指导思想
虽然可视化教学技术已经比较成熟,但由于目前国内公安院校数学教学环境的现状及教学目标的特殊性,当我们将可视化教学技术应用到公安数学过程中时,必须对它进行调整,让它在这种特殊环境下发挥作用,帮助我们更好地完成数学教学工作,培养优秀的公安人才。这种调整的指导思想是:弱化理论,强化应用。所谓“弱化理论”,指的是对于大部分公式、定理,只需要让学生大概了解这些公式都是从哪里来的,它们说明了一个什么问题就可以。而没有必要让学生做到“可以推导出公式,可以快速计算”。“强化应用”其实是要求学生掌握每一个定理或公式可以解决什么问题,在怎样的情况下可以(如何)使用。
为什么要“弱化理论”,有两个原因:第一,这是在公安院校数学教学课时和资源均不足的情况下做出的选择,目的是节省出更多时间“强化应用”。第二,公安院校学生走上工作岗位后,绝大部分人都会走向公安一线,没有多少机会从事理论研究工作,但对所学内容的实用性却有着很高的要求,因此数学对他们而言应该是工具。第三,在计算机科学和互联网技术如此发达的现在,越来越多的工作可以由计算机完成,而人的主要任务则是做“决策”。比方说学生只需要知道可以使用某公式分析当前问题,就可以快速从计算软件中调出该公式,余下的工作都可以交给计算机。
在这种指导思想下,可视化教学任务将从“帮助学生更快、更好、更系统地理解概念、原理”变成“以可视化的内容,取代部分公式化的推导,以便学生更快地了解讲授的内容(同时影响更深刻)”。这实际上对授课教师的课堂设计提出更高的要求。
三、应用实例
高等数学中一元函数连续与可导的相互关系是一个重难点,公式化的证明总是让学生晕头转向。如果借助函数图像说明,借助图像的直观性将会达到出乎意料的良好效果。
对于不连续函数而言,其图像不是一条可以一笔画出的连续曲线,会出现断开的情况。如分段函数f(x)=x+3(x<0)x+2(x≥0),其函数图像在x=0处断开了(如图一),所以函数在该点是不连续的。
连续函数的图像是一条无间断的连续曲线,但不一定是光滑的,期间可能出现折角等不存在切线的点。如绝对值函数f(x)=|x|,其函数图像在x=0处没有断开,但不光滑,因此在该点处是连续但不可导(如图二)。
图二
可导函数在x点处的函数图像是连续且光滑的,存在不垂直于x轴的切线,如函数f(x)=x的图像(如图三)。
对比三个函数图像在x=0处的状态,学生很直观地了解“不连续”,“连续但不可导”及“可导”这三种状态,同时也可以理解“一元函数可导一定连续,连续不一定可导”的关系。这种观察的方式比单纯利用公式推理更直接有效、便于理解。
另外,借助图像帮助理解概念的过程中,要让学生参与进来,学会使用常用数学软件制图。如以上三幅图都可以让学生在课堂上借助Matlab绘制,指令很简单:
绘制函数f(x)+|x|图像“ezplot(′abs(x)′,[-3,3,0,6])”;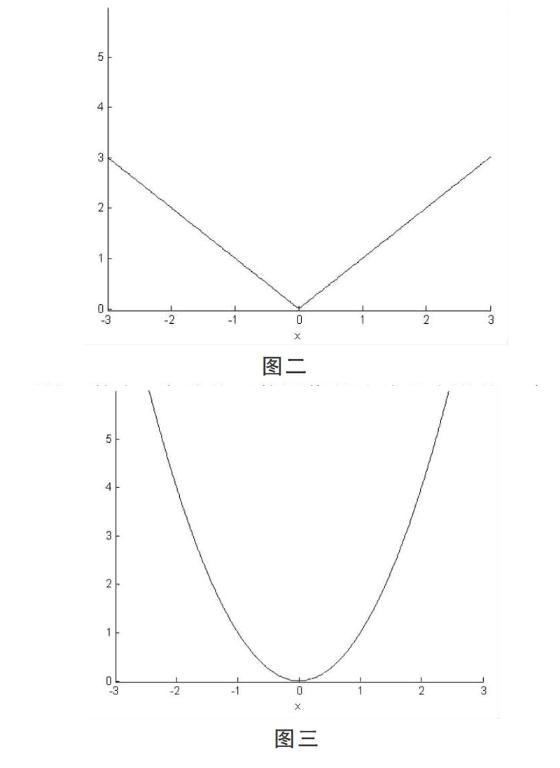
f(x)=x的函数图像“ezplot(′x.^2′,[-3,3,0,6])”;
分段函数在Matlab中要麻烦一点,关键是凸显出它的间断点,因此可以分为两个函数来做,指令为:
hold on
axis([-3,3,0,6]);
x=-3:0;y=x+3;
plot(x,y)
x=0:3;y=x+2;
plot(x,y)
这些简单指令只需要几分钟即可让学生掌握,让学生在学习使用数学软件的过程中掌握必要的数学知识,提高学习兴趣,培养学生的数学应用能力[4]。
参考文献:
[1]美国国家研究委员会.人人关心数学教育的未来.世界图书出版公司,1993.
[2]王秀良.从水池注水问题谈起——兼论公安院校的数学建模教育.中国人民公安大学学报(自然科学版),2010.1.
[3]王丹华,杨海文,刘诗焕.基于几何画板的数学可视化教学探讨.井冈山大学学报(自然科学版),2011.7.
[4]宿维军.基于Maple系统的交巡警务服务平台的设置与调度实验.自动化与仪器仪表,2012.3.
项目基金:湖北警官学院院级教改项目(JYKT2014012)。
