多视角宽思维妙解函数零点问题

江苏省连云港市锦屏高级中学 (222021)

车树勤

多视角宽思维妙解函数零点问题

江苏省连云港市锦屏高级中学 (222021)

车树勤

函数的零点充分体现了函数与方程的联系，蕴含了丰富的数形结合思想.诸如方程根的问题、存在性问题以及交点问题等都可以转化为零点问题来讨论，因而函数的零点成了近年来高考新的热点而备受青睐.下面以一道苏锡常镇的高三调研试题为例来剖析函数的零点问题的解题方法.

一、考题回放

调研试题若函数f(x)=ax-x2(a>1)有三个不同的零点，则实数a的取值范围是________.

思维阶段求一个函数的零点个数，通常是转化为我们熟悉的两个函数看其图像的交点个数，就是零点的个数.而本题的两个函数是y=ax,y=x2，要使两个函数图像有三个交点则要使这两个图像在(0,+∞)有两个交点.指数函数和二次函数的图像都是曲线，该如何让其有两个交点是解决问题的关键.

点评：本解是结合函数图像，根据两个函数图像要有三个交点，明显在第二象限有一个交点，在第一象限要有两个交点.根据相切的时候有公共切线，切线斜率相等，以及该切点满足两个函数关系式列方程，求出相切时候a的值得到其取值范围.

点评：本解法是先取对数后得到方程xlna=2lnx，要使其有两个解，可看作两个函数的图像有两个不同的交点，临界状态是一次函数与对数式函数相切的时候有一个交点，当直线的斜率变小时，两函数图像有两个不同的交点，从而得到a的取值范围.

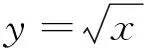
点评：本解法主要是利用互为反函数的函数图像关于y=x对称，所以两个函数图像原来有几个交点，其反函数的图像交点个数不变.方程ax=x2中的x在指数位置，由反函数转化为对数来求.要求方程有两根，在函数图像先减后增的情况下，只要函数的极小值小于零即可.

本题从多个视角对函数零点问题进行了研究.思维1直接从两个函数图像有一个交点时进行探究；思维2先对方程取对数转化为两个函数再进行探究；思维3是把思维2中的方程再变形为一个关于x的函数与一个常数函数进行探究；思维4是利用反函数来看其交点个数.问题的关键在于转化，把未知转化为已知，希望通过此题的解答能在解题时打开思路，多角度进行思考，能起到事半功倍的效果.

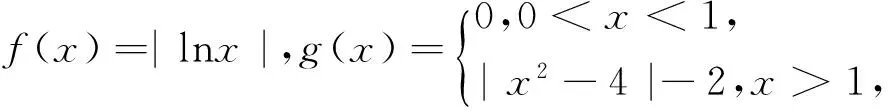
分析：分两种情况去掉绝对值，再把f(x),g(x)的解析式代入方程，画图像看其交点个数.

解：(法一)由题意得：求函数y=f(x)与y=1-g(x)交点个数以及函数y=f(x)与y=-1-g(x)交点个数之和，因为y=1-g(x)=

(法二)f(x)+g(x)=

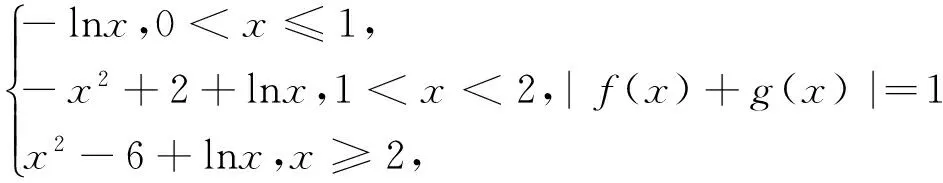
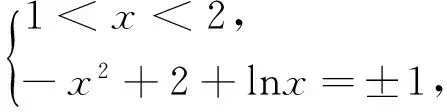
图1

(3)考察

分析：利用函数是减函数，根据对数函数的图像和性质判断出a的大致范围，再根据f(x)为减函数，得到不等式组，利用函数的图像，方程的解的个数，推出a的范围.

解：y=loga(x+1)+1在[0,+∞)递减，则0

二、如何把握函数零点的教与学

从以上近两年的高考函数的零点出现的题型总结分析，我认为在函数的零点教学中应当让学生理解函数的零点的概念及定理，以及能掌握函数的零点题型的解题思路及常见方法.

1.函数的零点的存在性定理

如果函数y=f(x)在区间[a,b]上的图像是连续不断的一条曲线，并且有f(a)f(b)<0，则函数y=f(x)在区间(a,b)内有零点，即存在c∈(a,b)，使得f(c)=0，这个c也就是方程f(x)=0的根.零点存在性定理是函数在某区间上存在零点的充分不必要条件，此定理的逆命题不成立.

2.掌握函数的零点题型的解题思路及常见方法

从以上近两年高考函数的零点题型的分析可以看出，高考对函数的零点问题主要考查以下三个层面：一是利用函数的零点的概念及定理求函数零点的个数及零点所在的范围，这是基础；二是给予一些函数零点的条件，确定其中未知的参数，这是基础内容的提高；三是将函数的零点问题同其他知识结合在一起出综合试题.不论高考如何命题，只要在函数的零点问题的教学中夯实基础，立足课本，掌握函数的零点题型的解题思路及常见方法，注意函数的零点问题与函数、方程、图像等其他知识的交叉融合，就能更好地培养学生综合分析问题的能力及逻辑思维能力.