一道解析几何题的变式拓展
2017-01-20浙江省金华市第六中学321000
浙江省金华市第六中学 (321000)
虞 懿
浙江省丽水中学 (323000)
曹 斌
一道解析几何题的变式拓展
浙江省金华市第六中学 (321000)
虞 懿
浙江省丽水中学 (323000)
曹 斌
每年高考都会留下一份十分宝贵的资源——数学高考试卷,其中许多试题内涵丰富、立意新颖、视角独特,彰显着数学永恒的魅力,也为我们的学习和探究提供了广阔的平台.2013年高考江西理科第20题就是难得的优质高考试题,文[1]对此题进行了探究和拓广,本文在此基础上进行变式拓展,得到了几个好的结果,与诸位分享.

图1
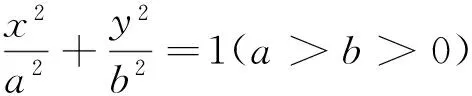
一道好的试题往往是命题者研究成果的结晶,在一个背景下,交换部分条件和结论,或给出某个问题一般结论的特例,便生成出一道新题,又能挑战你的思维.笔者结合对相关题目的研究,又做了如下探究:
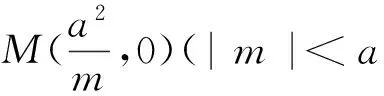
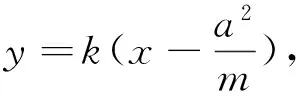
2ma4k2x+a6k2-a2b2m2=0.其中
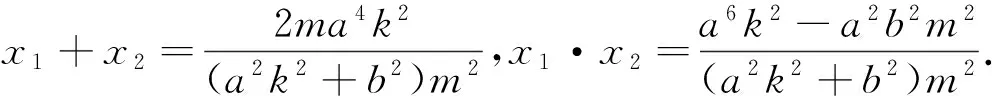
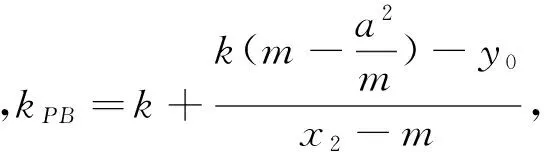
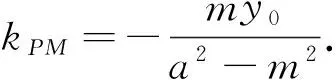
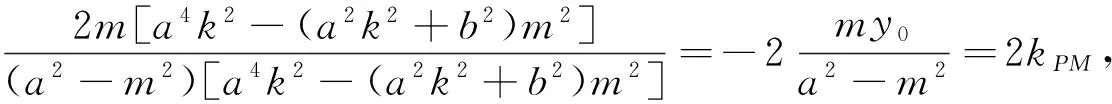
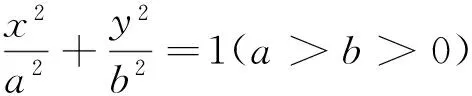
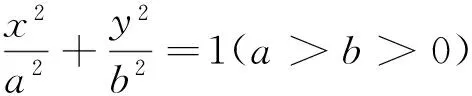
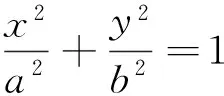
其中Δ=4m2a4k4-4(a2k2+b2)(a2m2k2-a2b2)=4a2b2(a2k2+b2-k2m2)>0.



=2k+[k(x0-m)-y0]
=2k+[k(x0-m)-y0]·
由PA、PM、PB的斜率成等差数列,则
2k+[k(x0-m)-y0]·
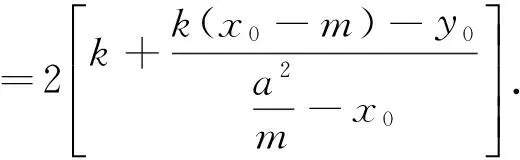
若k(x0-m)-y0≠0,有
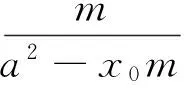
=m(a2k2+b2-m2k2).
而a2k2+b2-m2k2=k2(a2-m2)+b2>0,所以x0=m,即点P在直线x=m上.
综上,点P必在直线AB或直线x=m上.
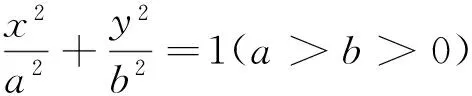
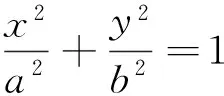

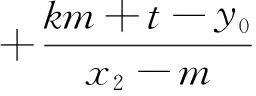
由于直线AB不过点P,则有km+t-y0≠0,
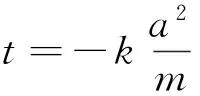
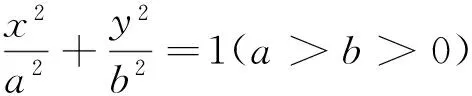
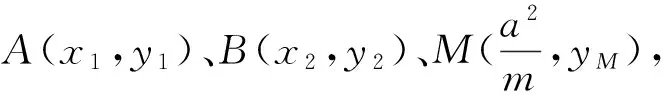
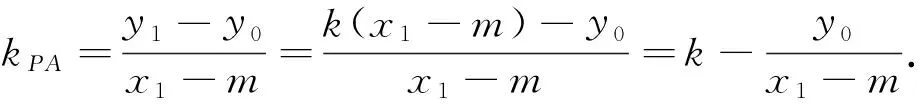


由于直线PA、PM、PB的斜率成等差数列,且
y0≠0,则
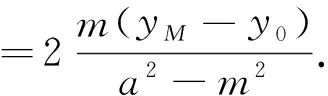
满足直线AB的方程y=k(x-m),从而A﹑B、M三点共线.
上述结论对双曲线、抛物线是否成立呢?留给有兴趣的读者去探究.
[1]张国良.圆锥曲线的一个完美性质—一道2013年江西高考试题的推广[J].中学数学,2014(6).
