特殊相似椭圆的一组性质
2017-01-20北京市陈经纶中学100020
北京市陈经纶中学 (100020)
张留杰
特殊相似椭圆的一组性质
北京市陈经纶中学 (100020)
张留杰
根据相似形的定义,我们不难定义相似椭圆:
如果两个椭圆的长轴和短轴对应成比例,则称它们是相似椭圆.
显然对于中心在原点的两个相似椭圆,其方程可以设为C1:αx2+βy2=1(α>0,β>0且α≠β)和C2:αx2+βy2=λ2,它们的相似比为λ(λ>0且λ≠1).
首先,类比同心圆的性质,给出相似椭圆的一条重要性质定理:
定理相似椭圆C1:αx2+βy2=1(α>0,β>0且α≠β)和C2:αx2+βy2=λ2(λ>1),如图1,过C2上一点P作C1的两条切线PA、PB,交椭圆C2于A、B两点,切点分别为M、N.则M、N分别为PA、PB中点,且OP平分切点弦MN.
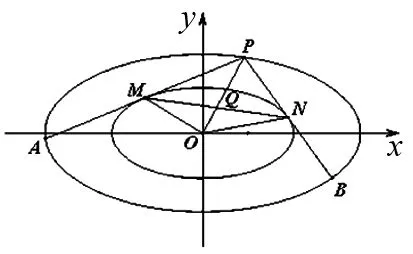
图1
证明:设P(x0,y0),M(x1,y1),N(x2,y2),所以C1的切线PM:αx1x+βy1y=1,PN:αx2x+βy2y=1,将点P(x0,y0)的坐标代入,得αx1x0+βy1y0=1和αx2x0+βy2y0=1,所以切点弦MN所在直线方程为αx0x+βy0y=1.

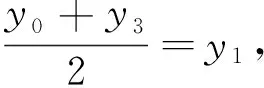
下面探究两对相似比为特殊值的相似椭圆的性质.
命题1相似椭圆C1:αx2+βy2=1(α>0,β>0且α≠β)和C2:αx2+βy2=2,过C2上一点P作C1的两条切线(切线与坐标轴不平行),交椭圆C2分别为A、B,切点分别为M、N,如图2,则
(1)四边形OMPN为平行四边形;
(2)切线PA与PB的斜率之积为定值;
(3)四边形OMPN的面积为定值;
(4)A、O、B三点共线.
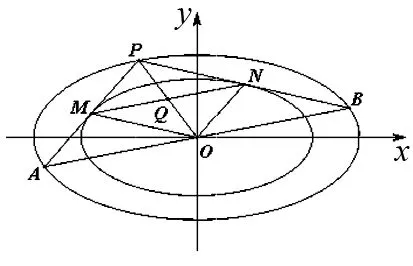
图2
证明:设P(x0,y0),M(x1,y1),N(x2,y2),
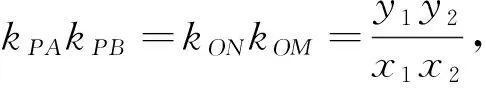
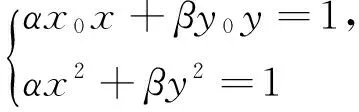
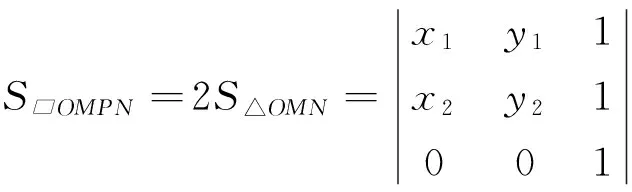

(4)连结OA、OB,由定理知PM=MA,PN=NB,又由(1)知MN平分PO,所以MN∥AO且MN∥OB,所以A、O、B三点共线.
二、相似比λ=2的相似椭圆性质
对于相似比为2的相似椭圆,除了相似椭圆共有的性质之外,还有如下性质.
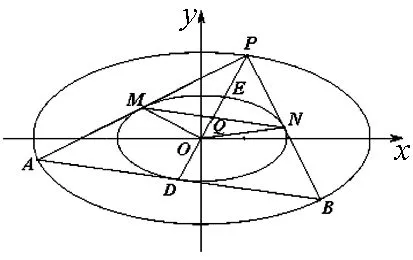
图3
命题2相似椭圆C1:αx2+βy2=1(α>0,β>0且α≠β)和C2:αx2+βy2=4,过C2上一点P作C1的两条切线,交椭圆C2分别为A、B,切点分别为M、N,如图3,则(1)AB是椭圆C1的切线;(2)△PAB的面积为定值.
证明:设P(x0,y0),M(x1,y1),N(x2,y2),
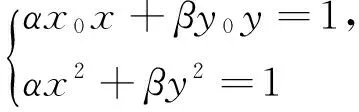

=1,所以AB切椭圆C1于点D.
(2)由(1)可得S△PAB=4S△PMN,又OQ∶OP=1∶4,所以S△PMN=3S△OMN,所以S△PAB=12S△OMN.而
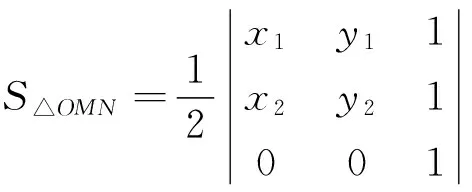
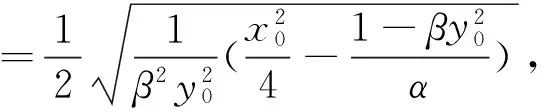
经过探究,笔者还发现上述三个椭圆之间存在如下关系
命题3过椭圆C1:αx2+βy2=1(α>0,β>0且α≠β)上一点M作切线,交椭圆C2:αx2+βy2=2于A、B两点,如图4,椭圆C2在A、B两点处的切线交于点P,则点P的轨迹是椭圆αx2+βy2=4.

图4
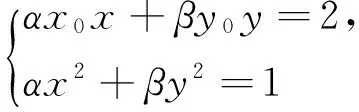
经历以上探究过程,不仅得出这两组特殊相似椭圆的优美性质,为进一步研究相似椭圆奠定了基础,还凸显了椭圆方程αx2+βy2=1在论证过程中所起的简便作用.
