非线性需求下四寡头价格博弈模型及其复杂特性

刘 峰,李亚光*,王宏兴

(1.合肥工业大学经济学院,安徽合肥230601; 2.合肥工业大学工业信息研究院,安徽合肥230601; 3.淮南师范学院金融学院,安徽淮南232038)

非线性需求下四寡头价格博弈模型及其复杂特性

刘 峰1,2,李亚光1,2*,王宏兴3

(1.合肥工业大学经济学院,安徽合肥230601; 2.合肥工业大学工业信息研究院,安徽合肥230601; 3.淮南师范学院金融学院,安徽淮南232038)

针对实际竞争环境,建立寡头厂商成本相异和广义非线性需求的四寡头价格博弈模型.基于厂商采用不同决策规则的假设,利用复杂动力学原理,给出了价格博弈模型纳什均衡解.研究了系统稳定、倍周期分叉以及混沌的复杂特性,探讨了价格调整速度和初始条件对该离散系统动态演化过程的影响,以此为基础研究了寡头厂商的价格决策.研究结果表明,寡头厂商都应采用较低的价格调整速度,慎重选择博弈的初始条件.当现任寡头厂商迅速调整价格阻止新厂商进入,使得市场陷入混乱时,运用反馈控制方法可实现混沌控制.

价格博弈;非线性需求;复杂性;不同价格决策;混沌控制

1 引 言

随着经济不断发展,在保险、电力、房地产、通信以及能源等行业中,市场往往被几个寡头厂商占领,寡头垄断成为一种普遍存在的市场形态.法国经济学家Bertrand在Cournot双寡头垄断模型基础上提出了以价格作为竞争手段的Bertrand模型.Bertrand模型假设消费者会选择价格较低的产品,寡头厂商会通过不断降价来争取更多的顾客;同时每个寡头厂商希望所获利润尽可能大,相互削价直至厂商的价格等于各自的边际成本.Agiza等[1-3]通过对三寡头动态博弈的时间演化的离散动态系统进行建模,考虑有限理性的因素,对多寡头博弈模型稳定性区域做了研究,结果表明混沌现象存在.同时,现实厂商博弈这一问题也引起了学者们的关注.Ahmed等[4]构建广告竞争模型,根据Lyapunov指数的变化分析复杂动力学行为;赖纯见等[5]通过对房地产寡头完全静态博弈分析,得出现实中纳什均衡可在有限理性不完全信息动态重复博弈下实现的结论;李榆等[6]运用纳什协商模型分析了电信运营商和服务提供商的博弈.在研究厂商博弈这一问题的过程中,探讨了厂商的生产成本和决策规则.现实中各寡头厂商的生产成本是不相同的,Bisch等[7,8]对具有线性成本函数的双寡头博弈模型进行研究;张骥骧等[9]指出寡头厂商不局限于线性且结构相同的成本函数,存在不同结构成本函数的双寡头博弈情况;易余胤等[10]提出非线性成本函数下双寡头重复博弈模型;在多组博弈中,陈曙等[11]将非线性成本函数引入到模型中,建立了基于有限理性的多组动态Cournot模型.当寡头厂商不再采用单一有限理性的决策规则,而是采用不同的决策规则时,潘玉荣等[12]提出不同理性双寡头博弈模型;方志耕等[13]构建了一种具有普遍适用性的描述性博弈结构模型;马军海等[14]采用延迟有限理性预期规则研究三寡头价格博弈模型的稳定性以及分岔、混沌等复杂性态.

文献[15–19]对价格博弈模型的稳定性以及分岔、混沌的影响因素进行了研究.Ma等[15,16]分别建立基于有限理性的混合双寡头模型和不同决策规则下的三寡头模型,发现价格调整速度变化会导致混沌,但是混沌控制策略使得市场有序竞争.Elsadany[17]指出当双寡头Cournot模型的反需求函数为非线性函数时,参数的变化也会引起混沌现象.从现有研究结果可看出,众多行业领域的市场结构呈现出采用价格竞争的四寡头垄断厂商的形式.马军海等[18]基于延迟有限理性决策,研究了中国啤酒市场线性需求的四寡头价格博弈模型,分析了系统的稳定性.Zhang等[19]构建中国保险市场的四维离散动态系统,研究表明在线性需求条件下,系统对价格调整速度和初始条件的敏感依赖.

文献[18,19]基于四维复杂离散动态模型探讨四寡头垄断厂商的内在复杂性,并对其进行混沌控制研究,说明四寡头垄断厂商在现实经济中普遍存在.但是当前在研究四寡头厂商行为时,所假设的需求函数是线性的,而现实中很多情况下需求函数是比较复杂的,非线性函数往往能够更准确的描述市场需求关系.同时在实际经济环境中,寡头厂商并不局限于结构相同的成本函数[7-11],寡头间或存在相异成本.本文在考虑寡头间存在相异成本、非线性市场需求函数的基础上,建立四寡头价格博弈模型,并探讨价格调整速度对寡头厂商利润的影响,以及价格博弈动力系统对初始条件的敏感依赖;同时利用MATLAB进行数值仿真,分析系统的复杂特性;最后使用延迟反馈控制法[20-22]控制混沌现象,其结果对中国石油行业可能存在的四寡头垄断市场管理决策提供理论依据.

2 价格博弈模型

在一定的预算约束下实现效用最大化时,可得出厂商的需求函数,效用函数的形式决定了需求函数的形式.新进寡头厂商可能由于创新技术与市场决策等因素,导致其产品相较与原寡头厂商存在显著差异,消费者更偏好此类产品,故需求函数形式不同.实际上,各厂商的生产成本也是不相同的,同类厂商的生产成本非常相近,而异类厂商的生产成本存在差异.为了研究问题的方便,在建立价格博弈模型时,给出以下假设:

1)市场上已有三个生产可替代产品的寡头厂商1,2,3,一个新进寡头厂商4进入市场,成为市场中新的强有力竞争者;

2)寡头厂商1,2,3的需求量与价格的关系满足二次多项式形式,即其需求函数是二次多项式;

3)原寡头厂商1,2,3属于同类寡头,其需求无显著差异,而新进寡头厂商4属于异类寡头,与原寡头厂商1,2,3相比,其需求存在较明显的差异,寡头厂商4的需求函数是线性的1例如,目前中国有中国石油天然气股份有限公司、中国石油化工集团公司和中国海洋石油总公司三大石油行业油气生产和销售厂商,随着国家市场经济的进一步深化,可能会有新的生产和销售厂商进入,这样就会形成四寡头竞争的新格局.在一般情况下,商品价格上升,需求量就会下降.因此需求函数是一个关于价格的单调减函数.同时,需求函数不是固定不变的,它会随着市场变化而变化.文献[18,19]假定需求函数是线性的,而文献[16]假定需求函数是非线性的.本文假定原寡头厂商1,2,3的需求函数为非线性函数,寡头厂商4的需求函数为线性函数.;

4)寡头厂商1,2,3的产品成本是关于需求量的函数,而需求量又是关于价格的函数,故寡头厂商1,2,3的成本是关于价格的函数,即一定区域、一定时期内产品成本仅由厂商市场价格决定,不受其它因素的影响;

5)寡头厂商4的成本与需求量呈正相关,成本函数是线性的.

一个寡头厂商不仅影响自己的决策,而且影响其他寡头厂商的决策,甚至改变整个市场的运行状态.根据假设2)和3),第t期寡头厂商1,2,3的非线性需求函数可设为

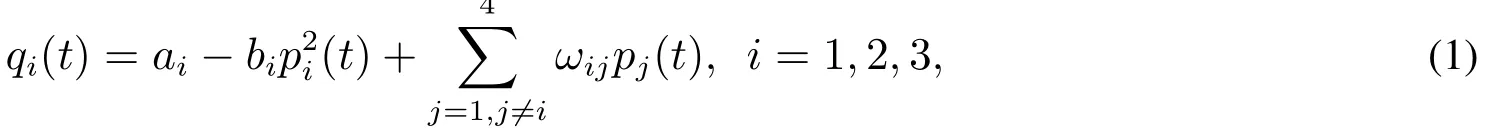
其中bi是需求对自身价格的弹性系数,ai,ωij,i/=j,j=1,2,3,4,为各寡头产品的相互替代率,pi和qi分别是第i个厂商的销售价格和需求量,i=1,2,3.

由假设4),可设成本函数形式为cipi(t),其中ci为厂商技术水平对价格的敏感系数,i=1,2,3.则寡头厂商1,2,3的利润函数表达式为

整理可得

新进寡头厂商和原寡头厂商生产的产品不完全同质,价格需求关系不同,需求函数结构存在差异.新进寡头厂商生产的产品比原寡头厂商的可替代性差,即使销售价格稍高,由于品牌效应、产品高品质与先进技术,仍然会有相对较高的需求.根据假设3),寡头厂商4的需求函数可设为

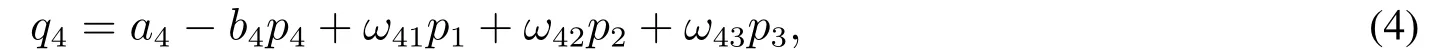
根据假设5),成本函数为c4q4(t),其中c4为单位产量的成本,则利润函数

2.1 四寡头价格博弈模型

由于寡头垄断市场信息的不完全性,每个厂商掌握的信息并不充分,只可能做出有限理性决策.考虑到厂商1,2,3是先进厂商,管理市场的经验比较丰富、处理市场信息能力比较强,采用有限理性决策规则[9,10,13,15].由于厂商4是新进厂商,往往只能是简单理性的,不具有足够的价格调整能力,故选择根据边际利润为零的最优反应价格决策原则.

在现实中厂商之间的博弈是一个动态过程,具有适应性和长程记忆性等特征,所以不妨假设厂商1,2,3采用有限理性决策规则,即第t+1期的价格决策由其第t期的价格与边际利润加权决定.厂商1,2,3采用有限理性决策规则进行决策,也就是说如果边际利润为正,需求量将在下一期增加,反之,则会减少.αi,i=1,2,3为价格调整速度,价格调整过程为

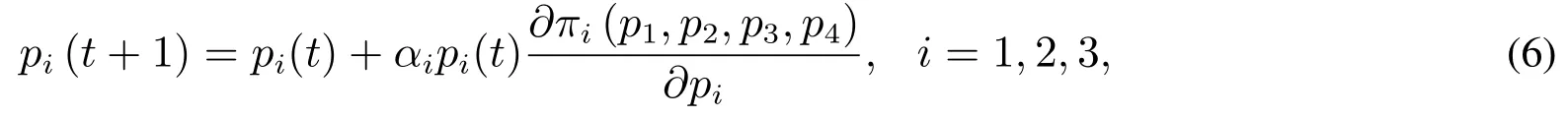
其中pi(t+1)和pi(t)分别是第t+1期和第t期的价格.在第t期,原寡头厂商的边际利润函数为

新进寡头厂商4在大部分情况下不完全了解市场信息,没有足够的价格调整能力,为了追求利润最大化,按照自身的边际利润来调整价格,选择根据自身边际利润的最优反应价格决策原则,即其下期的价格是基于本期对其他厂商价格的最优反应.现期价格仅仅通过第t期的最优价格决策决定,当

时,可得

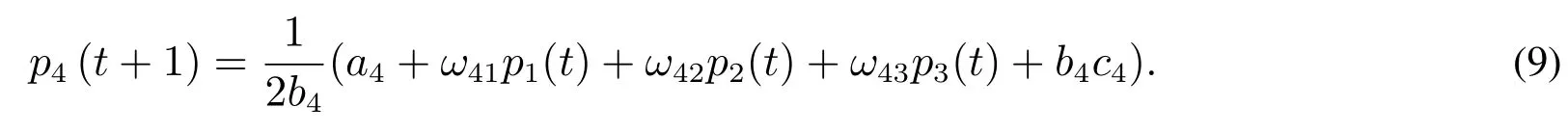
所以四个寡头厂商根据不同决策规则,形成的价格博弈离散动力学系统为

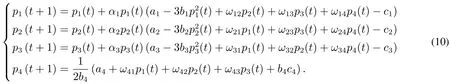
2.2 模型分析

根据四个寡头厂商建立的价格博弈离散动力学系统(10),研究其纳什均衡的局部稳定性,进而研究其博弈过程.令pi(t+1)=pi(t),i=1,2,3,4,求得系统平衡点.

为了讨论离散动力学系统(10)的稳定性,考虑其Jacobi矩阵为

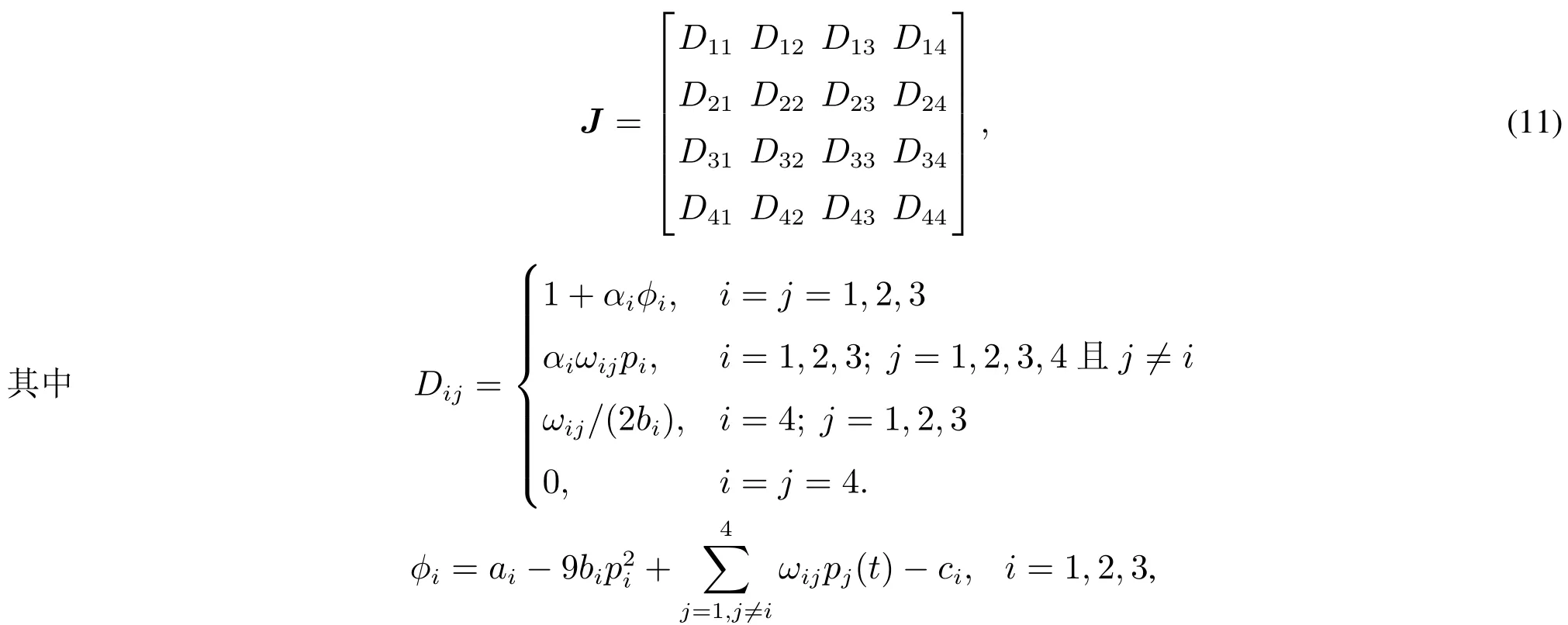
系统(10)的特征多项式为

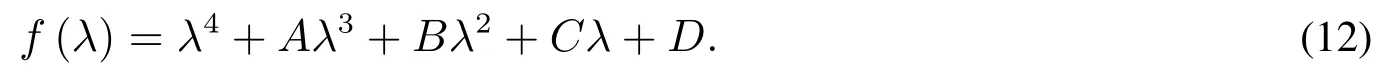
平衡点局部稳定的Jury条件是

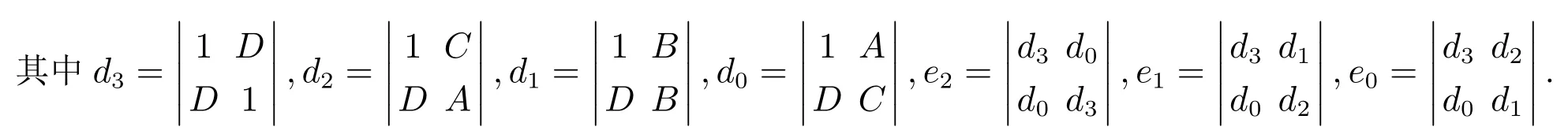
从经济管理学的角度看,系统的纳什均衡点比边界平衡点更具有现实意义,在该点处四个厂商的产量均不为0.通过计算特征值来判断纳什均衡点的稳定性很难,可以用Jury条件来判断纳什均衡点的稳定性,根据Jury条件得出的厂商价格调整速度α1,α2,α3的范围.在现实中,寡头厂商保证价格调整速度αi,i=1,2,3在此范围内,经过博弈将逐渐稳定到纳什均衡点,避免由于价格的过度调整引起市场混乱、利润降低.寡头企业管理者为了维持市场稳定,避免利润降低,更愿意保持在纳什均衡状态.

3 数值模拟分析

αi,i=1,2,3是可控参数,取下列参数值研究系统的均衡点及稳定性.对于四个寡头厂商的相互替代率ai,i=1,2,3,4,异类寡头4与原寡头厂商相比,产品差异性更大,对市场的操纵能力更强,产品可替代性较低,故设定需求函数中相互替代率a4相对较小.因为原寡头厂商的技术水平类似,设定考虑厂商技术水平条件下对价格的敏感系数ci,i=1,2,3较为接近,且均比新进厂商单位成本c4高.各寡头产品的相互替代率ωij参考中国保险市场数据[19],均设定在0和1之间,即

令pi(t+1)=pi(t),i=1,2,3,4,求得系统(10)平衡点

根据Jacobi矩阵J,求出每一点对应的特征值.有界均衡点E1,E2,E3,E4,E5,E6,E7的非零特征值均大于1,均是不稳定均衡点.E8的非零特征值均小于1,是系统(10)唯一的纳什均衡点.

考虑上述参数值时,纳什均衡点为E8=(0.931 8,0.957 9,0.980 9,0.940 6),Jacobi矩阵为

系统(10)的特征多项式

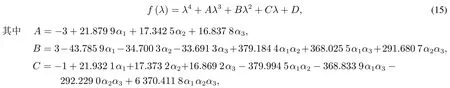
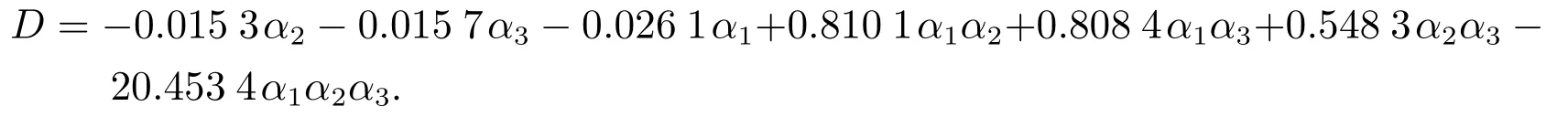
用纳什均衡点的Jury条件(13)验证可控参数αi,i=1,2,3的取值.当价格调整速度αi,i=1,2,3取值在一定范围内时,无论垄断厂商1,2,3最初如何定价,四个垄断厂商在纳什均衡点均会达到稳定.当价格调整速度αi,i=1,2,3取值超出一定范围,系统(10)纳什均衡点E8的稳定状态将会被打破,先出现分叉,随后出现混沌.

3.1 分叉与混沌仿真

根据Jury条件选取α2=0.07,α3=0.11时,得到四个寡头厂商随着α1变化的价格分叉图1;选取α1=0.12,α3=0.11时,得到四个寡头厂商随着α2变化的价格分叉图2;选取α1=0.12,α2=0.11时,得到四个寡头厂商随着α3变化的价格分叉图3.

图1,图2和图3分别出现了稳定周期、倍周期分叉以及混沌状态,随着α1,α2和α3的变化,价格也呈现动态变化过程.当α1,α2和α3达到某个临界点时,系统(10)由稳定状态变为分叉,再由分叉变为混沌.

根据判断系统状态的最大Lyapunov指数,得到系统最大Lyapunov指数变化图4,图5和图6.αi,i= 1,2,3不同,最大Lyapunov指数不同,稳定状态时Lyapunov指数小于0,混沌状态时大于0.

图1 α2=0.07,α3=0.11,α1变化的价格分叉图Fig.1 The price bifurcation with change of α1when α2=0.07,α3=0.11

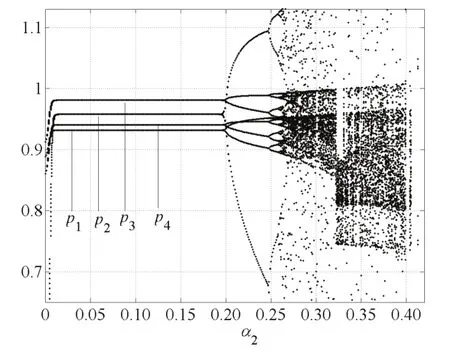
图2 α1=0.12,α3=0.11,α2变化的价格分叉图Fig.2 The price bifurcation with change of α2when α1=0.12,α3=0.11

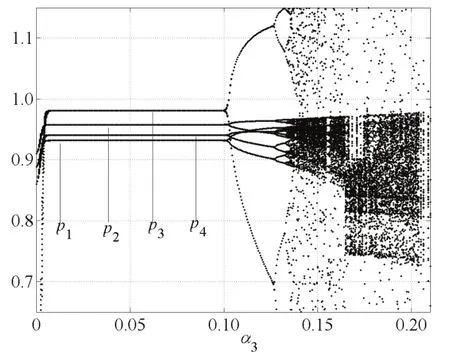
图3 α1=0.12,α2=0.11,α3变化的价格分叉图Fig.3 The price bifurcation with change of α3when α1=0.12,α2=0.11

图4 当α2=0.07,α3=0.11时,α1的系统最大Lyapunov指数(L)动态变化图Fig.4 Change of the maximal Lyapunov exponent with α1when α2=0.07,α3=0.11

图5 当α1=0.12,α3=0.11时,α2的系统最大Lyapunov指数(L)动态变化图Fig.5 Change of the maximal Lyapunov exponent with α2when α1=0.12,α3=0.11

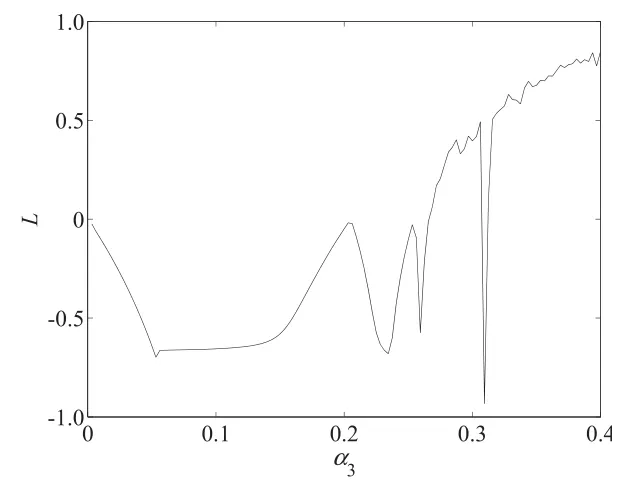
图6 当α1=0.12,α2=0.11时,α3的系统最大Lyapunov指数(L)动态变化图Fig.6 Change of the maximal Lyapunov exponent with α3when α1=0.12,α2=0.11

当α2=0.07,α3=0.11时,垄断厂商1的价格调整速度α1为变量.由图1,图4知,当0＜α1＜0.155时,Lyapunov指数小于0,此时系统(10)为稳定状态;当α1=0.155时,系统(10)出现第一次分叉,Lyapunov指数等于0;当α1=0.198时,系统出现第二次分叉,Lyapunov指数等于0,则0.155＜α1＜ 0.198是周期2轨道分叉区域;当α1=0.209时,系统出现第四次分叉,Lyapunov指数等于0,则0.198＜α1＜0.209是周期4轨道分叉区域;当α1＞0.209时,系统进入混沌状态,Lyapunov指数大于0,进一步价格调整将引起市场混乱.在分叉图的空白区域,α1=0.254附近Lyapunov指数小于0.

由图2和图5知,当α1=0.12,α3=0.11时,随着α2变化,当α2=0.197时,系统出现倍周期分叉;α2＞0.268时,系统进入混沌状态.由图3和图6知,当α1=0.12,α2=0.11时,随着α3变化,当α2=0.202时,系统出现倍周期分叉;当α1＞0.273时,系统进入混沌状态,进一步价格调整将引起市场混乱.

混沌发生时市场陷入混乱无序状态,无论是厂商自身还是其竞争对手都会受到伤害.各寡头厂商管理者尽力控制价格调整速度,避免因价格战所带来的市场混乱.复杂动力系统的混沌研究为宏观调控提供一定依据.

3.2 初值条件影响系统动态演化过程

当α1=0.31,α2=0.32,α3=0.35时系统处于混沌状态.从纳什均衡点E8开始,价格随时间无序变化.为了探究初始条件的变化对系统演化的混沌状态的影响,在图7中分别以纳什均衡点E8= (0.931 8,0957 9,0.980 9,0.940 6)为初始值和相对E8有微小变动的初始值Fi画出了寡头厂商i的产品价格pi随时间变化的曲线,i=1,2,3,4.与四个寡头厂商相应的Fi(加下划线的数据表示相对E8有微小变动)取值如下:

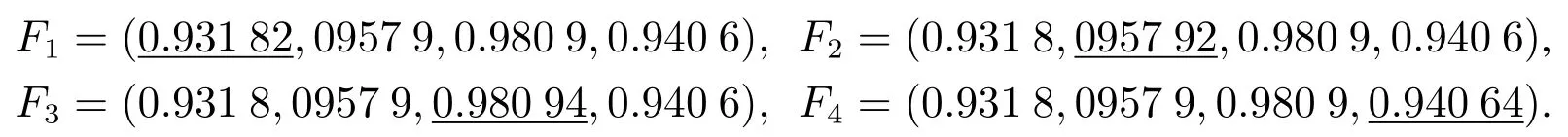
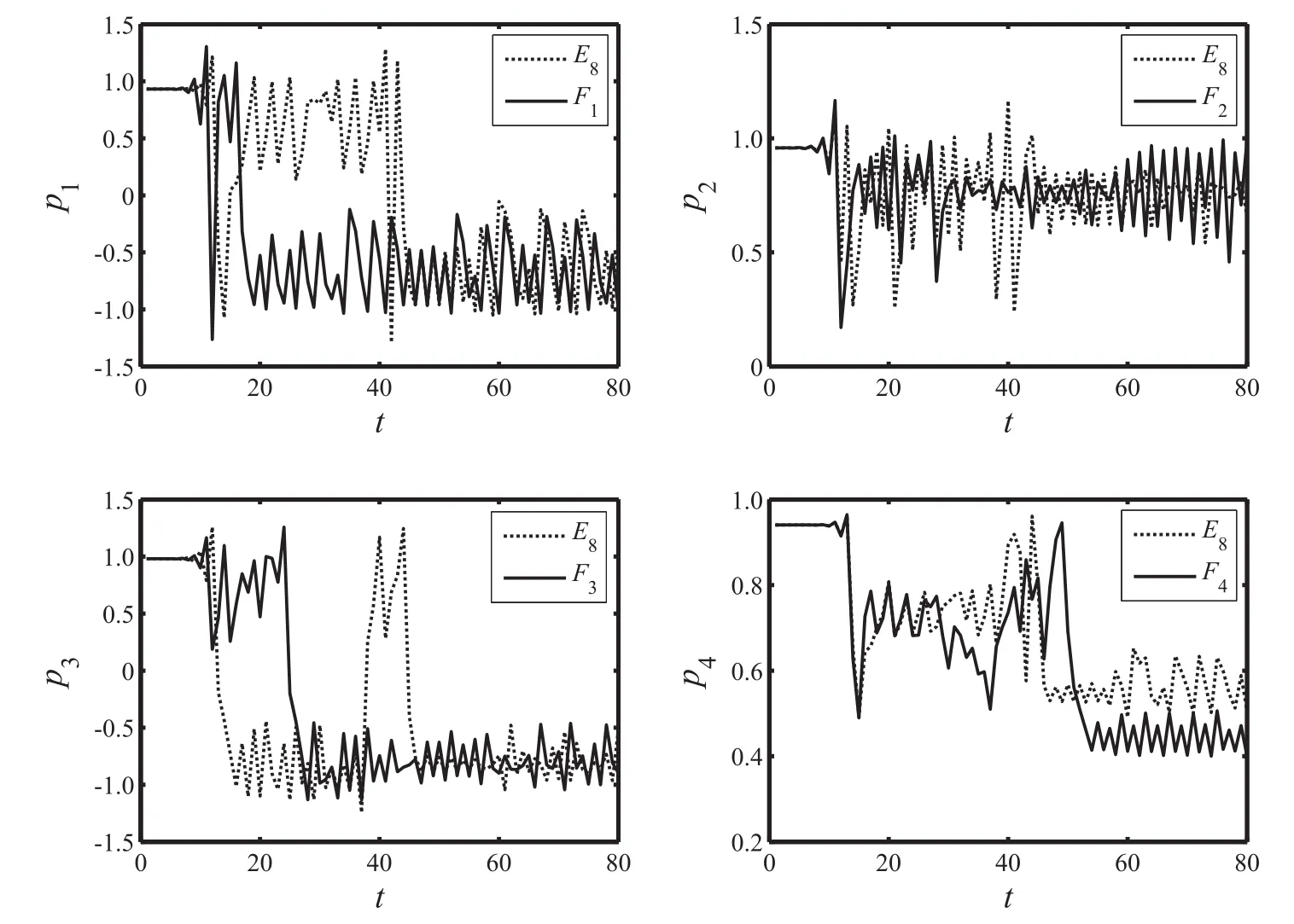
图7 初始条件变化时,四寡头厂商价格随时间变化对比图Fig.7 Price difference changes of four oligarchs with time when initial conditions change

图7表明,与E8,Fi对应的两条曲线在系统动态演化的前期均是无序状态且无显著差别,但随着时间增加,价格变动轨迹的区别越来越明显.以均衡点E8为初值的价格随时间变化较为平稳,振荡幅度较小,而以Fi为初值的价格变化轨迹却有较大幅度的振荡.由此可知系统动态演化过程的混沌现象对初始条件变化较敏感.

3.3 价格调整速度影响利润

图8,图9和图10是α1,α2,α3变化时的利润分叉图.α1,α2,α3选取与分叉图相同的参数,四个寡头厂商利润分岔图中的稳定、周期2轨道分叉、周期4轨道分叉和混沌区域与图1,图2,图3的价格分叉图中出现的稳定周期、倍周期分叉以及混沌区域相同.

同理,α2,α3的变化对厂商2,3的利润具有类似的影响.

由图11知,当价格调整速度α1较小,厂商利润不断增加,直至Lyapunov指数为0,利润开始下降,这也得出价格调整速度不能过快的结论.由图8,图11可以看出,当0＜α1＜0.155时,系统处于稳定状态,四寡头厂商的利润平稳变化;当0.155＜α1＜0.198时,系统处于倍周期分叉状态,四寡头厂商的利润下降;当0.198＜α1＜0.209时,系统处于四倍周期分叉状态,四寡头厂商的利润继续下降;当α1＞0.209时,系统处于混沌状态,四寡头厂商的利润较低.在相同参数条件下,四个寡头厂商的利润分岔图与价格分叉图比较,发现系统的稳定周期、倍周期分叉以及混沌状态相同,由此得出价格调整速度对于价格与利润产生一样的影响.所以,寡头企业管理者可以仅仅根据价格分叉图来尽力避免分叉、混沌现象的产生,以确保利润最大化.

图8 α2=0.07,α3=0.11,α1变化的利润分叉图Fig.8 The proft bifurcation with change of α1when α2=0.07,α3=0.11

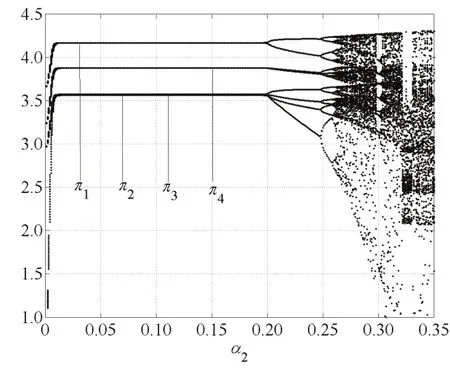
图9 α1=0.12,α3=0.11,α2变化的利润分叉图Fig.9 The proft bifurcation with change of α2when α1=0.12,α3=0.11

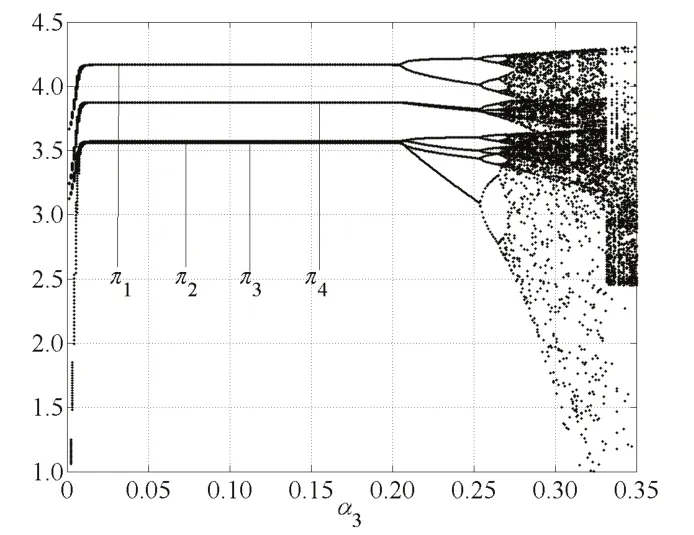
图10 α1=0.12,α2=0.11,α3变化的利润分叉图Fig.10 The proft bifurcation with change of α3when α1=0.12,α2=0.11

图11 α1变化时利润图Fig.11 The proft with the change of α1

4 混沌控制

一般情况下,现任寡头厂商为阻止新厂商进入市场会采取价格战,而迅速调整的价格使市场陷入混沌状态中.并且参数的微小变化可能会使得系统由稳定状态陷入混沌.所以,现任寡头厂商1,2,3与新进寡头厂商4的市场稳定状态可能是暂时和短期的.当市场处于混沌状态时,每个厂商的价格是不确定的,厂商无法实现最大化利润.因此每个厂商都希望控制混沌现象,促使稳定状态的形成.

本文使用延迟反馈控制法[14,17,18]控制混沌,依据系统的具体参数取值,只有原厂商1,2,3引入延迟变量[14],才可以达到理想效果,故采用此方法对系统(10)实施控制.控制系统如下

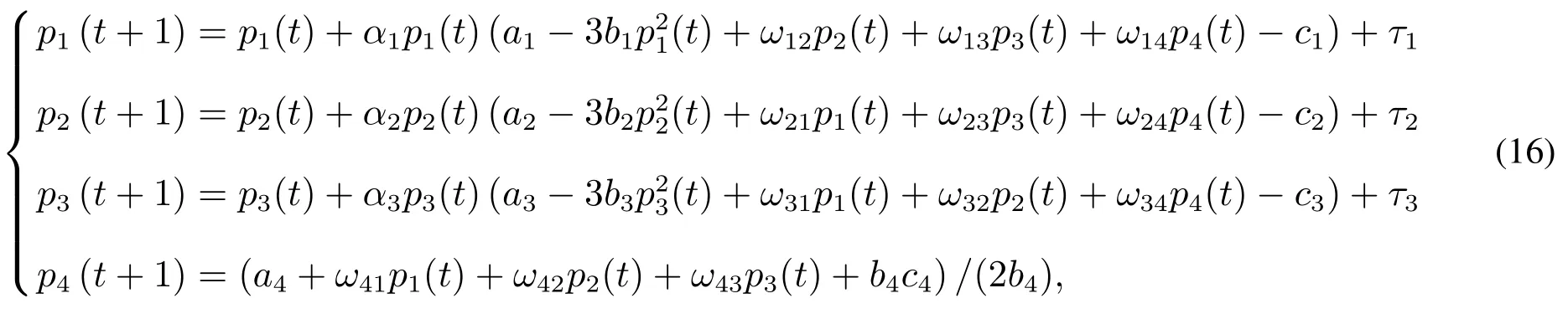
其中控制信号为τi=K(pi(t+1-T)-pi(t+1)),i=1,2,3,控制因子为K,输出信号延迟时间长度为T,取T=1.

图12描述了控制因子K对价格的影响.图12表明,当0＜K＜0.504时,系统处于混沌状态;当0.504＜K＜0.576时,系统处于周期4轨道分叉状态;当0.576＜K＜0.892时,系统处于周期2轨道分叉状态;当K＞0.892时,系统处于稳定状态,控制了混沌,厂商可以实现利润最大化.

图12 控制因子K对价格的影响Fig.12 The infuence of K on the price

5 结束语

当一个新寡头厂商进入三个寡头厂商占领的市场时,通过对不同决策规则下具有相异成本和非线性需求函数的寡头厂商价格博弈过程的分析,提出了一个新的四维离散动力学系统,建立了四寡头价格博弈模型.寡头厂商为了追求自身利益最大化,会不断加快自己的价格调整速度,忽视其对整个市场的外部效应,数值模拟结果表明,一旦价格调整速度超出稳定范围会使整个市场陷入混沌,此时自身利润反而降低.无论是新进入的寡头厂商还是现任寡头厂商,基于利益最大化的目的都应采用较低的价格调整速度.当市场中寡头厂商价格调整速度过快时,会出现分叉甚至混沌的不和谐现象,政府应及时出台相关政策来调控市场,使市场健康有序的发展.

所有寡头厂商初始状态的微小差别都会对博弈结果产生极大影响,为使市场处于稳定状态,寡头厂商应慎重选择博弈的初始条件.市场陷入混乱时,寡头厂商可采用延迟反馈控制法控制混沌,达到抢占更多市场份额并且挤压对手的生存发展空间的目的.本文在建立博弈模型时,假定厂商销售量只与价格有关系,实际上影响销售量的因素很多,例如产品质量、市场需求等,这些问题有待进一步分析研究.

参考文献:

[1]Agiza H N,Bischi G I,Kopel M.Multistability in a dynamic Cournot game with three oligopolists.Mathematics and Computers in Simulation,1999,51(1/2):63–90.

[2]Agiza H N,Hegazi A S,Elsadany A A.The dynamics of Bowley’s model with bounded rationality.Chaos,Solitons&Fractals, 2001,12(9):1705–1717.

[3]Agiza H N,Elsadany A A.Chaotic dynamics in nonlinear duopoly game with heterogeneous players.Chaos,Solitons&Fractals, 2004,149(3):843–860.

[4]Ahmed E,Agiza H N,Hassan S Z.On modelling advertisement in Cournot duopoly.Chaos,Solitons&Fractals,1999,10(7): 1179–1184.

[5]赖纯见,陈 迅.房地产寡头有限理性博弈模型的复杂性分析.系统工程学报,2013,28(3):285–296. Lai C J,Chen X.Analysis of a game with bounded rationality in oligopoly market.Journal of Systems Engineering,2013,28(3): 285–296.(in Chinese)

[6]李 榆,吴军口,冯艳刚.基于Nash协商模型的电信增值服务供应链研.系统工程学报,2014,29(6):824–832. Li Y,Wu J K,Feng Y G.Research on telecom value-added service chain based on Nash bargaining model.Journal of Systems Engineering,2014,29(6):824–832.(in Chinese)

[7]Bischi G I,KopelM,HassanS Z.Equilibrium selection in anonlinearduopoly gamewith adaptiveexpectations.JournalofEconomic Behavior&Organization,2001,46(1):73–100.

[8]Bischi G I,Mammana C,Gardini L.Multistability and cyclic attractors in duopoly games.Chaos,Solitons&Fractals,2000,11(4): 543–564.

[9]张骥骧,达庆利,王延华.寡占市场中有限理性博弈模型分析.中国管理科学,2006,14(5):109–113. Zhang J X,Da Q L,Wang Y H.Analysis of a game with bounded rationality in oligopoly market.Chinese Journal of Management Science,2006,14(5):109–113.(in Chinese)

[10]易余胤,盛昭瀚,肖条军.具溢出效应的有限理性双寡头博弈的动态演化.系统工程学报,2004,19(3):244–250. Yi Y Y,Sheng Z H,Xiao T J.Dynamics of duopoly model with bounded rationality and spillover effect.Journal of Systems Engineering,2007,4(2):71–76.(in Chinese)

[11]陈 曙,姚洪兴.多组动态古诺模型的稳定性分析.复杂系统与复杂性科学,2006,3(3):48–55. Chen S,Yao H X.Stability analysis for a dynamical multi-team Cournot game.Journal of Systems Engineering,2006,3(3):48–55. (in Chinese)

[12]潘玉荣,贾朝勇.不同理性双寡头博弈模型的复杂性分析.复杂系统与复杂性科学,2007,4(2):71–76. Pan Y R,Jia C Y.Complex dynamics analysis for a duopoly game with heterogeneous plyers.Complex Systems and Complexity Science,2007,4(2):71–76.(in Chinese)

[13]方志耕,刘思峰,李元年,等.基于有限知识和理性的双寡头战略定产纳什均衡问题研究.中国管理科学,2006,14(5):114–120. Fang Z G,Liu S F,Li Y N,et al.Study on the Nash equilibrium of duopoly strategy output-making based on bounded knowledge and bounded rationality.Chinese Journal of Management Science,2006,14(5):114–120.(in Chinese)

[14]马军海,彭 靖.延迟决策对一类寡头博弈模型的影响分析.系统工程学报,2010,25(6):812–817. MA J H,Peng J.Infuence of delayed decision on an oligopoly game model.Journal of Systems Engineering,2010,25(6):812–817. (in Chinese)

[15]Ma J,Pu X.The research on Cournot-Bertrand duopoly model with heterogeneous goods and its complex characteristics.Nonlinear Dynamics,2013,72(4):895–903.

[16]Ma J,Sun Z.The research on price game model and its complex characteristics of triopoly in different decision-making rule. Nonlinear Dynamics,2013,71(1/2):35–53.

[17]Elsadany A A.A dynamic Cournot duopoly model with different strategies.Journal of the Egyptian Mathematical Society,doi: 10.1016/j.joems.2014.01.006.

[18]马军海,吴可菲.中国啤酒市场的四寡头价格博弈及其延迟决策.系统工程学报,2013,28(6):717–728. Ma J H,Wu K F.Four-oligarchy price game and its delayed decision in Chinese beer market.Journal of Systems Engineering,2013, 28(6):717–728.(in Chinese)

[19]Zhang J,Ma J.Research on the price game model for four oligarchs with different decision rules and its chaos control.Nonlinear Dynamics,2012,70(1):323–334.

[20]Wu W,Chen Z,Ip W H.Complex nonlinear dynamics and controlling chaos in a Cournot duopoly economic model.Nonlinear Analysis:Real World Application,2010,11(5):4363–4377.

[21]张建雄,唐万生.一类Holder连续的混沌系统分析和控制.系统工程学报,2010,25(6):829–834. Zhang J X,Tang W S.Analysis and control for a class of chaotic systems with Holder continuity.Journal of Systems Engineering, 2010,25(6):829–834.(in Chinese)

[22]Fuh C C,Tsai H H,Yao W H.Combining a feedback linearization controller with a disturbance observer to control a chaotic system under external excitation.Communications in Nonlinear Science&Numerical Simulation,2012,17(3):1423–1429.

Four oligarchs price game model and its complex characteristics with nonlinear demand

Liu Feng1,2,Li Yaguang1,2*,Wang Hongxing3
(1.School of Economics,Hefei University of Technology,Hefei 230601,China; 2.Research Center of Industry Information,Hefei University of Technology,Hefei 230601,China; 3.School of Finance,Huainan Normal University,Huainan 232038,China)

In view of the actual competitive environment a four-oligarch price game model with variable costs and general nonlinear demand is established.Based on the hypothesis that vendors use different decision rules, using complex principle of dynamics the Nash equilibrium solutions are give.This paper studies the complex characteristics such as stability,the period-doubling bifurcation,and chaos.It also discusses the effects of price adjustment speed and initial conditions on the movement of the dynamic system,and the price decisions of oligarchs.The results show that the lower price adjustment speed should be taken,and initial conditions of the game must be chosen carefully.When the current oligarchs quickly adjust price in order to prevent a new oligarch from entering and market into chaos results,the delay feedback control method can be used to control the chaos.

price game;nonlinear demand;complexity;different price decision;chaos control

TP273

A

1000-5781(2016)06-0719-10

10.13383/j.cnki.jse.2016.06.001

刘 峰(1971—),男,安徽天长人,博士生,副教授,硕士生导师,研究方向:区域经济学,Email:dwoffce@126.com;

2015-02-16;

2015-11-19.

国家自然科学基金资助项目(11401243);中央高校基本科研业务费专项资金资助项目(J2014HGXJ0156);安徽省人文社科重点研究基地资助项目(SK2015A159).

*通信作者

李亚光(1990—),女,安徽淮南人,硕士生,研究方向:区域经济学,博弈论,Email:yaguangli926@163.com;

王宏兴(1981—),男,安徽淮南人,博士,副教授,研究方向:数值计算,Email:winghongxing0902@163.com.