理解函数概念 突破复习难点

李月恬

函数是初中数学的核心知识，是中考命题的热点素材，因此要视为重中之重的复习内容.

一、突破难点

1.学会捕捉函数图像的信息.①横轴和纵轴表示的意义，单位长度是多少；②函数的增减性：沿横轴从左向右，开口向上时函数y随自变量x的增大（减小）而增大（减小），开口向下时函数y随自变量x的增大（减小）而减小（增大），图像与x轴平行时函数y的值不变；③函数的最值：图像位于某条与x轴平行的直线上（下）方时函数有最小（大）值，图像位于与x轴平行的两条直线之间时，函数既有最小值也有最大值.

2.理解函数与方程（组）、不等式（组）的联系.①方程的解：从函数的角度看是函数值为0时自变量的值，从图像的角度看是直线与横轴交点的横坐标；②方程组的解：从函数的角度看是两个函数解析式组成的方程组的解，从图像的角度看是两条直线交点的坐标；③不等式的解：当y>（<）0时，从函数的角度看是函数值大（小）于0时自变量允许值的集合，从图像的角度看是横轴上（下）方直线部分横坐标自变量的取值范围；④不等式组的解：当y1>（<）y2时，从函数的角度看是函数值y1>（<）y2时自变量允许值的集合，从图像的角度看是一条直线y1在另一条直线y2上（下）方的部分对应的横坐标的取值范围.

3.确定二次函数解析式.①已知抛物线上三点坐标时，可设一般式y=ax2+bx+c；②已知抛物线的顶点坐标或最值、对称轴时，可设顶点式y=a（x-h）2+k；③已知抛物线与横轴两交点的坐标时，可设交点式y=a（x-x1）（x-x2）.

二、关注解题中的易错点

1.求函数自变量的取值范围时，考虑不周全，顾此失彼.

2.忽视函数定义中的条件.如一次函数y=kx+b中的k≠0，x的次数为1；反比例函数y=[kx]中的k≠0，x的次数为-1；二次函数y=ax2+bx+c中的a不能为0，x的最高次数为2.

3.混淆点的坐标与线段长的关系.点到纵（横）轴的距离是对应点的横（纵）坐标的绝对值；反过来，点到纵（横）轴的距离表示点的坐标，要加上点所在象限的坐标符号，常常由于忽视分类讨论而造成漏解.

4.误求二次函数的最值.只有当顶点的横坐标在自变量的取值范围内时，顶点的纵坐标才是函数的最值，否则函数的最值在图像的端点处取得，或者没有最值.

三、典型问题解析

例1 （2016·山东威海）函数y=[x+2x]的自变量x的取值范围是（ ）.

A.x≥-2 B.x≥-2且x≠0

C.x≠0 D.x>0且x≠-2

【解析】由题意，得x+2≥0，且分母不为0，∴x≥-2且x≠0，故选择B.

【点评】自变量的取值范围既与函数的解析式有关，又与问题中的实际意义有关.一般来说，求函数自变量的取值范围要注意以下几点：（1）整式的取值范围是全体实数；（2）分式的分母不能为0；（3）偶次根式的被开方数不能是负数；（4）0指数或负指数幂的底数不能为0；（5）自变量的取值不能使实际问题失去意义.此外，要注意“或”与“且”的区别.

例2 （2016·四川宜宾）图1是甲、乙两车在某时段速度随时间变化的图像，下列结论错误的是（ ）.

A.乙前4秒行驶的路程为48米

B.在0到8秒内甲的速度增加4米/秒

C.两车到第三秒时行驶的路程相等

D.在4至8秒内甲的速度都大于乙的速度

【解析】由图知乙的整个行驶速度变化分两段，第一段（前4秒）图像与x轴平行，即时间改变，速度不变，都是12米/秒，所以前4秒行驶了48米；第二段（4-8秒），乙的图像都在甲的图像下面，说明4到8秒内甲的速度都大于乙的速度；再看图中甲的图像是一条过原点的直线段，说明速度随时间均匀变化，8秒内速度由0变到32，所以速度增加4米/秒.说明A、B、D都正确，故错误的是C，选C.

【点评】对于函数图像信息题，要充分挖掘图像所蕴含的信息，通过读图、想图、析图来寻找解题的突破口.

例3 （2016·河北）若k≠0，b<0，则y=kx+b的图像可能是（ ）.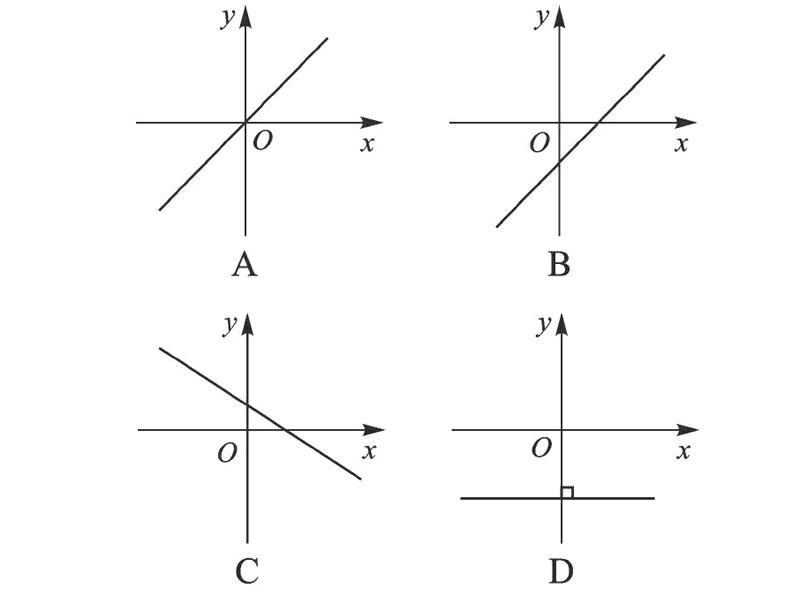

【解析】对于y=kx+b，当x=0时，y=b，即y=kx+b的图像与y轴的交点为（0，b），当b<0时，（0，b）在x轴下方，又因为k≠0，故选B.

【点评】对于含字母的函数图像识别问题，可运用推理的方法，也可借助特殊值来确定.

例4 （2016·重庆B卷）如图2，在平面直角坐标系中，一次函数的图像与反比例函数的图像交于第二、四象限内的A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是（m，-4），连接AO，AO=5，sin∠AOC=[35].

（1）求反比例函数的解析式；

（2）连接OB，求△AOB的面积.

【分析】（1）过点A作AE⊥x轴于点E，通过解直角三角形求出线段AE、OE的长度，得到点A的坐标，利用待定系数法可求出反比例函数解析式；（2）先求出点B的坐标，由点A、B的坐标可求出直线AB的解析式，令y=0即可求出点C的坐标，再利用三角形面积公式可求面积.

解：（1）过点A作AE⊥x轴于点E.设反比例函数解析式为y=[kx].∵AE⊥x轴，∴∠AEO=90°.在Rt△AEO中，AO=5，sin∠AOC=[35]，∴AE=AO

·sin∠AOC=3，OE=[AO2-AE2]=4，∴A（-4，3）.∵A（-4，3）在反比例函数y=[kx]的图像上，∴k

=-12.∴反比例函数解析式为y=[-12x].

（2）∵点B（m，-4）在反比例函数y=[-12x]的图像上，∴m=3，∴B（3，-4）.设直线AB的解析式为y=ax+b，将A（-4，3）、B（3，-4）代入y=ax+b中得：[3=-4a+b，-4=3a+b，]解得[a=-1，b=-1，]∴一次函数解析式为y=-x-1.令y=-x-1中y=0，则x=

-1，即C（-1，0），∴S△AOB=[12]OC·（yA-yB）=[12]×1×[3-（-4）]=[72].

【点评】像本例这类问题主要是求反比例函数、一次函数的解析式以及某三个点组成的三角形的面积.求三角形的面积时，通用方法如下：如图3，过点A作x轴的垂线l交BC于点D，则S△ABC=S△ABD+S△ACD=[12]·（yA-yD）·（xC-xB）.

例5 （2016·甘肃兰州）二次函数y=ax2+bx+c的图像如图4所示，对称轴是直线x=-1.有以下结论：①abc>0，②4ac2.其中正确的结论的个数是（ ）.

A.1 B.2 C.3 D.4

【解析】①由抛物线的开口向下可知a<0；由抛物线的对称轴在y轴左侧可知a、b同号，则b<0，且[-b2a]=-1；由抛物线与y轴的交点在y轴的正半轴上可知c>0.∵a<0，b<0，c>0，∴abc>0正确.

②∵抛物线与x轴有两个交点，∴b2-4ac>0，∴4ac

③∵抛物线对称轴是直线x=-1，∴[-b2a]=-1，∴2a-b=0，∴2a+b=0错误.

④由图像可知，当x=-1时，y>2，∴a-b+c>2正确，故选C.

【点评】解答有关二次函数图像问题，要抓住抛物线与x、y轴的交点，对称轴，顶点坐标，特殊点，常从二次函数图像性质出发，找出a、b、c的关系，再结合对称轴，确定a、b之间的关系，判断与x轴交点情况可利用判别式b2-4ac.

例6 （2016·湖北咸宁）某网店销售某款童装，每件售价60元，每星期可卖300件.为了促销，该店决定降价销售，市场调查反映：每降价1元，每星期可多卖30件.已知该款童装每件成本价40元.设该款童装每件售价x元，每星期的销售量为y件.

（1）求y与x之间的函数关系式；

（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润是多少？

（3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？

【分析】（1）由“每星期的销售量=原来的销售量+降价而多销售的销售量”可得函数关系式；（2）根据“销售量×（售价-进价）=利润”，构建二次函数求最大值；（3）列一元二次方程求出售价，再根据抛物线确定出每星期销售利润不低于6480元时x的取值范围，最后由一次函数的性质确定出每星期至少要销售该款童装的件数.

解：（1）y=300+30（60-x）=-30x+2100；

（2）设每星期的销售利润为W元，依题意，得W=（x-40）（-30x+2100）=-30（x-55）2+6750.∵a=-30<0，∴x=55时，W最大值=6750（元），即每件售价定为55元时，每星期的销售利润最大，最大利润是6750元；

（3）由题得-30（x-55）2+6750=6480，解得x1=52，x2=58.∵W=-30（x-55）2+6750的开口向下，∴当52≤x≤58时，每星期销售利润不低于6480元.在y=-30x+2100中，k=-30<0，y随x的增大而减小，∴当x=58时，y最小值为360.即每星期至少要销售该款童装360件.

【点评】利润=（售价-进价）×销售量.当销售量是售价的一次函数时，则利润是售价的二次函数.本题综合考查了一次函数、二次函数的应用.建立函数并运用一次函数和二次函数的性质解题是关键.

（作者单位：江苏省泰州市姜堰区实验初级中学）