曲线坐标系下三维弹性壳体中的微分几何关系

沈晓芹， 李昊明

(西安理工大学 理学院，陕西 西安 710054)



曲线坐标系下三维弹性壳体中的微分几何关系

沈晓芹， 李昊明

(西安理工大学 理学院，陕西 西安 710054)

本文建立了三维弹性壳体和其中性面上各点之间的某些微分几何关系表达式，它对形成二维线性、非线性弹性壳体模型非常重要。具体地，三维弹性体上各点的协变度量张量、逆变度量张量、度量张量矩阵的行列式以及Christoffel符号是由二维中性曲面上的微分几何表达式按壳体厚度方向的变量渐近展开来表示。

微分几何；度量张量；Christoffel符号

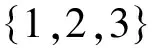
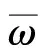
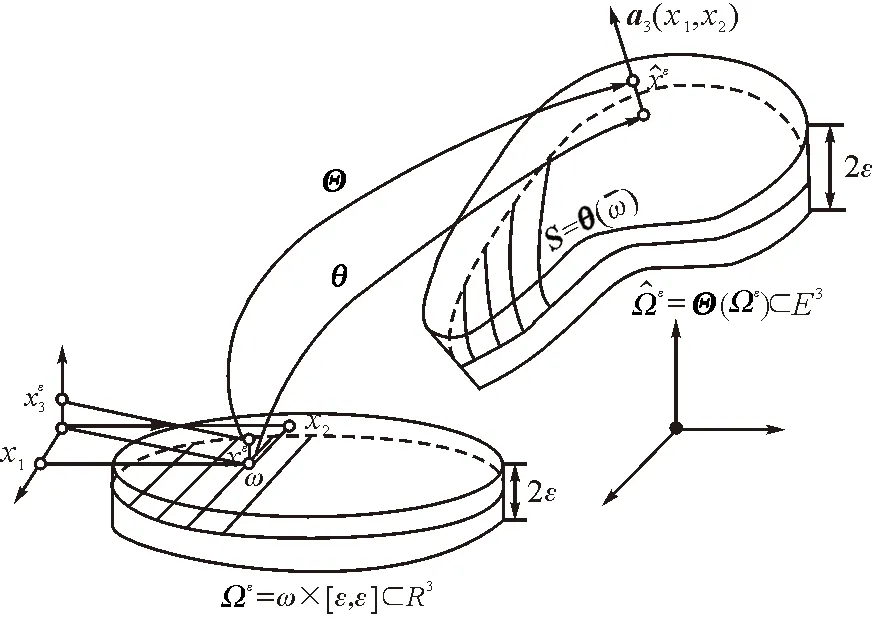
图 1 壳体ε及其中性面S[2]Fig.1 Shell εwith middle surface S[2]

(1)

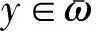
这些矢量ai(y)在点θ(y)处构成了协变基矢量，而矢量ai(y)定义为：

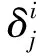
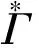
(2)

(3)

(4)

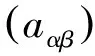
(5)

度量张量的行列式为:

在第二部分中，3D区域上的度量张量、度量矩阵的行列式和Christoffel符号可由2D曲面上表达式按壳体厚度方向的变量渐近展开来表示。

1 主要结论

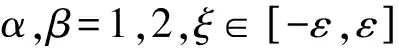
证明:

(6)

将式(1)～(4)代入(6)，基于bαβ的对称性，得到:

根据a3的定义，有

(8)

则:

因此:

(9)

将式(8)～(9)代入(7)，得

类似地:

gα3=0

g33=g3·g3=∂3Θ·∂3Θ=

0+0+0+a3·a3=1

证毕。

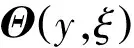
(10)

其中：

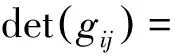
证明:

其中，

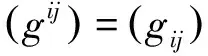
证毕。

(11)

其中α,β,σ=1,2。

证明：

(12)

由于a3·a3=1，有:

则:

(13)

将式(13)代入(12)，得：

类似地，

证毕。

(14)

其中α,β,σ=1,2。

证明：

由式(5)，有：

gστΓαβ,τ+gσ3Γαβ,3=gστΓαβ,τ

g31Γαβ,1+g32Γαβ,2+g33Γαβ,3=Γαβ,3

gστΓα3,τ+gσ3Γα3,3=gστΓα3,τ

gατΓ33,τ+gα3Γ33,3=0

g3τΓα3,τ+g33Γα3,3=Γα3,3=0

g3τΓ33,τ+g33Γ33,3=Γ33,3=0

因此，式(14)能够容易地从定理2和定理3而得到。

证毕。

[1]CIARLET P G. An introduction to differential geometry with applications to elasticity[M]. Heidelberg: Springer- Verlag, 2005.

[2]CIARLET P G. Mathematical Elasticity, Vol.III: Theory of Shells[M]. North-Holland, 2000.

[3]KOITER W T. A consistent first approximation in the general theory of thin elastic shells[C]//IUTAM Symposium on the Theory of Thin Elastic Shells, Amsterdam，August 1959 .

[4]KOITER W T. On the foundations of the linear theory of thin elastic shells[J]. Proc. Kon. Ned. Akad. Wetensch, 1970, B73: 169-195.

[5]LI Kaitai, SHEN Xiaoqin. A dimensional splitting method for linearly elastic shell[J]. International Journal of Computer Mathematics, 2007, 84(6): 807-824.

[6]SHEN Xiaoqin, LI Kaitai, MING Yang. Asymptotic expansions of stress tensor for linearly elastic shell[J]. Applied Mathematical Modelling, 2013, 37(16-17): 7964-7972.

[7]XIAO Liming. Justification of two-dimensional nonlinear dynamic shell equations of Koiter’s type[J]. Nonlinear Analysis, 2005, 62(3): 383-395.

(责任编辑 王绪迪，王卫勋)

Differential geometric relations on the three-dimensional elastic shell in the curvilinear ordinates systems

SHEN Xiaoqin， LI Haoming

(School of Sciences, Xi’an University of Technology, Xi’an 710054, China)

The differential geometric relations between 3D elastic shell and the middle surface of shell are provided, which is of importance for forming 2D linear and nonlinear elastic shell models. Concretely, the metric tensor, the determinant of metric matrix field and the Christoffel symbols on the 3D elasticity are expressed by those on the 2D middle surface, which are featured by the asymptotic expressions with respect to the variable in the direction of thickness of the shell.

differential geometry; metric tensor; Christoffel symbol

10.19322/j.cnki.issn.1006-4710.2016.04.009

2016-01-08

国家自然科学基金资助项目(11571275);陕西省工业科技攻关资助项目(2015GY021)；陕西省教育厅基金资助项目(2015CX009)

沈晓芹，女，博士，副教授，研究方向为微分方程数值解及其应用。E-mail: xqshen@xaut.edu.cn

O186.1

A

1006-4710(2016)04-0428-04