在探索知识中做好顺应、引导和渗透——以“探索两个三角形的三边成比例，它们是否相似”为例

秦旭东（陕西省南郑县教研室）

在探索知识中做好顺应、引导和渗透
——以“探索两个三角形的三边成比例，它们是否相似”为例

秦旭东（陕西省南郑县教研室）

学生在自主探索数学问题中，常会出现与教学预案不同的想法或解答设想，却与理性的解答有一定的距离.较好的处理方法应是，顺应学生的想法，恰当地引导，结合所学知识体系来有机渗透，最终得出理性的解答.这样做有利于调动学生自主探索知识的积极性，也才可展示出教师具有创造性运用教材与驾驭课堂的能力.

顺应想法；恰当引导；有机渗透；知识构建

在自主探索数学问题的过程中，当遇到由个别或部分学生发现的知识、某一作（方）法，不是本节教学内容的重点，且也未列入教师课堂教学的预案之中时，若从宏观角度来分析这个知识或作（方）法，却有利于学生更深层次去认识、去理解、去发现知识，或可为后继学习做伏笔，那么就应顺从学生的想法、作法，并恰当引导，为后继学习渗透下知识、方法等方面的内容，或给学生留下探索、思考与问题解决的内容，来调动学生自主探索知识的积极性．现以“探索两个三角形的三边成比例，两三角形是否相似”为例来说明.

一、课堂实录片断

三角形相似这部分内容在北师大版《义务教育教科书·数学》中是这样编排的：先分别探索出三角形相似的三个判定定理，再整体给出这三个判定定理的证明．为方便阐述本文观点，现回顾笔者在教学该节课的一段课堂实录.

师：同学们前面已经知道了相似三角形的含义，并用画图、测量等作法探索出了两角分别相等的两个三角形相似，两边成比例且夹角相等的两个三角形相似．今天请同学们用类似的方法来探索：如果两个三角形的三边成比例，那么这两个三角形相似吗？

改变k值的大小，再试一试．

师：①在做一做中，给定k的值，可根据前面探索三角形相似的作法来确定，比如可取k=2，3，4，等等；

②这里设法去比较∠A与∠A′的大小有没有什么原因？能否去比较∠B与∠B′，∠C与∠C′的大小呢？同学们先思考，并给出回答与说理．

生1：若根据两边成比例且夹角相等的两个三角形就相似，所以只要能说明∠A=∠A′即可．

教师肯定并强调了生1的回答．

师：生1，生2回答得很好，道理也说得很清楚明了．若要验证△ABC与△A′B′C′相似，请同学们想一想，还需将上述三种情况都一一去验证吗？

生3：老师，没有必要，验证了∠A=∠A′与验证∠B=∠B′或∠C=∠C′的道理是相同的．

师：好的，请同学们选择适当的k值，去画图验证，并能简要说明你是如何来画图的．

教师巡视、指导后，学生画图验证并汇报.

生4：我取的k值是2，作法是先任意画一个△A′B′C′，再分别以△A′B′C′的各边长的2倍来画△ABC，如图1所示，通过测量，发现∠A与∠A′的大小基本相等．

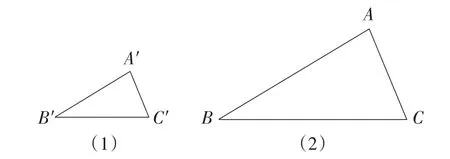
图1

师：有与生4的作法相同的吗？

有几位学生纷纷举手.

师：有与生4作法不同的吗？

生5：老师，我是将△A′B′C′与△ABC画在透明的纸上，采用重合的方法来发现∠A与∠A′的大小也是基本相等．

生6：我是先画△ABC，再分别以为边长来画△A′B′C′，用度量的方法来测量∠A与∠A′大小，也发现∠A与∠A′的大小基本相等．

师：对于k=2时，不管是先任意画△ABC，再去画△A′B′C′，还是先画△A′B′C′，再画△ABC，只要我们作图准确，都可以验证∠A=∠A′.所以当k=2时，△ABC与△A′B′C′相似．从减少求线段长的角度来分析，特别是用尺规来作图时，生4的方法比较简洁，即先画小的图，再画大的图．当k=3，4，…时，其作法与k=2时的方法是类似的，这里就不一一去验证了；当时，同学们想一想其作法与k=2时的画法有何联系与区别呢？先画哪一个三角形比较好？

生7：首先任意画一个△ABC，再去画△A′B′C′，这样比较简单．

师：生7的想法很对，下面请同学去画图验证．……

生8：老师，当k=2时，我的画法与前面的画法不一样，不知对不对？

师：你来展示与说明一下．

生8：我是这样画的，先任意画一个△ABC，再取AB，AC的中点，分别记为点B′，C′，如图2所示，由三角形的中位线性质可知所以△AB′C′就是△A′B′C′，显然∠A=∠A′．

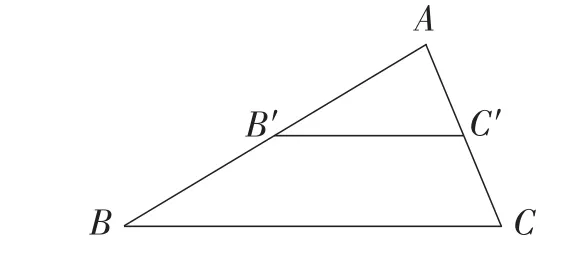
图2

生8在展示与说明的过程中，师生均能专心听，认真地分析．展示完后，教师还引导学生分析了一下，看的出大家都给予了赞赏的目光．接着本节课就转入了此定理的应用与举例的教学之中．

类似生8的作图方法，在一个班上（50人左右）共有10人左右，其中一半仅有作图，无理性思考．从教师方面看，也未曾在备课中给予预设，加之上课追求进度，也未曾深入去研究与从宏观上去认识生8的作法．

二、分析与思考

在这节课的教学中，教师善于引导学生参与数学活动，在问题解决时，能注意引导学生优先思考，找到问题的症结，并让学生动手、动口的相互协调，为大部分学生在解答问题时降低了盲目性，还渗透给学生怎样去抓住并处理问题的关键起到了示范性；学生在画图中，教师能注意选取有代表性的解法（生4的作法），以及普遍性的作法（生6的作法），这对培养学生的优选意识，起到了潜移默化的作用；当学生回答出每一种作法后，教师还能根据教学目标，采用恰当的问题串来引领学生，从而训练了学生用归纳、类比等理性方法来不断获取知识，并把课堂逐步推向高潮，起到了教师是学生建构知识的引领者、促进者的作用．

对生8的作法，也有这样三个问题值得思考.

（1）生8的作法与生4或生6的作法有何联系与区别？

（2）生8中所画的△AB′C′与另画的△A′B′C′有什么关系？

（3）生8的作法虽然只有极少数学生与之相同，那么它有什么积极作用？有没有推广与研究的价值呢？

当生8回答完问题后，教师还应追问△AB′C′与另画的△A′B′C′能否重合或全等？有没有其他情况存在？这是存在性、纯粹性或唯一性的基本要求．要回答这个问题实际上比较简单，由三角形全等知识可知：当三角形三条边长确定后，则所画的三角形是全等的，即生4、生6、生8所画的△ABC若相同，如图3所示，从图形运动变化角度来看，△A′B′C′是△AB′C′平移与旋转等的结果，或者说是将△A′B′C′经过平移与旋转等变化至△ABC上，让点A′与点A重合，A′B′落在AB上，A′C′落在AC上便是．从如何去证明三角形相似的判定定理看，这正是发现证明思路的基本想法与作法．基于此，当学生有类似于生8的方法时，教师应顺从学生的想（作）法，并给予恰当的引导，化消极为积极，这样做不仅是培养学生问题意识，也是培养学生的创新意识，同时，引导学生悟出证明任意两个三角形当满足三边成比例时，两个三角形相似的方法，还应给学生提出当k为任意实数时，该如何将一个三角形转化在另一个三角形上的问题来作为课余探索题，这样可为学生留下思考问题的内容与留下充足的探索问题的时间与空间，从而调动学生去自主研究、自主探索与寻求解决问题的方法与作法，这才可真正体现出教师是在创造性地运用教材与有驾驭教材的能力．

2016—09—12

秦旭东（1966—），男，中学高级教师，主要从事教材教法研究.