工程陶瓷回转表面线电极磨削加工粗糙度预测模型

范久臣， 孙雪梅， 王 帅， 吴东东,3， 阚英男

(1.北华大学 机械工程学院， 吉林 吉林 132021；2.北华大学 数学与统计学院， 吉林 吉林 132013；3.青岛科技大学 自动化学院， 山东 青岛 266042;4.吉林建筑大学 土木工程学院， 吉林 长春 130025)

工程陶瓷回转表面线电极磨削加工粗糙度预测模型

范久臣1， 孙雪梅1， 王 帅2， 吴东东1,3， 阚英男4*

(1.北华大学 机械工程学院， 吉林 吉林 132021；2.北华大学 数学与统计学院， 吉林 吉林 132013；3.青岛科技大学 自动化学院， 山东 青岛 266042;4.吉林建筑大学 土木工程学院， 吉林 长春 130025)

结合电火花线切割机床改进了具有跟踪电极的工程陶瓷回转表面放电磨削装置，利用该装置加工后的表面粗糙度受到3个主要因素的影响：峰值电流、脉冲宽度和脉间比。根据每种因素的不同水平，设计了16组正交试验，利用二次多项式响应面方法建立了3个因素与粗糙度之间的关系模型，即粗糙度预测模型。基于实际试验，将参数估计值和各因素的水平值代入模型，得到粗糙度预测值，进而将其与粗糙度测量值进行了对比。结果表明，所建立的粗糙度预测模型拟合效果良好，有助于工艺参数的选择与加工质量的控制。

表面粗糙度； 正交试验； 二次多项式响应面方法； 粗糙度; 预测

0 引 言

工程陶瓷以其良好的物理性能在各领域获得广泛应用，但自身的高硬度和脆性导致其成为传统机械加工方法难以加工的材料[1]。电火花放电加工方法能对电阻率小于100 Ω·cm的工程陶瓷进行加工[2-3]。利用线切割机床实现工程陶瓷回转体表面的放电磨削加工已经成为现实。吉林大学的团队[4-5]研发了能够带动长圆柱体工程陶瓷绕自身轴线回转的装置，并安装于线切割机床上，实现了线电极与工程陶瓷回转表面之间的放电磨削。加工原理和实物如图1所示。

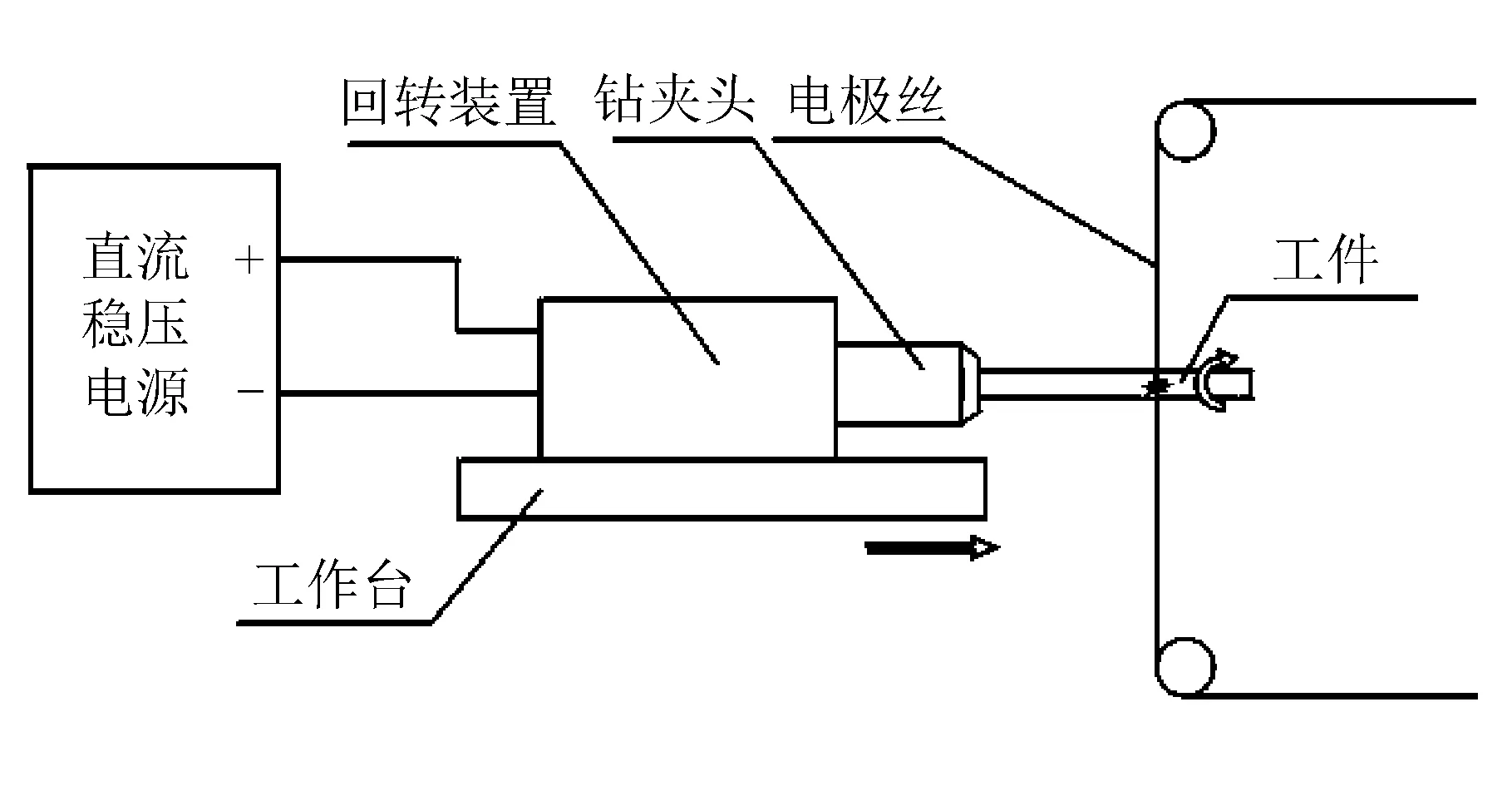
图1 圆柱体工程陶瓷回转装置

图1所示的加工装置在原理上存在不足，即在其他工艺参数相同的情况下，加工回路总电阻随着线电极与陶瓷表面之间放电位置的变化而变化，导致回转表面轴向各点粗糙度不一致。陈利[6-8]等针对这一问题，在装置上添加了跟踪电极，将跟踪电极安装于线切割机床的丝架上，并与回转装置配合，用以夹持陶瓷棒，整套装置模型和实物分别如图2和图3所示。

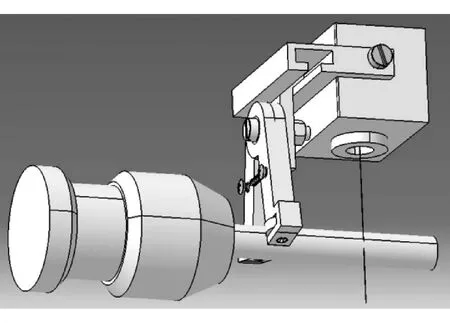
图2 带有跟踪电极的回转装置模型

图3 带有跟踪电极的回转装置实物

图2和图3所示的装置在原理上保证了加工回路总电阻不变，从而回转表面轴向各点粗糙度实现了一致。

1 加工装置的改进及试验

在图2和图3所示的装置上进行了进一步的改进，具体说明如下：

2)将带动回转的直流小功率电机改为较大功率的交流电机，保证了在系统阻力较大的情况下的恒定转速，有利于提高加工质量。

改进后的回转装置及跟踪电极实物如图4所示。

工程陶瓷回转表面放电加工的粗糙度受到众多电加工参数的影响，其中最主要的影响因素为峰值电流、脉冲宽度和脉间比[6]，这3个因素分别用x1，x2，x3表示，加工后的表面粗糙度用y表示。

图4 改进后的带有跟踪电极的回转装置

3个因素的工艺水平(取值)由线切割机床预先设定。3个因素各自对粗糙度有影响，也不排除某两个因素的综合作用对粗糙度产生影响。为了找到多因素综合作用对粗糙度的影响规律，文中采用二次多项式响应面方法[9-11]，建立以x1，x2，x3为自变量，以粗糙度y为因变量的函数，工程陶瓷回转表面放电磨削加工粗糙度的预测模型:

(1)

式中xj----第j个影响因素。xj的参数为βj；x4=x1x2,x5=x1x3,x6=x2x3,x7=x1x1,x8=x2x2,x9=x3x3；则自变量向量为x= (x1,x2,…,xj,x9)，j=1,2,…,m；m=9。

为估计模型参数{βj}，文中根据正交试验表进行了三因素四水平的放电磨削试验，共计16组，每组用i表示；第i组试验的粗糙度测量值表示为yi；第i组试验的第j个影响因素的取值表示为xi,j，i=1,2,…,n；n=16。每组试验结果及工艺参数见表1。

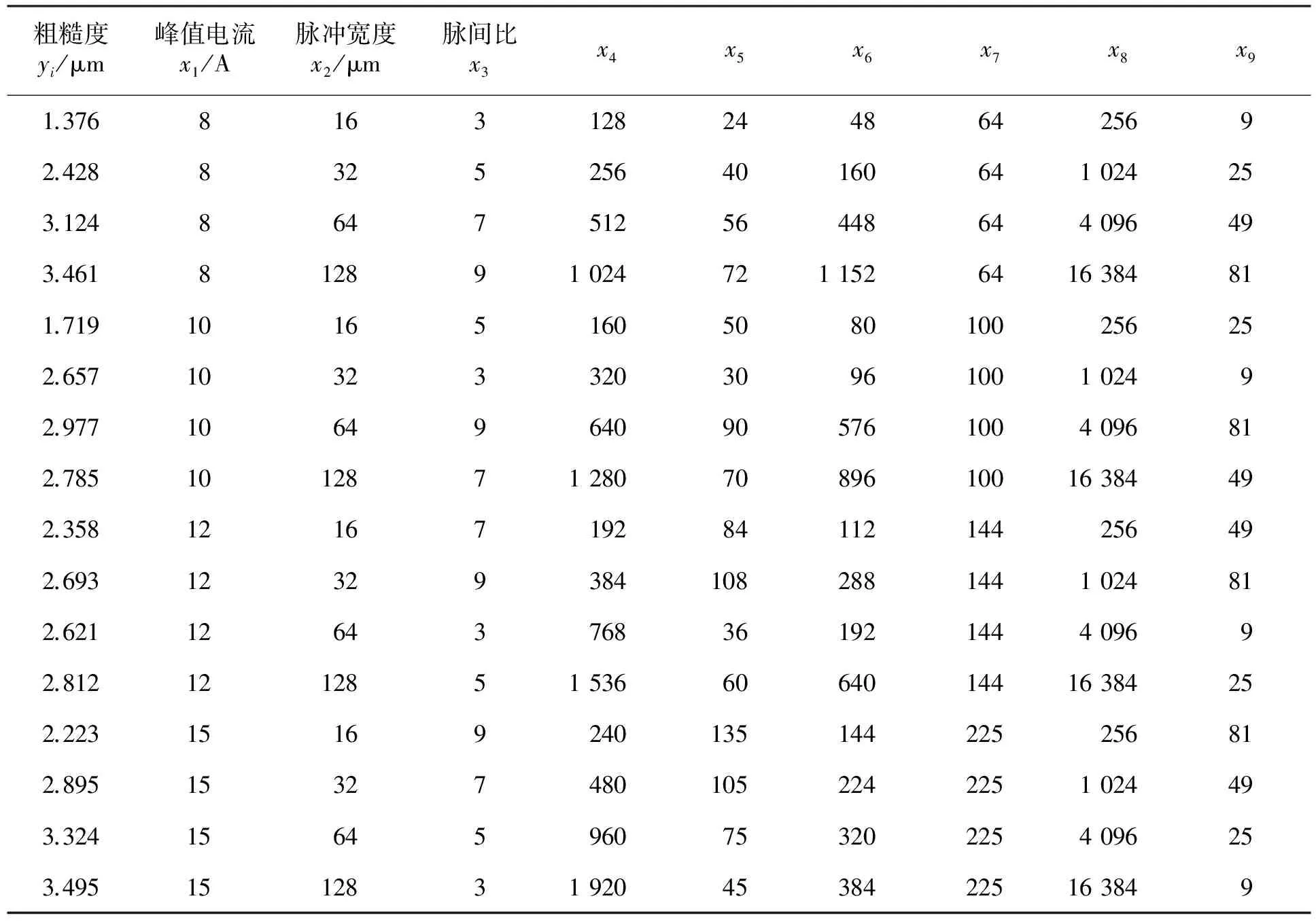
表1 正交试验组及其因素水平

2 建立粗糙度预测模型

根据式(1)的粗糙度预测模型，给定第i组试验各因素的水平(x1,x2,…,xj,x9)，该组试验的粗糙度预测值表示如下：

四是查处违法违规违纪行为。在项目采购人自查自纠中，对 “零报告”和“隐瞒、迟报、谎报”的，列为重点核查对象，一经查实，将对采购人及当事人进行严肃追责。对于查处结果，发现存在一般性违规违纪问题的，督促项目采购主管部门和项目采购人整改到位；存在严重违法违规问题的，将按照法律法规和相关文件要求进行处理，并对当事人进行严肃追责。同时，曝光一批群众反映强烈、情节恶劣的违法违规违纪行为。对涉嫌违纪、职务违法、职务犯罪的，移送纪委监委处理；涉嫌其他犯罪的，依法移交公安等司法机关查处。

(2)

由于有多组数据，因此将所有试验组的输入与输出统一用矩阵表示：

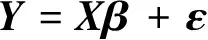
(3)

其中:

而X表示如下:

(4)

经过推导，得到参数的最小二乘估计值为[9]：

(5)

利用Matlab计算得到β的估计值，并根据x4=x1x2,x5=x1x3,x6=x2x3,x7=x1x1,x8=x2x2,x9=x3x3,整理得到最终的预测模型：

y= (-312 703.562 5-39 665.958 7x1+

40 080.547 1x2+562 815.752 4x3-

979.703 1x1x2-46 298.449 7x1x3-

(6)

3 粗糙度模型的验证

在相同的一组工艺水平下，分别利用模型计算出粗糙度的预测值，并用粗糙度测量仪测出粗糙度测量值，进而计算预测值的预测误差。工艺参数、预测值、测量值和预测误差结果见表2。

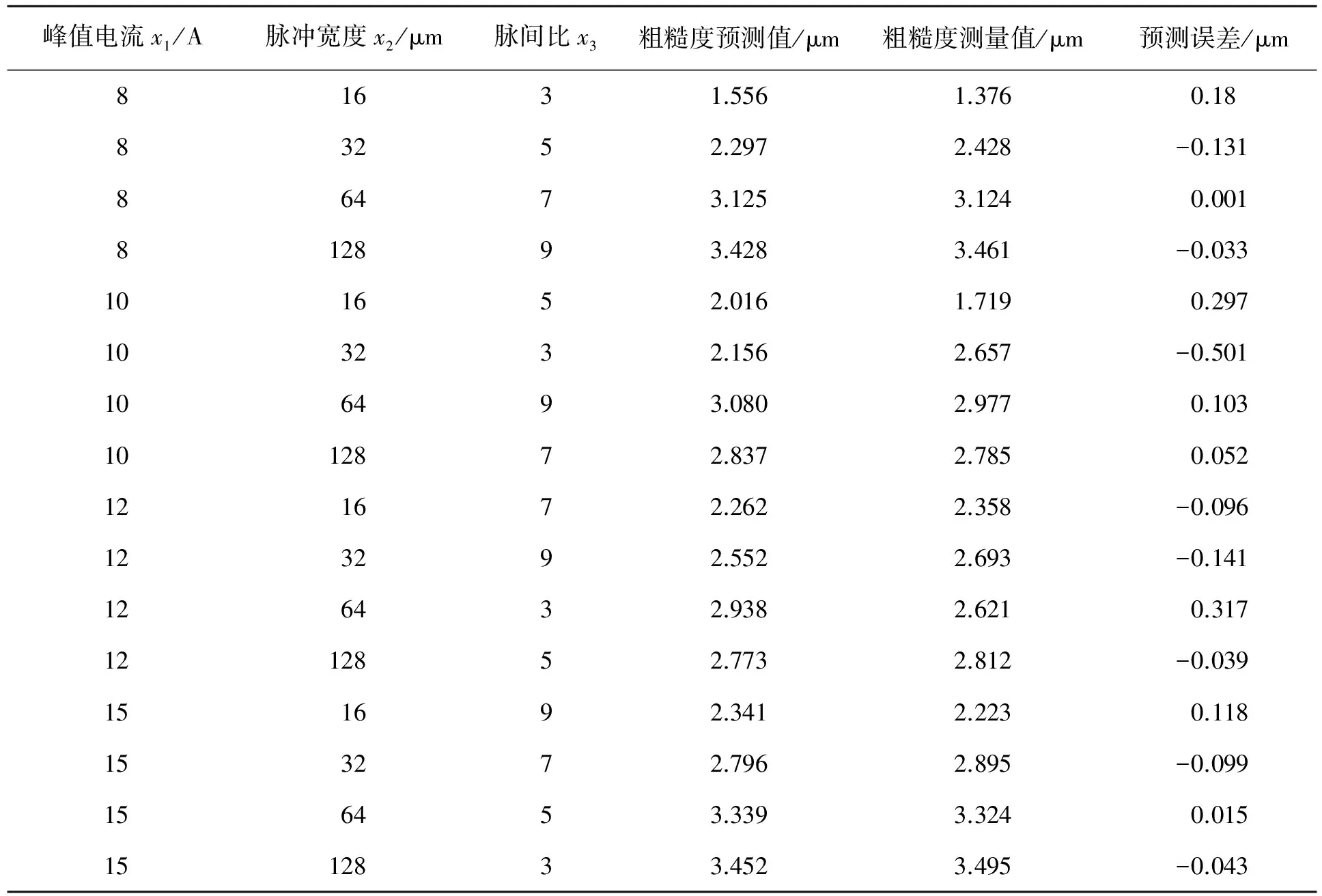
表2 各组试验的粗糙度预测值及测量值对比

根据表2数据，以每组试验为横坐标绘制预测值与测量值的对比曲线，如图5所示。

由表2和图5可知，粗糙度预测模型即式(6)预测的绝对误差最大值为0.317 μm，此时的预测相对误差达到了12%，满足该项研究对预测模型的初期目标20%。

随着工艺参数1～16组的变化，预测值的变化趋势与测量值的变化趋势高度相近。预测值是通过将工艺参数代入式(6)计算得到的。而式(6)中的所有自变量的系数，是由以前的工艺参数及相应的粗糙度测量值通过式(1)～式(5)计算确定的。因此，粗糙度预测模型受工艺参数的影响，且用于确定式(6)的具有不同工艺参数的试验越多，粗糙度预测模型就越逼近真实规律。

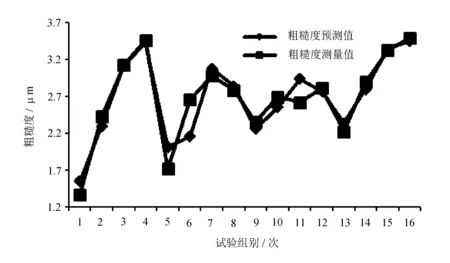
图5 粗糙度预测值与测量值的对比

研究的进一步目标是实现预测模型的相对误差低于10%，而实现这一目标需要：

1)对设备结构进行深入改进,以提高设备精度；

2)增加试验次数，给出更多工艺参数组合并测量相应粗糙度测量值。从而根据式(1)～式(5)，预测模型式(6)的所有自变量的系数会随着试验次数增加不断改进，最终实现预测模型在绝对误差、相对误差和变化趋势方面逼近真实规律。

4 结 语

改进了工程陶瓷回转体表面电火花磨削装置,并进行了正交加工试验。根据试验结果建立了表面粗糙度的预测模型。将预测值与测量值进行对比证明，文中提出的粗糙度预测模型是有效的，可用于表面粗糙度的预测与控制，有助于深入进行工程陶瓷回转表面放电磨削工艺的研究。

[1] 卢晨光,范久臣,孙丽霞.电火花线切割加工技术在陶瓷加工中的应用[J].吉林化工学院学报,2009,26(3)：63-65.

[2] 王望龙,王龙,田欣利,等.工程陶瓷特种加工技术的研究现状与进展[J].机床与液压,2015,43(7)：176-180.

[3] 刘志东,高长水.电火花加工工艺及应用[M].北京:国防工业出版社,2011.

[4] 曹毅.基于线切割机床的碳化硼工程陶瓷回转表面放电加工技术研究[D].长春:吉林大学,2006.

[5] 杨兆军,张立新,王丽慧.工程陶瓷复杂回转表面的线切割加工方法及表面粗糙度研究[J].北京工业大学学报,2008,34(8)：800-805.

[6] 陈利.基于跟踪电极的电火花加工碳化硼陶瓷回转表面的研究[D].长春:吉林大学,2007.

[7] 马宁.具有跟踪电极的放电磨削氧化铝：碳化钛陶瓷回转表面的研究[D].长春:吉林大学,2008.

[8] 张立新.工程陶瓷回转表面的线切割加工技术[D].长春:吉林大学,2009.

[9]KhuriAI,MukhopadhyayS.Responsesurfacemethodology[J].WileyInterdisciplinaryReviewsComputationalStatistics,2010,2(2)：128-149.

[10] 穆雪峰.多学科设计优化代理模型技术的研究和应用[D].南京:南京航空航天大学,2004.

[11] 季晓枫,林凤,邱芳萍.响应面法优化水酶法提取林蛙卵蛋白[J].长春工业大学学报:自然科学版,2013,34(2):137-144.

Roughness prediction model for engineering ceramics rotating surface wire electrical discharge grinding

FAN Jiuchen1, SUN Xuemei1, WANG Shuai2,WU Dongdong1,3, KAN Yingnan4*

(1.College of Mechanical Engineering, Beihua University, Jilin 132021, China;2.College of Mathematics and Statistics, Beihua University, Jilin 132013, China;3.College of Automation, Qingdao University of Science and Technology, Qingdao 266042, China;4.Civil Engineering College of Jilin Jianzhu University, Changchun 130025, China)

For wire electrical discharge machine (WEDM), we update the rotating-surface-grinding device for engineering ceramics grinding. The grinded surface roughness of the ceramics is influenced mainly by the following parameters: peak-current, pulse width and inter-pulse ratio. Based on the parameters, 16 orthogonal experiments are designed and a roughness model presenting the relationship between the parameters and roughness is built with two-degree Response Surface Methodology (RSM). In experiments, both the estimated and real parameters are input to the model to calculate the roughness. The results show than the model is with good fitting performance.

surface roughness； orthogonal experiment； two degree RSM； roughness; prediction.

2016-08-12

吉林省教育厅“十二五”科学技术研究项目(2013438)

范久臣(1973-)，男，汉族，吉林吉林人，北华大学教授，博士，主要从事机械设计制造新技术及其装备研发工作,E-mail:fanjiuchen1973@163.com. *通讯作者：阚英男(1985-)，男，汉族，吉林长春人，吉林建筑大学讲师，博士，主要从事可靠性理论及技术方向研究,E-mail:kanyingnan@163.com.

10.15923/j.cnki.cn22-1382/t.2016.6.04

TH 16

A

1674-1374(2016)06-0535-05