改进的通信信号多径时延估计算法
2017-01-18翟晓光武传华
翟晓光,武传华
(电子工程学院,合肥 230037)
改进的通信信号多径时延估计算法
翟晓光,武传华
(电子工程学院,合肥 230037)
为提高多径条件下通信信号时差定位系统中时延估计的精度,提出了一种利用信号循环平稳特性改进的WRELAX多径时延估计算法,给出了算法推导过程及流程图。新算法结合了循环时延估计算法和多径时延估计算法的优点,既可分辨多径时延,又能很好地抑制噪声及强干扰。仿真结果表明,新算法在多径分辨率及估计精度方面均优于原算法。
时差定位;时延估计;循环平稳;多径
0 引 言
时差定位法(TDOA)是利用无线电信号到达多个不同地点的接收站之间的时间延迟(时差)来进行定位的方法,具有隐蔽性强、对天线要求低、测量精度高等特点,是对无线通信移动台(MS)进行定位的重要手段之一,近年来愈发引起人们的重视。时延估计(TDE)是时差定位中的关键步骤,时延估计精度往往决定了时差定位精度,因此有必要研究精度高、适应性强的时延估计算法。
在实际测量中,由于高山、建筑等障碍物对电磁波的反射和散射,通信信号往往经不同路径传播后到达接收机,各径分量在接收机内相互叠加形成干扰,从而导致了信号在多径环境下进行时延估计的精度降低。此外,时延估计的精度还受到噪声和干扰的影响,强干扰和噪声会影响相关峰的位置,降低时延估计的精度。由时延估计的克拉美罗下限也可得知,信噪比越低,时延估计能达到的精度下限越低。
针对多径信号的时延估计问题,已经有了许多不同算法[1]。最大似然估计法[2](ML)性能达到了所有时延估计方法的上限,但其缺点是运算量大,且无法保证收敛;非线性最小二乘法[3](NLS)应用于多径时延估计时,需要别的方法先给出时延初值,且在时延间隔很小时无法给出估计值;WRELAX方法[4]把一个多维优化问题简化为多个一维优化问题,使运算量大为减小,且WRELAX算法对信号形式没有要求,适合与其他算法相结合。
通信信号大多具有循环平稳性,利用信号循环平稳性进行时延估计能够有效抑制噪声和干扰的影响,提高时延估计精度,文献[5]中提出了几种循环时延估计算法。本文利用循环时延估计算法中的循环相关函数相关法(CCCC)对WRELAX算法进行改进,新算法结合了两者的优点,既能适应低信噪比及强干扰环境,又能分辨多径时延。
1 WRELAX时延估计算法
1.1 多径信号时延估计模型
假设以2个接收机进行时延估计,其中一个接收机接收到的信号由多径叠加而成,则多径信号时延估计模型可以表示为:
x(t)=s(t)+e1(t)+w1(t)
(1)
(2)
式中:x(t)和y(t)为2个接收机接收到的信号;s(t)为感兴趣信号(SOI);w1(t)、w2(t)为干扰信号,一般与SOI有不同的循环频率;e1(t)和e2(t)为高斯噪声,干扰信号与噪声统称为不感兴趣的信号(SNOI);L、al、τl分别对应多径信号数目、第l条多径的衰落幅度以及第l条多径的时延,并假定衰落幅度为实数。
通常假定SOI与SNOI统计独立,但SNOI之间可以是统计相关的。
对式(1)和式(2)进行间隔为Ts的等间隔采样,得到离散后的接收信号:
x(n)=s(n)+e1(n)+w1(n)
(3)
(4)
式中:n=n′Ts,n′=0,1,2,…,N-1。
1.2 WRELAX多径时延估计算法[6]
可将时延估计问题表示为一个对于多径信号幅度和时延差估计的非线性最小二乘问题:
(5)
式中:‖‖表示欧几里得范数。
式(5)是一个多维非线性优化方程,直接求解的计算量极大。WRELAX算法将转化降低为多个一维优化问题,使计算复杂度大大降低。
首先假设在所有L条多径中,只有第l条是未知的,其余L-1条均为已知,则可令第l条多径信号为:
(6)
将式(6)代入式(5)可以得到代价函数为:
(7)
(8)
(9)
综上所述,可以总结出WRELAX算法的步骤:
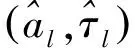
(4) 仿照以上步骤,依此令l=4,5,6,…,不断迭代刷新,直到l等于某预定的多径数目L。

2 循环时延估计算法
由于经过编码、调制、采样等处理过程,使得通信信号呈现出周期平稳的特点,即其统计量会随时间呈周期性的变化,这种信号被称为循环平稳信号[7]。循环平稳过程理论体系中,引入了一种新的变量——循环频率α。循环频率通常与信号的载频、调制方式、码元速率等相关,通过选择不同的循环频率,可以区分不同的信号,并抑制噪声和干扰[8]。
根据参考文献[9]给出的循环相关函数的表达式,式(3)、式(4)中x(n)在循环频率α处的循环自相关函数以及x(n)、y(n)在循环频率α处的循环互相关函数为:
(10)
(11)
式(3)、式(4)中的变量,通常假设噪声e(t)不具有循环平稳特性,干扰信号w(t)与感兴趣信号s(t)具有不同的循环频率,因此可以得到:
(12)

(13)
由式(12)、(13)可以看出,通过引入循环频率,理论上可以完全抑制掉噪声和干扰信号。

(14)
3 改进的WRELAX算法
在常用的多径时延估计算法中,WRELAX算法运算效率较高,且对信号形式没有过多的限制,非常适于与其他算法相结合。CCCC算法有较好的抑制噪声的能力,并且本质上也是利用相关得到时延差值,在此考虑利用CCCC算法对WRELAX算法进行改进,使其在对多径信号有较高分辨力的同时在低信噪比条件下也有较高估计精度。
仍然假设只有第l条多径参数未知,其余L-1条均为已知,可令:
(15)
仿照式(7)写出改进的循环WRELAX算法的代价函数:
(16)
将式(16)中的代价函数展开得:
(17)
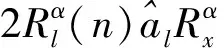
(18)


(19)
(20)
4 仿真分析
为验证算法性能,设计了如下的仿真实验。
实验1:验证算法的多径分辨力。实验中源信号采用二进制相移键控(BPSK)信号,载频10.7MHz,码元速率为fk=1×104Baud,则带宽为20kHz。取循环频率为码元速率,即α=fk。信号采样频率为fs=2MHz,则采样间隔Ts=0.5ms。噪声为加性高斯噪声,信噪比15dB。假设多径数L=2。

图1 改进的WRELAX算法流程图
一般来说,传统相关法的多径分辨力(可分辨的两径信号最小相对时差)约等于信号带宽的倒数,则在本实验中最小可分辨时延差为50 ms。实验中设置两信号时延差分别为45 ms、35 ms、25 ms、15 ms,以检验算法对多径信号的分辨力。10次独立实验后取均值,结果如表1所示。
由表1可以看出,本文提出的改进算法继承了WRELAX算法的优点,在多径时延差为25 ms时仍能准确估计出时延,分辨率比传统的相关算法提高了2倍。同时可以看出,随着2个多径信号时延差值的减小,迭代次数不断增加,也即运算量不断增加。最后,当时延差过小时,算法的估计精度出现显著降低。
实验2:验证算法在不同信噪比条件下的估计性能。源信号参数与实验1相同,多径数L=2,2个径时延差为35 ms,循环频率仍选择α=fk。干扰信号为带宽、载频均与源信号相同的调幅(AM)信号,信干比固定为5 dB。噪声为加性高斯噪声,信噪比由0 dB变化至20 dB,每个信噪比条件下独立实验100 次,计算均方误差。仿真结果如图2所示。

表1 算法对多径信号的分辨力

图2 AM干扰及不同信噪比条件下算法性能对比
由仿真结果可以看出,2种算法的估计精度均随着信噪比的升高而不断提高,本文提出的改进算法估计精度优于原WRELAX算法,且在低信噪比条件下这种优势更加显著。主要原因在于虽然干扰信号与源信号有相同的载频及带宽,但循环频率不同,当取循环频率α=fk时,AM及高斯噪声均不具有循环平稳特性,这使得改进算法能够有效抑制干扰与噪声,估计精度高于原WRELAX算法,这与之前的理论分析是一致的。
5 结束语
本文利用循环时延估计算法对WRELAX多径时延估计算法进行了改进。新算法结合了2种算法的优点,既能分辨多径信号,又能适应强干扰及低信噪比环境。仿真表明,新算法分辨率在15dB时达 到了传统相关时延估计算法的2倍,且在不同信噪比条件下估计精度均优于原WRELAX算法。
[1] 陈韶华,相敬林,罗建.水声信道多径时延估计的高分辨方法研究[J].系统仿真学,2005,17(11):252-255.
[2] STOICA P,SHARMAN K C.Novel eigenanalysis method for direction estimation[C]//Radar and Signal Processing,IEE Proceedings F.IET,1990:19- 26.
[3] VACCARO R J,RAMALINGAM C S,TUFTS D W,et al.Least-squares time-delay estimation for transient signals in a multipath environment[J].The Journal of The Acoustical Society of America,1992,92(1):210- 218.
[4] LI J,WU R.An efficient algorithm for time delay estimation [J].IEEE Transactions on Signal Processing,1998,46(8):2231-2235.
[5] GARDNER W A,CHEN C K.Signal-selective time-difference-of-arrival estimation for passive location of man-made signal sources in highly corruptive environments,Part 1:theory and method[J].IEEE Transactions on signal Prosscessing,1992,40(5):1168-1184.
[6] 刘姗.无线传感器网络节点定位中关键技术研究[D].天津:天津大学,2014.
[7] GARDE W A.Measurement of spectral correlation[J].IEEE Transactions on ASSP,1986,34(5):1111- 1123.
[8] 刘洋,邱天爽,毕峰.循环时延估计方法相互关系研究[J].大连理工大学学报,2012,52(4):589-593.
[9] FONG G,GARDNER W A,SCHELL S V.An algorithm for improved signal-selective time-difference estimation for cyclostationary signals[J].Signal Processing Letters,IEEE,1994,1(2):38-40.
[10]GARDNER W A,CHEN C K.Signal-selective time-difference-of-arrival estimation for passive location of man-made signal sources in highly corruptive environments,Part 2:algorthms and performance[J].IEEE Transactions on signal Prosscessing,1992,40(5):1185- 1197.
Improved Time Delay Estimation Algorithm for Communication Signals in Multi-path Environment
ZHAI Xiao-guang,WU Chuan-hua
(Electronic Engineering Institute,Hefei 230037,China)
To improve the time delay estimation precision of communication signals in time difference of arrival location system under the multi-path condition,this paper puts forwards an improved WRELAX multi-path time delay estimation algorithm by using signal cycle stationary performance,presents the derivation process and flow chart of the algorithm.The new algorithm combines the advantages of both cyclic time delay estimation algorithm and multi-path time delay estimation algorithm,which not only can distinguish the multi-path time delay,but also can suppress the noises and strong jamming.Simulation results show that the new algorithm performs better than the original algorithm on both multi-path resolution and estimation precision.
time difference of arrival location;time delay estimation;cycle stationary;multi-path
2016-05-12
TN911.23
A
CN32-1413(2016)06-0104-04
10.16426/j.cnki.jcdzdk.2016.06.022
