压制干扰对雷达探测区域影响的二维可视化方法

商 乐，戴家君

(解放军91404部队，秦皇岛 066001)

压制干扰对雷达探测区域影响的二维可视化方法

商 乐，戴家君

(解放军91404部队，秦皇岛 066001)

研究了压制干扰的仿真数学模型和Matlab仿真结果，将模型应用于雷达对抗仿真系统中，实现压制干扰对雷达探测区域影响的二维可视化，动态表现雷达对抗态势。该系统已应用于工程项目中，取得了较好的效果。

压制干扰；雷达探测区域；雷达对抗；仿真模型

0 引 言

压制干扰下雷达探测区域是压制干扰研究中常用的干扰度量指标。以往对探测区域的仿真大多是一种静态的仿真结果，即预先设定雷达、干扰设备和目标性能参数以及其载体平台位置参数，进行一次仿真，得到一次评估结果。这种研究方法适合研究人员对对抗装备、对抗手段的研究，但不能满足在瞬息万变的实战中指挥员对战场态势变化充分了解的需求。因此，本文立足于该需求，研究压制干扰的各种数学模型和计算方法，在雷达对抗仿真系统中充分考虑仿真中雷达、目标和干扰机参数在仿真系统运行过程中的实时变化，实现压制干扰对雷达探测区域影响的二维可视化。

1 压制干扰效能评估指标

评估压制干扰效能的指标有探测距离、雷达暴露区、压制系数、自卫距离、检测概率-距离曲线等等。

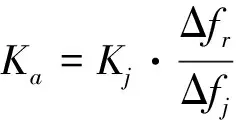
干扰压制的空间体积称为压制区，在压制区内，雷达无法发现目标回波信号，即雷达接收机输入端的干扰-信号功率比大于等于压制系数。如果仅研究干扰所压制的平面面积，如方位×距离、仰角×距离，则这个平面为干扰扇面。如果仅研究一维空间上的干扰效果，则用最小干扰距离表示。

压制系数是研究干扰效能最重要的参数，在雷达对抗仿真系统中，压制干扰下雷达探测区域的显示是干扰效能最为直观的表现方法。

2 压制干扰计算方法

2.1 关键技术

2.1.1 平台空间关系

在雷达对抗仿真系统中，动态仿真必须研究仿真过程中实时变化的参数对仿真显示的影响，如雷达天线扫描方式、雷达天线方向图、干扰天线主瓣方向等参数。雷达天线、目标和干扰机天线三者的瞬时角度关系如图1所示。

图1 雷达天线、目标和干扰机天线角度关系

当干扰机天线主瓣方向对准雷达，且雷达主瓣方向对准干扰机时，干扰信号能量能够最大程度地进入雷达接收机，从而产生最大的干扰效能。从图中可以看出，雷达天线主瓣方向和干扰机天线主瓣方向都偏离了雷达与干扰机的连线，进入雷达接收机的干扰信号能量相对较少，干扰效能较差。

另一方面，各平台运动方式和实时位置等对雷达、目标和干扰机的距离产生影响，某时刻三者的距离关系如图2所示。

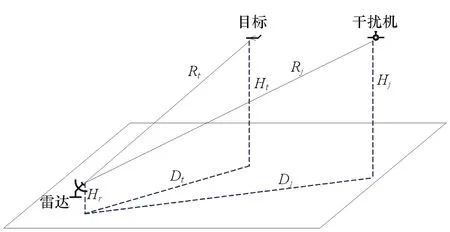
图2 雷达、目标和干扰机距离关系

计算的结果在二维态势显示系统中表现的距离是水平面内的距离，因此有下列距离换算公式：

(1)

(2)

2.1.2 坐标转换模型

仿真过程中，各机动平台位置不断变化，要求实时解算各平台间距离关系。由于平台位置是以经纬度的形式给出，因此要考虑地球曲率半径对距离计算的影响。为将经纬度的信息及时地转换为地理坐标信息，从计算速度、实时性和适应性等多方面综合考虑决定采用Boring算法[2]，因为其不但可以达到足够的精度，且公式结构简单、运算速度快、适应性强，受计算机精度影响最小。实现方法如下：

(3)

(4)

(5)

(6)

(7)

则：

(8)

E=sinDcosW

(9)

(10)

(11)

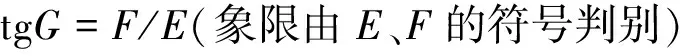
(12)

(13)

(14)

(15)

式中：e=0.006 738 524 1；λM为原点的经度；φM为原点的纬度；λT为目标点的经度；φT为目标点的纬度；RMT为原点到目标点的距离；AMT为原点到目标点的方位。

采用Boring算法就可以快速求解基于经纬度的地球表面任意两点的直线距离方位关系。

2.1.3 天线方向图模型

雷达天线向外辐射和接收电磁能时，在三维空间中的分布可以表示成相对(归一化)基础上的曲线，称为辐射方向图[3]。方向图通常用天线功率增益因子G(θ)/G(雷达天线副瓣/主瓣增益比)来描述。压制干扰研究中，天线方向图描述了雷达天线各个方向上辐射能量的分布状况，反映了干扰信号从各个方向进入雷达接收机能量差别，是非常重要的压制区计算参数。常见的天线方向图模型有高斯天线方向图、余割平方天线方向图等。雷达对抗仿真系统中采用高斯天线方向图模型[4]。其主瓣方向图为：

(16)

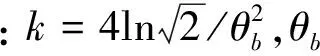
主瓣以外的方向图为：

(17)

式中：k=1.391 6/sin(0.5θb)。

若用功率方向图时，还需要将其平方。θb=15°时仿真结果如图3、图4所示。

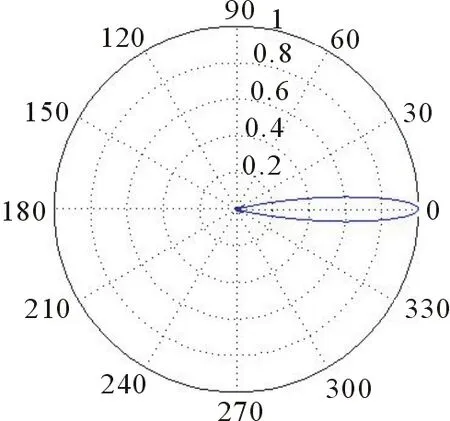
图3 高斯天线波束形状图

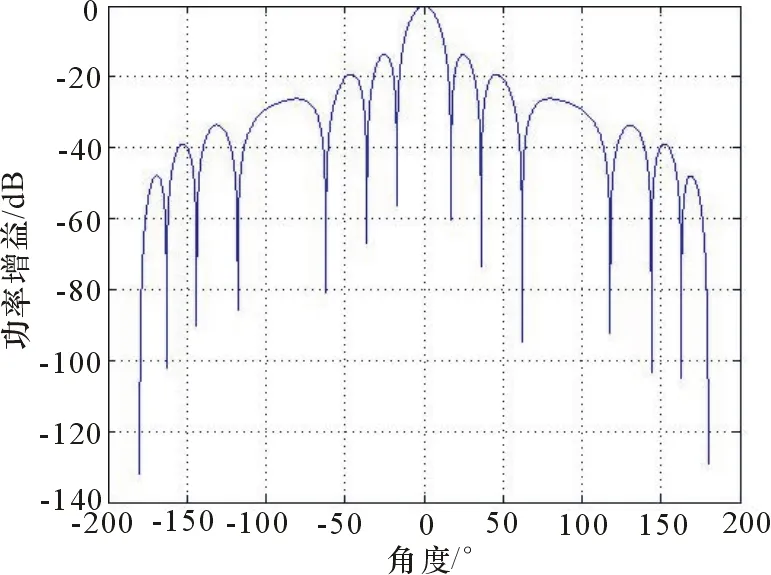
图4 归一化高斯天线方向图

从图3和图4可以看出，高斯天线方向图的特点是具有较多的副瓣，且主副瓣比大，能量比较集中(图3中因天线副瓣相对主瓣能量很小而不明显)。

2.2 信号仿真模型

2.2.1 目标信号功率

目标信号功率为：

(18)

式中：Prs为接收机输入端的目标回波信号；Pt为雷达发射机输出功率；Gt为雷达发射天线增益；Gr为雷达接收天线增益；F为雷达发射信号中心频率；Rt为雷达与目标距离；σ为目标雷达截面积；c为光度。

(1) 当Rt为雷达最大探测距离时，Prs就代表雷达能够检测到的最小回波信号即接收机灵敏度Smin；

(2) 当采用脉冲压缩雷达时，设脉压比为D，则综合信噪比改善因子可近似为0.8D倍；

(3) 当采用脉冲积累来判别目标回波信号时，则目标信号功率乘以积累改善因子M；

(4) 当采用收发公用天线时，有Gt=Gr；

(5) 当目标偏离雷达天线轴时，即θt≠0，有Gt=Gr=Gt(θt)。

综合以上几点，可以得到目标信号功率为：

(19)

式中：Lr为雷达的综合损耗。

2.2.2 干扰信号功率

干扰信号功率为：

(20)

式中：Prj为雷达接收机接收到的干扰信号；γj为干扰信号对雷达天线的极化损失(圆极化取0.5)；Rj为干扰机与雷达的距离；F为雷达工作频率；Gj(φ)为干扰机天线在雷达方向上的增益，并有：

(21)

式中：Gj为干扰机天线主瓣方向增益；φ0.5为干扰机波瓣宽度；φ为侦察机对雷达定位的误差角(通常假设取0)；K为常数，取0.04～0.10，对于高增益锐方向天线，K=0.07～0.10,对于波束较宽、增益较低的天线，K=0.04～0.06。

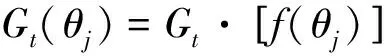
(22)

J/S≥Kj

(23)

(24)

式中：PjGj(φ)为有效干扰功率；PtGt(θt)为有效雷达功率。

2.2.3 噪声信号功率

接收机噪声主要由接收机中的馈线、放电保护器、高频放大器或混频器等产生，它服从零均值正态分布，方差σn2=kTB,k为波尔斯曼常数(1.38×10-23J/K)，T为绝对温度(常温取290K)，B为接收机带宽(Hz)。因此，最大噪声功率(额定噪声功率)Pn=kTB[5]。

接收机灵敏度与噪声信号功率密切相关，接收机灵敏度(Smin)是指接收机正常工作时可以接收到的最小信号电平，由接收机内部热噪声Pn、接收机噪声系数Fn和检测所需的最小信噪比(SNR)min决定：

(25)

2.3 干扰仿真模型

2.3.1 自卫干扰模型

当干扰机主瓣方向对准雷达，干扰机偏离雷达主瓣方向θj=θt，从而有Gj(φ)=Gj，Rt=Rj，Gt(θj)=Gt(θt),由公式(24)化简得：

(26)

雷达和干扰机参数一定，雷达天线对准干扰机的情况下，θt=0，式(26)右端为一常数，记为R0，即烧穿距离或雷达自卫距离。仿真条件：

(1) 雷达参数：功率103W，频率7×109Hz，主瓣增益45，旁瓣增益6，等效噪声温度290K，接收机带宽106Hz，综合损耗10dB，虚警概率10-7，极限灵敏度-96dB。

(2) 自卫干扰机参数：功率2×103Hz，增益10，带宽200×106Hz，RCS为9m2，与雷达的距离250×103m，相对雷达的方位180°。

仿真结果如图5所示。

图5 自卫干扰仿真

图中心的“+”表示雷达，“*”表示自卫干扰机，大圆表示雷达未受干扰时的探测范围，心形圆表示雷达受到自卫式干扰时的压制边界，中心小圆表示雷达的烧穿距离圈。从图中可以看出，雷达的探测范围在压制干扰下，探测范围大幅减小，雷达无法有效地发现目标。

2.3.2 单干扰机支援干扰模型

当干扰机天线主瓣方向对准雷达时，干扰机偏离雷达主瓣方向θj，目标偏离雷达主瓣方向θt，有Gj(φ)=Gj，则：

(27)

考虑雷达、目标和干扰机的空间距离关系，如图2所示。利用式(27)得：

(28)

仿真条件：

(1) 雷达参数和自卫干扰仿真条件相同；

(2) 干扰机参数：功率2×103W，增益10，带宽200×106Hz，与雷达的距离250×103m，相对雷达的方位150°；

(3) 目标参数：RCS为9 m2，与雷达的距离150×103m，相对雷达的方位180°。

仿真结果如图6所示。

图6 单部干扰机支援干扰仿真

图中“◇”符号表示目标，其它符号和线的含义与前一仿真结果相同。从图中可以看出，雷达的探测范围在压制干扰下，探测范围大幅减小，特别在干扰机方向上，探测距离最短。雷达无法发现目标。

2.3.3 多干扰支援干扰模型

多干扰机同时对1部雷达实施干扰，且天线主瓣方向对准雷达，仿真条件：

(1) 干扰机1位置参数：与雷达的距离400×103m，相对雷达的方位150°；

(2) 干扰机2位置参数：与雷达的距离400×103m，相对雷达的方位180°；

(3) 干扰机3位置参数：与雷达的距离400×103m，相对雷达的方位210°。

其它参数与前一仿真相同，仿真结果如图7所示。

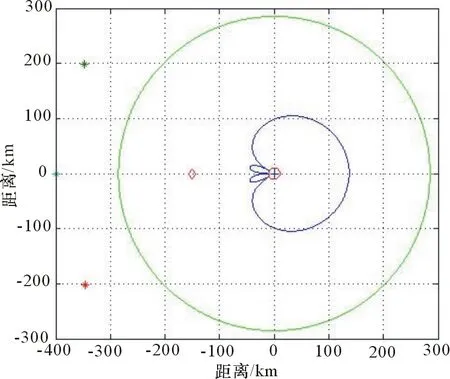
图7 3部干扰机对雷达实施压制干扰

图中符号和线的含义与前一仿真结果相同。从图中可以看出，雷达的探测范围在3部干扰机同时实施的压制干扰下，在干扰机方向上的探测距离减小明显，其它方向距离也大幅减小，雷达无法发现目标。

3 雷达对抗仿真系统中应用实例

在上述压制干扰研究的基础上开发的雷达对抗仿真系统的二维可视化界面如图8所示。

图8 压制干扰条件下雷达探测区域二维可视化

该实例中的对抗兵力模型包括干扰机1、干扰机2、舰艇1和舰艇2，两舰艇上各搭载1部搜索雷达。仿真中假设干扰机的频率范围已覆盖舰载雷达的频率，且干扰方向为全向360°，因此在对抗算法解算中干扰信号能量取干扰机功率和增益的乘积值，即全向等效辐射功率。对抗兵力模型参数如表1、表2所示。

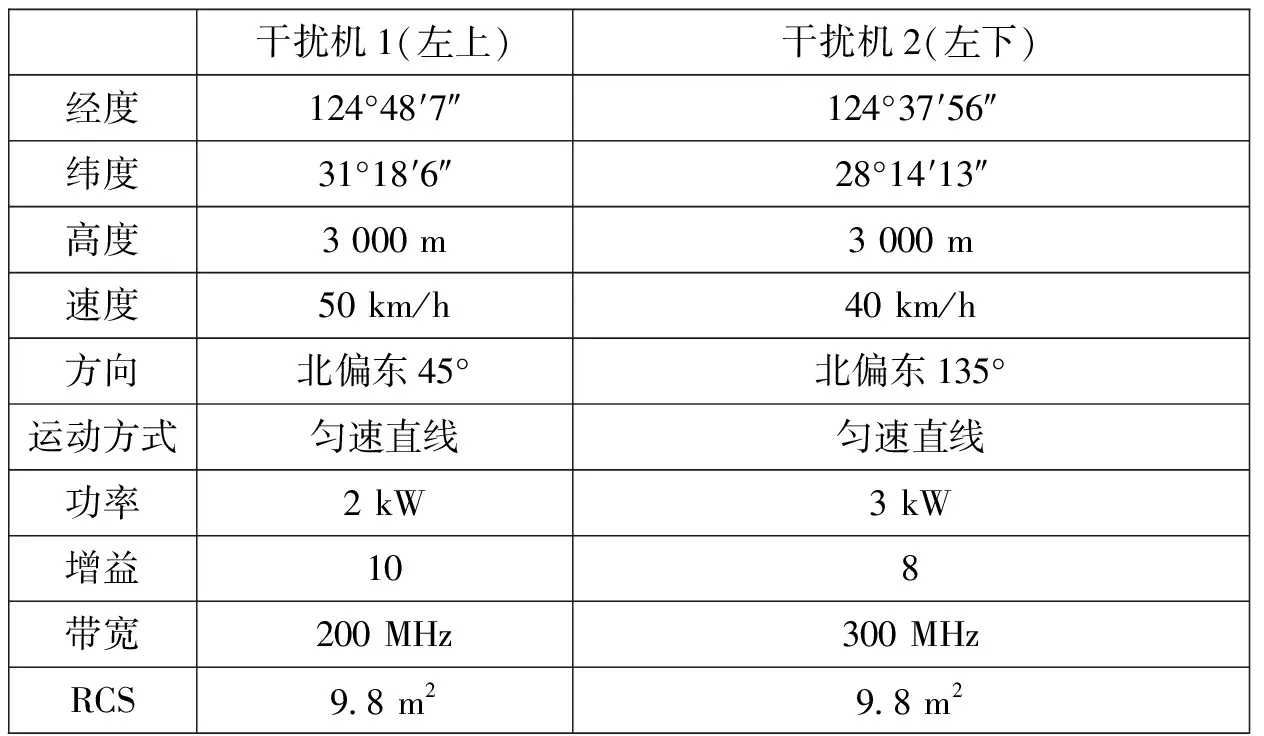
表1 干扰机模型参数表

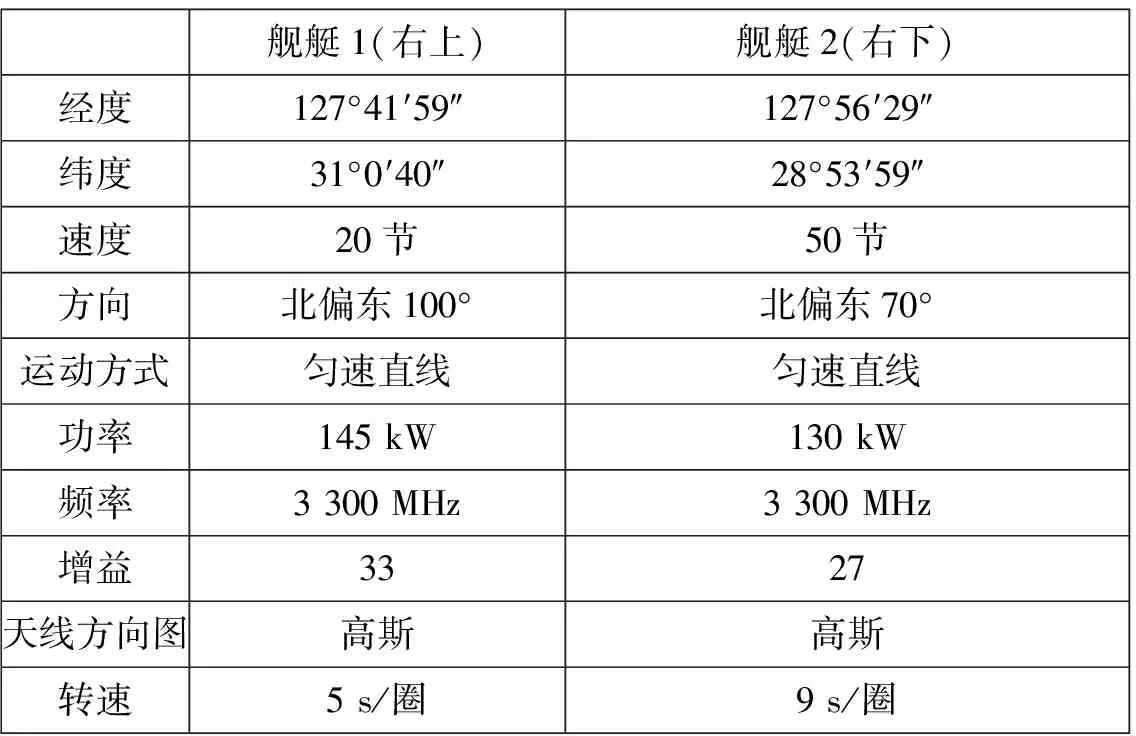
表2 舰艇及其雷达模型参数表

图8中2条闭合虚线分别表示舰载雷达的探测区域边界。当雷达目标处于该边界范围之内时，雷 达发现目标；当雷达目标处于该边界范围之外时，雷达不能发现目标。仿真开始后，各仿真兵力按照各自预设路径轨迹运动，雷达发射波束的天线方向图分别以雷达所在坐标点为中心，按天线转速进行旋转，方向图主瓣的顶点落在雷达探测区域边界上；2架干扰机同时对2艘舰艇上的雷达进行压制干扰，雷达的探测区域出现不同程度的缩小，特别在2架干扰机方向上，舰艇1和舰艇2平台上的雷达探测距离大幅减小。这样干扰机就能够为干扰方提供一定的支援干扰，掩护其它作战兵力接近敌方舰船，遂行作战任务。

4 结束语

在对压制干扰相关数学模型进行研究和仿真的基础上，重点考虑工程应用中需要注意和解决的问题和关键技术，在雷达对抗仿真系统中实现了压制干扰对雷达探测区域影响的二维可视化，具有较好的实用价值。

[1] 邵国培.电子对抗作战效能分析[M].北京:解放军出版社,1998.

[2] 李相民,吴保宁,范洪达.Boring算法定位精度分析[J].火力指挥与控制,1995,21(3):32-35.

[3] SKOLNIK M I.Radar Handbook[M].王军,林强,米慈中,等译.北京:电子工业出版社,2003.

[4] 王国玉,汪连栋.雷达电子战系统数学仿真与评估[M].北京:国防工业出版社,2004.

[5] 丁鹭飞,耿富录.雷达原理[M].西安:西安电子科技大学出版社,2005.

[6] 田秀丽,崔亦斌,王国平.电子干扰条件下地空导弹雷达干扰压制区计算方法[J].现代防御技术,2008,36(4):111-115.

[7] 王国玉,肖顺平,汪连栋.电子系统建模仿真与评估[M].长沙：国防科技大学出版社,1999.

2-D Visual Method of Blanket Jamming Influencing Radar Coverage

SHANG Le，DAI Jia-jun

(Unit 91404 of PLA,Qinhuangdao,066001，China)

This paper studies the simulation maths model and Matlab simulation result of blanket jamming,uses the model into radar countermeasure simulation system,realizes the 2-D visual of blanket jamming to radar coverage,represents the dynamic situation of radar countermeasure.The system has already been applied to engineering items and good effect has been fetched.

blanket jamming;radar coverage;radar countermeasure;simulation model

2016-05-02

TN974

A

CN32-1413(2016)06-0027-05

10.16426/j.cnki.jcdzdk.2016.06.005