一种高精度频率估计的抗噪声调幅干扰算法
2017-01-18闵柏成王思远
闵柏成,张 允,王思远
(中国船舶重工集团公司第723研究所,扬州 225001)
一种高精度频率估计的抗噪声调幅干扰算法
闵柏成,张 允,王思远
(中国船舶重工集团公司第723研究所,扬州 225001)
噪声调幅干扰对消中,干扰频率估计精度较低将导致干扰对消效果严重退化。针对此问题,提出一种基于高精度干扰频率估计的噪声调幅干扰对消方法。该方法首先对Candon算法和Rife算法中谱线的幅值作线性融合处理,然后基于内插离散傅里叶变换,分割离散频谱区域,最后对干扰信号解调并利用频域对消方法抑制干扰。仿真结果表明,该方法具有良好的频率估计性能并能在强干扰背景下有效地抑制噪声调幅干扰。
噪声调幅;频率估计;Rife算法;干扰抑制
0 引 言
噪声调幅干扰[1]是雷达对抗中一种重要的干扰方式,具有信号产生简单、带宽可变、压制效果明显等优点,已成为瞄准式及复合式干扰的重要组成部分。随着干扰技术的发展,进入雷达接收机的干扰信号能量可超过雷达回波信号达数10 dB以上,雷达回波信号完全淹没于干扰信号中。在强干扰背景下,通过估计干扰的特征参数,采用对消方法抑制干扰,提高信号处理增益是现代雷达的一个重要抗干扰手段。因此,有效提取干扰信号的特征参数是实现干扰对消的重要前提。
针对噪声调幅干扰中心频率的估计,目前已有多种有效的分析方法。文献[2]~[3]提出的直接快速傅里叶变换(FFT)方法,对接收信号做FFT,通过搜索最大谱线的位置实现频率估计,但随着DFT量化频率逐渐远离真实频率时,其频率估计精度下降。文献[4]提出了基于离散傅里叶变换(DFT)相位差法的频率估计方法,该方法对接收信号分段后再做FFT,通过分段后频谱峰值处的相位差实现频率估计,但该方法由于噪声调幅干扰中调制噪声的影响存在相位模糊问题,频率估计误差较大。为避免离散傅里叶变换(DFT)产生的频谱泄露问题,文献[5]~[6]提出了Rife算法,根据最大谱线和次大谱线的幅值关系修正DFT量化频率和真实频率的频率偏差,但在量化频率接近真实频率时,该方法估计出的频率偏差值偏大。另外,国外学者如Macleod[7]、Jacobsen[8]、Candan[9]等提出了Candon算法,这些方法均采用DFT的峰值谱线及其左右相邻谱线处幅值的非线性关系,进而估计DFT量化频率与真实频率的频率偏差,但应用到噪声调幅干扰中调制噪声对谱线的幅值影响较大,很大程度降低了该类方法的频率估计精度。
为克服噪声调幅干扰中调制噪声对Candon算法及Rife算法的影响,提高干扰中心频率的估计精度,本文对Candon算法和Rife算法中谱线的幅值进行线性融合,消除调制噪声的影响。针对Rife算法中DFT量化频率与真实频率接近时频率偏差估计较大的问题,采用内插离散傅里叶变换(IpDFT)法细化分割频谱区域,在不同的分割区域内自适应估计最佳的频率偏差。对干扰信号解调,利用频域对消的方法抑制干扰。仿真结果表明,本文所提的方法能准确地估计噪声调幅干扰的中心频率,具有优良的鲁棒性,并能在强干扰背景下有效地抑制噪声调幅干扰。
1 噪声调幅干扰抑制原理
设雷达接收机接收到的信号为:
x(t)=s(t)+j(t)+n(t)= A(t)ej2πfct[U0+Un(t)]ej(2πfjt+φ)+n(t)
(1)

为了在强干扰条件下实现雷达信号处理,需要尽可能地抑制干扰,增强接收信号信干比。根据式(1)中接收信号的模型,如果能够准确估计噪声调幅干扰的载波参数(载频、初相),并对干扰进行解调,通过分析解调后干扰与回波信号在频域上的特点,可以实现干扰对消,达到抑制干扰的目的[10]。
若能够准确估计噪声调幅干扰信号的中心频率及初相,可对式(1)进行解调,得:
(2)
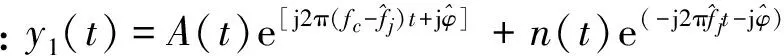
一般情况下,干扰调制频率无法精确对准雷达回波信号频率,即fc≠fj,雷达基带信号A(t)为复包络,从而y1(t)为复信号,而y2(t)为实信号,则利用干扰信号及雷达信号的不同频域结构,对消干扰信号。对y(t)做傅里叶变换,有:
(3)
式中:Y(f)=FT(y(t));Y1(f)=FT(y1(t));Y2(f)=FT(y2(t))。

2 频率估计算法
2.1 直接FFT算法
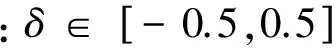
(4)
(5)
2.2 Rife算法和Candon算法
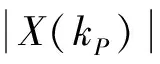
(6)

Candon算法是利用最大谱线以及其相邻谱线幅值的非线性关系估计δ。其中Candon算法频偏修正公式为:
(7)
式中:N为FFT的点数,当N值足够大时,第1个因子项近似为-1,第2个因子项给出了FFT峰值谱线及相邻谱线非线性关系的表达式。
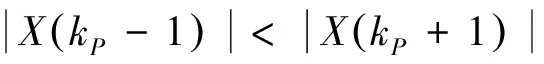
2.3 基于内插离散傅里叶变换的频率估计方法
(8)
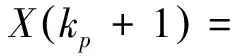
(9)
综上分析,高精度的频率估计算法具体实现如下:
步骤1:对雷达接收信号做N点FFT,搜索频谱的峰值位置kP。
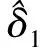
此频率估计算法简单,在不同的分割区域内自适应选择最佳的频率偏差估计,消除了调制噪声对频率估计精度的影响,实现了噪声调幅干扰的高精度频率估计。
3 仿真结果及分析
雷达信号为线性调频(LFM)信号[11],中心频率f0=4 000 Hz,带宽B=1 500 Hz,采样频率fs=8 000 Hz,N=1 024,干扰信号的中心频率fj=4 000 Hz,初相φj=π/6,调制系数取1。
图1(a)和图1(b)分别是线性调频信号和噪声调幅干扰的幅频图。从2幅图可看出噪声调幅干扰的中心频率所对应的谱线恰好对准LFM信号的中频附近实施干扰,且调制噪声的带宽几乎覆盖了LFM信号的带宽。随着信干比的减小,噪声调幅干扰从瞄准式干扰[12]逐渐变为压制式干扰。图1(c)和图1(d)分别是信干比为0 dB和-40 dB时混合信号的幅频图。图1(c)中信干比较大,噪声调幅干扰主要表现为瞄准式干扰,图1(d)中信干比较小,干扰信号的频谱完全覆盖了有用信号的频谱。
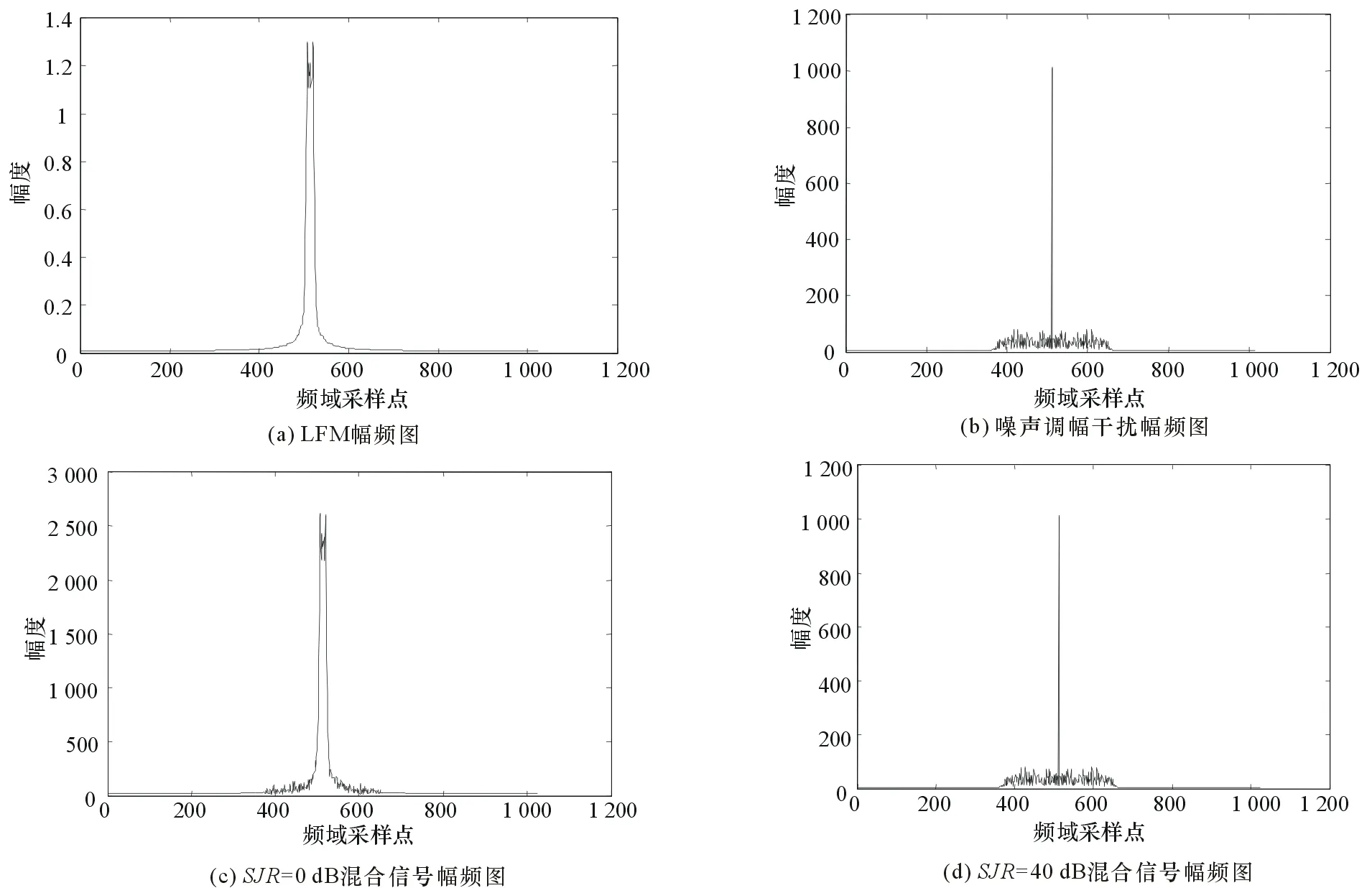
图1 瞄准式干扰和压制式干扰比较
通过图1可以看出,强干扰背景下干扰信号的频谱完全覆盖了有用信号的频谱,当信干比为-40 dB时,压制式干扰效果明显,因此令信干比SJR为-40,其他参数不变,经过100次Monte Carlo实验,得到表1所示各方法的频率估计值。可以看出,改进算法得到的频率估计结果较其他3种方法更准确。
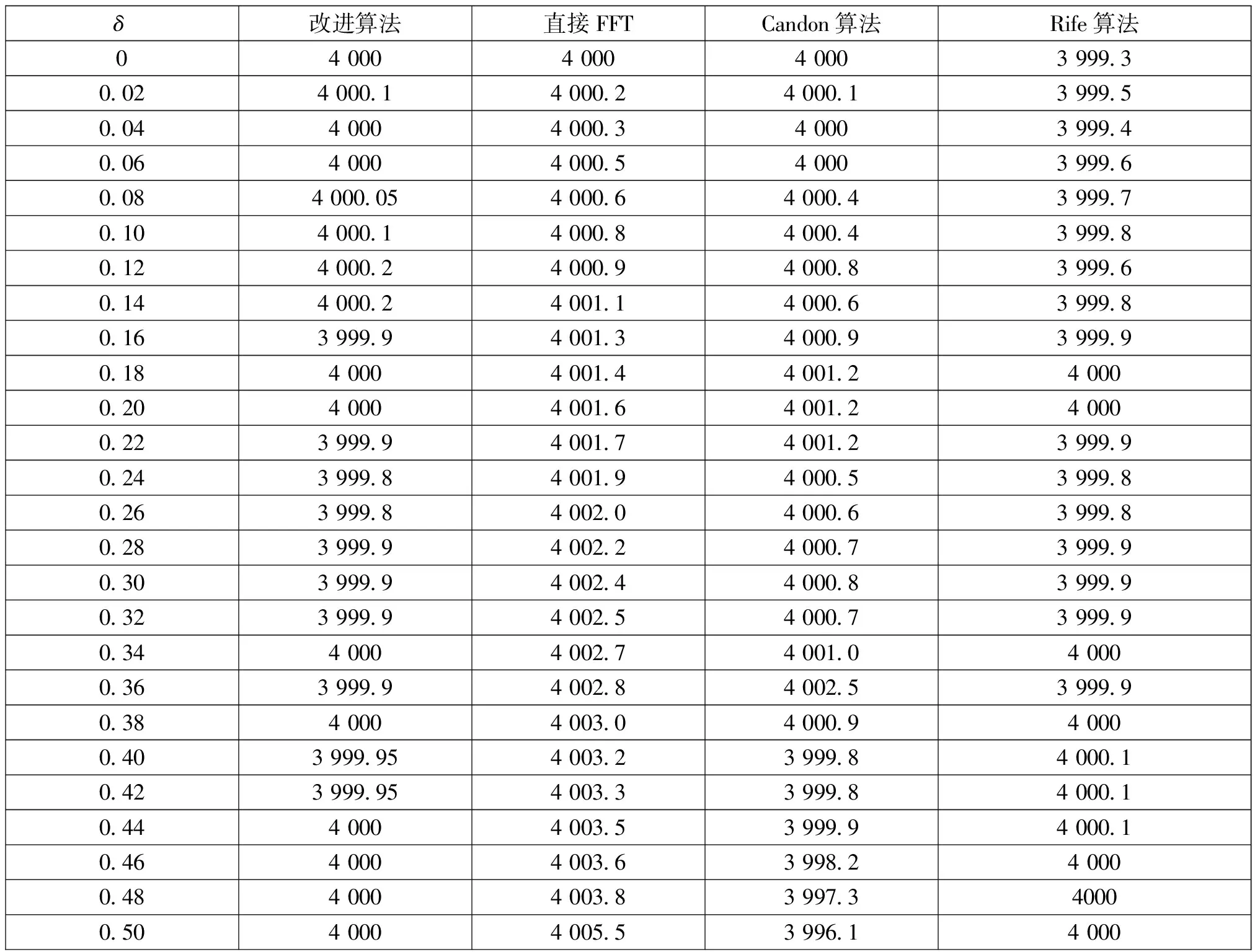
表1 各方法频率估计对比

图2 频率估计精度对比
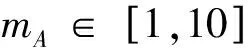

图3 参数A和B随最大调制系数的变化情况
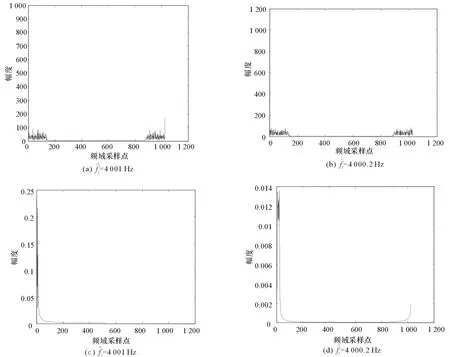
图4 2种干扰频率下干扰的解调及对消效果对比
4 结束语
针对噪声调幅干扰的中心频率估计精度低,干扰对消效果失效的问题,提出一种高精度频率估计的抗噪声调幅干扰算法。对Candon算法和Rife算法中谱线的幅值进行线性融合,可有效抑制调制噪声对干扰频率估计精度的影响。采用IpDFT引入2个参数对DFT谱峰与DTFT谱峰处所覆盖的频谱区域作插值处理,可在不同的分割区域内自适应估计最佳的频率偏差。最后对干扰信号进行解调以及频域对消。仿真结果表明,本文方法较直接FFT算法、Rife算法以及Rife算法具有更高的频率估计精度,克服了噪声调幅干扰中调制噪声对频率估计精度的影响,同时插值处理细化分割了离散频谱区域,使得该方法在不同的分割区域内自适应选择最佳的频率偏差估计。通过对参数A和B随最大调制系数变化的数值仿真,验证了该算法的普适性,进而达到良好的对消效果,并有效地抑制了噪声调幅干扰。
[1] 赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社,2012.
[2] 刘渝.快速高精度正弦波频率估计综合算法[J].电子学报,1999(6):126-128.
[3] 王飞,郑继刚.雷达信号载频精确估计的一种方法[J].舰船电子对抗,2006,29(2):28-64.
[4] 齐国清,贾欣乐.插值FFT估计正弦信号频率的精度分析[J].电子学报,2004(4):625-629.
[5] RIFE D C,BOORSTYN R R.Signal-tone parameter estimation from discrete-time observation[J].IEEE Transactions on Information Theory,1974,20(5):591-598.
[6] 邓振森,刘渝,王志忠,等.正弦波频率估计的修正Rife算法[J].数据采样与处理,2006,21(4):473-477.
[7] MACLEOD M D.Fast nearly ML estimation of the parameters of real or complex single tones or resolved multiple tones[J].IEEE Transactions on Signal Process,1998,46(1):141-148.
[8] JACOBSEN E,KOOTSOOKOS P.Fast,accurate frequency estimators[J].IEEE Siganal Processing Magazine,2007,24(3):125-127.
[9] CANDON C A.A method for fine resolution frequency estimation from three DFT samples[J].IEEE Signal Processing Letters,2011,18(6): 351-354.
[10]杜东平,唐斌.基于频域对消的噪声调幅干扰抑制算法
[J].电子学报,2007,29(3):557-559.
[11]金艳,段鹏婷,姬红兵,等.复杂噪声环境下基于LVD的LFM信号参数估计[J].电子与信息学报, 2014,36(5):1106-1112.
[12]涂友超,赵惠昌,邓建平,等.伪码调相正弦调频复合引信抗瞄准式噪声调幅干扰性能研究[J].探测与控制学报,2007,30(1):29-33.
[13]宋扬,关赛飞,路翠华,刘华章,等.基于自适应引信噪声调幅干扰抑制[J].海军航空工程学院学报,2013,28(6):661-664.
An Algorithm Antagonizing Noise AM Jamming of High Accuracy Frequency Estimation
MIN Bai-cheng,ZHANG Yun,WANG Si-yuan
(The 723 Institute of CSIC,Shanghai 201802,China)
In noise amplitude modulation (AM) jamming elimination,lower accuracy of jamming frequency estimation will result in serious degradation of jamming elimination effect.Aiming at the problem,this paper puts forward a noise AM jamming elimination method based on jamming frequency estimation with high accuracy.The method firstly performs linear fusion processing to the amplitude of spectral line in Candon algorithm and Rife algorithm,then divides the discrete spectrum region based on interpolated discrete Fourier transform,finally demodulates the jamming signal and uses frequency region elimination method to suppress the jamming.The simulation result shows that the method has favorable frequency estimation performance and can effectively restrain noise AM jamming in strong jamming background.
noise amplitude modulation;frequency estimation;Rife algorithm;jamming suppression
2016-06-16
TN974
A
CN32-1413(2016)06-0087-07
10.16426/j.cnki.jcdzdk.2016.06.019
