基于类MUSIC的DOA估计算法

赵德功

(解放军91404部队，秦皇岛 066001)

基于类MUSIC的DOA估计算法

赵德功

(解放军91404部队，秦皇岛 066001)

针对相关信号波达方向(DOA)的估计问题，提出了一种基于最大差值子矩阵的信号DOA估计方法。对利用Toepllitz构造的满秩矩阵进行特征值分解，得到排序后的特征值，并利用特征值的差值实现满秩矩阵筛选，同时结合传统MUSIC 算法实现信号DOA估计。理论分析与仿真实验表明，本文所提方法在相关信号DOA估计方面具有更好的分辨力。

波达方向估计；相关信号；Toeplitz 矩阵

0 引 言

利用传感器进行波达方向估计是信号处理的重要研究方向，在雷达、声纳以及无线通信等领域具有广泛的应用[1-2]。基于噪声子空间的多重信号分类(MUSIC)、求根形式多重信号分类(Root-MUSIC)以及信号频率估计(ESPRIT)[3]等算法可以突破瑞利限，提高DOA估计的精度，但对于信号个数未知的情况，子空间算法的应用具有局限性。基于最小均方误差无失真响应(MVDR)算法[4]尽管不需要信号源个数等先验知识，但瑞利限制会使波达方向(DOA)的估计精度降低。上述传统方法需要相关矩阵非奇异，即假定信号源间不相关。但是，多径传播、敌方转发干扰等应用场景都可能导致信号源之间相关。

针对相关矩阵奇异的问题，目前的主要解决方法有阵列数据空间平滑处理(SS)算法[5-6]以及基于Toeplitz子矩阵算法。空间平滑处理算法通过对接收数据进行平滑，使得相关矩阵满秩，但只适用于方向矩阵具有范德蒙德结构的阵列。Han在其文章中[7]介绍了Toeplitz算法，但该算法主要有2个缺陷：(1)需要信号源个数作为先验知识；(2)利用多个相关子矩阵进行DOA估计并对最终结果进行平均处理，而没有考虑估计结果的性能。Qian在Han基础上进行了改进[8]，使得DOA估计利用多个相关子矩阵，提高了估计的准确度，由于Qian的算法思想类似MVDR，因此DOA估计精度有所下降。

针对上述方法的不足，本文提出基于Toeplitz子矩阵特征值差值筛选的DOA估计方法。该方法首先利用二阶梯度对信号源个数进行估计，利用Toeplitz子矩阵的特征值进行差值筛选，得到最优Toeplitz子矩阵估计，并结合MUSIC算法对信号DOA进行估计。本文主要分为4个部分：(1)对传统的信号模型进行介绍；(2)论述本文思路以及创新点；(3)对不同算法进行仿真分析；(4)全文总结。

1 信号模型

假设P个窄带远场信号源(信号波束方向分别来自θ1、θ2、θ3…θP)以平面波的形式入射到2M+1个阵元组成的均匀直线阵上，且相关信号源个数为K。以第1个阵元接收的信号c1(t)作为参考，则第k个相关信号可以表示为：

ck(t)=ρkejδφkc1(t),k=1,2,…,K

(1)

式中：ρk为信号衰减后的幅度；δφk为第k个信号与参考信号之间的相位差。

对于第m个阵元的接收信号：

(2)

式中：d为相邻阵元的宽度；nm(t)为第m个阵元接收的均值为零、方差为σ2的高斯白噪声。

将直线阵列接收的信号写成矩阵形式:

(3)

(4)

给出x(t)的协方差矩阵:

(5)

利用Han[8]的结论，R第m行n列的元素可表示为：

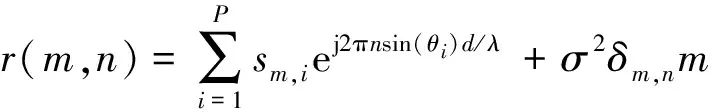
n=-M,…,M

(6)

其中:

sm,i=

(7)

Pi,j具体形式为：

(8)

δm,n为冲激函数:

(9)

选出R中第m列构造Toeplitz矩阵:

Rm=

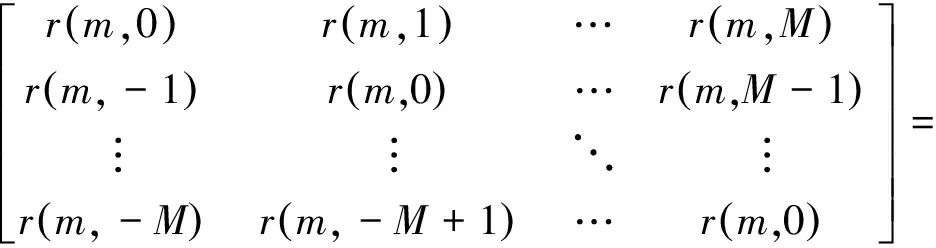
(10)

(11)

由公式(7)可知，Rm为满秩矩阵。在信号源个数已知的情况下，将Rm与MUSIC相结合即可实现信号DOA估计。

2 基于类MUSIC的DOA估计算法

借助矩阵变换容易得到Rm，在Han的文献中，作者尝试将不同Rm得到的结果进行平均，从而提高估计的鲁棒性。在信号源个数未知的情况下将Rm与MUSIC相结合依然存在2个问题：(1)信号源个数的确认；(2)多个Rm如何实现更优的选择。

2.1 信号源个数估计

本文采用二阶差分最大准则估计信号源个数。为了增大特征值之间的差异，同时避免Rm估计不准带来的估计误差，定义:

(12)

F可以理解为Rm二阶矩的均值。对F进行奇异值分解(SVD)：

(13)

当信号子空间仅剩噪声时，特征值曲线二阶差分最大，以此对信号源个数进行估计。当信号源个数小于3时，二阶差分不存在，对特征值进行首位补零操作以解决该问题。得到信号源个数估计：

(14)

2.2 Toeplitz矩阵筛选

信号源个数估计以后，将Rm与MUSIC算法结合即可实现DOA估计。区别于传统的平均值法[1]。对于样本数量有限的情形，Rm为近似估计，因而不可避免引入估计误差。相关矩阵的特征值与对应信号能量成正比例关系，本文引入筛选准则：子空间分解后，信号能量与噪声能量差值越大，则Rm估计越合理。对Rm进行SVD分解：

(15)

定义:

(16)

给出Rm筛选表达式:

(17)

根据MUSIC算法，得到类MUSIC谱估计:

(18)

3 仿真试验

仿真实验主要分为3个部分。首先针对不同阵元数目的场景，对比分析信号源数目估计性能；其次论证基于最大差值筛选相关矩阵的有效性；最后对比分析信号估计的性能。假设存在3个信号源，波达方向分别为(-35°, 10°, 38°)，对于远场窄带信号，假设信号功率近似相等，并假设针对阵元数目为9(M =4)，噪声为加性高斯白噪声，对应信噪比分别设为-10dB、0dB以及10dB。

仿真1：信号源数目估计

为了论证信号源个数估计的有效性，将本文的算法与直接基于Rm(以m =M为例)的二阶差分估计进行对比，每组分别进行100次实验。

表1和表2给出了信号源个数的估计结果，可以看出，对于相关以及非相关信号，基于二阶差分的信号源数目估计算法有效。对比表1和表2，可以看出基于F判定准则的估计方式对于相关信号以及非相关信号均得到最佳估计，基于F的判定准则具有良好的鲁棒性。图1给出了基于Rm准则估计错误的示意图。

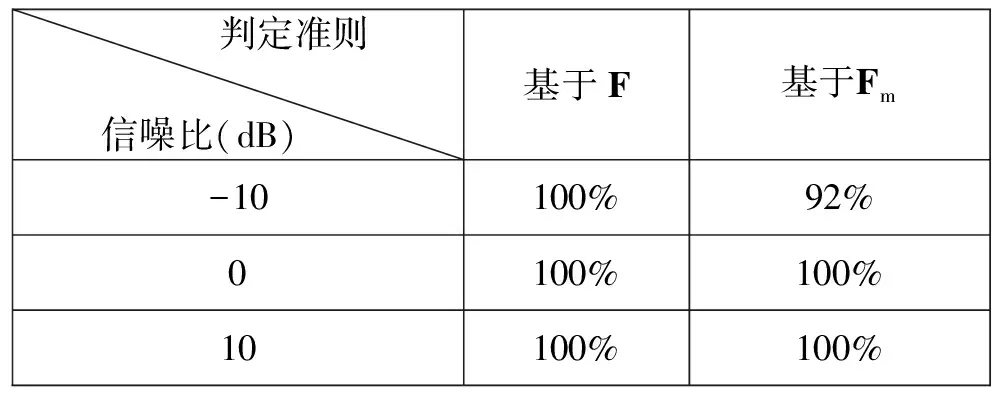
表1 非相关信号源个数估计准确率对比

表2 相关信号源个数估计准确率对比

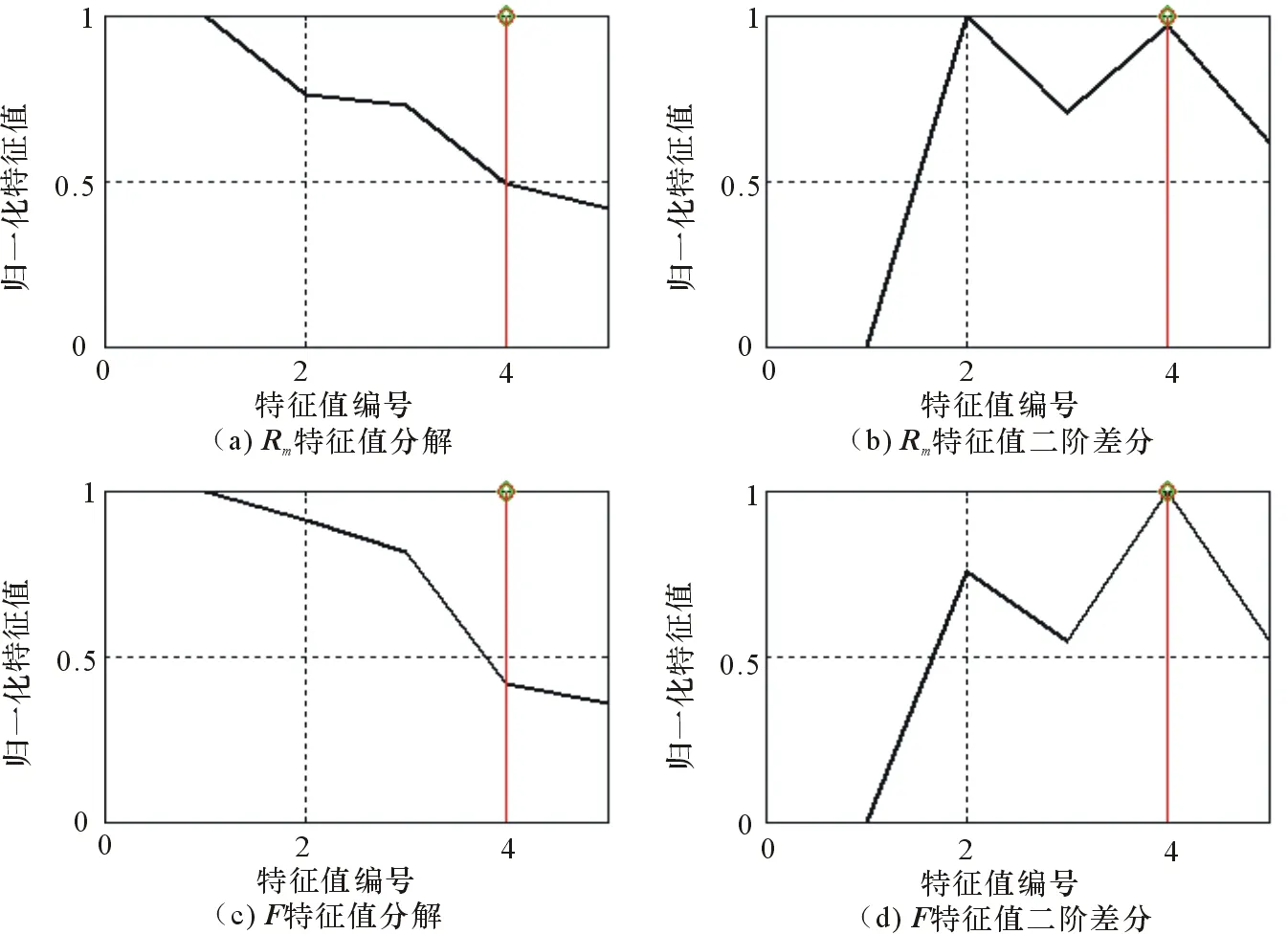
图1 基于F以及Rm判定准则对比示意图

仿真2：基于最大差值的相关矩阵筛选

基于Toeplitz矩阵主要解决相关信号的估计问题，本文仅针对不同信噪比的相关信号进行对比分析。为了对比分析差值筛选的有效性，分别对比差值最大和最小情况下的估计。图2～图4分别给出信噪比为-10dB、0dB以及10dB的估计结果。通过结果图对比，可观察到2个现象：(1)随着信噪比的增加，最大差值与最小差值的差值逐渐增大；(2)每组实验结果都表明，最大差值的估计优于最小差值的估计。该现象证明了本文思路的有效性。

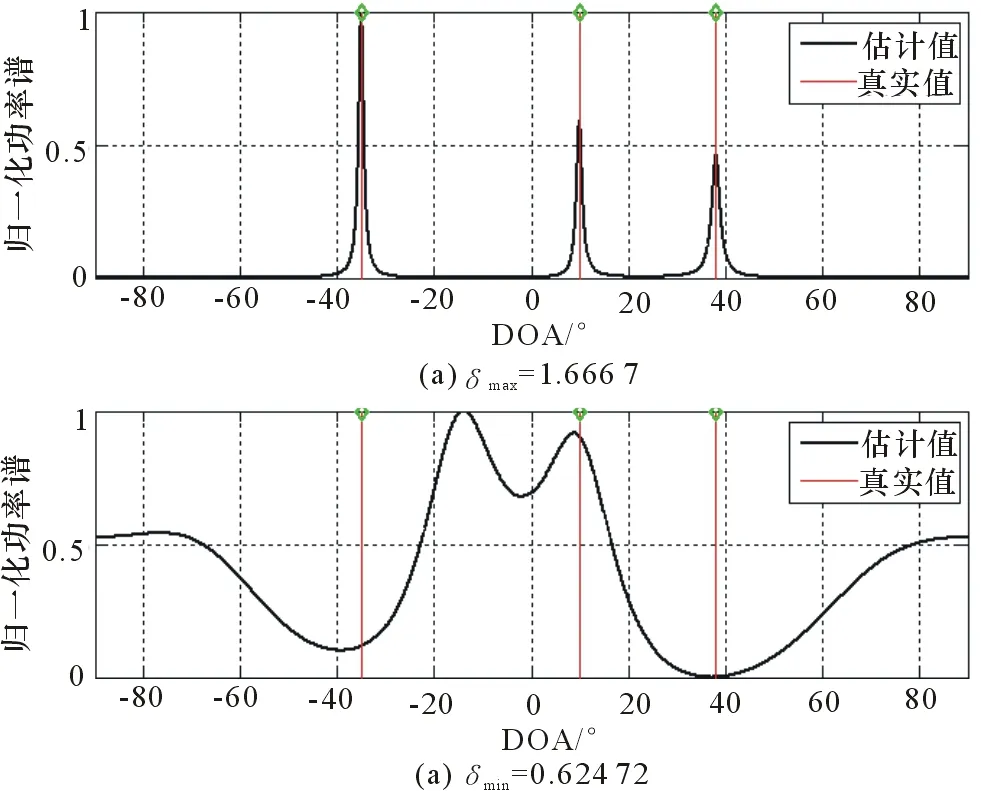
图2 -10 dB的相关信号估计

图3 0 dB的相关信号估计

图4 10 dB的相关信号估计

仿真3：DOA估计性能分析

将本文方法分别与MVDR、MUSIC、MeanToeplitz和ModifyToeplitz4种方法进行对比，随机实验50次，估计误差为随机实验的平均误差。图5和图6分别给出相关信号DOA估计以及非相关信号DOA估计结果。结果表明，对于相关信号DOA估计问题，由于MUSIC依赖于信号的非相关特性构造子空间，因而性能下降最为严重。Toeplitz矩阵以牺牲分辨率为代价，因此对于非相关信号，该类算法性能相比MVDR和MUSIC的估计性能都有所下降。对比图5和图6，可以观察到基于最大差值的类MUSIC算法较基于均值的Toeplitz估计性能更优，实验结果论证了本文算法的有效性。

图5 相关信号DOA估计误差示意图

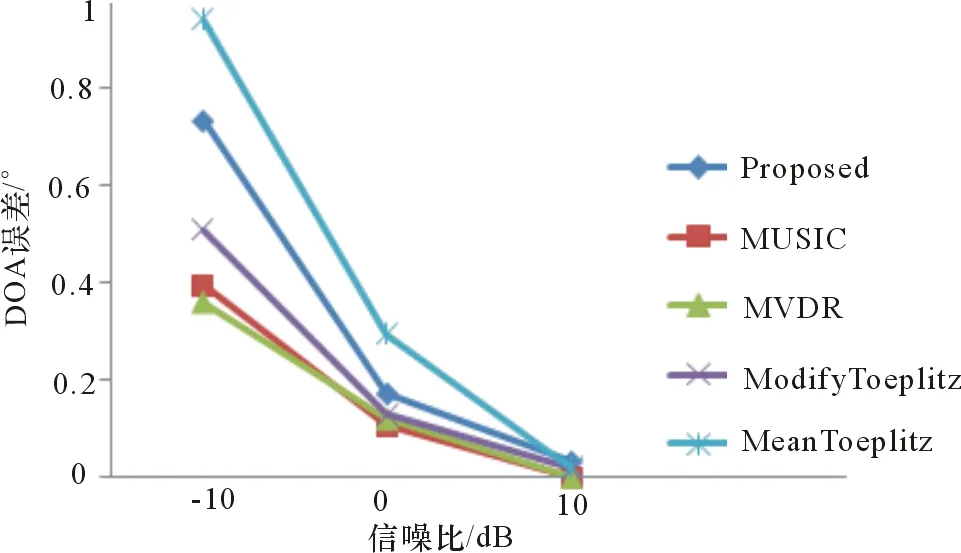
图6 非相关信号DOA估计误差示意图

4 结束语

本文在传统MUSIC算法以及Toeplitz矩阵的基础上，提出了一种新的DOA估计算法。该算法主要有2个创新点：(1)提出利用相关矩阵二阶矩和补零操作相结合的信号源个数估计方法；(2)提出利用最大差值对Toeplitz进行筛选的方法。实验结果证明了本文思路的合理性以及算法的有效性。

[1]BEKKERMANI,TABRIKIANJ.TargetdetectionandlocalizationusingMIMOradarsandsonar[J].IEEETransactionsonSignalProcessing,2006,54(10):3873-3883.

[2]WONGKT,ZOLTOWSKIMD.Closed-formunderwateracousticdirection-findingwitharbitratilyspacedhydrophonesatunknownlocations[J].IEEEJournalofOceanicEngineering,1997,22(3)566-575.

[3]ROYR,KAILATHT.ESPRIT-estimationofsignalparametersviarotationalinvariancetechniques[J].IEEETransactionsonSignalProcessing,1989,37(7):297-301.

[4]CAPONJ.High-resolutionfrequency-wavenumberspectrumanalysis[J].IEEESignalsProcessingLetters,1981,69(11)：1380-1419.

[5]SHANTJ,KAILATHT.Adaptivebeamformingforcoherentsignalsandinterference[J].IEEETransactionsonSignalProcessing,1985,33(3):527-536.

[6]PILLAISU,KWONBH.Forward-backwardspatialsmoothingtechniqueforcoherentsignalidentification[J].IEEETransactionsonSignalProcessing,1989,37(1):8-15.

[7]HANFM,ZHANGXD.AnESPRIT-likealgorithmforcoherentDOAestimation[J].IEEEAntennasandWirelessPropagationLetters,2005,4(1):443-446.

[8]QIANC,HUANGL,XIAOY.LocalizationofcoherentsignalswithoutsourcenumberknowledgeinunkownspatiallycorrelatedGaussiannoise[J].IEEESiganlProcessinglett.,2015,63(20):5355-5368.

DOA Estimation Algorithm Based on MUSIC-like

ZHAO De-gong

(Unit 91404 of PLA，Qinhuangdao 066001，China)

Aiming at the problem of direction of arrival (DOA) estimation of correlation signal,this paper puts forward a signal DOA estimation method based on the maximal difference value sub-array,performs eigenvalue decomposition to the full rank matrix constructed by Toepllitz,fetches the eigenvalue after sequencing,and uses the difference value of eigenvalue to realize full rank matrix filtration,as well as realizes signal DOA estimation combining with traditional MUSIC algorithm.The theory analysis and simulation experiment show that the method proposed in this paper has better resolution in DOA estimation of correlation signal.

direction of arrival estimation;correlation signal;Toeplita matrix

2016-10-09

TN911.7

A

CN32-1413(2016)06-0069-04

10.16426/j.cnki.jcdzdk.2016.06.015