光学拼接焦平面重叠像元数计算

褚 备，李富强，常君磊



光学拼接焦平面重叠像元数计算

褚 备，李富强，常君磊

( 北京空间机电研究所，北京100094 )

针对光学拼接焦平面的图像漏缝问题，本文提出了一种基于误差分析的CCD拼接像元数计算方法。首先，基于相机成像原理建立了焦面光学拼接的模型。结合像方远心和非远心光路系统的特点，对导致漏缝的因素进行分析。对反射镜导致渐晕区的传函下降问题，给出了拼接像元数的计算公式｡最后，将该方法应用于焦平面实例，结果表明，CCD拼接不存在漏缝现象｡

光学拼接；焦平面；重叠像元；图像漏缝

0 引 言

随着遥感技术的发展，遥感相机的幅宽和分辨率不断提高。CCD器件作为遥感相机常用的图像传感器，由于技术和工艺的限制，单片CCD长度不能满足宽视场的要求[1-2]｡因此，采用多片CCD拼接来增大焦平面视场已成为当前遥感相机满足大幅宽需求的主要手段[3]｡目前常用的拼接方式主要有视场拼接和光学拼接[4-5]。光学拼接是利用反射镜将视场分割成若干个空间分离的子视场，再将子视场的图像拼接起来实现无缝拼接方式。光学拼接按照分光元件的不同又可分为半反半透式、折射式和全反全透式。

采用反射镜的全反全透式光学拼接具有能量利用率高、拼接长度较长、无像差、多片CCD可以同时成像、工作时重叠区不受姿态影响等优点，成为具有广泛应用前景的拼接技术，是拼接主要发展方向[6]。

对于全反全透式光学拼接，不可避免都存在渐晕问题，也会对光学传递函数造成影响[7]。在光学拼接过程中，由于焦面分光设计误差，反射镜加工误差及拼接装调误差等因素可能会导致CCD重叠区中心偏离渐晕区中心，从而导致CCD拼接的漏缝问题。

本文针对光学拼接漏缝问题的因素进行分析，并结合渐晕区MTF下降给出了搭接像元数的计算公式。

1 模型建立及影响重叠区漏缝因素分析

1.1 模型建立

对于全反全透式的光学拼接，主要通过拼接反射镜实现，拼接反射镜通常位于光学系统出瞳和焦平面之间，焦平面光学拼接模型如图1和图2所示。在图1中，为光学系统的出瞳直径，为拼接反射镜的长度，充满出瞳的光线经过拼接反射镜的切割，在焦平面(即CCD感光面)上分别形成渐晕区和，CCD重叠区长度为。拼接反射镜对光线的切割如图2所示。

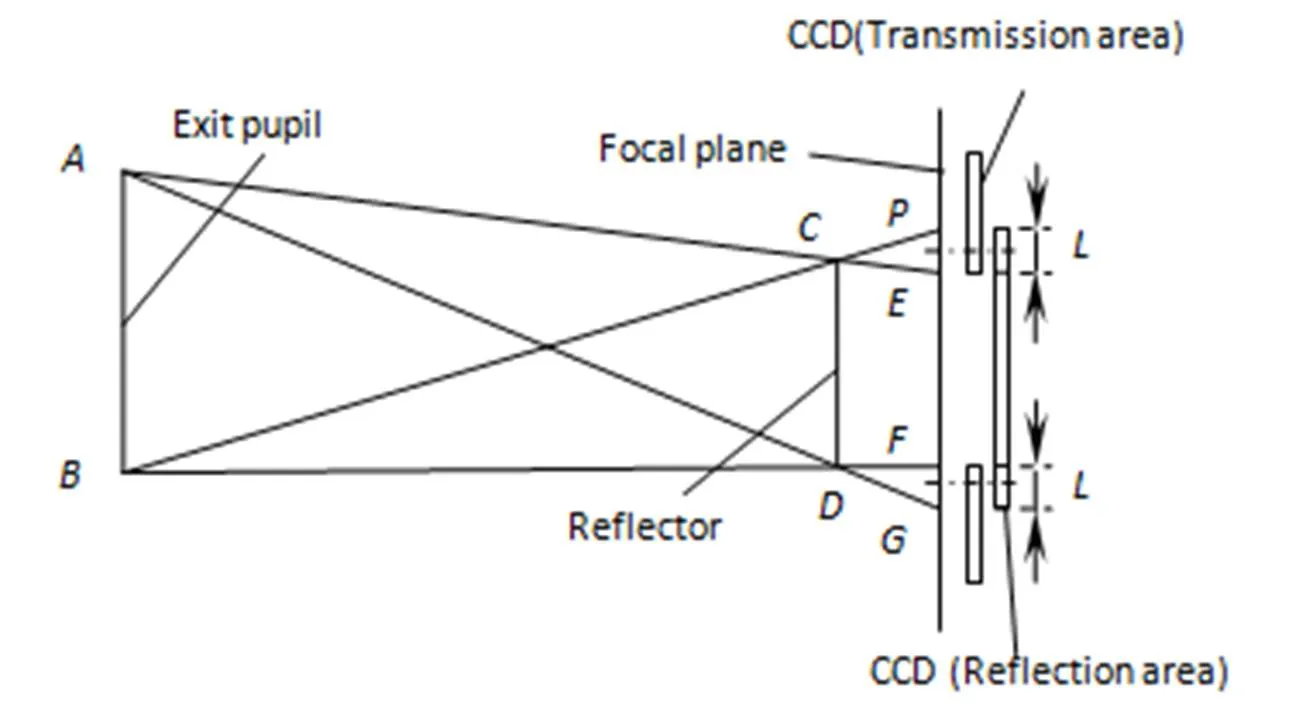
图1 焦面光学拼接模型

图2 焦面光学拼接三维模型

拼接像元数为CCD重叠区内的像元数量，其计算公示为

式中：为拼接像元数，为CCD重叠区长度，为CCD器件像元大小。

由图1可以看出，在进行拼接设计时，需要将透射区和反射区的重叠区中心放置在渐晕区的中心。当CCD重叠区中心偏离渐晕区(或)的中心时，会导致CCD边缘像元的光学传递函数(MTF)严重下降，甚至在CCD成像的像面上出现漏缝现象。

1.2 影响中心重合误差的因素

由以上的分析可知，在实际工程应用中，引起CCD重叠区中心和渐晕区中心不重合的主要原因为通过反射镜边缘的主光线偏离原来位置所致。以下对影响因素进行分析。

1) 拼接反射镜设计及加工误差

如图3所示，在工程应用中，拼接反射镜的设计及加工存在误差(一般可控制在0.1 mm)，当反射镜的误差为1时，通过反射镜边缘的主光线到达像面时会发生偏离，偏离距离为1，即像面上渐晕区中心与理论值的偏差。设拼接反射镜的镜面中心到焦平面(即CCD器件感光面)距离为出瞳距离焦平面距离为，根据几何关系则有：

2) 拼接反射镜装调误差

反射镜在装调时，实际的安装位置与理论设计位置存在一定的安装误差，会导致切割光路的反射镜棱边发生偏移，引起误差的原理与上一项类似，则有

式中：2为拼接反射镜的装调误差，2为通过反射镜边缘的主光线由于反射镜装调误差引起的偏离距离。目前，拼接反射镜装调误差约0.15 mm。

3) CCD拼接误差

CCD拼接时，由于每片CCD的空间拼接位置与理论设计位置存在误差，从而导致CCD重叠区的中心与渐晕区的中心不重合。设CCD沿幅宽方向拼接误差为3，则可知3主要为拼接仪的拼接精度和拼接基准精度所致，此误差一般在0.1 mm以内。

4) 焦面与镜头的对接误差影响

光学拼接的设计基准是将光学系统的主点放置在CCD线阵的中心，由于在定焦过程中定焦误差(本文所指定焦误差为CCD线阵中心沿着线阵方向偏离理论值的误差)的存在，导致焦平面在沿CCD线阵方向发生偏差，从而导致渐晕区的中心与理论发生偏差，设定焦误差为4(一般可控制在0.1 mm左右)，渐晕区中心偏差为4，如图4所示，则根据几何关系有：

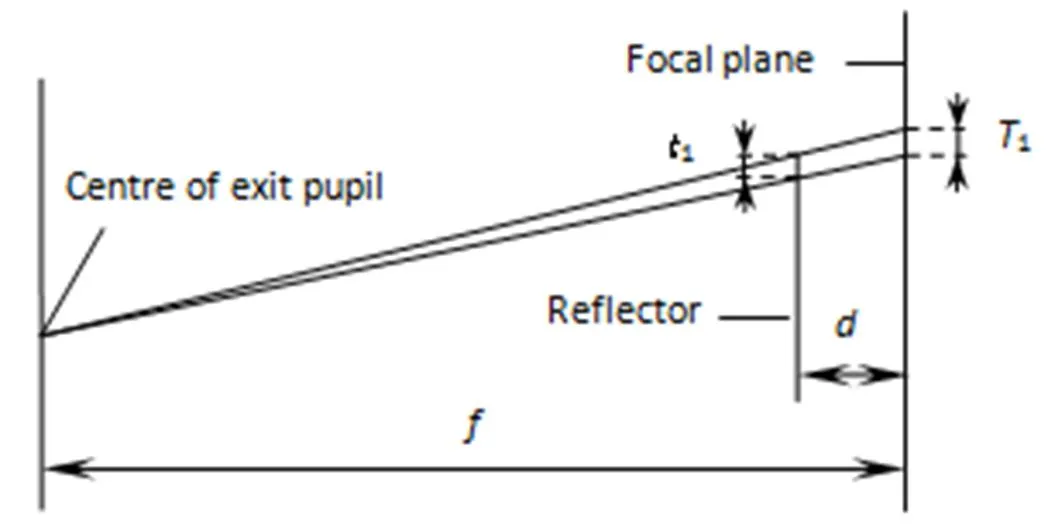
图3 拼接误差模型图

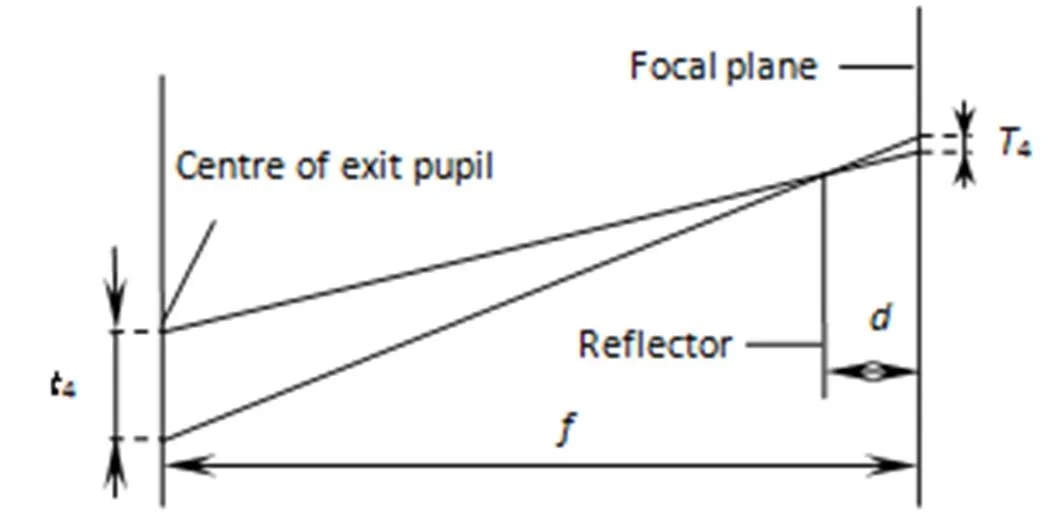
图4 焦面与镜头对接误差模型图

1.3 中心重合误差计算

综合考虑以上所有的误差分析可知，重叠区中心和渐晕区中心不重合误差为

1.4 像方远心及非远心光路的区别

由式(2)(3)(4)可知，当光学系统为远心光路时，即远大于，则有1≈1、2≈1、4≈0。而当光学系统为非远心光路时，即出瞳距较小时，1＞1、2＞2。

以某远心光学系统和某非远心光学系统为例，出瞳距分别为10 100 mm和438 mm，当反射镜距离像面距离都为50 mm，1=0.1 mm，2=0.15 mm，3=0.1 mm，4=0.1 mm，计算结果如表1所示，可以看出非远心光路误差较大，更容易出现漏缝隙现象。

表1 远心光路与非远心光路误差计算结果

2 考虑渐晕区传函下降时重叠像元数的计算

由上述分析可知当重叠像元数大于＞/时，可保证CCD成像时不会导致漏缝现象，另外在拼接时，要考虑渐晕区能量下降引起的传函下降问题[8]，不考虑衍射的情况下，令最大渐晕区==2，出瞳直径为，则有：

对于远心光路有：

式中：#为相机的F数，即相对孔径倒数。

根据图1和图2可知，成像光束会被反射镜切割，切割范围在0~2内变化，使用渐晕系数对拼接区像元的能量(DN值)进行修正，可以对能量的损失进行补偿[8]，但是图像的传递函数会下降。以透射区为例，对渐晕区的传函变化情况进行了计算，如图5所示。横轴为光束切割区域大小(范围0~2)，纵轴为归一化后的传递函数MTF。由图5可以看出，渐晕区的传递函数MTF会随着反射镜切割光束区域的增加而下降，当光束剪切大于1.4时，垂直于飞行方向上的传递函数MTF下降75%左右。

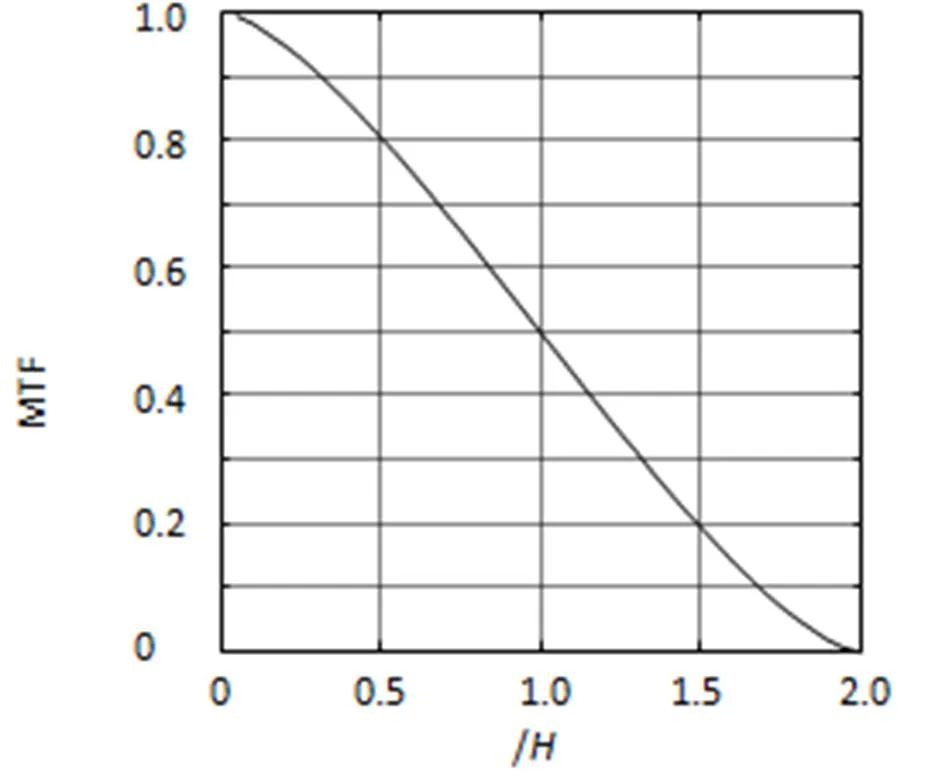
图5 渐晕区传函下降

以渐晕区传函下降不超过75%作为约束条件，并考虑拼接装调误差造成的CCD重叠区中心与渐晕区中心的偏差时，CCD最少重叠像元数min为

对于幅宽有余量的相机，可以将CCD重叠像元数增加，令最大值为max：

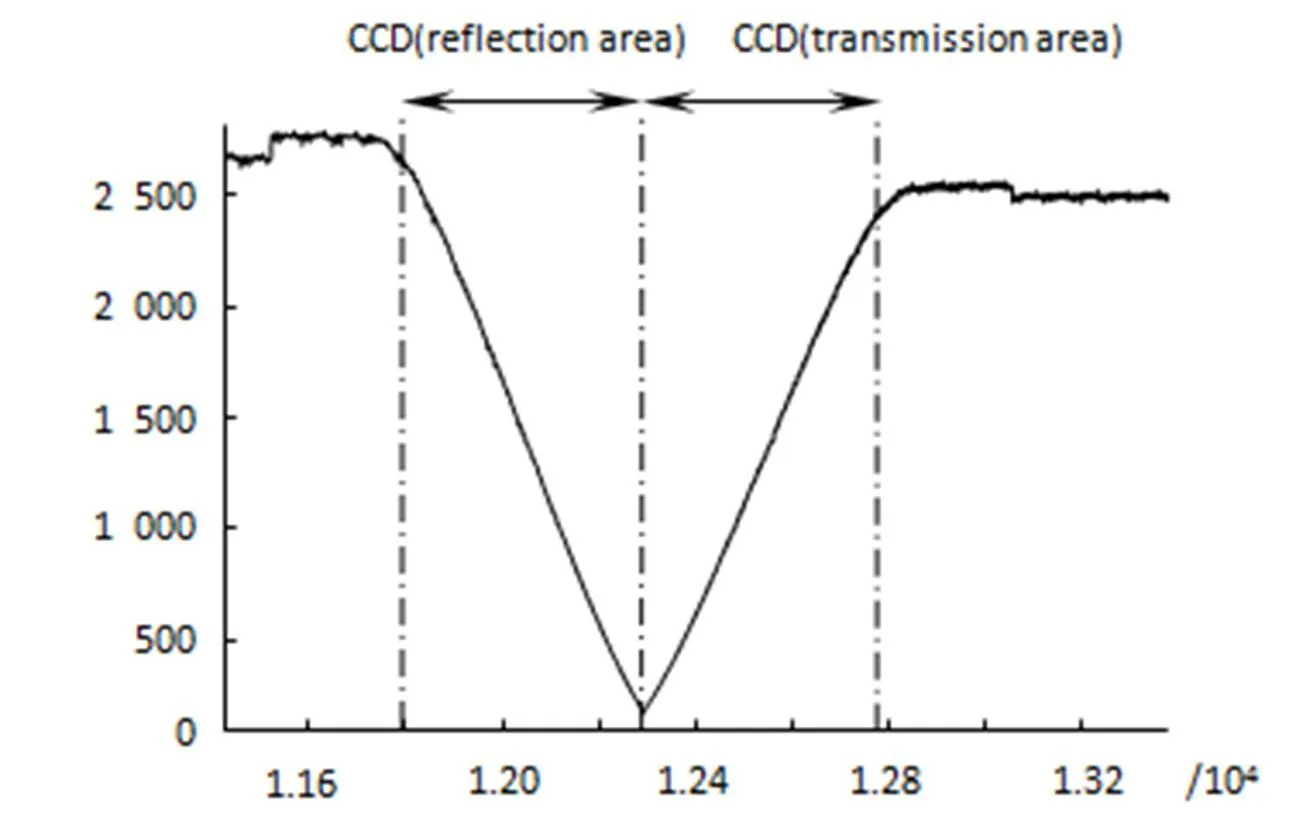
但当取最大值时，CCD边缘的像元位于渐晕区的边缘，接收的能量接近零，图像没有使用价值，故一般情况取

3 实例应用

以某航天相机为例，F数为10，出瞳距=10 230 mm，出瞳直径=1 023 mm，反射镜距离焦平面距离=45 mm，像元大小=0.007 mm，单片器件像元数为12 288；反射镜加工时，公差控制在0.1 mm以内，反射镜装调误差控制在0.15 mm以内，CCD线阵基准误差控制在0.1 mm以内，定焦误差控制在0.1 mm以内。根据式(8)和式(9)则有：

考虑到相机幅宽，在实际拼接时CCD重叠像元数为500个。如图6所示为相机在辐射定标时，相邻2片CCD器件接收的能量分布曲线图(能量叠加前)，图中横坐标为像元数，纵坐标为表征光能量的DN值。从2片CCD器件各自在渐晕区内的能量分布情况分析，拼接不存在漏缝现象，满足图像处理要求。CCD重叠区中心和渐晕区中心重合度误差在40像元以内，与设计值吻合。

图6 辐射定标时CCD搭接区光能分布

结束语

本文首先对光学拼接的特点进行了分析。对于采用反射镜的全反全透式光学拼接焦平面由于CCD重叠区中心和渐晕区中心不重合导致的漏缝现象，对影响中心重合的多个因素进行了定量分析，然后以渐晕区传递函数MTF下降作为约束条件，对CCD重叠像元的最小值和最大值进行了计算公式推导。最后以某航天相机进行了实例应用，通过相机在辐射定标时渐晕区能量变化验证了设计的合理性。

[1] 杨秉新. 国外航天侦察相机和测绘相机发展概况 [J]. 航天返回与遥感，1998，19(2)：16-24.

YANG Bingxin. The development survey of foreign space reconnaissance camera and mapping camera [J]. Spacecraft Recovery & Remote Sensing，1998，19(2)：16-24.

[2] ANTONI R. Progress in focal plane array technologies [J]. Progress in Quantum Electronics(S0079-6727)，2012，36(2/3)：342-473.

[3] 郭疆，龚大鹏，朱磊，等. 测绘相机焦平面CCD交错拼接中重叠像元数计算 [J]. 光学精密工程，2013，21(5)：1251-1257.

GUO Jiang，GONG Dapeng，ZHU Lei，Calculation of overlapping pixels in interleaving assembly of CCD focal plane of mapping camera [J]. Optics and Precision Engineering，2013，21(5)：1251-1257.

[4] 何昕，魏仲慧，郝志航. 基于单心球面系统的九块面阵CCD数字拼接 [J]. 光学精密工程，2003，11(4)：421-424．

HE Xin，WEI Zhonghui，HAO Zhihang. Digital camera modeling of butting 9 CCD chips in the concentric spherical lens system [J]. Optics and Precision Engineering，2003，1l(4)：421-424．

[5] 徐彭梅，杨桦，伏瑞敏，等. CBERS-l卫星CCD相机的光学拼接，配准和定焦 [J]. 航天返回与遥感，2001，22(3)：12-15．

XU Pengmei，YANG Hua，FU Ruimin，. Optical butting，registration and focus-fixing of CCD camera for CBERS-l satellite [J]. Spacecraft Recovery & Remote Sensing，2001，22(3)：12-15.

[6] 何凯，唐平凡，王成忧. 基于高斯曲面拟合的影像渐晕复原方法 [J]. 电子学报，2009，37(1)：67-71.

HE Kai，TANG Pingfan，WANG Chengyou. Vignetting correction method of image based on gaussian quadrics fitting [J]. Actaelei：Tronicasinica，2009，37(1)：67-71.

[7] 王伟，李林. 反射式光学像面拼接方法研究 [J]. 光子学报，2014，43(3)：80-86.

WANG Wei，LI Lin. Reflector Mirror Based Optical Butting [J]. Acta Phontonica Sinica，2014，43(3)：80-86.

[8] 陶明慧. 基于反射镜拼接的图像渐晕处理技术研究 [D]. 长春：中国科学院长春光学精密机械与物理研究所，2012：10-13.

TAO Minghui. Research on the Vignetting Correction Method of Mosaic Images based on Reflector [D]. Changchun：Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，2012：10-13.

Calculation of Overlapping Pixels in Focal Plane Based on Optical Butting

CHU Bei，LI Fuqiang，CHANG Junlei

( Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)

In order to eliminate the imaging gap of focal plane based on optical butting, an error analysis-based algorithm of overlapping pixels was proposed. Firstly, an imaging model for focal plane based on optical butting is established according to the imaging principle of camera. Then, the reason causing imaging gaps is analyzed which combined with telecentric and non-telecentric optical system. Combined with the decrease of MTF in the vignetting distortion caused by the reflector, the formula for computing the numbers of overlapping pixels between adjacent CCDs is obtained. Finally, an example is given. Experimental results show that the proposed algorithm can eliminate the imaging gap.

optical butting; focal plane; overlapping pixels; imaging gap

1003-501X(2016)12-0099-05

TP732

A

10.3969/j.issn.1003-501X.2016.12.016

2016-04-27；

2016-07-23

褚备(1984-)，男(汉族)，辽宁抚顺人。工程师，硕士，主要从事光学遥感器光机结构设计工作。E-mail：chubei1984@163.com。