矩形孔径主动自由曲面变形数据拟合

周 超，邢廷文



矩形孔径主动自由曲面变形数据拟合

周 超，邢廷文

( 中国科学院光电技术研究所，成都610209 )

折反式深紫外光刻物镜采用反射镜为主动自由曲面，补偿系统热像差。一些物镜系统要求反射镜的通光孔径为矩形。出于描述反射镜主动变形的目的，需要采用矩形区域正交的多项式拟合变形数据。高精度的拟合要求需要获得高阶的多项式表达式。本文根据正交多项式的性质，推导了矩形正交多项式的通式并列出前36项多项式的表达式。应用该多项式对主动自由曲面的变形数据进行拟合。结果表明，变形均方根值(RMS)在2 nm~5 nm范围内，最小拟合残差可达0.024 nm。根据拟合残差面形的特点，可以对主动自由曲面的结构设计改进。

Zernike多项式；矩形孔径；正交多项式；折反射式光刻物镜

0 引 言

光刻机是大规模集成电路制造的核心设备，也是最复杂精密的光学系统之一[1]。掩模、镜片甚至空气因热效应引起的像差都会降低电路图案的曝光质量。因此，热像差主动补偿是目前光刻机研制的关键技术之一。一种可行的技术路线是将光刻物镜中的反射元件改造为可主动变形的主动自由曲面，从而实现多模式像差补偿[2]。

像差补偿原理是主动自由曲面产生与波像差等量相反的变形而消除像差。在主动补偿过程中，像差以Zernike模式系数的形式在程序数据流中出现。因此要求镜面的面形也采用模式系数表示。而折反射式深紫外光刻物镜中，其反射镜通光孔径为矩形[3]。为满足这类光刻物镜的高精度补偿热像差的要求，需要一种在矩形区域正交且与光学模式匹配的多项式用于面形数据拟合。

早在1981年Mahajan应用Gram-Schmitt正交化方法，基于圆Zernike多项式推导了一系列的环形区域正交多项式[4]。后续研究者按照该方法完成了对六边形孔径[5]、矩形孔径[6-8]、方形孔径和狭缝[9]的部分正交多项式推导。然而该方法是一种递推的方法：在已知前项表达式的基础上，需要进行次积分运算方可获得第+1项。多项式级次越高，表达式越复杂而计算量也越大。因此文献[6]，[7]和[8]中分别仅计算出了多项式的前9项、前15项以及前21项。目前光刻物镜要求对前36项Zernike模式像差补偿，未来的要求是满足前64项Zernike模式像差或更高的补偿要求[10]。目前矩形孔径高阶变形表达方法是采样点上正交向量替代正交多项式用于拟合[11]。该方法存在拟合精度受残差干扰和拟合结果受采样点影响的缺点。当前的研究结果无法满足高精度拟合镜面面形的要求。因此，获取矩形孔径正交多项式的通式表达式有利于高阶像差的表达，从而获得对镜面的高精度拟合。

1 光刻物镜中的主动自由曲面

常见的主动补偿元件，如变形镜、主动镜，是圆形孔径。本文针对光刻物镜的应用环境，主动补偿器件的通光孔径是矩形孔径。图1为来自文献[3]的工作波长193 nm深紫外光刻物镜。它采用折反射结构，像方数值孔径为1.35。第24和25光学面为反射镜面。光刻物镜的有效视场为100 mm×25 mm的矩形范围。追迹光路两次通过面24的位置：第1次是由物体发出的光经过面24反射，获得通光孔径区域；第2次是由面25反射到像面的光经过面24位置，获得不可遮挡的透光区域。如图2(a)所示，下方矩形区域为通光区域，上方矩形区域为透光区域。表1列出了两区域的边界坐标。

图1 深紫外光刻物镜模型

表1 反射镜24的通光孔径和透光区域

从表1中列出的数据，可以计算出基于反射面24的主动自由曲面孔径为250 mm´84.4 mm的矩形区域。主动自由曲面由排布在镜面背后的促动器作用实现镜面的主动变形，其结构模型如图2(b)所示。根据热像差的特性，控制促动器阵列产生对应的镜面变形从而补偿像差。

图2 (a) 反射面24的通光(下矩形)和透光区域(上矩形)；(b) 基于反射面24的主动自由曲面结构模型

2 矩形孔径正交多项式

主动自由曲面的变形模式要与热像差模式一致，变形的描述需要一组与像差对应的多项式。光学像差与Zernike多项式相对应。而Zernike多项式数学上是一组二维泰勒多项式。若矩形孔径正交多项式由二维泰勒多项式构成，则可与光学像差保持关联。因直角坐标系比极坐标系在描述矩形区域更方便，故将矩形上正交的多项式记为。在图3所示单位正方形区域{(,)|0≤≤1, 0≤≤1}中，多项式正交则满足：

图3 单位方形区域

其中a表示R()中t的系数。R()需要满足正交关系：

将矩形正交多项式S(，)用R()构成为

则S(，)必然满足式(1)，是矩形区域正交的多项式。于是推导矩形区域正交的多项式的问题归结为求解R()的表达式。

将式(5)代入式(4)，得到R()系数方程组。由(+1)/2个方程组成：

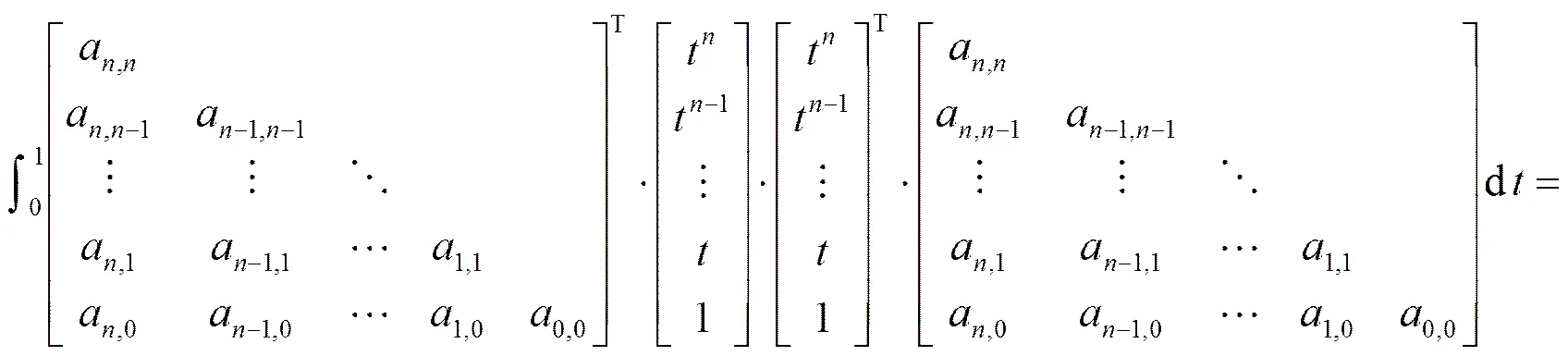
得到的系数表达式：

将上式和式(4)带入到式(6)，得到矩形区域的正交多项式表达通式：

式(9)所表示的多项式在图3所示单位正方形区域上具有正交特性。通过坐标变换可以扩展到任意矩形区域范围内正交，这表明矩形区域正交多项式可以与经典的圆Zernike多项式一样，可由通式经过简单计算得到某项表达式，而不需按照文献[6]和[7]中的方法，从低阶项递推到高阶项，也不需如文献[8]和[9]中对多项式进行数值近似求解而简化表达式，而且不同于参考文献[6-9]中的多项式表达式随拟合区域尺寸改变而需重新计算，本文提出的多项式只需简单的坐标变换就满足不同尺寸矩形区域。该多项式与圆Zernike多项式一样是完备的二维泰勒多项式，能满足光刻物镜中对高阶像差表达的需求。本文提出的多项式具有项数多、应用方便和拟合精确的优点。表2中列出了前36项矩形区域正交多项式的表达式。

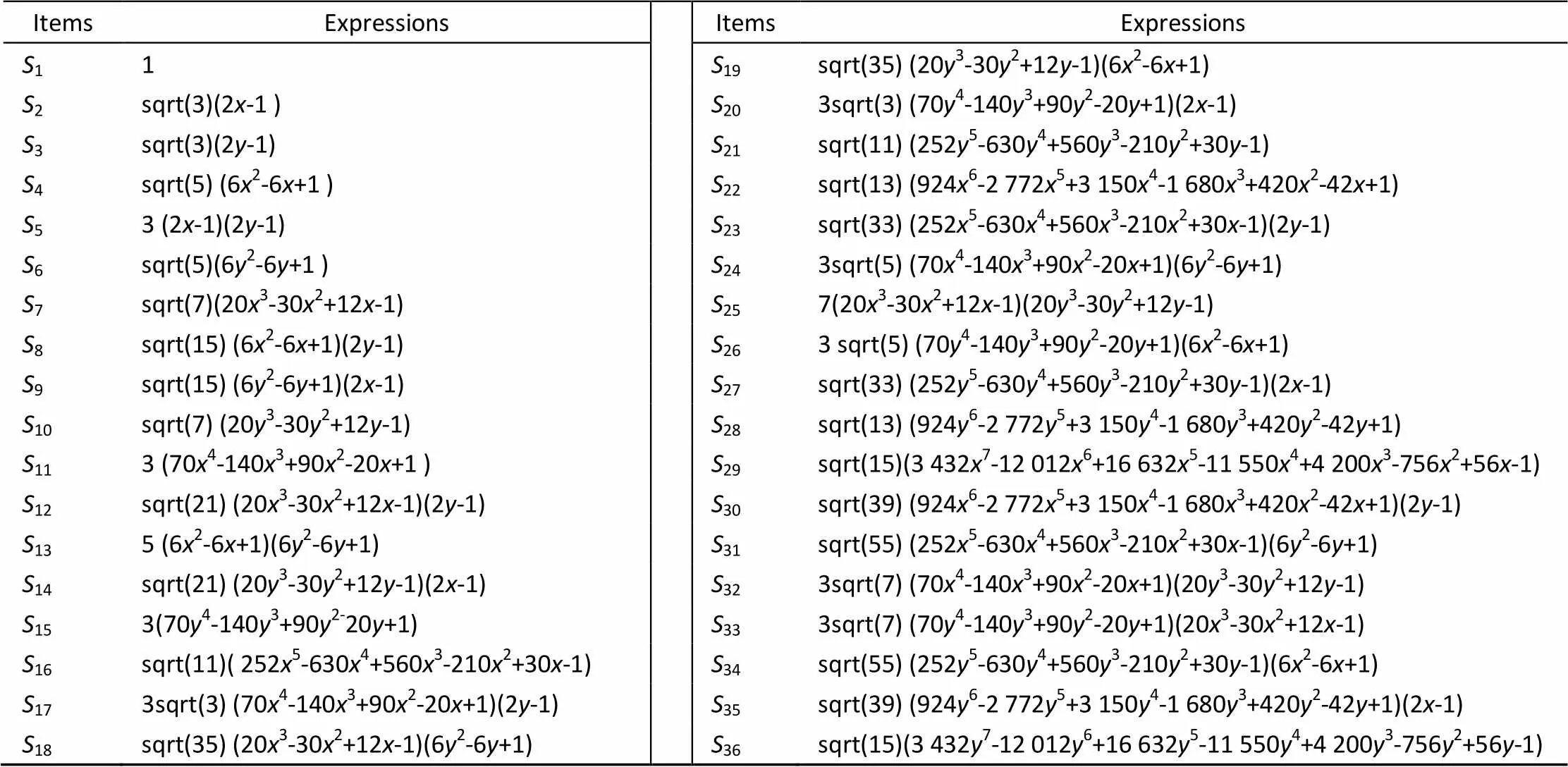
表2 矩形区域正交多项式

注：

3 矩形孔径面形数据拟合结果

193 nm光刻物镜需补偿的热像差通常PV值小于25 nm，RMS在2 nm~5 nm范围。在此考虑前36阶Zernike像差补偿。用上述正交多项式在Matlab中拟合补偿不同热像差时的主动自由曲面面形。受篇幅限制，图4~图6仅列出表3中前3种情形下的主动自由曲面面形，本文36项多项式拟合结果和文献[7]多项式拟合结果。三组图中：图(a)为主动自由曲面面形，图(b)为本文推导的多项式拟合面形结果，图(c)为本文多项式拟合残差，图(d)为参考文献[7]列出的多项式拟合面形结果，图(e)为参考文献[7]多项式拟合残差。

表3中归纳了10组面形的拟合结果比较。本文多项式在多数情形下拟合残差RMS小于0.1 nm，能够满足高精度的拟合面形数据的要求。情形3的拟合残差RMS为0.32 nm，表明该结构的主动自由曲面对情形3热像差的补偿能力稍差。所有情形中本文多项式拟合精度都优于文献[7]所列的多项式拟合精度。

图4 情形1的面形数据拟合结果

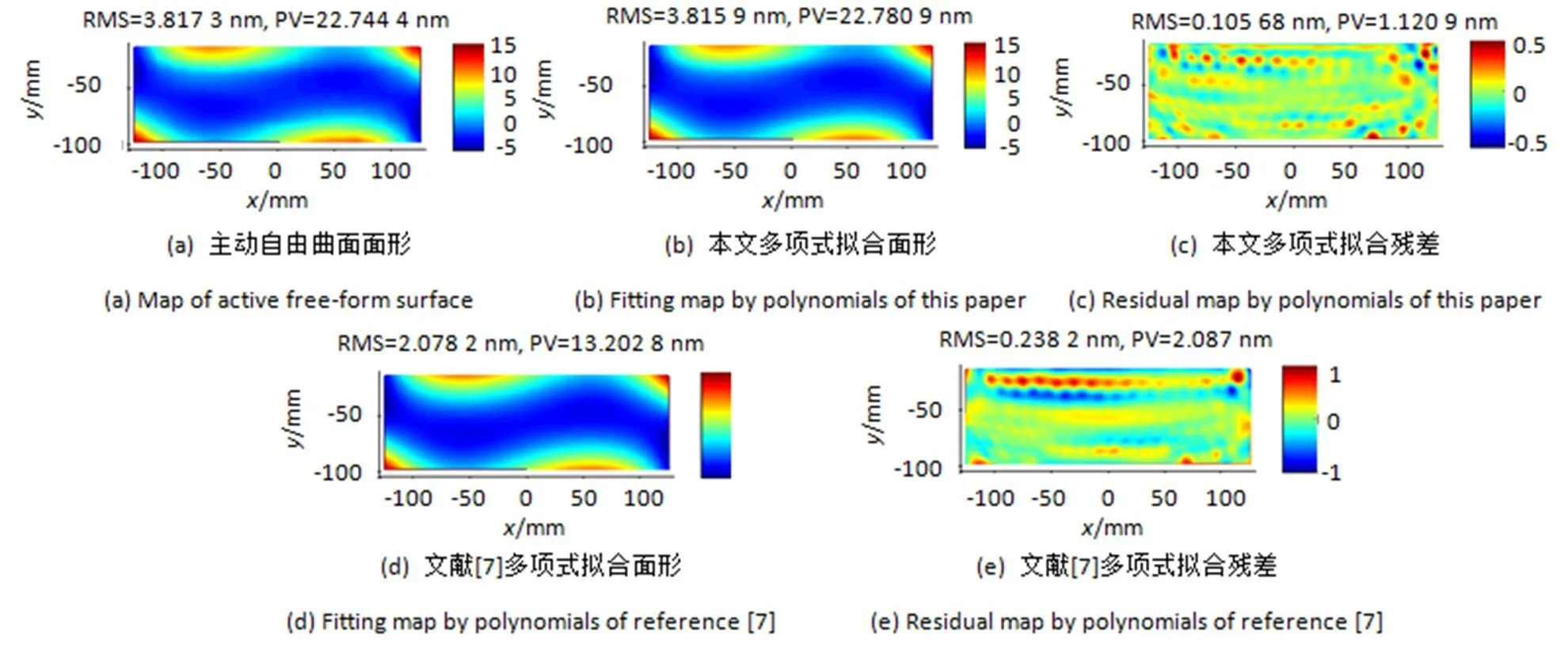
图5 情形2的面形数据拟合结果

图6 情形3的面形数据拟合结果

表3 10组面形的拟合结果比较

高精度拟合镜面面形的残差为图4(c)、图5(c)以及图6(c)显示的斑点状图案。这是促动器在该处推拉镜面所产生的尖锐变形，表现为高于36阶的模式面形。残差图指示了这些不被期望出现的高阶变形的位置。从情形3的残差图6(c)可了解到，较多的高阶面形出现在镜面下部左右对称的两块区域。在主动自由曲面设计过程中，通过对该区域促动器数量增加和分布优化可降低高阶面形量来提高主动自由曲面补偿性能。但在面形拟合精度不够高时，如残差图6(e)中，促动器导致的尖锐变形被部分低阶模式掩盖而不能提供指导作用。

4 结 论

本文针对光刻物镜热像差补偿的应用中的需求，通过数学推导得到矩形区域正交多项式的通式表达式并列出了前36项多项式的具体表达式。相比于其他研究者，本文的正交多项式表达式计算更容易、列出项数更多。在面对高阶像差拟合的需求问题，可通过增加正交多项式项数，提高对矩形孔径面形表示的精度。运用该多项式对10组不同的镜面变形数据拟合表达，从结果看变形RMS在2 nm~5 nm范围内，多数情形拟合残差小于0.1 nm，最小拟合残差RMS可达0.032 nm。拟合结果能够准确的描述矩形镜面的变形。而且残差图显示了主动自由曲面变形的高阶变形区域，能指导其结构优化设计。

[1] Matsuyama Tomoyuki，Ohmura Yasuhiro，Williamson David M. The Lithographic Lens：its history and evolution [J]. Proceedings of SPIE(S0277-786X)，2006，6154(615403)：1-14.

[2] WANG Yueqiang，LIU Yong. Research development of thermal aberration in 193 nm lithography exposure system [J]. Proceedings ofSPIE(S0277-786X)，2014，9283(928314)：1-8.

[3] 朱红伟，邢廷文. 一种高数值孔径浸没投影物镜：中国，201310325062.5 [P]. 2013.

[4] Mahajan Virendra N. Zernike annular polynomials for imaging systems with annular pupils [J].Journal of the Optical Society of America(S0030-3941)，1981，71(1)：75-85.

[5] Mahajan Virendra N，DAI Guangming. Orthonormal polynomials for hexagonal pupils [J]. Optics Letters(S0146-9592)，2006，31(16)：2462-2464.

[6] HE Pinjiang，ZONG Xiaoying，FU Ruimin. Zernike polymomials for rectangular area and applications in off-axis asphere testing [J]. Proceedings ofSPIE(S0277-786X)，2010，7656(765615)：1-6.

[7] 廖志远，邢廷文，刘志祥. 矩形孔径上折射率均匀性数据拟合研究 [J]. 光电工程，2011，38(11)：146-150.

LIAO Zhiyuan，XING Tingwen，LIU Zhixiang. Fitting of Index Homogeneity Data on the Rectangle Pupil [J]. Opto-Electronic Engineering，2011，38(11)：146-150.

[8] Ali Hadi Al-Hamdani，Sundus Y Hasan. Zernike polynomials for optical systems with rectangular and square apertures of area equal to Pi [J]. Indian Journal of Pure & Applied Physics(S0019-5588)，2013，51(1)：837-843.

[9] Mahajan Virendra N，DAI Guangming. Orthonormal polynomials in wavefront analysis：analytical solution [J]. Journal of the Optical Society of America A(S1084-7529)，2007，24(9)：2994-3016.

[10] Staals Frank，Andryzhyieuskaya Alena，Bakker Hans，. Advanced wavefront Engineering for Improved Imaging and Overlay Applications on a 1.35 NA Immersion Scanner [J]. Proceedings ofSPIE(S0277-786X)，2011，7973(79731G)：1-13.

[11]YE Jingfei，LI Xinhua，GAO Zhishan，. Modal wavefront reconstruction over general shaped aperture by numerical orthogonal polynomials [J]. Optical Engineering(S0091-3286)，2015，54(3)：419–427.

Deformation Data Fitting of Active Free-form Surface with Rectangular Aperture

ZHOU Chao，XING Tingwen

( Institute of Optics and Electronics, Chinese Acadmy of Science, Chengdu 610209, China )

Catadioptic deep ultraviolet lithography objective took the mirror as active free-form surface to compensate thermal aberration. Mirror in compliance with the requirements of the system optical path had a rectangular aperture. For the purpose of describing the active deformation of mirror, it’s necessary for orthogonal polynomials in rectangle zone to fit the deformation data. For high accuracy of fitting surface deformation, it was needed to obtain higher order polynomial expressions. According to the properties of orthogonal polynomials, rectangular orthogonal polynomials formula was derived and the first 36 polynomial expressions were listed. And the polynomials were applied to fit the deformation data of active free-surface. The results showed that the minimum fitting residual error RMS is 0.024 nm when the deformation is 2 nm~5 nm in RMS. According to the characteristic of fitting residual map, the structure design of the active free surface could be improved.

Zernike polynomial; rectangle pupil; orthogonal polynomial; catadipotric lithography objective

1003-501X(2016)12-0104-06

O435.2；O439

A

10.3969/j.issn.1003-501X.2016.12.017

2016-05-03；

2016-05-12

周超(1989-)，男(汉族)，湖北武汉人。博士研究生，主要研究工作是光学系统像差补偿。E-mail: gxmarble@163.com。