瑞利阻尼对砂土场地非线性地震响应的影响分析

王 豪, 高广运, 杨成斌

(1.同济大学岩土及地下工程教育部重点实验室,上海 200092; 2.同济大学地下建筑与工程系,上海 200092;3.合肥工业大学资源与环境工程学院,安徽 合肥 230009)

瑞利阻尼对砂土场地非线性地震响应的影响分析

王 豪1,2, 高广运1,2, 杨成斌3

(1.同济大学岩土及地下工程教育部重点实验室,上海 200092; 2.同济大学地下建筑与工程系,上海 200092;3.合肥工业大学资源与环境工程学院,安徽 合肥 230009)

在地震荷载作用下,自由场地会产生土体侧向变形和地表响应放大现象。由于土体的高度非线性,计算自由场地地震响应时,不同的阻尼比及剪切模量取值是造成其计算结果与试验结果相差较大的原因之一。目前动力计算常采用瑞利阻尼方法,其系数取值会在一定程度上影响计算结果。选用两模态简化瑞利阻尼系数计算方法,分析土体阻尼比及控制频率的取值对计算结果的影响,对比离心机模型试验,利用开源有限元平台OpenSees,采用适合于土体动力分析的多屈服面本构模型(PDMY),建立剪切梁模型模拟三维自由场地,并分析瑞利阻尼参数对自由场地地震响应和侧向变形计算结果的影响。结果表明,针对相对密度为60%的Nevada干砂,阻尼比为4%、控制频率比为5时,场地响应计算结果与试验结果较为符合。综合分析显示场地非线性响应时域计算时,应特别注意选用的瑞利阻尼参数值。

地震响应; 侧向变形; 阻尼比; 瑞利阻尼系数; 离心机试验; OpenSees

0 引言

自由场地的动力响应计算问题一直是岩土地震工程中具有理论和实际意义的研究课题。在自由场地土层地震响应分析的研究和工程应用中主要有两种分析方法,即频域分析和时域分析。地震反应分析方法起初主要是Seed等编写的SHAKE程序,其运用等效线性化方法在频域内对场地的地震反应进行一维分析[1]。由于地震动特性复杂、土体的高度非线性以及动力计算问题等多因素的影响,过去多采用简化方法进行评估。实际工程中等效线性化分析方法缺点较多,吴世明[2]、栾茂田[3]认为等效线性化模型不能真实反映土体非线性对地震反应的实际影响。土体具有高度非线性,在动力分析时剪切模量会随着剪应变的增大而减小,阻尼随着剪应变的增大而增大[4]。因此在进行非线性地震响应分析时,土体剪切模量衰减关系及阻尼的选取对其计算结果影响较大。

阻尼反映材料的减震耗能能力,是土体动力计算的重要影响因素之一。不同材料的阻尼与其物理特性和分析方法等密切相关,工程实际中常采用简化的数学模型进行计算。在土层地震反应分析中,频域分析常采用滞后阻尼模型,通过等效线性化方法来模拟土体的非线性特性,滞后阻尼是不依赖于频率的参数;而在进行时域分析时,通常采用瑞利阻尼计算方法的黏滞阻尼,而瑞利阻尼是频率相关的。其阻尼矩阵有全瑞利阻尼、两模态简化瑞利阻尼和四模态扩展瑞利阻尼等不同的表达式[5]。目前在进行时域动力分析时常采用简化瑞利阻尼,黏性阻尼矩阵与频率相关。因此控制频率的选取对于阻尼的影响以及动力计算的精确性需要特别注意。

目前,自由场地地震反应非线性分析通常采用时域逐步积分,而常用计算程序如DeepSoil、OpenSees等均采用瑞利阻尼模型,因此合理选取阻尼系数对提高场地响应评估的精确性是十分必要的。本文对不同阻尼比值和控制频率参数进行分析,并通过不同地震动计算结果对所选取参数进行评价,分析其与瑞利阻尼相关系数的取值对于自由场地地震响应和侧向变形模拟精确性的影响。

1 瑞利阻尼系数计算方法

动力计算采用的运动方程形式为:

(1)

Ce=αMe+βKe

(2)

式中:α 和β 均为阻尼系数。阻尼比 ξ 表示为:

(3)

式中:圆频率ω=2πf,ξ由阻尼比与剪应变关系曲线确定。式(3)表明阻尼和频率是相关的,但实际土体阻尼与频率无关,因此α和β取值需在计算时使阻尼值在有效频率范围内,且与实测的阻尼比较接近。

HUDSON等[6]对瑞利阻尼系数进行改进,确定了较为精确的瑞利阻尼系数取值方法,在QUAD-4M计算程序中采用该方法与频域分析程序SHAKE-91 计算结果进行比较,二者的结果相近。此方法利用ω0和ωn两个频率来确定α和β,ω0为计算模型基频,ωn=nω0(n 为奇数)且大于地震波主频,则α和β的计算式为:

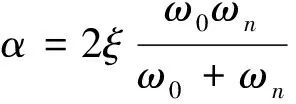
(4)

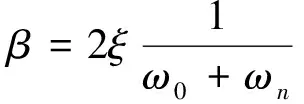
(5)

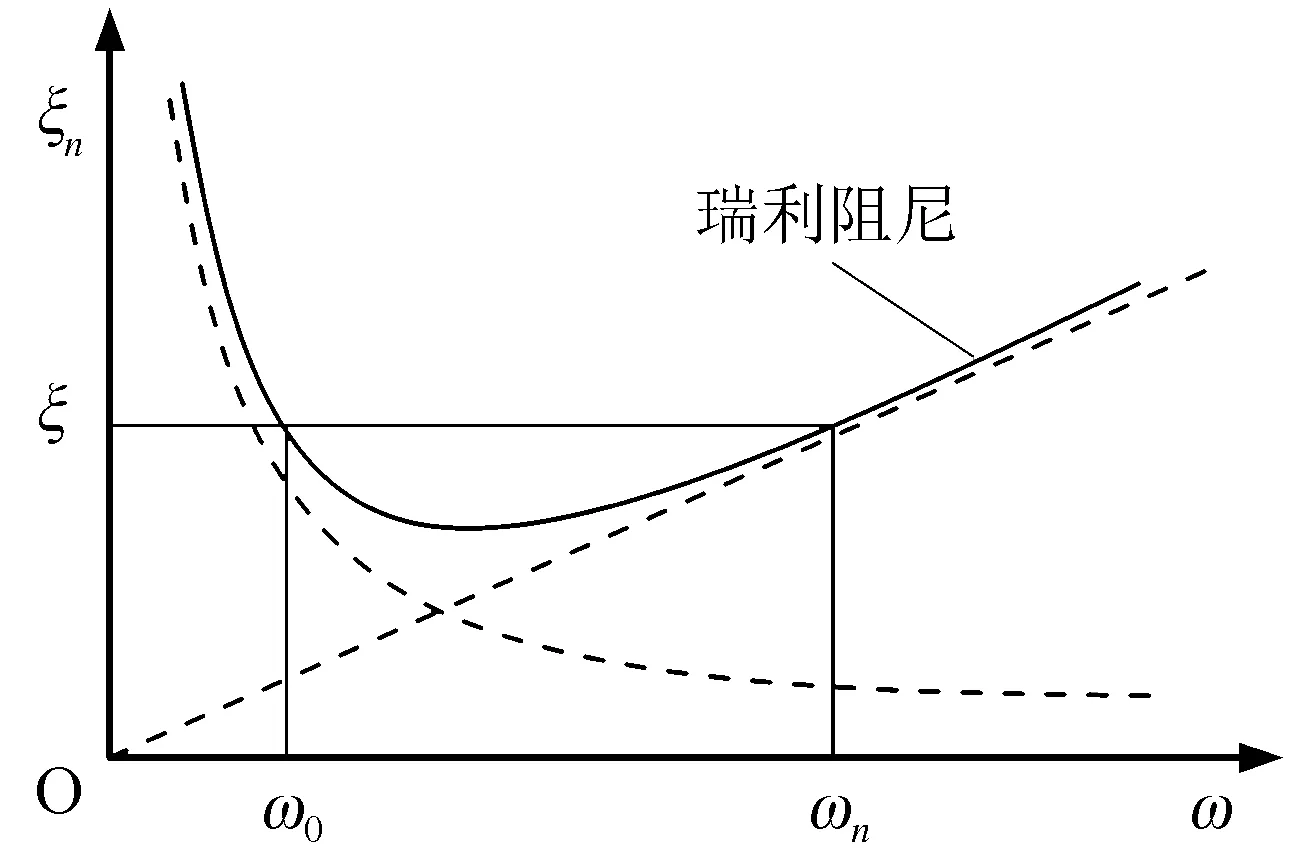
图1 瑞利阻尼与实际阻尼的关系Fig.1 The relationship between Rayleigh damping and actual damping

对于一维场地反应分析时,通常采用下式确定场地基频:

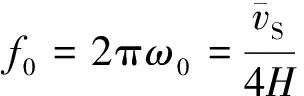
(6)

2 离心机模型试验

本文基于Hashash等[8]对Nevada干砂的离心机振动台试验,建立对应的一维自由场地原型进行模拟计算。试验所采用土体为相对密度接近60%的Nevada干砂,共选取6组不同地震波输入情况下的试验工况,利用加速度和位移传感器测定不同深度处加速度及侧向变形时程。

本文计算模型仅选用其中两种工况进行对比,所采用工况的输入地震为Loma Prieta波(峰值加速度0.33g)和Kobe波(峰值加速度0.76g),地震数据来自强震数据中心[7]。两组地震时程曲线如图2所示。

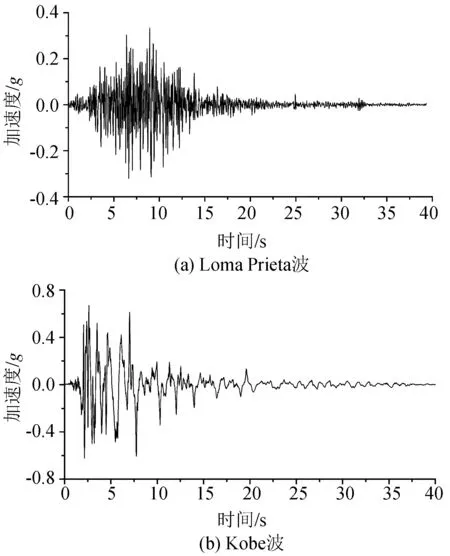
图2 两组地震波时程Fig.2 Acceleration time-histories of two seismic waves

3 有限元模型建立及参数选取

本文采用OpenSees开源有限元程序进行数值模拟,通过上述离心机模型试验所对应的场地原型建立有限元模型。

自由场地在水平方向对称,因此建立有限元网格模型如图3(a)所示。该模型土层厚度26 m,共21个单元。单元类型均为Brick,共有两种单元尺寸:土层深度0～16 m范围内采用1 m的竖向尺寸,16～26 m范围内采用2 m的竖向尺寸。底面节点约束各方向自由度,固定在基岩上,同层四个节点将其三个方向的自由度利用EqualDOF命令等效绑定。计算本构采用PDMY模型(适合于砂土数值模拟的动力计算),选取参数参考Hashash等[8]和OpenSees使用手册中Mazzoni等[9]的建议值,具体如表1所列。

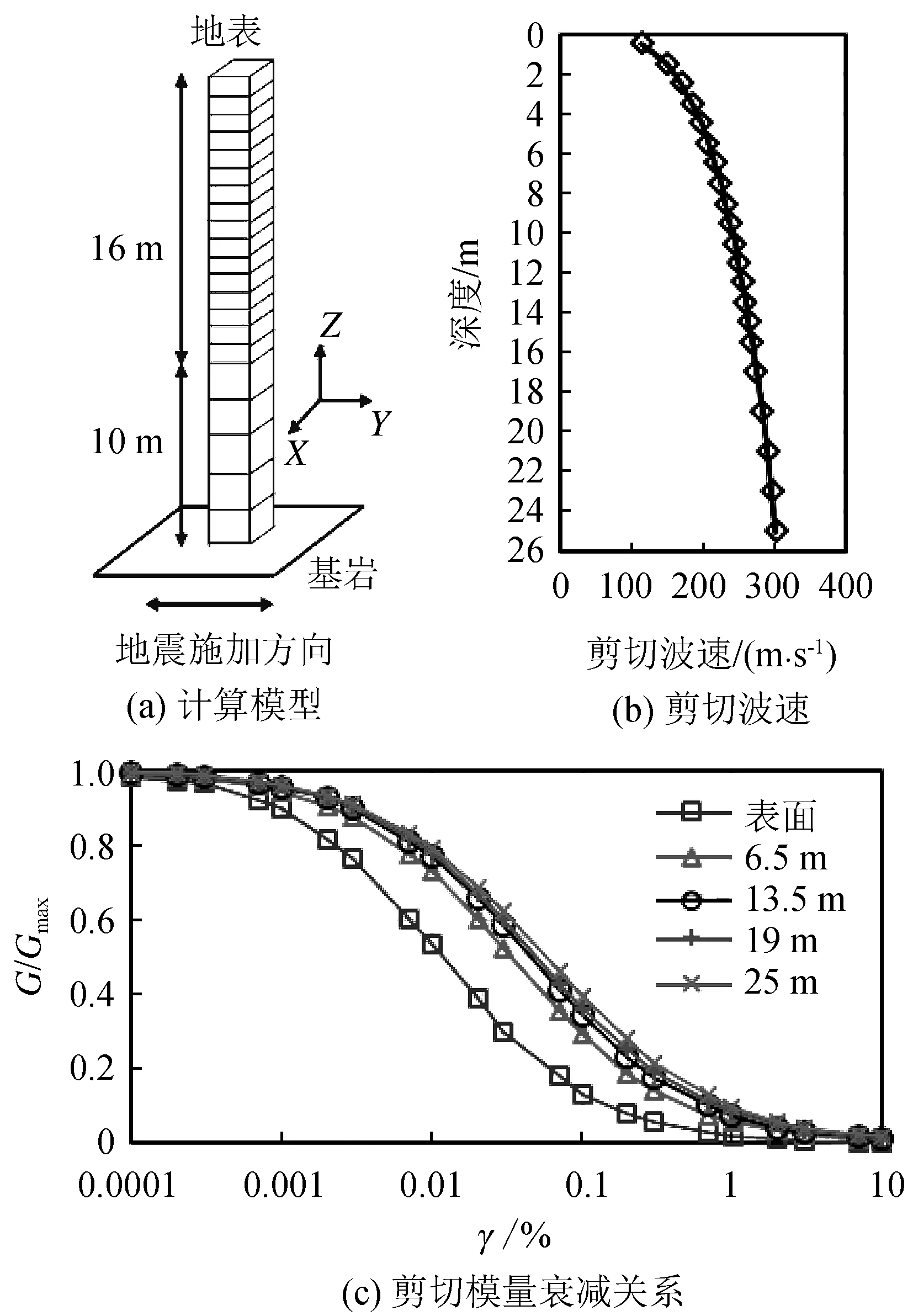
图3 计算模型及参数Fig.3 The calculation model and parameters

密度r/(g·cm-3)泊松比μ平均围压p’r/kPa围压系数/np内摩擦角φ/(°)峰值剪应变γmax/%相位转换角ΦPT/(°)初始孔隙比e接触参数c剪胀参数d1d2液化参数l1l2l31．560．31800．5331026．50．6920．050．62100．0151

为充分考虑土层非线性对地震反应分析的影响,本文考虑土体剪切波速随深度变化以及不同深度处的土体剪切模量随剪应变的衰减关系不同[图3(b)、(c)],利用式(7)计算场地不同深度剪切模量和体积模量,场地基频f0由式(6)求得。

Gmax=vSρ2

(7)

数值计算分析包括固结分析和地震荷载动力响应分析两个阶段。首先施加重力得到地基初始应力场,然后输入地震动进行动力计算分析。

4 模拟结果与分析

首先利用地震动强度较小的Loma Prieta波作为输入地震波,对比分析小应变阻尼比ξ和控制值频率比n取值不同对于计算结果与离心机试验结果的影响,确定最接近实测结果的ξ和n值。然后利用峰值加速度较大的Kobe波作为输入地震波,选用已经确定的ξ和n值作为计算参数,对比分析土体在大震下应变较大时地震反应计算的精确性。

4.1 不同阻尼比取值的影响分析

图4表示在Loma Prieta波作用下,阻尼比ξ分别取1%、2%、3%、4%和5%,控制频率比值按照Phillips[10]建议的n=5时,土层最大水平位移、最大剪应变和峰值加速度随深度变化计算值和离心机实测结果的对比,以及地表阿里亚斯强度曲线和加速度反应谱与实测结果的对比分析。

图4 不同阻尼比条件下计算值与试验值对比(n=5,Loma Prieta波)Fig.4 Comparison between calculated and experimental values with different damping ratio (n=5,Loma Prieta)

图4(a)中,正向最大水平位移计算值均比离心机实测值略大,而负向的计算值则均比离心机实测值略小。同离心机实测值一样,正、负向水平位移最大值随深度增加逐渐减小。随阻尼比ξ增大,同一深度处正、负向水平位移略有增大。地表负向最大位移在2 cm左右,正向最大位移在3 cm左右。

图4(b)中,土层各深度处最大剪应变值均在0.1%左右,深度较浅处略有增大,说明土层震动过程中处在较小应变水平,计算结果均较为精确。同一深度处,随阻尼比ξ减小土体剪应变逐渐增大,表明阻尼比值越大地震波能量消散越快,而土层最大侧向位移和最大剪应变有所减小。

图4(c)表明干砂土层存在场地放大效应,且阻尼比越小同一深度处峰值加速度越大,放大效应越明显。同输入地震动峰值加速度0.33g相比,阻尼比ξ取1%～5%对应的地表峰值加速度计算值放大倍数分别为1.02、1.18、1.41、1.59和1.76,试验值放大倍数为1.31。

图4(d)中,阿里亚斯强度时程曲线在上升过程中,试验实测值整体低于计算值。同样由于阻尼对于地震波能量在土层传播过程中的消耗作用,阻尼比取值1%～5%,阿里亚斯强度最终值分别为9.45、8.24、7.68、7.14和6.05 m/s,呈逐渐减小趋势;试验值为7.13 m/s。图4(e)中,地表加速度反应谱不同时阻尼比计算结果相差不大,均在0.2～0.5 s 有明显的放大效应,说明地震波短周期成分占主要地位。

综合分析图4,与离心机试验实测值相比,固定两控制频率比n=5条件下,阻尼比ξ在计算中取4%时相对较为精确,尤其在图4的最大水平位移、最大剪应变和峰值加速度的对比中较为明显。

4.2 两控制频率比值n取值不同时的影响分析

图5表示在Loma Prieta波作用下阻尼比ξ取4%、控制频率比分别取3、5和7时,数值计算结果和离心机实测结果的对比。

图5 不同控制频率比条件下的计算值与试验值对比(ξ=4%,Loma Prieta波)Fig.5 Comparison between calculated and experimental values with different control frequency ratio (ξ=4%,Loma Prieta)

图5(a)中,土层侧向最大位移变化同图4(a)规律一致,且随频率控制比n增大同一深度处正、负向水平位移略有增大。图5(b)对比了n值变化对最大剪应变的影响,发现同一深度处,随n值增大土体剪应变逐渐增大,但与试验值均较为接近。

图5(c)表明控制频率比n越大放大效应越明显。控制频率比n取3、5和7对应的地表峰值加速度放大倍数分别为1.09、1.18和1.29。表明控制比n越大,且在实际计算中低估土体阻尼的频率范围越大,则地震波所含能量较高的频率落在这部分的范围也越大,地震波能量衰减相对较慢,地震响应较强。

图5(d)中,同样由于控制频率比在实际计算中对于阻尼的影响作用,n值取3、5和7,阿里亚斯强度最终值分别为7.68、7.14和6.61 m/s,呈逐渐减小趋势。图5(e)中,地表加速度反应谱在0.2～0.5 s内,随n值增大放大效应越来越明显。

图5综合表明,与离心机试验实测值相比,阻尼比ξ=4%条件下,控制频率比n取5时模拟结果相对较为精确,且与阻尼比影响程度相比控制频率比的影响相对较小。

4.3 强地震动下的计算结果分析

图6表示在Kobe波作用下,阻尼比ξ取4%、控制频率比值n取5时,土层各计算结果对比。

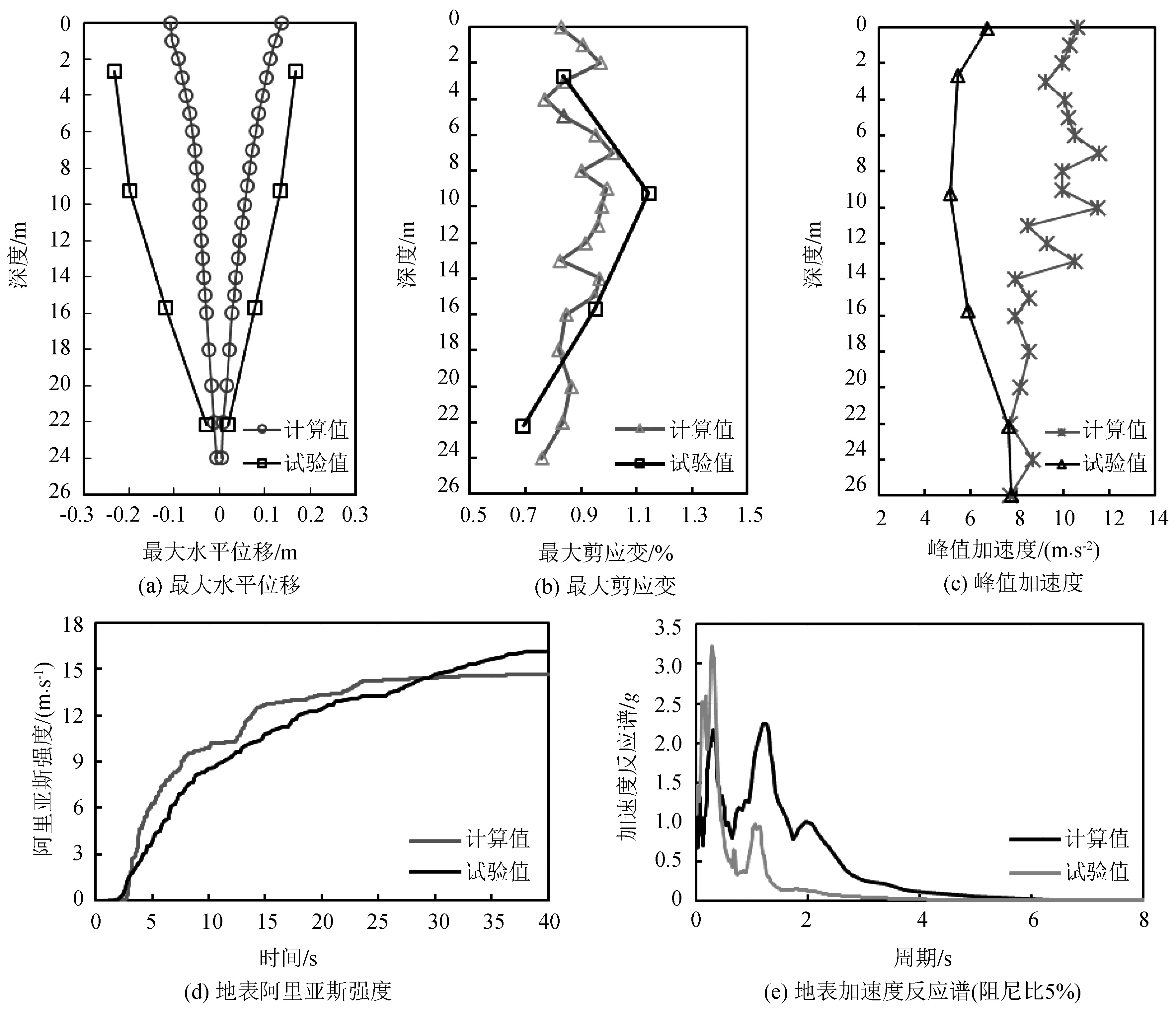
图6 计算值与试验值对比(ξ=4%,n=5,Kobe波)Fig.6 Comparison between calculated and experimental values (ξ=4%,n=5,Kobe)

图6(a)中,与小震Loma Prieta波作用下相比,土层侧向最大位移试验值与计算值的差距增大。正向最大水平位移计算值比离心机实测值略大,而负向最大水平位移在接近地表处,试验值约为计算值的2倍。地表正负向最大位移计算值分别达到13.8 cm和10.9 cm。

图6(b)显示土层各深度处最大剪应变值均在0.8%左右,最大1.02%,最小0.76%。同图5(b)对比,表明土层在强震作用下剪应变急剧增大,数值模拟结果与试验值相比精确性降低。同Loma Prieta波相比,由于Kobe波强度较大,土层剪应变平均增大8倍左右,而二者的峰值加速度比值仅为2.3,这也从侧面反映了土体非线性对地震响应的影响。

图6(c)表明干砂土层在大震下峰值加速度计算值随深度减小放大效应并不明显。与输入地震动峰值加速度0.76g相比,地表峰值加速度试验实测值略有减小,计算值的放大倍数仅为1.38。

图6(d)中,阿里亚斯强度时程曲线试验实测值与计算值变化趋势大致相同,且最终阿里亚斯强度值分别为16.1 m/s和14.6 m/s,相差11.2%。图6(e)中,地表加速度反应谱试验值与计算值均在0.2～0.5 s和1.0～1.5 s有明显放大效应,但不同的是在0.2～0.5 s内计算值大于试验值,而在1.0～1.5 s内试验值大于计算值。

综合分析图6,阻尼比ξ=4%、控制频率比n=5条件下,以Kobe波的离心机试验实测值为基准,同Loma Prieta波相比,该波作用下土层水平位移和地震加速度反应数值模拟结果精确度降低。

5 结论

利用OpenSees开源有限元计算程序,对比离心机试验,建立相应的原型场地剪切梁模型;考虑土层剪切波速与模量衰减关系,对不同地震荷载作用下工况进行数值模拟,分析采用瑞利阻尼方法进行场地动力计算时,不同阻尼比和控制频率比对场地加速度和侧向变形计算的影响。主要结论如下:

(1) 场地非线性地震响应域分析计算采用瑞利阻尼方法时,阻尼比和控制频率比不同取值对场地加速度和侧向变形计算结果的影响不可忽视。

(2) 对比离心机试验,对Loma Prieta波作用下的计算结果进行综合分析,确定Nevada干砂阻尼比取4%、控制频率比n为5时,地震响应数值模拟结果相对较为精确。

(3) 对于不同地震动Loma Prieta波和Kobe波输入条件下的计算结果对比表明,对于确定的瑞利阻尼系数,小震作用下土体应变较小,数值模拟结果相对较为精确,而强震作用下土体应变较大,数值模拟结果精确度降低,与地震波强度影响有关。

(4) 本文确定的Nevada干砂阻尼比4%要高于Phillips C等[10]建议的饱和内华达砂阻尼比3%。李文泱等[11]研究表明由于动力作用下饱和砂的阻尼比随孔压增长而降低,故干砂阻尼应高于饱和砂阻尼。在进行具体场地地震响应评价时,要综合考虑场地自振频率、土体饱和度和地震波特性来确定阻尼比和控制频率。

References)

[1] Idriss I M,Sun J.User’s Manual for SHAKE91-A Computer Program for Conducting Equivalent Linear Seismic Response Analyses of Horizontally Layered Soil Deposits:Center for Geotechnical Modeling[R].California:Department of Civil & Environmental Engineering,University of California,Davis,1992.

[2] 吴世明.土动力学[M].北京:中国建筑工业出版社,2000. WU Shi-ming.Soil Dynamics[M].Beijing:China Architecture & Building Press,2000.(in Chinese)

[3] 栾茂田,邵宇.土体地震反应非线性分析方法比较研究[C]//第五届全国土动力学学术会议论文集,1998:203-209. LUAN Mao-tian,SHAO Yu.Comparison Research of Nonlinear Analysis Method of Seismic Response of Soil[C]//Proceedings of the 5thNational Conference on Soil Dynamics,1998:203-209.(in Chinese)

[4] Hardin B O,Drnevich V P.Shear Modulus and Damping in Soils:Design Equations and Curves[J].Journal of Soil Mechanics and Foundation,ASCE,1972,98(SM7):603-642.

[5] Phillips C,Hashash Y M A.Damping Formulation for Nonlinear 1D Site Response Analyses[J].Soil Dynamics & Earthquake Engineering,2009,29(7):1143-1158.

[6] Hudson M,Idriss I M,Beikae M.User Manual for QUAD4m:A Computer Program to Evaluate the Seismic Response of Soil Structures Using Finite Element Procedures and Incorporating a Compliant Base[D]:Berkeley:University of California,1994.

[8] Hashash Y M A,Dashti S,Romero M I,et al.Evaluation of 1-D Seismic Site Response Modeling of Sand Using Centrifuge Experiments[J].Soil Dynamics & Earthquake Engineering,2015,78:19-31.

[9] Mazzoni S,Mckenna F,Scott M H,et al.The Open System for Earthquake Engineering Simulation (OpenSEES) User Command-Language Manual[M].California:University of California,2006.

[10] Phillips C,Hashash Y M A,Olson S M,et al.Significance of Small Strain Damping and Dilation Parameters in Numerical Modeling of Free-field Lateral Spreading Centrifuge Tests[J].Soil Dynamics & Earthquake Engineering,2012,42:161-176.

[11] 李文泱,刘惠珊.孔隙水压力对饱和砂的剪切模量和阻尼比的影响[J].岩土工程报,1983(4):56-67. LI Wen-yang,LIU Hui-shan.Influence of Pore Water Pressure on Shear Modulus and Damping Ratio of Saturated Sands[J].Chinese Journal of Geotechnical Engineering,1983(4):56-67.(in Chinese)

Influence of Rayleigh Damping on Nonlinear Seismic Responses of Sand Sites

WANG Hao1,2, GAO Guang-yun1,2, YANG Cheng-bin3

(1.DepartmentofGeotechnicalEngineering,TongjiUniversity,Shanghai200092,China; 2.KeyLaboratoryofGeotechnicalandUndergroundEngineeringofMinistryofEducation,TongjiUniversity,Shanghai200092,China; 3.SchoolofResourcesandEnvironmentalEngineering,HefeiUniversityofTechnology,Hefei230009,Anhui,China)

Under seismic loads, some phenomena will occur in free field, including lateral deformation of soil and ground response amplification. When evaluating the seismic response of free field, it is the highly nonlinear characteristics of soil that significantly influences the results obtained when utilizing differing damping ratio and shear modulus values and is one of the reasons that experimental results and calculated results can largely differ. Currently, the Rayleigh damping method is most commonly used for site seismic dynamic response analysis. Based on a simplified version of this method, this study analyzes the influence of different values of soil damping ratio and control frequency on calculated results. Using the finite element platform OpenSees, we have adopted the PDMY constitutive model fitted for soil dynamic analysis and established a one-dimensional shear beam model to simulate the three-dimensional free field. Compared with centrifuge model test results, this study analyzed the effects of the Rayleigh damping on the site response and lateral deformation of free field. In the case of Nevada dry sand (relative density 60%), there is good agreement between the calculated results and the test results when the damping ratio and control frequency ratio are set as 4% and 5%, respectively. Our comprehensive analysis suggests that special attention should be paid to value selection of Rayleigh damping in the time domain calculations of site nonlinear response.

seismic response; lateral deformation; damping ratio; Rayleigh damping coefficient; centrifuge test; OpenSees

2016-04-25 基金项目:国家自然科学基金项目(41372271) 作者简介:王 豪(1990-)，男，硕士,主要从事土动力学和地震工程的研究。E-mail:1431939@tongji.edu.cn。

TU47

A

1000-0844(2016)06-0909-07

10.3969/j.issn.1000-0844.2016.06.0909