地铁列车荷载作用下黏弹性地基动应力特征分析

丁 智, 李丹薇, 谢宗星, 魏新江

(1.浙江大学城市学院土木工程系,浙江 杭州 310015; 2.浙江大学海洋学院,浙江 舟山 316021)

地铁列车荷载作用下黏弹性地基动应力特征分析

丁 智1, 李丹薇1, 谢宗星2, 魏新江1

(1.浙江大学城市学院土木工程系,浙江 杭州 310015; 2.浙江大学海洋学院,浙江 舟山 316021)

基于Kelvin空间半无限体黏弹性解,以单个轮轴荷载为例,研究地铁列车荷载下地基土动应力状态、应力路径及主应力轴旋转等应力变化规律,并与相应弹性解下的各动应力特征进行对比分析,探讨更适用于工程实际的地基附加动应力特征解。结果表明:弹性地基与黏弹性地基中的各应力状态变化总体趋势、主应力轴旋转变化趋势相同,但极限应力状态各应力分量大小及应力路径形状有明显差别,考虑黏弹性解更符合软土区地铁长期变形实际工况;并对单轮荷载下动应力特征的黏弹性解进行参数分析,发现特征系数对应力分量影响具有不同特性。

地铁; 黏弹性地基; 应力状态; 应力路径; 主应力轴旋转

0 引言

随着地下空间建设的迅猛发展,城市交通的枢纽任务正逐渐由地上交通转由地铁轨道交通承担,然而地铁运营带来的系列问题却不容小觑。如上海地铁一号线在建成后未通车期间基本未发生沉降,但运营仅8个月后沉降增加了30～60 mm,通车4年内部分路段沉降超过140 mm[1];南京地铁一号线西延线在运营4年后隧道最大累计沉降达122 mm[2],均远远超过了标准的20 mm总沉降量。许多原因可引发地铁隧道沉降,如土体的固结、蠕变或列车长期荷载作用下的振陷以及地下水位的变化等。其中由于地铁列车移动荷载引发振动响应,从而使土体单元发生应力变化,是导致沉降的一个重要因素[3],尤其在隧道运营初期,由于列车行车密度、线路通过的荷载增加,隧道沉降呈迅速增加趋势[4]。

目前针对半无限体弹性地基的研究已较为成熟,如张昀青[5]以Duhamel积分为基础,采用 Fourier变换和Floquet变换等方法,对移动荷载作用下半无限体中任一点的动力响应进行了研究;蒋建群等[6]研究了弹性半空间体在移动集中荷载作用下的稳态响应;笔者在文献[3]中,将地铁列车移动荷载简化为多个移动轮轴荷载,基于弹性半空间内Mindlin解研究了地铁列车荷载作用下地基土中的动应力特征。以Mindlin解为基础导出的地基变形计算公式与实测值相对吻合较好,但Mindlin计算理论并未考虑土体的黏弹性特征,与工程实际情况仍有一定差距。魏星等[7]将单个轮轴荷载叠加为多轮组车辆荷载研究了公路地基的附加动应力问题,但并未考虑动应力特征参数变化对地基附加动应力的影响变化。

软土区土体具有明显的黏弹性性质,即在荷载的作用下土体变形与时间有着密切的关系。已有学者开始采用黏弹性模型对半无限体地基进行研究,如祝彦知[8]假定半无限体为线性黏弹性介质,根据准静态黏弹性-弹性对应原理,推导Kelvin半无限黏弹性体内部受集中力作用下的应力、位移解;戚桂峰等[9]采用格林函数法推导出的解析解研究了黏弹性半空间体自由场地在移动简谐荷载作用下的振动规律;李皓玉等[10]以Burgers模型模拟沥青面层,将路面简化为半空间地基上的层状黏弹性体系,计算分析了车辆移动荷载下层状黏弹性体系的振动特性。但关于地铁列车荷载下黏弹性地基的动应力特征还未见报道。

研究表明,当荷载速度与地基土剪切波速比值小于0.4时,土单元应力的静力解大小接近动力解,为便于工程应用可用前者代替后者[11]。目前我国地铁列车运营情况符合静力解适用条件,故本文采用静力方法计算。文中首先基于Kelvin空间半无限体黏弹性解[8],将列车移动荷载简化为单个轮轴荷载;然后以荷载与考察点间的水平距离变化模拟荷载移动情况,研究地铁运营引起的黏弹性均质地基中的动应力状态、应力路径变化及主应力轴旋转;最后计算分析得出地铁列车荷载作用线正下方的地基土单元动应力特征,并与相应弹性解下的各动应力特征进行对比分析,探讨更适用于工程实际的地基附加动应力特征解。

1 竖向力下半空间黏弹性体的应力解

由文献[8],做出如下假定:地基土为空间半无限体,且是均匀各向同性、连续一致的线性黏弹性介质;土体在外部集中力作用下呈三维复杂应力状态,且应力球张量和应变球张量之间符合弹性关系;应力偏张量和应变偏张量之间符合Kelvin黏弹性本构方程。建立如图1所示模型。

图1 内部竖向集中力作用下的半无限体模型Fig.1 Semi-infinite model subjected to a vertical concentrated load

(1)

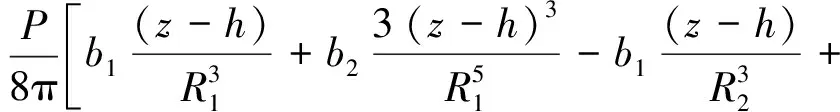
(2)

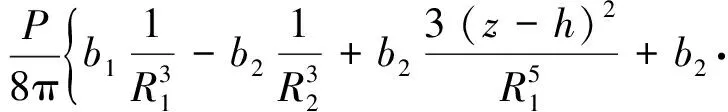
(3)

r为集中力作用线到计算点的水平距离,

b1=(1-2μ)/(1-μ), b2=1/(1-μ),

b3=(3-4μ)/(1-μ), b4=μ(1-2μ)/(1-μ),

b5=μ/(1-μ), b6=1-2μ。

(4)

其中:μ为土的泊松比(取0.45)。

(5)

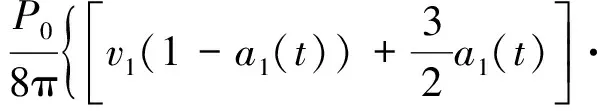
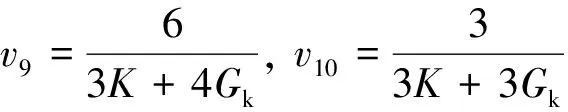
式中:K为体积弹性模量(下文2节分析中取20 MPa);Gk为剪切模量(取3 MPa);ηk为黏滞系数(取0.2 GPa·d)。

2 地铁运营引起的土体应力状态变化

如图2所示,本文将地铁荷载简化为单个轮轴荷载。地铁列车荷载作用深度为z=10 m,计算土单元位于隧道正下方3 m(x=0,y=0 m,z=13 m),地铁列车以v0=22.2 m/s(80 km/h)的速度运行,以计算土单元与单轮荷载水平距离变化模拟地铁运行时荷载的移动,分析均质地基中的动应力状态变化。

图2 单个轮载移动引起的土单元应力状态分析示意图Fig.2 Diagram of stress state of soil element induced by moving single wheel

列车与计算土单元的水平距离为x=-30 m(t=0)时开始计算土单元的应力状态变化,直到列车离开计算土单元水平距离x=30 m(t=2.7 s)。位于地铁列车移动荷载作用线正下方(即y=0平面)的土单元,其剪应力τxy、τyz均为0,故沿y轴方向,即垂直列车运行方向上的动应力即为主应力σy。由于σy值很小且始终为中主应力σ2,可忽略其影响,现仅对x-z平面上的应力状态和主应力轴变化进行研究计算。

由图3发现,黏弹性地基中的正应力σx与σz随荷载移动变化的特征图像关于x=0对称,且剪应力τxz的图形关于x=0反对称。当荷载移动接近计算土单元正上方时,土单元应力变化较大,伴有峰值出现;而随着荷载远离计算土单元,三个应力分量大小逐渐接近并趋向于零。

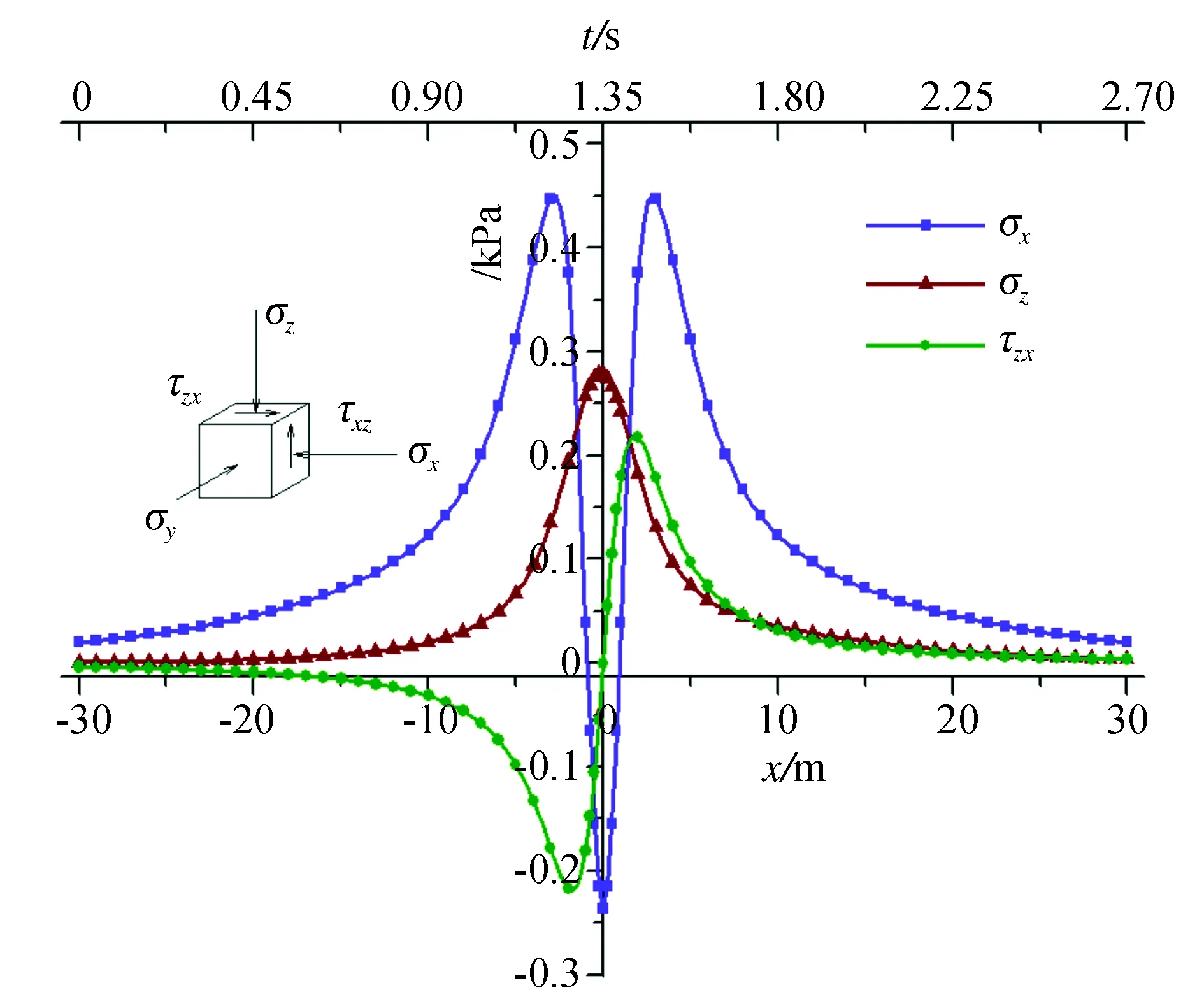
图3 计算土单元动应力随时间和荷载的变化Fig.3 Change of dynamic stress of soil element with time and loading

图4给出了地铁列车荷载作用线正下方地基土中各动应力弹性解与黏弹性解的变化特征,对比分析规律如下:

(1) 各应力分量的弹性解与黏弹性解随时间和荷载的变化趋势大体一致。弹性地基与黏弹性地基中正应力σx与σy随列车荷载移动变化均关于x=0对称,剪应力τyz关于x=0反对称。当列车荷载逐渐远离观察点时,弹性解与黏弹性解逐渐接近,剪应力、切应力都趋向于零。

(2) 随着荷载向观察点移动,弹性地基与黏弹性地基中各应力均有峰值出现,且峰值点位置接近,与地基的弹性或黏弹性无关:σx1、σx2峰值点均为x=±a,x=0,见图4(a);σz1、σz2峰值点均为x=0,见图4(b);τzx1、τzx2峰值点均为x=0。故列车移动荷载作用下,考虑弹性地基与黏弹性地基中各应力极限出现位置时,为提高计算分析效率,弹性解可以适用。

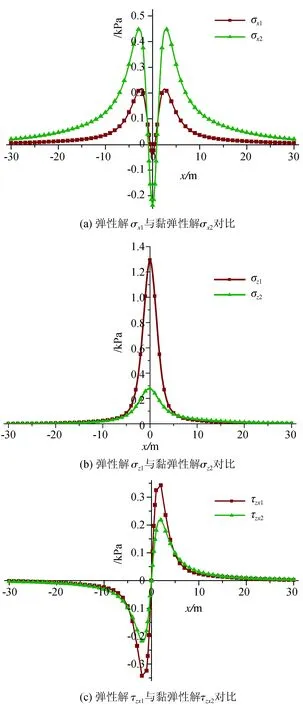
图4 各应力分量弹性解与黏弹性解对比图Fig.4 Comparison between elastic solution and viscoelastic solution of each stress component

(3) 如图4(a),当列车荷载运行到应力极限应力位置(x=±a)时,σx1<2σx2。因此考虑列车运行方向上的应力时,采用弹性地基模型计算较为危险,黏弹性模型更优。

(4) 如图4(b)、(c),当列车荷载运行到应力极限应力位置(x=0)时,σz1远大于σz2,故考虑列车运行中地基竖向附加应力变化趋势时,采用黏弹性地基模型计算更为合理。同理,如图4(c),τzx1>τzx2,考虑列车运行中地层水平面上的剪应力影响较小时,在工程实际中利用黏弹性解计算τzx更为合理。

3 土单元的应力路径和主应力轴旋转

3.1 应力路径的特征分析

已有学者[7]就弹性解下公路交通荷载移动速度对地基动应力路径的影响进行过研究。图5给出了弹性解下速度对应力路径的影响情况。在速度较低时,浅层地基与深层地基中的应力路径横、纵轴随速度均缓慢增加。但速度较大时,浅层地基中的应力路径会出现不规则角点,且纵轴加速增大,横轴显著减小;深层地基中的应力路径与浅层地基变化规律有所不同,横、纵轴均显著增大。因此在地基动应力特征模拟及沉降计算中,应考虑荷载移动速度对应力路径的影响。

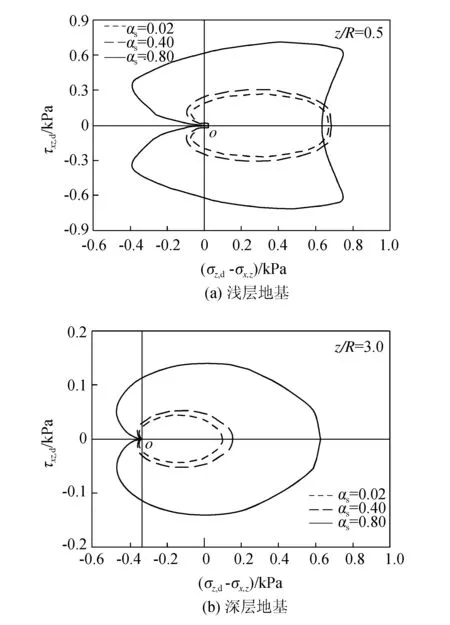
图5 弹性解下速度对应力路径影响Fig.5 Effect of moving speed on stress paths under elastic solution

我国地铁列车最高运行速度约为80 km/h,地基剪切波速约为260 km/h,二者比值αs=0.308,小于0.4,属于低速运行状态,因此文献[7]中荷载高速移动条件在地铁实际运行中并不存在。地铁列车运行时,速度对弹性地基应力路径变化影响甚微,可予以忽略。由本文第2节可知,弹性解与黏弹性解随时间和荷载的变化趋势大致一致,因此在黏弹性地基中,地铁运行速度对地基动应力路径变化仍可忽略,本文不予讨论。

移动荷载作用下,黏弹性地基与弹性地基中的土单元动应力路径区别较大。如图6,α为最大主应力σ1与x轴的夹角,从x轴到主应力轴方向旋转,顺时针为正,逆时针为负,其范围是-π/2～π/2。

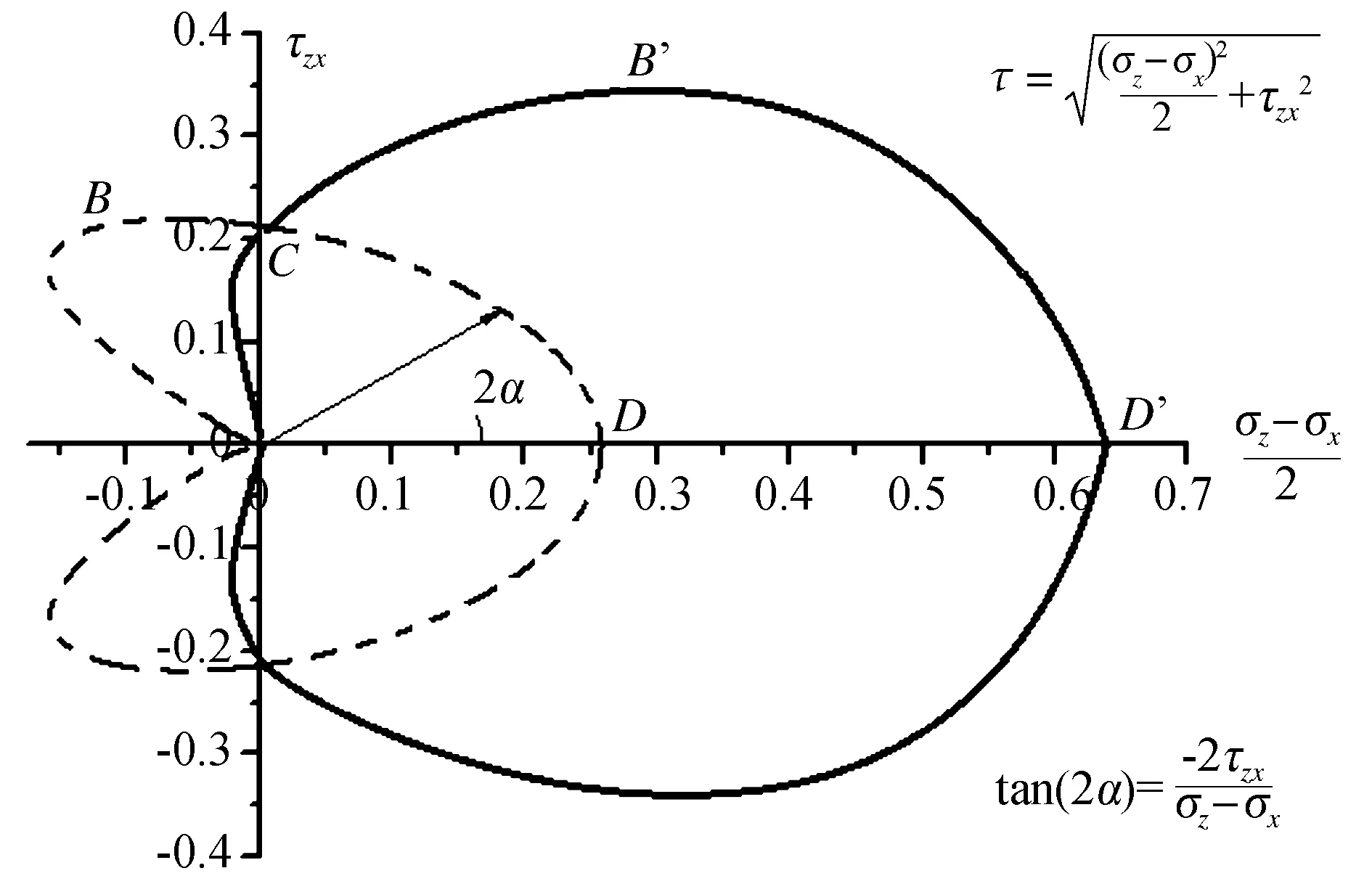
图6 弹性解与黏弹性解下的应力路径对比图(αs=0.30,虚线、实线分别表示黏弹性解、弹性解)Fig.6 Comparison of stress paths under elastic and viscoelastic solutions (αs=0.30,dotted and solid lines respectively indicate the viscoelastic solution and elastic solution)

随着荷载向土单元移动,黏弹性解下的应力分量差增长速度大于水平剪应力的增长速度,而弹性解下的情况则正好相反。到达C点时,两种解下的应力差分量均为0,即土单元处于纯剪状态时,黏弹性解与弹性解下的τzx值相等。但黏弹性解下的剪应力最大值B点在C点前出现,弹性解下的剪应力最大值B’在C点后出现,且B点τzx值明显小于B’点。剪应力最大值出现后,两种解下的τzx均开始减小,σz-σx继续增大,黏弹性与弹性解的应力分量差最大值分别出现在D、D’点,且后者值大于前者的2倍,此时,荷载运动到土单元的正上方,水平剪应力为0,土单元处于三轴纯剪切状态。荷载远离土单元的过程中,动应力状态与上述过程相反。

3.2 主应力轴旋转的特征分析

图7反映了最大主应力σ1与x轴的夹角α随轮载移动和时间的变化关系。黏弹性与弹性解下的主应力轴旋转变化规律趋势相同:轮载由远处移动到土单元正上方过程中,α逐渐增大至π/2;此后轮载远离土单元,α突变为-π/2,并逐渐减小。上述过程中主应力轴顺时针旋转了180°。

列车远离土单元时,弹性解与黏弹性解下的主应力轴旋转均较为缓慢;列车越靠近土单元(x<5 m)主应力轴旋转越快,且黏弹性解下的旋转速度约为弹性解的2倍。整个过程中,黏弹性解的α值均明显大于弹性解。因此以弹性解最大主应力σ1与x轴夹角的误差较大,尤其是轮载靠近计算土单元时误差更为明显。

图7 弹性解与黏弹性解下的主应力轴旋转对比图(绿色、红色分别表示黏弹性解、弹性解)Fig.7 Comparison of principal stress axes rotation under elastic and viscoelastic solutions (Green and red respectively indicate the viscoelastic solution and elastic solution)

4 黏弹性解下的动应力特征参数分析

图8给出了黏弹性地基中不同体积弹性模量K下的σx和σz随荷载移动的变化过程。分析发现:如图8(a),相同条件下,σx的值随K值单调递增,且在K值较小时增幅明显;如图8(b),在-5～5 m范围内,σz的值随K值单调递增,轮载移动超出此范围时,σz的值随K值增大递减。当荷载在远处(|x|>30 m)时,K对σx和σz的影响较小,可忽略不计。

图9给出了黏弹性地基中不同剪切弹性模量Gk下的σx随荷载移动的变化过程。在轮载移动至计算土单元过程中,σx随Gk增大呈递增趋势;当荷载位于近距离(|x|<3 m)或远处(|x|>30 m)时,σx值随Gk的变化甚微,可忽略。进一步分析发现,剪切模量Gk对σx、σz的影响相对体积模量K更显著;而体积模量K对τxz,剪切模量Gk对τxz、σz,黏滞系数ηk对τxz、σz、σx均无明显的影响。

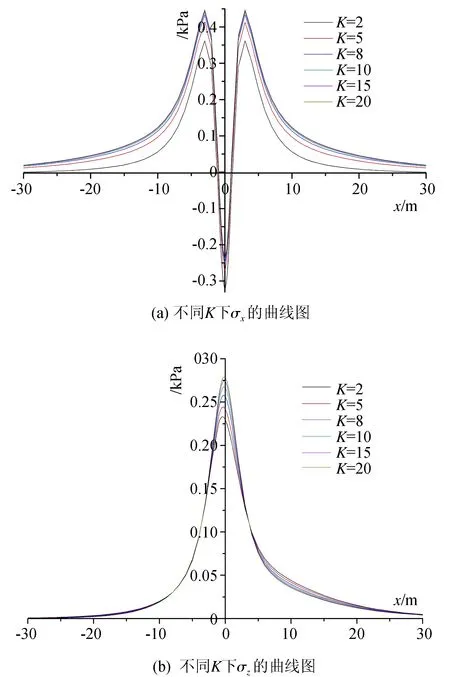
图8 不同体积模量K下土单元应力状态Fig.8 Stress state of soil element under different bulk modulus K

图9 不同剪切模量Gk下σx的变化Fig.9 Change of σx under different shear modulus Gk

5 结 语

本文基于Kelvin空间半无限体黏弹性解,以单个轮轴荷载为例,对地铁列车运营引起的地基动应力状态变化进行分析,得出黏弹性地基中列车移动荷载作用下土单元应力和主应力轴旋转变化规律,同时与弹性解下的荷载动应力变化规律进行对比分析,得到以下结论:

(1) 单个轮轴荷载作用下,弹性地基与黏弹性地基中各应力变化总体趋势相同,且峰值出现位置几乎与地基土体弹性或黏弹性无关,但在各应力分量的大小上黏弹性解与弹性解有明显区别。

(2) 研究地铁列车荷载作用下地基动应力峰值出现点位时,为提高计算分析效率,弹性解可以适用;而研究地基动应力影响时,采用弹性解计算列车运行方向上的应力σx较为危险,黏弹性解更符合安全性;采用弹性解计算所得的地基竖向附加应力σz、地层水平剪应力τyz偏安全,利用黏弹性解计算更符合应力变化趋势。

(3) 黏弹性地基中应力路径大小、形状都与弹性解下有明显差别;两种地基中主应力轴旋转变化的趋势基本相同,但黏弹性解的最大主应力σ1与x轴的夹角α值明显大于弹性解,且随着荷载与土单元距离减小,二者差值增大。故考虑地基土的黏弹性有利于减小动应力计算误差。

(4) 对单轮荷载下动应力特征的黏弹性解进行参数分析,发现不同系数下的应力分量变化有所不同:剪切模量Gk对σx、σz的影响相对体积模量K更显著;而体积模量K对τxz,剪切模量Gk对τxz、σz,黏滞系数ηk对τxz、σz、σx则均无明显的影响。

References)

[1] 张冬梅,李钰.地铁荷载引起的盾构隧道及土层长期沉降研究[J].防灾减灾工程学报,2015,35(5):563-567. ZHANG Dong-mei,LI Yu.Long-term Settlement of Shield Tunnel in Soft Clay due to Vehicle Vibration[J].Journal of Disaster Prevention and Mitigation Engineering,2015,35(5):563-567.(in Chinese)

[2] 狄宏规,周顺华,宫全美,等.软土地区地铁隧道不均匀沉降特征及分区控制[J].岩土工程学报,2015,37(增刊2):74-79. DI Hong-gui,ZHOU Shun-hua,GONG Quan-mei,et al.Different Settlement of Metro Tunnels and Its Zonal Controlin Soft Deposits[J].Chinese Journal of Geotechnical Engineering,2015,37(Supp2):74-79.(in Chinese)

[3] 丁智,葛国宝,魏新江,等.地铁列车运营引起的地基土应力状态变化分析[J].岩土工程学报,2013,35(增刊2):647-651. DING Zhi,GE Guo-bao,WEI Xin-jiang,et al.Variation of Stress State of Foundation Soils Included by Running Subway[J].Chinese Journal of Geotechnical Engineering,2013,35(Supp2):647-651.(in Chinese)

[4] 王如路.上海软土地铁隧道变形影响因素及变形特征分析[J].地下工程与隧道,2009,1(1):1-6. WANG Ru-lu.Factors Influencing Deformation of Shanghai Soft Soil Metro Tunnel and Deformation Analysis[J].Underground Engineering and Tunnels,2009,1(1):1-6.(in Chinese)

[5] 张昀青.移动荷载作用下半无限体的动力响应解[J].岩土力学,2004,25(6):955-957. ZHANG Yun-qing.Dynamic Response of Semi-infinite Body under Moving Loads[J].Rock and Soil Mechanics,2004,25(6):955-957.(in Chinese)

[6] 蒋建群,周华飞,张土乔.弹性半空间体在移动集中荷载作用下的稳态响应[J].岩土工程学报,2004,26(4):440-444. JIANG Jian-qun,ZHOU Hua-fei,ZHANG Tu-qiao.Steady-state Response of an Elastic Half-space under a Moving Point Load[J].Chinese Journal of Geotechnical Engineering,2004,26(4):440-444.(in Chinese)

[7] 魏星,王刚.多轮组车辆荷载下公路地基的附加动应力[J].岩土工程学报,2015,37(10):1924-1930. WEI Xing,WANG Gang.Induced Dynamic Stresses in Subsoil of Road Subjected to Moving Vehicle Load with Wheel Groups[J].Chinese Journal of Geotechnical Engineering,2015,37(10):1924-1930.(in Chinese)

[8] 祝彦知.Kelvin半无限体内部受集中力作用时的黏弹性解[J].工业建筑,2005,35(12):55-60. ZHU Yan-zhi.Analytical Solutions of Kelvin’s Viscoelastic Half-infinite Space Subject to Interior Vertical Center Loading[J].Industrial Construction,2005,35(12):55-60.(in Chinese)

[9] 戚桂峰,陈士海,张子华,等.移动集中简谐荷载下黏弹性自由场地振动规律研究[J].山东科技大学学报:自然科学版,2012,31(1):57-61. QI Gui-feng,CHEN Shi-hai,ZHANG Zi-hua,et al.Study on Vibration of Visco-elastic Free Field under Moving Concentrated Harmonic Load[J].Journal of Shandong University of Science and Technology:Natural Science,2012,31(1):57-61.(in Chinese)

[10] 李皓玉,杨绍普,刘进,等.移动分布荷载下层状黏弹性体系的动力响应分析[J].工程力学,2015,32(1):120-127. LI Hao-yu,YANG Shao-pu,LIU Jin,et al.Dynamic Response in Multilayered Viscoelastic Medium Generated by Moving Distributed Loads[J].Engineering Mechanics,2015,32(1):120-127.(in Chinese)

[11] 王常晶,陈云敏.移动荷载引起的地基应力状态变化及主应力轴旋转[J].岩石力学与工程学报,2007,26(8):1698-1704. WANG Chang-jing,CHEN Yun-min.Stress State Variation and Principal Stress Axes Rotationog Ground Induced by Moving Loads[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(8):1698-1740.(in Chinese)

Dynamic Stress Characteristics of Viscoelastic Foundations under Subway Train Loads

DING Zhi1, LI Dan-wei1, XIE Zong-xing2, WEI Xin-jiang1

(1.DepartmentofCivilEngineering,ZhejiangUniversityCityCollege,Hangzhou310015,Zhejiang,China; 2.OceanCollege,ZhejiangUniversity,Zhoushan316021,Zhejiang,China)

This paper presents a comparative evaluation of elastic and viscoelastic solutions to identify more suitable and practical engineering solutions. Based on the viscoelastic solutions of a Kelvin's space half-infinite body, as an example, we analyzed the dynamic stress response under moving subway loads to illustrate the characteristics of dynamic stress, the stress path, and the principal stress axis rotations. By applying two solutions, we found the numerical results for the development trends of the dynamic stress state and principal stress axis rotation to be similar. We also found discrepancies in the dynamic stress of the ultimate state and stress path. Additionally, our results indicate that a viscoelastic solution is more applicable to actual working cases of long-term metro tunnel deformation in soft soil areas. Moreover, according to our analysis of viscoelastic solutions of dynamic stress characteristics under single-wheel loads, we found different feature coefficients to have different influences on stress characteristics.

subway; viscoelastic foundation; stress state; stress path; principal stress axes rotation

2016-01-20 基金项目:浙江省自然基金项目(LQ16E080008) ；国家自然科学基金项目(51278463,51508506) 作者简介:丁 智(1983-)，男，安徽铜陵人，博士，副教授，主要从事轨道施工及运营对周边环境影响的研究与教学工作。 E-mail: dingz@zucc.edu.cn。

TU443

A

1000-0844(2016)06-0889-07

10.3969/j.issn.1000-0844.2016.06.0889