危岩体在地震作用过程中的失稳模式及稳定性评价
2017-01-13彭宁波王逢睿夏江涛
彭宁波, 孙 博, 王逢睿, 3, 夏江涛
(1.淮阴工学院 建筑工程学院,江苏 淮安 223021; 2.中铁西北科学研究院有限公司,甘肃 兰州 730000;3.兰州大学 土木工程与力学学院,西部灾害与环境力学教育部重点实验室,甘肃 兰州 730000)
危岩体在地震作用过程中的失稳模式及稳定性评价
彭宁波1, 孙 博2, 王逢睿2, 3, 夏江涛1
(1.淮阴工学院 建筑工程学院,江苏 淮安 223021; 2.中铁西北科学研究院有限公司,甘肃 兰州 730000;3.兰州大学 土木工程与力学学院,西部灾害与环境力学教育部重点实验室,甘肃 兰州 730000)
地震作用过程中地震加速度通常呈先增大后减小的特征。利用拟静力法对危岩的稳定性进行分析时,考虑地震过程中地震加速度的变化,对山西太原天龙山危岩体加固工程中的同一危岩体分别以滑塌式和倾倒式破坏模式进行计算,发现地震作用过程中危岩体可能在两种破坏失稳模式之间相互转化。将此问题扩展至一般情况进行计算并讨论,得出如下结论:地震力对危岩体破坏作用的贡献大小不同,通常情况下,地震作用力对危岩的倾覆力矩贡献相对较大;进行稳定性评价时应考虑地震作用过程,以安全系数最先达到1.0的破坏模式作为危岩体的可能破坏模式进行计算;对危岩体进行抗震加固设计时应对加固设计进行多种工况下的校核,保证其在地震作用过程中不同危险状态的稳定性。
拟静力法; 地震作用过程; 危岩体; 破坏模式; 稳定性
0 引言
拟静力法是使用最早、最广泛的对边坡进行动力稳定性计算的方法。它将地震力的瞬时作用等效为水平方向和竖直方向的加速度施加在岩体结构上,然后基于极限平衡理论进行计算,通过求解潜在不稳定滑体的静力平衡方程或力矩平衡方程,来确定潜在滑体的安全系数[1]。
拟静力法虽然具有一定的缺陷,但由于其物理意义明确、计算简便,现仍是工程中的主要计算方法。多年来,很多学者致力于这一方法的改进和发展,以往的工作通常关注算法本身的改进以及潜在破坏面的确定和地震系数的选取[2-9]。地震系数确定以后,通过该地震系数对危岩体的安全系数进行计算,当破坏模式不确定时,通常对可能的几种模式都进行计算,然后选择安全系数较小的破坏模式作为危岩体的破坏模式。而地震作用是一个过程,通常地震波对危岩体的作用总是由小变大的,这一过程中危岩体的破坏模式可能会有所改变。不同的破坏模式选取不同的计算公式来评价危岩体的稳定性、确定危岩体锚固所需的锚固力,而由单一地震系数计算的锚固力不一定能满足地震过程中出现的其他危险状态,会导致工程计算出现严重的偏差。
本文将采用拟静力法分析危岩体的地震稳定性,讨论地震系数对危岩体破坏模式的影响,分析地震过程中危岩体可能出现的危险状态,并对其稳定性进行评价,以保证危岩体在整个地震作用过程中的稳定性。
1 危岩体的稳定性计算方法
1.1 危岩体的破坏模式
根据陈洪凯等[10]提出的危岩体破坏模式,将其分为3种:滑塌式破坏,倾倒式破坏和坠落式破坏(图1)。该分类方法中,岩体的力学机理清晰,几何形态明显,分类系统简明,在三峡库区危岩防治等工程中得到成功应用。
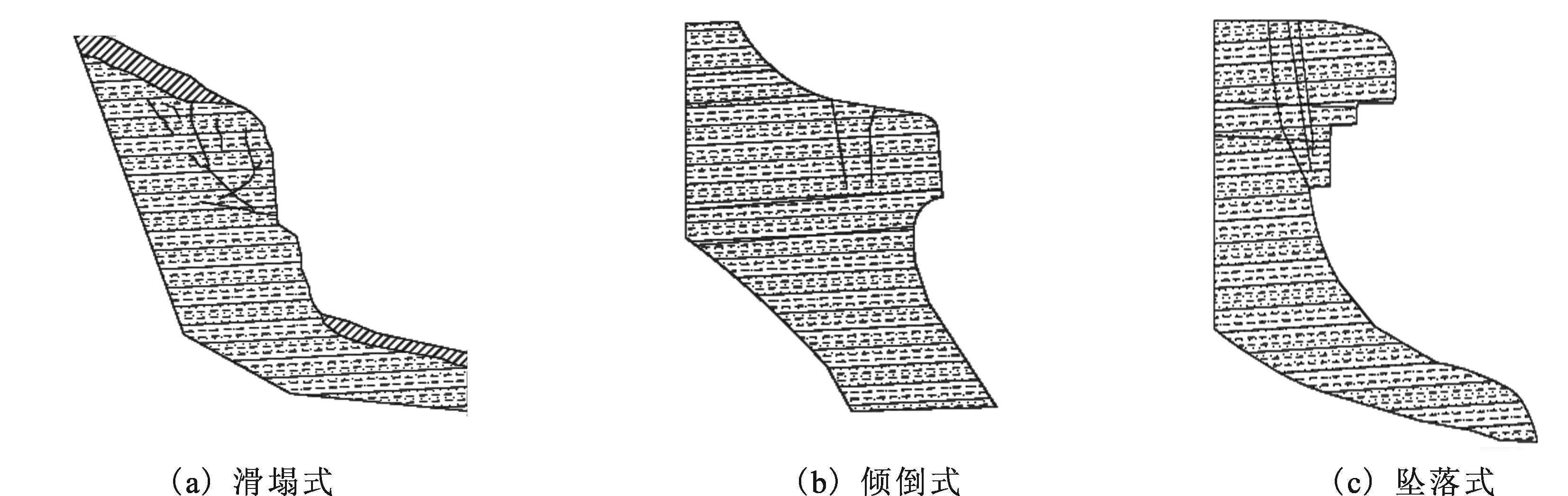
图1 危岩体的破坏模式[10]Fig.1 Failure mode of unstable rock[10]
1.2 稳定性计算[10]
对于静力作用下滑塌式破坏的危岩体来说,在地震作用下其破坏模式可能会由滑塌式转变成倾倒式破坏,故本文仅对这两种破坏模式的动力稳定性进行讨论。
(1) 后缘无陡倾裂隙的滑塌式破坏危岩(图2)
滑塌式破坏的稳定性系数是抗滑力与下滑力的比值,即
(1)
其中:W为危岩体自重;Q为地震力;V为裂隙水压力;c为后缘裂隙黏聚力标准值;β为滑面倾角;φ为后缘裂隙内摩擦角标准值;l为滑面总长度。
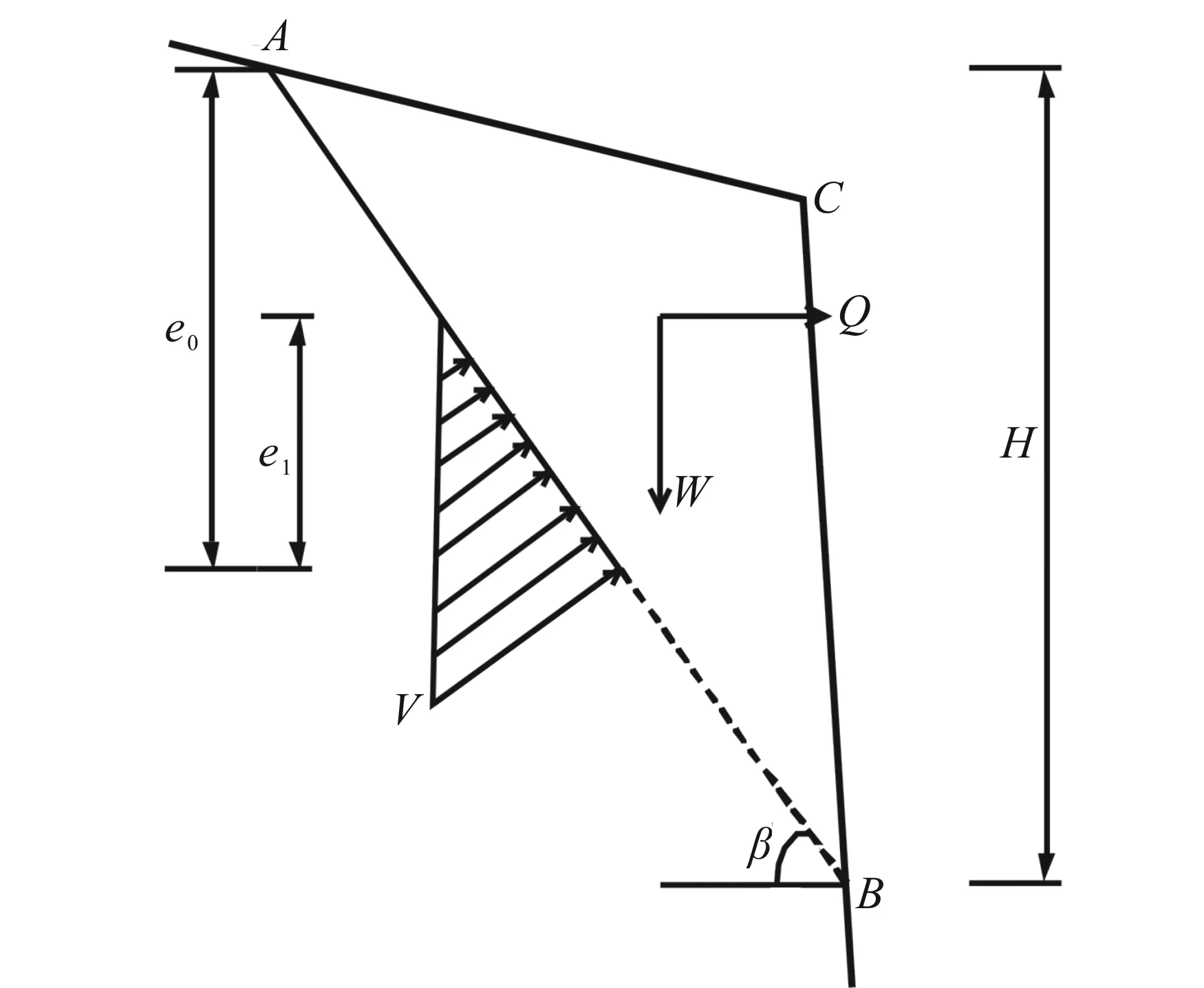
图2 滑塌式危岩(后缘无陡倾裂隙危岩)Fig.2 Sliding unstable rock
(2) 底部岩体抗拉强度控制的倾倒式破坏危岩(图3)

图3 倾倒式危岩(下部岩体抗拉强度控制)Fig.3 Toppling unstable rock
倾倒式破坏危岩体的稳定性系数是抗倾覆力矩与倾覆力矩的比值,即
(2)
其中:flk为岩体抗拉强度标准值;h为后缘裂隙深度;hw为裂隙充水高度;a为危岩体重心到倾覆点的水平距离,b为后缘裂隙未贯通段下端到倾覆点之间的水平距离;β为后缘裂隙倾角。
1.3 参数的选取
除地震系数之外,危岩结构面的抗剪强度c、φ值也是计算中的重要参数。文献[11]中利用危岩主控结构面抗剪强度参数贯通率法,通过实验研究危岩主控结构面的抗剪参数,认为主控结构面的抗剪强度参数与结构面的贯通率相关。
(3)
(4)

(5)
(6)
式中:R为贯通率,R=e0/H0。
危岩主控结构面抗剪强度参数贯通率法确定的c、φ值比使用长度加权法随机性要小,经现场观测验证计算结果比较符合实际情况。
1.4 破坏模式的判定
不同破坏形式危岩体的稳定性状态的判断根据如表1所列。

表 1 危岩体稳定状态[12]
当危岩体的稳定性系数F<1时,危岩体处于不稳定状态。对于同一个危岩体来说,采用不同破坏模式的公式计算所得到的稳定性系数是不同的,所以判断危岩体的破坏模式是确定稳定性的前提。
2 稳定性分析与讨论
2.1 算例
以山西太原天龙山石窟加固保护工程中的危岩体为例,计算简图见图4。其中,H=22.2m,e0=15.6m,a=2.8m,b=3.2m,h=8.9m,β=43°,完整岩石黏结力为400kPa,内摩擦角为25°,危岩体后缘结构面黏结力为70kPa,内摩擦角为25°,岩石抗压强度为20MPa,岩石抗拉强度标准值取360kPa,岩体重度取25.2kN/m3;W1=3 460kN,W2=2 880kN;裂隙水高度取后缘裂隙高度的1/3。
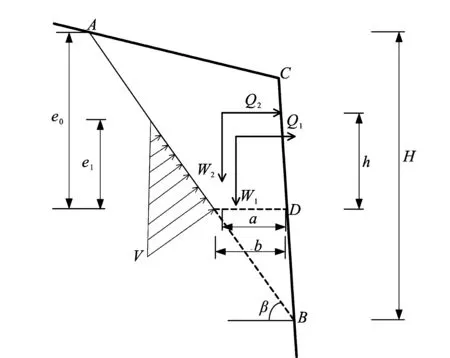
图4 危岩体稳定性计算图Fig.4 Calculation diagram for stability of unstable rock
裂隙水压力:
(8)
式中:γw为水的重度。
工程安全级别取一级,根据式(5)~式(7)可得:
c=95.06 kPa;φ=17.0°;V=135.2 kN。
没有地震力作用时,由于危岩体的重心点在倾覆点D以内,其破坏模式只可能为滑塌式破坏,但是由于地震力的作用,其破坏模式有可能由滑塌式破坏转化为倾倒式破坏。即在地震作用下,该危岩体可能存在两种破坏模式。
假设危岩体的破坏模式为滑塌式破坏,则其应沿着AB滑面滑动破坏,其稳定性系数为
(9)
如果危岩体的破坏模式为倾倒式破坏,则其应沿倾覆点D向外侧倾倒,此时危岩体的质量与滑塌式破坏时选取的质量不同,稳定性系数应为
(10)
设地震系数为ξ,则上面二式可表示成
假定除地震系数之外的参数均为已知量,代入参数进行计算可得
(11)
(12)
以往的研究表明,危岩的响应地震加速度可以达到输入地震加速度的几倍甚至几十倍[13-15]。而对于我国的四川、甘肃、新疆等部分地区,设计基本地震加速度不低于0.40g,如果危岩所在地区的设计地震加速度取0.5g,则危岩实际可能的响应地震加速度可能达到2g甚至更大。地震系数分别取0.05,0.10,…,0.50,按不同破坏模式计算得到的安全系数如表2所列。
从表中可以看出,在地震系数ξ<0.20时,按照两种破坏模式进行计算,边坡的安全系数均满足稳定状态;当0.20<ξ<0.25时,按照滑塌式破坏计算,危岩体处于欠稳定状态,按照倾倒式破坏计算,危岩体处于稳定状态,此时一般认为危岩体破坏模式为滑移式破坏;随着地震系数的增大,按照滑移式破坏计算的安全系数开始大于按照倾倒式破坏计算的安全系数,当0.40≤ξ≤0.45时,危岩体的安全系数F1>1,同时F2<1,这时可以认为边坡由滑移式破坏转变为倾倒式破坏。因此判断危岩体的破坏模式时,需要考虑地震系数的影响。
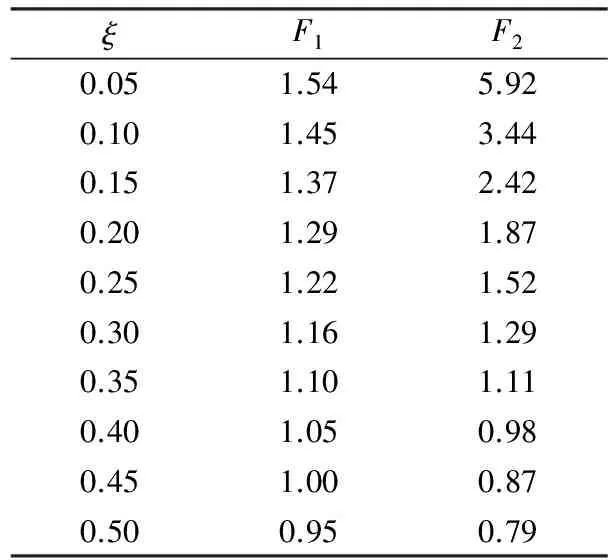
表 2 不同地震系数下不同计算方法稳定性系数
令F1=F2,易知方程存在两个解,即ξ1和ξ2,此时按照两种模式计算的安全系数相等。考虑山体对场地地震加速度的放大作用,地震加速度取值至3.0g,将表2转化成图5所示的曲线,可以看出两种破坏模式下安全系数随地震系数增加的变化趋势。
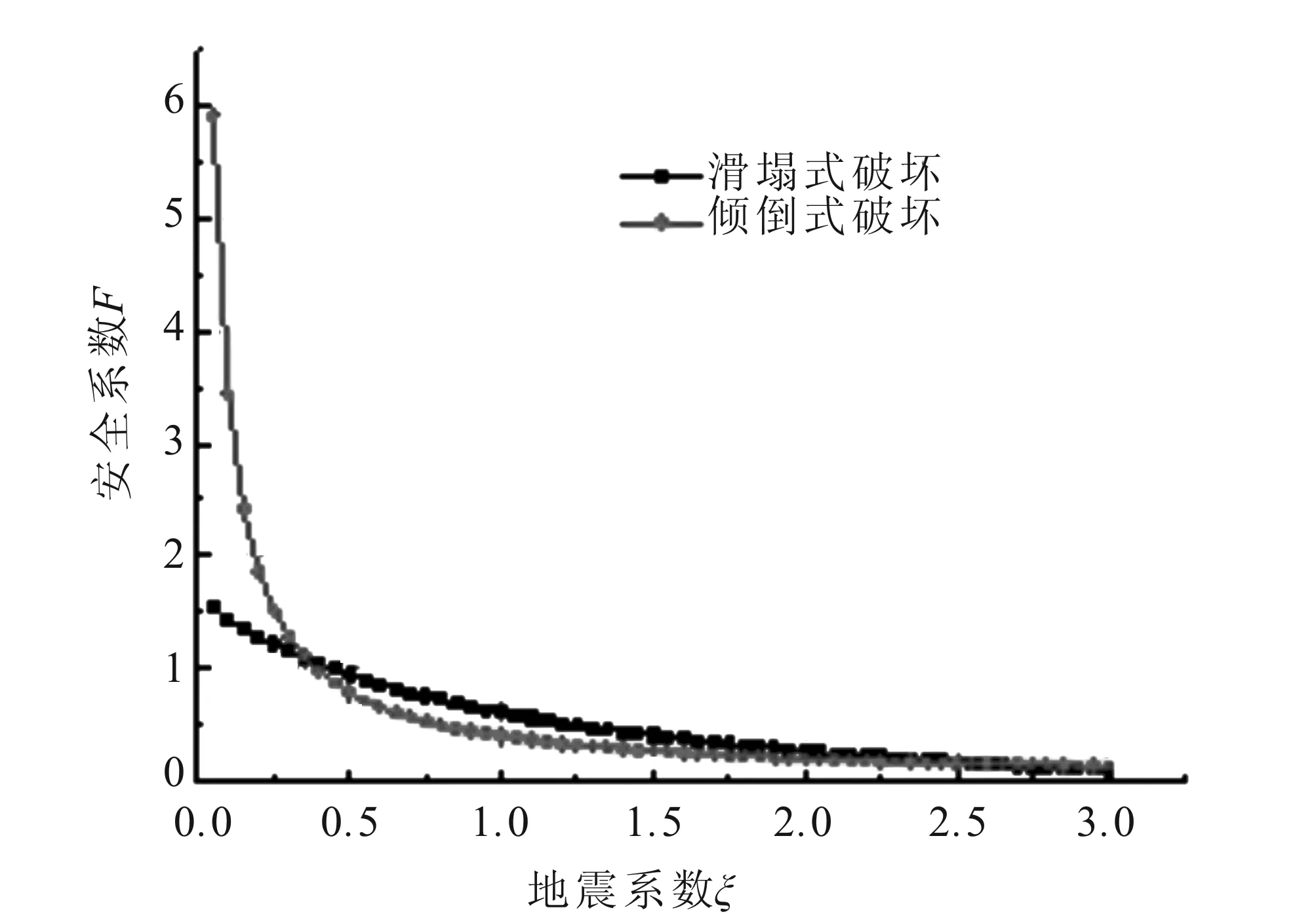
图5 不同地震系数下的安全系数Fig.5 Safety factors at different seismic coefficients
从图中可以得出,安全系数为关于地震系数的单调递减函数,但两种模式下危岩体的安全系数随地震系数的增大其衰减的速率并不一致。在地震系数较低时,倾倒式破坏的安全系数较大,但其衰减呈现先快后慢的趋势;滑塌式破坏的安全系数呈近似线性衰减,衰减的速率整体相对较慢。这说明地震作用对危岩的倾覆力矩贡献相对较大。
一般来说,地震系数确定以后,先计算并比较两种破坏模式计算的安全系数大小,认为安全系数较小者即为危岩体的可能破坏模式。然而从图5中可以看出选取不同的地震系数,不同模式的安全系数之间的大小并不确定,在不同区间内存在不同的关系:当ξ<ξ1时,F1 2.2 结果分析 根据上节中的算例分析,考虑一般情况下,安全系数为1时所对应的地震系数所处的不同区间,两种模式下计算的安全系数在理论上存在以下4种可能情况(图6)。 图6 4种可能的情况Fig.6 Four possible cases 在图6(a)中,除非选择的地震系数足够大,否则危岩体的安全系数始终大于1;图6(b)中,地震系数在ξ>ξ2区间内某一点之后,出现了安全系数小于1的情况;图6(c)中,地震系数在ξ>ξ1之后的某个位置后,安全系数开始小于1;图6(d)中,地震系数在ξ<ξ1区间内即出现了安全系数小于1的情况。第一种情况可以认为危岩体在地震作用下不会发生破坏。后面的三种情况下,地震系数确定之后,可以确定不同破坏模式下安全系数之间的大小,显然,直接以安全系数较小的破坏模式作为危岩体的破坏模式是不恰当的。 以图6(c)为例,如果选择的地震系数ξ>ξ2,此时F1 如果地震系数等于ξ1或ξ2,此时不同破坏模式进行计算的安全系数相等,若安全系数恰好为1,则应根据安全系数在这一点的一阶导数进行判断,由于安全系数是关于地震系数的减函数,所以应选择一阶导数较小者作为危岩体的破坏模式。 值得注意的是,根据安全系数先到达1作为标准可以判断危岩体的破坏模式,但是也会出现不同破坏模式下计算的安全系数均小于1。因此,不仅需要在已确定的破坏模式下进行计算,同时要对其他破坏模式下进行校核计算,以保证危岩体不会发生其他破坏模式的破坏。另外,出于描述的简洁,本文算例中仅取一种工况进行计算,裂隙水高度取1/3的后缘裂隙高度。对其他工况,如暴雨条件下,裂隙水高度取值更大,或者围岩的类别也会影响稳定性计算中参数的取值,但并不会影响文中讨论的两种破坏模式计算公式的曲线类型,因而不会影响本文所得到的一般性规律。 考虑到地震加速度在地震作用过程中是变化的,如果根据静力状态下判断的危岩体破坏模式对危岩体的地震稳定性进行评价,可能导致错误的结果,给抗震加固工程带来安全隐患。本文采用拟静力法,考虑地震作用过程中地震加速度的变化,通过对一工程实例进行分析,并扩展至一般情况进行讨论,对危岩体的地震动力稳定性进行评价,得到以下结论: (1) 按照不同破坏模式计算的危岩体的安全系数不同;在不同强度的地震作用下同一危岩体的破坏模式可能不同。在同一地震作用过程中,由于地震加速度是变化的,同一危岩体也可能存在不同的破坏模式,且可能在滑塌式破坏和倾倒式破坏之间相互转化。 (2) 危岩体安全系数为关于地震系数的单调递减函数,地震力对危岩体破坏的作用贡献不同,通常情况下,地震作用力对危岩的倾覆力矩贡献相对较大。 (3) 对危岩体进行抗震加固设计时,地震系数的取值应从0至设计值区间进行校核,依据不同破坏模式的稳定性计算公式,保证危岩体在整个地震作用过程中的稳定性。 References) [1] Baker R,Garber M.Theoretical Analysis of the Stability of Slopes[J].Geotechnique,1978,28(4):395-411. [2] Baker R,Shukha R,Operstein V,et al.Stability Charts for Pseudo-static Slope Stability Analysis[J].Soil Dynamics and Earthquake Engineering,2006,26(9):813-823. [3] Baker R.Sufficient Conditions for Existence of Physically Significant Solutions in limiting Equilibrium Slope Stability Analysis[J].International Journal of Solids and Structures,2003,40(13):3717-3735. [4] Li A J,Lyamin A V,Merifield R S.Seismic Rock Slope Stability Charts Based on Limit Analysis Methods[J].Computers and Geotechnics,2009,36(1):135-148. [5] Hack R,Alkema D,Kruse G A M,et al.Influence of Earthquakes on the Stability of Slopes[J].Engineering Geology,2007,91(1):4-15. [6] 苏晓成,周天来,刘志峰.拟静力法公路路基结构抗震稳定性研究[J].地震工程学报,2014,36(3):482-488. SU Xiao-cheng,ZHOU Tian-lai,LIU Zhi-feng.Seismic Stability Analysis of Highway Subgrade Based on the Pseudo-static Method[J].China Earthquake Engineering Journal,2014,36(3):482-488.(in Chinese) [7] 刘才华,陈从新.地震作用下岩质边坡块体倾倒破坏分析[J].岩石力学与工程学报,2010,29(增刊1):3193-3198. LIU Cai-hua,CHEN Cong-xin.Analysis of Toppling Failure of Rock Slopes due to Earthquakes[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(Supp1):3193-3198.(in Chinese) [8] 刘红帅,薄景山,杨俊波.确定岩质边坡地震安全系数的简化方法[J].岩石力学与工程学报,2012,31(6):1107-1114. LIU Hong-shuai,BO Jing-shan,YANG Jun-bo.Simplified Method for Determing Seismic Safety Factor of Rock Slope[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(6):1107-1114.(in Chinese) [9] 李维光,张继春.地震作用下顺层岩质边坡稳定性的拟静力分析[J].山地学报,2007,25(2):184-189. LI Wei-guang,ZHANG Ji-chun.Equivalent Static Stability Study on Rock Mass Bedding Slope under Blasting[J].Journal of Mountain Science,2007,25(2):184-189.(in Chinese) [10] 陈洪凯,王蓉,唐红梅.危岩研究现状及趋势综述[J].重庆交通学院学报,2003,22(3):80-88. CHEN Hong-kai,WANG Rong,TANG Hongmei.Review on Current Situation to Study and Trend of Dangerous Rock Mass[J].Journal of Chongqing Jiaotong University,2003,22(3):80-88.(in Chinese) [11] 陈洪凯,鲜学福,唐红梅,等.危岩稳定性分析方法[J].应用力学学报,2009,26(2):278-282. CHEN Hong-kai,XIAN Xue-fu,TANG Hong-mei,et al.Stability Analysis Method for Perilous Rock[J].Chinese Journal of Applied Mechanics,2009,26(2):278-282.(in Chinese) [12] 重庆市建设委员会.DB50143-2003,地质灾害防治工程勘察规范[S].重庆,2003. Chongqing Municipal Construction Commission.DB50143-2003,Code for Geological Disaster Prevention Engineering Survey[S].Chongqing,2003.(in Chinese) [13] 何蕴龙,陆述远.岩石边坡地震作用近似计算方法[J].岩土工程学报,1998,20(2):66-68. HE Yun-long,LU Shu-yuan.A Method for Calculating the Seismic Action in Rock Slope[J].Chinese Journal of Geotechnical Engineering,1998,20(2):66-68.(in Chinese) [14] 孙博,彭宁波,王逢睿.云冈石窟第19窟西耳窟地震动力响应[J].西南交通大学学报,2012,47(4):573-579. SUN Bo,PENG Ning-bo,WANG Feng-rui.Seismic Dynamic Responses of No.19 Grotto’s West Side Cave of Yungang Grottoes[J].Journal of Southwest Jiaotong University,2012,47(4):573-579.(in Chinese) [15] 祁生文,伍法权,刘春玲,等.地震边坡稳定性的工程地质分析[J].岩石力学与工程学报,2004,23(16):2792-2797. QI Sheng-wen,WU Fa-quan,LIU Chun-ling,et al.Engineering Geology Analysis of Stability of Slope under Earthquake[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(16):2792-2797.(in Chinese) Failure Mode and Stability Evaluation of Unstable Rock during Earthquakes PENG Ning-bo1, SUN Bo2, WANG Feng-rui2, 3, XIA Jiang-tao1 (1.FacultyofArchitectureandCivilEngineering,HuaiyinInstituteofTechnology,Huaian223021,Jiangsu,China; 2.NorthwestResearchInstituteCo.Ltd.ofChinaRailwayEngineeringCorporation,Lanzhou730000,Gansu,China; 3.KeyLaboratoryofMechanicsonDisasterandEnvironmentinWesternChinaoftheMinistryofEducation,SchoolofCivilEngineeringandMechanics,LanzhouUniversity,Lanzhou730000,Gansu,China) During seismicity, seismic acceleration first increases then decreases. Using a pseudo-static method and considering the acceleration change during earthquakes, sliding and toppling failure modes were calculated for the unstable rock on Tianlong mountain, Taiyuan city, Shanxi province. We found that the failure mode transformed from sliding to toppling under seismic action. Extending this problem to a general situation, we conclude that: the contribution of seismic forces to unstable rock damage differs and the overturning moment is relatively larger than the sliding force; for stability evaluation, the seismic action process must be considered, and the failure mode of unstable rock whose safety factor first reaches 1.0 should be used to calculate the possible mode; to ensure the stability of unstable rock of different risk states under seismic action, the seismic strengthening design should consider different possible failure modes. pseudo-static method; seismic process; unstable rock; failure mode; stability 2015-10-12 基金项目:甘肃省科技厅科技支撑计划课题(1304FKCA119) 彭宁波(1986-)男,博士,讲师,现主要从事岩石力学、边坡工程及文物加固保护方面的教学研究工作。 E-mail:pengnb10@lzu.edu.cn。 TU457 A 1000-0844(2016)06-0916-06 10.3969/j.issn.1000-0844.2016.06.0916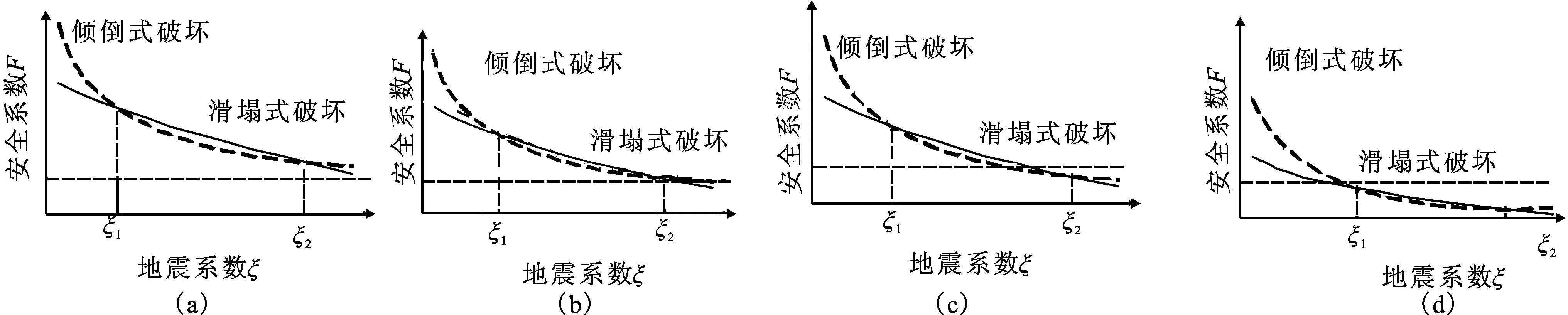
3 结论
