基于流固耦合动力模型的饱和土体-隧道体系地震反应研究

李 亮, 吴利华, 王相宝, 高 超

(北京工业大学城市与工程安全减灾教育部重点实验室,北京 100124)

基于流固耦合动力模型的饱和土体-隧道体系地震反应研究

李 亮, 吴利华, 王相宝, 高 超

(北京工业大学城市与工程安全减灾教育部重点实验室,北京 100124)

基于ABAQUS软件平台,应用自行开发的流固耦合动力模型孔压单元模拟场地土体,并通过黏弹性人工边界方法实现地震动的输入,对饱和土体场地中的双孔隧道结构在地震荷载作用下的动力反应进行研究。计算结果表明：在地震反应结束时刻,场地土体位移幅值在两隧道之间以及两隧道的附近区域较大,而远离隧道的区域则较小;场地底部区域土体的孔压幅值较大,而场地顶部区域土体则较小;隧道左右两侧拱腰部位的衬砌的应力较大,而拱顶部位则较小。计算结果同时表明了流固耦合动力模型孔压单元在饱和土体-隧道体系地震反应研究中的适用性。

饱和土体; 隧道; 地震反应; 流固耦合动力模型; 黏弹性人工边界

0 引言

随着我国社会经济的快速发展,城市规模日益扩大,对交通设施的发展提出了更高的要求。在地面交通日趋饱和的前提下,大力发展地下交通成为缓解交通压力的有效途径。在我国的许多沿海和沿江城市,为满足不同区域之间地下交通连接的需要,已兴建了多条跨海、越江和水下隧道工程,如厦门翔安海底隧道、青岛胶州湾海底隧道、武汉长江隧道、南京玄武湖隧道及杭州西湖隧道等。跨海和越江隧道的修建对缓解城市干道的交通压力,加强港湾两岸的交通联系都起着重要作用。

我国地处环太平洋地震带上,在全国近300个城市中,有近一半处于地震烈度Ⅶ度或Ⅶ度以上的地震区,因此跨海、越江和水下隧道工程必将面临潜在的地震威胁,这类工程结构的抗震安全性是一个必须加以重视的问题。解决上述问题首先需进行此类工程结构的地震响应计算,以计算结果作为抗震设计的基础和依据。这类结构修建在水下饱和沉积土层中,由于其所处的特殊介质条件,其在地震荷载作用下动力反应的性质将与一般土层中的隧道结构具有显著的不同。研究这类结构的地震反应问题必须考虑结构本身与周围饱和土体介质的动力相互作用进行整体的计算和分析。

针对饱和土体-隧道体系动力问题的研究方法可以分为理论和解析方法[1-3]、模型试验方法[4-5]和数值计算方法三大类,其中数值计算方法应用最为广泛。根据所采用的场地土体力学分析模型,数值计算方法又可分为总应力法[6-7]、简化的有效应力法[8-9]和基于流固耦合动力模型的分析方法[10-11]三类。简化的有效应力方法的计算过程中需根据土体固相的变形,采用假定的孔压模式确定孔隙流体的动力响应。该方法不能实现土体固相与孔隙流体动力反应的相互耦合,因此只是一种近似的计算方法。流固耦合动力模型是一种比较完善的理论计算模型,它可以实现饱和土体中固相和液相(孔隙流体)动力反应之间的相互耦合,因此基于该模型的方法是一种比较精确的计算分析方法。目前,基于流固耦合动力模型的饱和土体场地中隧道结构动力反应特性的研究还有待进一步深入和完善。同时,这类问题的数值计算通常需要借助于一定的软件平台,如ABAQUS、FLAC、ANSYS等才能完成,因此流固耦合动力模型需在特定的软件平台上加以实现。笔者在前期的研究工作中[12],已经基于ABAQUS软件平台开发了用于饱和土体动力问题计算研究的流固耦合动力模型孔压单元,完成了流固耦合动力模型的软件实现。

本文将在前期研究工作的基础上,基于ABAQUS有限元软件平台,开展基于流固耦合动力模型的饱和土体-隧道体系地震反应研究,以获得对饱和土体场地中隧道结构地震反应特性的较为全面的认识。

1 流固耦合两相介质动力模型及其软件实现

流固耦合两相介质动力模型的数学表达式为u-p形式的两相介质动力方程[13],该方程以固相的位移u和液相(孔隙流体)的压力p为基本未知量,其经过有限元空间离散后的表达形式为:

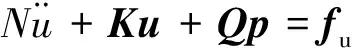
(1)

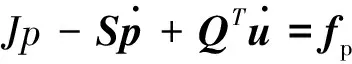
(1)

上述方程组适用于动力荷载频率较低的情况。式中:M为质量矩阵;K为刚度矩阵;Q为耦合矩阵;S为流体压缩矩阵;J为渗透矩阵;fu和fp分别为与固相位移和流体压力相关的边界荷载向量。上述各矩阵的表达式为：

K=∫Ω(LNu)TD(LNu)dΩ

Q=∫Ω(LNu)Tm(LNu)dΩ

J=k∫Ω(Np)T(Np)dΩ

式中：Nu为固相位移插值函数;Np为流体压力插值函数;ρ为饱和两相介质的质量密度;α和Qb为固相和液相压缩性相关系数,α=1-KD/KS,1/Qb=n/Kf-(1-α)/KS,KD=ES/[3(1-2ν)],KD为土骨架体积模量,KS为土颗粒体积模量,Kf为孔隙流体体积模量,ES为土骨架压缩模量,n为孔隙率,ν为泊松比,k为渗透系数;m为转换向量,m=[110]T;L为微分算子;为梯度算子;D为系数矩阵;针对二维动力问题,L、D、的具体表达式为：

式(1)和(2)规定了饱和土体中固相和液相的动力反应,即固相位移和孔隙流体压力之间的耦合关系。

笔者开发的孔压单元适用于二维动力问题的计算与分析,单元的节点数为4,每个节点的自由度数目为3,分别为水平位移自由度u1、竖向位移自由度u2和孔压自由度p;材料参数为3,分别为弹性模量E,泊松比ν,孔隙比n。通过在ABAQUS输入文件(.inp)中添加相应的关键字实现主程序对该单元的调用,在ABAQUS输入文件(.inp)中添加的相应的关键字为：

*User Element,Nodes=4,Type=U1001,

Properties=3,Coordinates=2,VARIABLES=64

*Element,type=U1001,Elset=UEL

*Uel Property,Elset=UEL

本文流固耦合两相介质动力模型孔压单元相应的程序开发以及算例验证工作请参见文献[12]。

2 基于流固耦合两相介质动力模型的饱和土体-隧道体系地震反应研究

基于ABAQUS有限元计算分析软件平台,以前期研究中开发的流固耦合两相介质动力模型孔压单元模拟场地饱和土层,对饱和土体-隧道体系的地震反应进行计算研究。以天津宁河地震南北方向分量的地震记录作为地震输入,其加速度时程和位移时程如图1所示。该地震记录的持续时间为19.2 s。

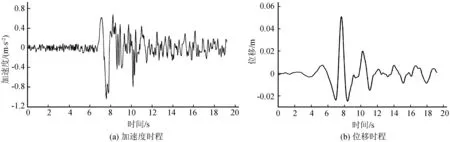
图1 输入地震记录加速度及位移时程Fig.1 Time history of the acceleration and displacement of input seismic record

2.1 计算模型与输入参数

算例的计算模型为饱和土体场地与其中的双孔隧道结构组成的体系。场地水平方向取200 m,竖直方向取80 m。两隧道中心间距为70 m,隧道直径为9 m,衬砌厚度为0.5 m,隧道上覆土层厚度为15 m,隧道外边缘距离近侧土体的距离均为55 m。隧道衬砌采用C50混凝土,密度取为2 500 kg/m3,弹性模量取为34.5 GPa,泊松比为0.18;场地饱和土体的密度为2 000 kg/m3,弹性模量为200 MPa,泊松比为0.3,孔隙率为0.3,土体的渗透系数为1×10-4m/s,孔隙水的体积压缩模量为2.0 GPa。

场地饱和土体采用笔者自行开发的二维流固耦合两相介质动力模型孔压单元进行模拟,隧道采用ABAQUS软件中提供的四边形实体单元进行模拟。场地土体的网格尺寸大部分为5 m×5 m,隧道附近的土体进行了网格加密。完成网格划分后的饱和土体-隧道体系的有限元计算模型如图2所示,计算体系的单元总数为1 464,节点总数为4 539。选取场地土体中的节点1～4以及隧道衬砌上的单元A、B、C、D为研究对象。节点1位于两隧道之间的区域,节点2位于右侧隧道下方区域,节点3位于右侧隧道右方区域,节点4位于左侧隧道左方区域。单元A和B分别位于左侧隧道衬砌的左侧拱腰和拱顶部位,单元C和D分别位于右侧隧道衬砌的右侧拱腰和拱底部位。

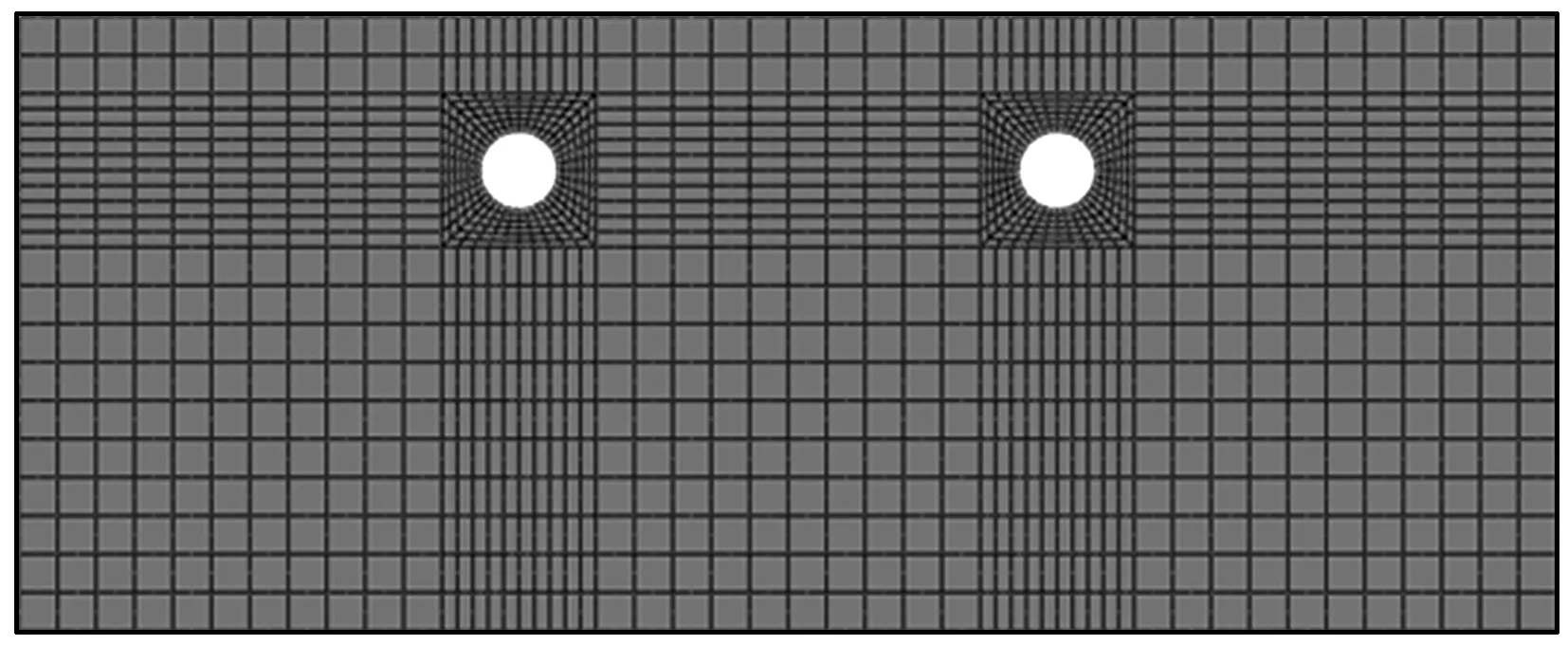
图2 饱和土体-隧道体系动力反应有限元计算模型Fig.2 Finite element model for dynamic response of the saturated soil-tunnel system

2.2 地震动输入方式

通过在计算模型的边界处设置黏弹性人工边界,将输入地震动转化为作用于黏弹性人工边界节点上的等效荷载的方法来实现地震动输入。等效节点荷载的计算采用王苏等[14]提出的方法,即通过引入无限介质的线弹性本构关系,建立一维平面波转化为应力人工边界输入时的等效节点荷载的表达式。转化的关键在于由已知的入射平面波时程确定内行场中波的时程和波在传播过程中引起的介质内力以及边界表面的应力时程。

本文输入的地震波为沿水平x向的SV波。

2.3 计算结果及分析

地震反应不同时刻(t=1 s、t=9 s、t=19.2 s)场地土体的孔压云图如图3(a)所示,竖向位移云图如图3(b)所示。场地中节点1～4的孔压时程和竖向位移时程如图4所示。

由图3可知，在地震反应的不同时刻，场地土体的孔压与竖向位移的空间分布具有相似的规律，仅是数值大小存在差异。在地震反应结束时刻，场地土体竖向位移值在两隧道之间以及两隧道的附近区域较大，而远离隧道的区域位移值较小；场地土体的孔压大致呈现分层分布，场地底部区域的孔压值较大,而场地顶部区域则较小。由图4(a)可知,位于场地不同区域的节点1、2、3及4的孔压时程的变化规律比较相似,但各节点的孔压峰值不同,分别为74 kPa、235 kPa、100k Pa及130 kPa,即位于两隧道之间区域的节点1孔压峰值最小,而位于隧道下方区域的节点2孔压峰值最大。由图4(b)可知,场地土体不同区域节点的位移时程的变化规律比较相似,且与输入地震动位移时程的波形近似一致。各节点位移峰值不同,节点1、2、3及4的位移峰值分别为9 cm、10 cm、10.5 cm及7 cm,即位于右侧隧道右方区域的节点3位移峰值最大,而位于左侧隧道左方区域的节点4位移峰值最小。

地震反应不同时刻(t=1 s、9 s及19.2 s)左右两侧隧道衬砌的应力云图如图5所示,各图中左右两个小图分别为该时刻左侧与右侧隧道衬砌的应力云图。隧道衬砌上单元A、B、C、D的应力时程如图6所示。

由图5可知,在地震反应的不同时刻,隧道衬砌的应力分布具有相似的规律,仅是数值大小存在差异。在地震反应结束的时刻,左右两侧隧道衬砌的应力呈镜像对称分布。对于每一侧的隧道而言,左右两侧拱腰部位的衬砌应力较大,而拱顶部位较小。由图6可知,左侧隧道衬砌上的单元A与单元B在应力峰值之前其应力反应时程的规律比较接近,而峰值之后其应力反应时程的规律有一定的差异。二者的应力峰值不同,单元A约为2.75 MPa,而单元B约为5.47 MPa。右侧隧道衬砌上的单元C与单元D的应力反应时程也具有相似的特点。单元C的应力峰值约为5.44 MPa,单元D约为3.60 MPa。

图3 地震反应不同时刻场地土体孔压云图及竖向位移云图Fig.3 Nephograms of the pore pressure and vertical displacement of site soil at different moment of seismic response

图4 场地土体不同区域节点孔压时程及竖向位移时程Fig.4 Time history of the pore pressure and vertical displacement of nodes located in different regions of site soil

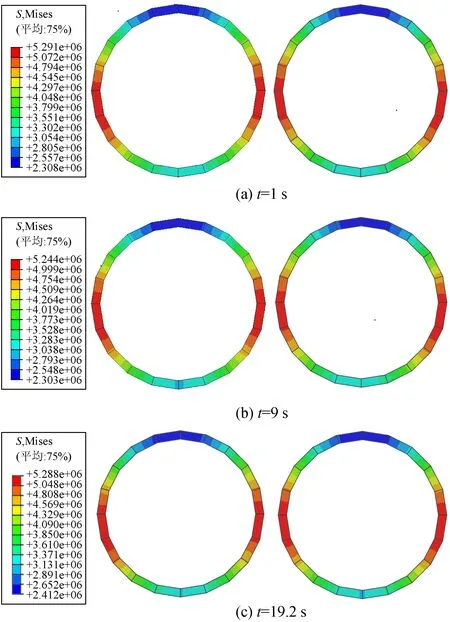
图5 地震反应不同时刻隧道衬砌应力云图Fig.5 Nephogram of the stress of tunnel lining at different moment of seismic response

4 结语

本文基于ABAQUS有限元计算软件平台,开展了基于流固耦合动力模型的饱和土体-隧道体系地震反应研究。应用前期研究工作中开发的二维流固耦合两相介质动力模型孔压单元模拟场地饱和土体,并通过黏弹性人工边界方法实现地震动的输入,对饱和土体场地中的双孔隧道结构在地震荷载作用下的动力反应进行了计算研究,重点研究了土体的位移和孔压及隧道衬砌的应力。研究结果表明：

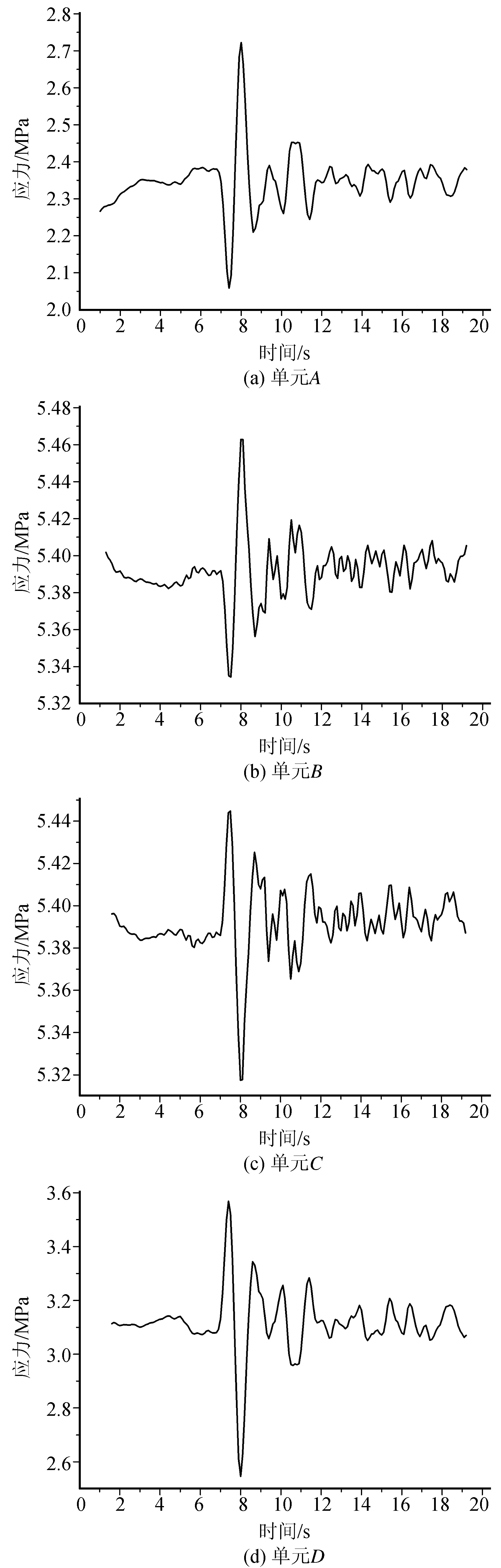
图6 隧道衬砌单元应力时程Fig.6 Time history of the stress of elements in the tunnel lining

(1) 在地震反应结束时刻,场地土体位移幅值在两隧道之间以及两隧道的附近区域较大,而在远离隧道的区域则较小;场地土体的孔压幅值大致呈现分层分布,场地底部区域的孔压幅值较大,而场地顶部区域则较小。

(2) 场地土体不同区域的位移和孔压反应时程的变化规律比较相似,但反应的峰值不同。

(3) 在地震反应结束时刻,左右两侧隧道衬砌的应力呈镜像对称分布。对于每一侧的隧道而言,左右两侧拱腰部位的衬砌应力较大,而拱顶部位的衬砌应力较小。

(4) 隧道衬砌不同部位在应力峰值之前的应力反应时程的规律比较接近,而峰值之后的应力反应时程的规律有一定的差异。隧道衬砌不同部位的应力峰值有所差异。

本文的研究工作同时表明了笔者开发的流固耦合两相介质动力模型孔压单元在饱和土体-地下结构体系动力问题计算研究中的适用性和可行性。

References)

[1] Bobet A.Effect of Pore Water Pressure on Tunnel Support during Static and Seismic Loading[J].Tunneling and Underground Space Technology,2003,18(4):377-393.

[2] 丁伯阳,党改红,袁金华.Green函数对饱和土隧道内集中荷载作用振动位移反应的计算[J].振动与冲击,2009,28(11):110-114. DING Bo-yang,DANG Gai-hong,YUAN Jin-hua.Application of Green Function in Calculation of Displacement Response of Saturated Soil Tunnel under Concentrated Load[J].Journal of Vibration and Shock,2009,28(11):110-114.(in Chinese)

[3] 赵江倩,刘优平,余巍伟,等.地震加速度作用下饱和土中深埋隧道的动力响应[J].岩土工程学报,2013,35(增刊1):418-424. ZHAO Jiang-qian,LIU You-ping,YU Wei-wei,et al.Dynamic Response of Deep Buried Tunnels in Saturated Soil to Effect of Seismic Acceleration[J].Chinese Journal of Geotechnical Engineering,2013,35(Supp1):418-424.(in Chinese)

[4] 陈国兴,庄海洋,杜修力,等.土—地铁隧道动力相互作用的大型振动台试验—试验结果分析[J].地震工程与工程振动,2007,27(1):164-170. CHEN Guo-xing,ZHUANG Hai-yang,DU Xiu-li,et al.A Large-scale Shaking Table Test for Dynamic Soil-metro Tunnel Interaction:Analysis of Test Results [J].Journal of Earthquake Engineering and Engineering Vibration,2007,27(1):164-170.(in Chinese)

[5] 刘光磊,宋二祥,刘华北,等.饱和砂土地层中隧道结构动力离心模型试验[J].岩土力学,2008,29(8):2070-2076. LIU Guang-lei,SONG Er-xiang,LIU Hua-bei,et al.Dynamic Centrifuge Tests on Seismic Response of Tunnel in Saturated Sandy Foundation[J].Rock and Soil Mechanics,2008,29(8):2070-2076.(in Chinese)

[6] 庄海洋,陈国兴.双洞单轨地铁区间隧道非线性地震反应分析[J].地震工程与工程振动,2006,26(2):131-137. ZHUANG Hai-yang,CHEN Guo-xing.Analysis of Nonlinear Earthquake Response of Metro Double-tunnels[J].Journal of Earthquake Engineering and Engineering Vibration,2006,26(2):131-137.(in Chinese)

[7] 李洪煊,蔡新,武颖利,等.水下公路隧道结构地震响应分析[J].地下空间与工程学报,2010,6(5):952-957. LI Hong-xuan,CAI Xin,WU Ying-li,et al.The Seismic Response Analysis of Under-water Tunnel[J].Chinese Journal of Underground Space and Engineering,2010,6(5):952-957.(in Chinese)[8] 张长泰,张玉芳.饱和砂土中的地铁圆形衬砌隧道地震响应分析[J].铁道工程学报,2008(1):76-80. ZHANG Chang-tai,ZHANG Yu-fang.Analysis of Seismic Response to the Metro Tunnel in Saturated Sand-soil Area[J].Journal of Railway Engineering Society,2008(1):76-80.

[9] 黄娟,彭立敏,李兴龙.可液化地层狮子洋盾构隧道横向地震响应规律及减震措施研究[J].岩土工程学报,2009,31(10):1539-1546. HUANG Juan,PENG Li-min,LI Xing-long.Transverse Seismic Responses of Shiziyang Shield Tunnel in Liquefiable Soil and Its Shock Absorption Measures[J].Chinese Journal of Geotechnical Engineering,2009,31(10):1539-1546.(in Chinese)[10] 刘光磊,宋二祥,刘华北.可液化地层中地铁隧道地震响应数值模拟及其试验验证[J].岩土工程学报,2007,29(12):1815-1822. LIU Guang-lei,SONG Er-xiang,LIU Hua-bei.Numerical Modeling of Subway Tunnels in Liquefiable Soil under Earthquakes and Verification by Centrifuge Tests[J].Chinese Journal of Geotechnical Engineering,2007,29(12):1815-1822.(in Chinese)[11] 李伟华.考虑水-饱和土场地-结构耦合时的沉管隧道地震反应分析[J].防灾减灾工程学报,2010,30(6):607-613. LI Wei-hua.Seismic Response Analysis of Immersed Tube Tunnel Considering the Dynamic Interactions between Water,Stratum and Structure[J].Journal of Disaster Prevention and Mitigation Engineering,2010,30(6):607-613.(in Chinese)[12] 李亮,崔智谋,康翠兰,等.流固耦合饱和两相介质动力模型在ABAQUS中的实现[J].岩土工程学报,2013,35(增刊2):281-284. LI Liang,CUI Zhi-mou,KANG Cui-lan,et al.The Fluid-solid Coupling Dynamic Model for Fluid-saturated Porous Media in ABAQUS[J].Chinese Journal of Geotechnical Engineering,2013,35(Supp2):281-284.(in Chinese)

[13] Zienkiewicz O C,Chang C T,Bettess P.Drained,Undrained,Consolidating and Dynamic Behaviour Assumptions in Soils[J].Geotechnique,1980,30(4):385-395.(in Chinese)

[14] 王苏,路德春,杜修力.地下结构地震破坏静-动力耦合模拟研究[J].岩土力学,2012,33(11):3483-3488. WANG Su,LU De-chun,DU Xiu-li.Research on Underground Structure Seismic Damage Using Static-dynamic Coupling Simulation Method[J].Rock and Soil Mechanics,2012,33(11):3483-3488.(in Chinese)

Seismic Response of Saturated Soil-tunnel System Based on Fluid-solid Coupling Dynamic Model

LI Liang, WU Li-hua, WANG Xiang-bao, GAO Chao

(KeyLaboratoryofUrbanSecurityandDisasterEngineering,MinistryofEducation,UniversityofTechnology,Beijing100124,China)

In this study, we used ABAQUS software to calculate the seismic response of a twin-bore tunnel in a saturated soil deposit. To simulate the saturated soil deposit, we employed a pore pressure element based on a fluid-solid coupling dynamic model for fluid-saturated porous media, and we input earthquake motion into the calculation model by a visco-elastic artificial boundary. Our numerical results show that at the end of the seismic response the displacement amplitudes of the soil between the two tunnels and near the tunnels is relatively large, while that far away from the tunnels is small. In addition, at the end of the seismic response, the pore pressure amplitude of the soil deposit at the bottom area of the site is relatively large, while that at the top is small. The stress of the tunnel lining at both tunnel arch waists is relatively large, while that in the tunnel vault is small. With respect to the study of the seismic response of tunnels in saturated soil deposits, we verified the applicability of the pore pressure element based on a fluid-solid coupling dynamic model for fluid-saturated porous media.

saturated soil; tunnel; seismic response; fluid-solid coupling dynamic model; visco-elastic artificial boundary

2016-04-25 基金项目：国家自然科学基金面上项目(51178011)；国家重点基础研究发展计划973计划项目(2011CB013602) 作者简介：李 亮，男，副教授，硕士生导师，主要从事土动力学理论与数值计算方面的研究。E-mail：liliang@bjut.edu.cn。

TU354

A

1000-0844(2016)06-0862-07

10.3969/j.issn.1000-0844.2016.06.0862