3T2R混联机构运动学性能分析

曹浩峰，曹 毅，陈 海，秦友蕾，丁 锐

(1. 江南大学 机械工程学院， 江苏 无锡 214122;2. 江苏省食品先进制造装备技术重点实验室， 江苏 无锡 214122;3. 宁波广播电视大学， 浙江宁波 315100；4. 上海交通大学 机械系统与振动国家重点实验室， 上海 200240)

3T2R混联机构运动学性能分析

曹浩峰1,2,3，曹 毅1,2,4，陈 海1,2，秦友蕾1,2，丁 锐1,2

(1. 江南大学 机械工程学院， 江苏 无锡 214122;2. 江苏省食品先进制造装备技术重点实验室， 江苏 无锡 214122;3. 宁波广播电视大学， 浙江宁波 315100；4. 上海交通大学 机械系统与振动国家重点实验室， 上海 200240)

5自由度混联机构由完全各向同性的三维移动并联机构和2自由度转动的串联机构组成.此混联机构末端位置由两部分共同决定，姿态完全由串联部分决定.首先，求解了机构的自由度数目，并运用螺旋理论分析了自由度性质.然后，选取机构的驱动副，判断并联模块支链第5个转动副为消极副，从而简化了并联模块，方便了后续的分析.最后，分析了混联机构的运动学特征，利用运动影响系数求得其速度雅可比矩阵，并分析了机构的工作空间和奇异位形.该机构运动学解耦，计算方便，便于实时运动控制，同时机构工作空间大，无奇异位形，有很好的应用前景.

混联机构； 螺旋理论； 运动学； 工作空间； 奇异位形

混联机器人兼具串联机器人的工作空间大、易于控制，以及并联机器人的结构稳定、刚性好、累积误差小、动态性能好、精度高的优点，同时又能避免单纯串、并联机器人所带来的问题，其在现代制造业中更具有实用性，是今后机构学研究的一个重要发展方向[1-3].文献[4]研制了6轴混联式数控机床；文献[5]对3杆混联数控机床的运动学进行了研究；德国DMG 公司的著名五轴联动机床DMC 165加工中心采用3个方向的平动轴构成的龙门加双摆头的串联结构[6-7]；文献[8]研制了多喷枪协同式五轴混联机器人；文献[9]运用PARAMIS并联模块和串联模块研发了一种新型手术机构.

少自由度并联机构设计与创新是混联机构设计的一个重要前提[10].解耦的并联模块，其输入、输出没有耦合，则其理论分析和控制得到简化[11].本文提出的5自由度混联机器人，其由3自由度完全各向同性的三移并联模块和2自由度转动串联模块组成.并联模块由3条正交分布的支链把动平台和静平台连接起来，在空间三维移动方向解耦，所以整个混联机构不存在耦合.机构正逆解简单，工作空间大，结构和控制简单，具有良好的应用前景.

1 混联机构的描述

位置分析是研究机器人末端执行器位姿与各个轴转角之间的关系，包括位置正解和逆解两部分.

此混联机构由并联模块3PRRPR和串联模块2R构成，其中，并联模块3PRRPR如图1所示，它由3条支链将动平台和静平台相连.每条PRRPR分支都具有5个自由度.其中，2条支链完全相同，将每个分支的每个运动副进行编号，可以表示成第i条支链的第j个运动副.第1个移动副Pi1平行于第2个转动副Ri2和第3个转动副Ri3的轴线，第4个移动副Pi4与第5个转动副Ri5平行，并且Pi1和Pi4相互垂直(i=1,3).对于第2条支链，第1个移动副P21平行于第2个转动副R22和第3个转动副R23的轴线，第4个移动副P24与第5个转动副R25及P21相互垂直.

3条支链的第一个移动副在空间中呈正交布置，按照图1所示建立空间直角坐标系，则P11平行于Z轴，P21平行于X轴，P31平行于Y轴.串联模块的第1个转动副轴线平行于动平台平面，第2个转动副垂直于动平台，并且2个转动副轴线互相垂直.

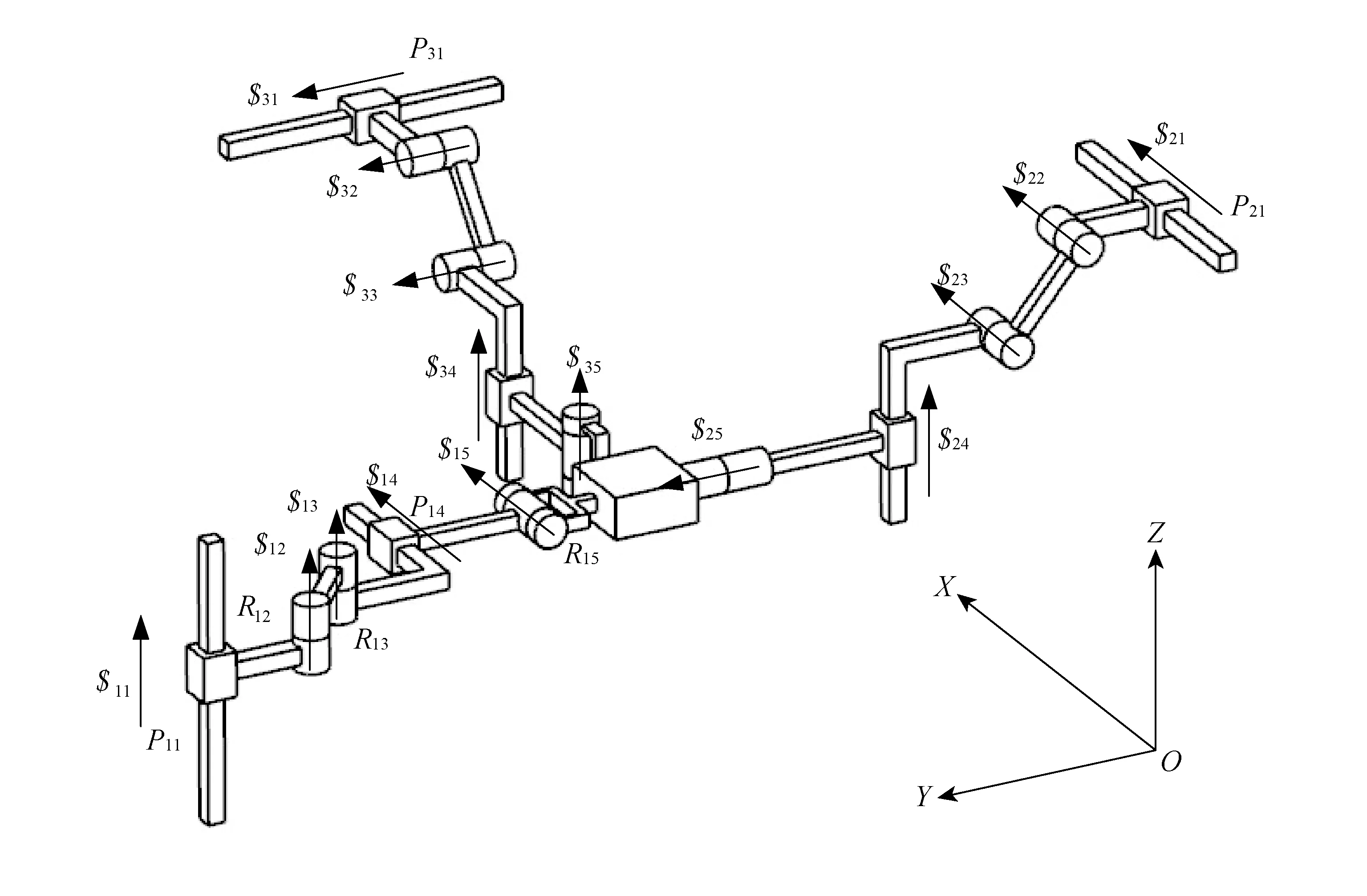
图1 3-PRRPR并联机构Fig.1 3-PRRPR parallel mechanism

2 混联机构自由度分析

2.1 混联机构自由度数计算

运用修正的Grübler-Kutzbach通用自由度计算公式[12](如式(1) )进行混联机构自由度数计算.

6×(16-17-1)+17=5

(1)

式中：M为机构自由度；d为机构阶数；n为包括机架的构件数目；g为运动副的数目；fi为第i个运动副的自由度；μ为机构中过约束的总数；ζ为机构中存在的局部自由度.

2.2 混联机构自由度性质分析

对于混联机构中的并联模块，如图1用＄ij表示第i条支链的第j个运动副的运动螺旋.lij、mij、nij、pij、qij、rij表示第i条支链的第j个运动副的运动螺旋plüker坐标.

为分析混联机构自由度性质，选取第1条支链，其5个运动螺旋plüker坐标可表示为

(2)

(3)

同理，可以求得第2条支链的运动螺旋系的约束反螺旋是一个沿着Z轴方向作用到动平台上的约束力偶.第3条支链运动螺旋系的约束反螺旋是一个沿着X轴方向作用到动平台上的约束力偶.

从整个并联模块看，3条支链将会产生3个作用到动平台上的约束力偶，这3个力偶彼此线性无关，刚好约束了动平台上的3个转动自由度，所以此并联模块可以实现空间三维移动.再加上串联在动平台上的2个转动自由度，所以此混联机构具有三移两转5个自由度.

3 混联机构驱动选取

首先，选取并联模块的驱动.由于并联模块具有3个移动自由度，所以需要3个驱动.可采用基于螺旋理论的并联机构驱动选取方法.该方法为锁定选定的驱动，如果驱动选取正确，当驱动被限制的时候，动平台将失去全部的自由度，则动平台的约束螺旋系的最大线性无关数为6[13].

一般选择移动副或者转动铰作为驱动关节，由于移动副可以提高机构的精度指标并增加负载能力，因此，大多数3自由度并联机构在实际使用中都采用移动副作为驱动关节[14].对此机构，选取与静平台相连的3个在空间相互垂直的移动副为驱动.如限制这3个移动副后，对每条支链分别求取其运动螺旋的反螺旋，可得到动平台的约束螺旋系为

(4)

显然式(4)中的6个约束螺旋系线性无关，所以此时的动平台自由度为0，即当3个移动副被限制住后，动平台不能运动，所以驱动选取正确.

记动平台的角速度矢量为ωn，固定在动平台上的参考坐标系原点线速度矢量为vn，则动平台的运动螺旋为

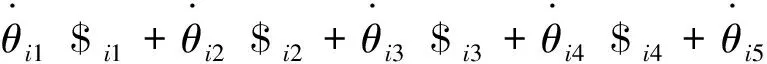
(5)

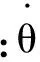
对于支链1，将将运动螺旋系代入式(5)中，可得：

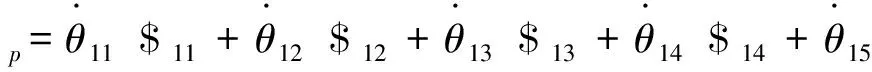
(6)

由于并联模块只有三维移动自由度，所以ωn=[0 0 0]T，代入式(6)中可得：

(7)

由此可以看出支链1的第5个转动副R15的转动角速度为0.同理可得支链2和支链3的第5个转动副R25和R35的转动角速度为0.

因此，并联模块各支链的第5个转动副在机构发生运动时均不发生转动，是个消极的运动副.并联机构可以简化为完全对称的3-PRRP机构，这样可以简化后续的运动学分析.

对于串联模块的2个自由度分别加2个转动驱动.

4 混联机构位置分析

4.1 并联模块位置分析

如图2所示，将固定坐标系O-XYZ设定在机架的右下方，动坐标系p-xyz设置在动平台的几何中心上.支链1中P11的起始点位于XY平面，距X轴D1x，距Y轴D1y，P11的输入位移为q11.支链2中P21位于XZ平面，它的起始点距X轴D2x，距Z轴D2z，P21的输入位移为q21.支链3中P31的起始点距YZ平面D3x，距XZ平面D3y，距XY平面D3z，P31的输入位移为q31.第1个移动副的行程为L1，它距离第2个转动副的距离为a，第2个转动副与第3个转动副的距离为L2，第3个转动副距离第4个移动副的起始端的距离为b，第4个移动副的行程为L3，第4个移动副距离动平台中心点的距离为c.在3条支链中，第2个转动副与第3个转动副的连线的转动角度分别为α1，β1，γ1，并规定此连线与第1个移动副和第2个转动副之间的构件垂直时为0°，顺时针旋转为正.

图2 并联模块运动参数示意图Fig.2 Kinematic parameters schematic of the parallel module

根据图2的几何关系，可得动平台中心点p的位置坐标.对于第1条支链：

(8)

对于第2条支链：

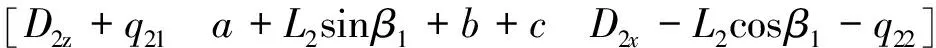
(9)

对于第3条支链：

p=[ D3x-a-L2sinγ1-b-c D3y+q31

D3z-L2cos γ1-q32]

(10)

由式(8)～(10)可得：

(11)

由此可以得到此并联机构的运动学正解为

(12)

由式(12)可以得到运动学的逆解为

(13)

4.2 串联模块位置分析

利用坐标系建立方法建立串联模块各连杆的坐标系如图3所示，对应的D-H参数如表1所示.

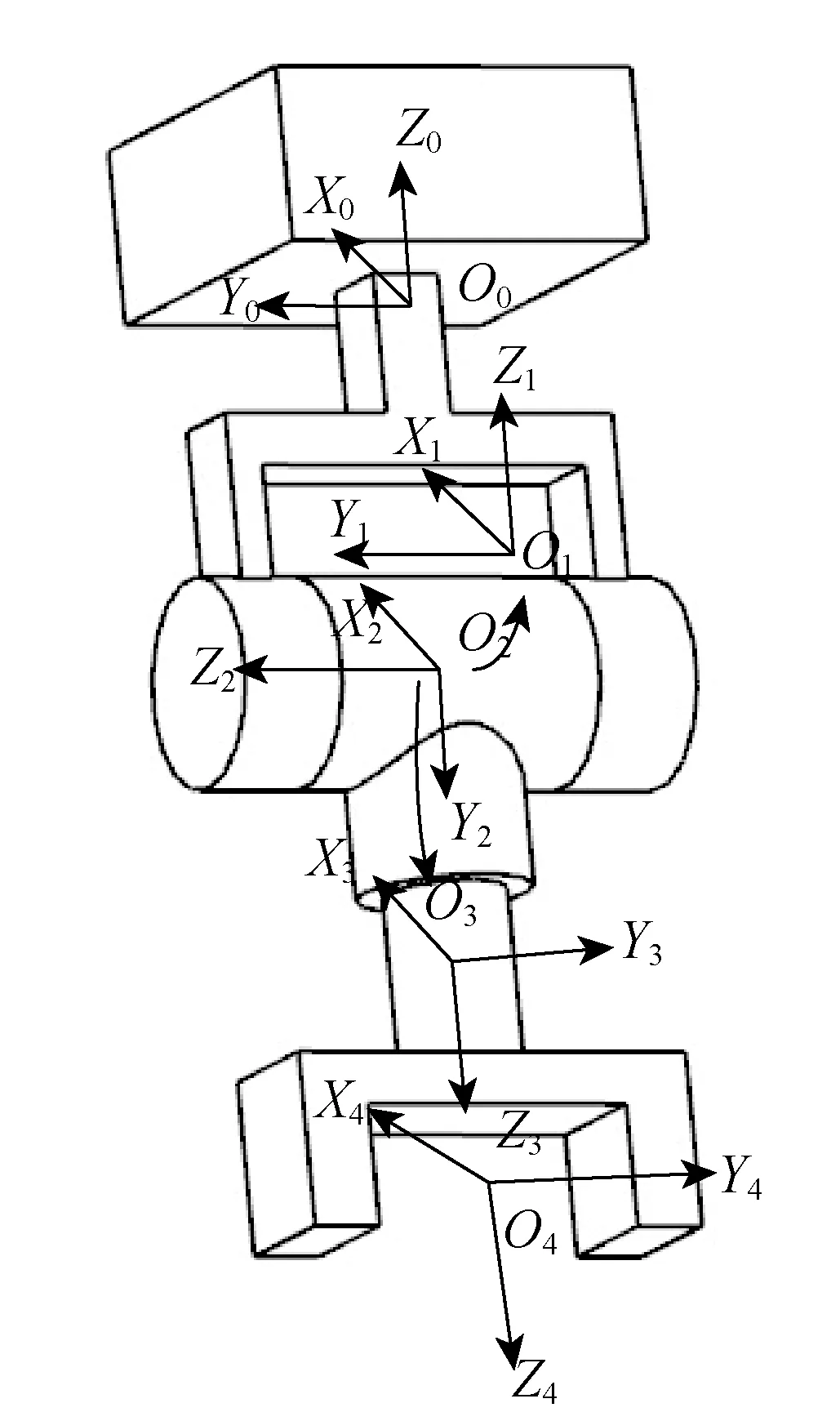
图3 串联模块坐标系分布Fig.3 Coordinates of the serial module表1 D-H法连杆参数表Table 1 Link parameters table utilizing the D-H method

关节iαi-1/(°)ai-1/mmdi/mmθi/(°)2-9000θ23-9000θ3

由D-H坐标参数可以计算出各相邻连杆的齐次变换矩阵为

式中：ci=cosθi，si=sinθi，i=2, 3.

那么，机器人末端相对于并联机构动平台坐标系的变换矩阵，也即串联机构正运动学方程为

(14)

从而得到末端位姿矩阵与两个关节角变量的解析表达式，求得了其运动学正解.

坐标系1相对于参考坐标系(即并联机构动平台上的坐标系)的变换矩阵为

(15)

式中：L4为图3中坐标系原点O0到O1的距离.

坐标系4(混联机构末端坐标系)相对于坐标系3的变换矩阵为

(16)

式中：L5为图3中坐标系原点O3到O4的距离.

所以机构末端相对于动平台的位姿可以表示为

(17)

4.3 自由度混联机构位置分析

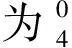
(18)

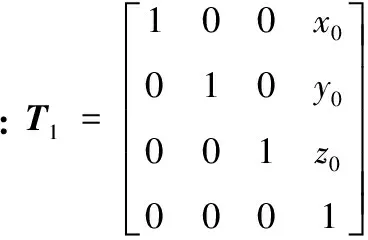
代入式(18)中可得：

则此混联机构的位置方程为

(19)

将式(12)代入式(19)中可以得到：

(20)

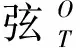
(21)

用欧拉角表示的姿态角度和机构的姿态方程对应起来，则可以得到：

-sin θ2=sin β

(22)

由式(22)可以得到θ2=β+π或者θ2=-β.

(1) 当θ2=β+π时，即cos θ2=-cos β进而代入cos θ2cos θ3=cos βcos γ中，则可得cos θ3=-cos γ，由此θ3=γ+π或者θ3=π-γ.

① 当θ3=γ+π时，则cos θ3=-cos γ，sin θ3=-sin γ，cos θ2=-cos β，sin θ2=-sin β.

由此矩阵

令-cosαcosθ2=-cosθ2，则cos α=1，α=0，sin α=0.

刚好符合旋转变化，则θ2=β+π，θ3=γ+π，α=0.

② 当θ3=π-γ时，则cos θ3=-cos γ，sin θ3=sin γ，cos θ2=-cos β， sin θ2=-sin β.由此，矩阵不满足机构的运动学姿态变化矩阵.

(2) 当θ2=-β时，即cos θ2=cos β.观察式(17)和(21)第1行第1列中cos θ2cos θ3=cos βcos γ，则得cos θ3=cos γ，由此θ3=γ或者θ3=-γ.

① 当θ3=γ时，则cos θ3=cos γ，sin θ3=sin γ，cos θ2=cos β，sin θ2=-sin β.

由此矩阵

刚好符合机构运动学姿态变化矩阵，所以θ2=-β， θ3=γ， α=π.

② 当θ3=-γ时，则cos θ3=cos γ，sin θ3=-sin γ，cos θ2=cos β，sin θ2=-sin β.由此矩阵不满足机构的运动学姿态变化矩阵.

综上所述，θ2=β+π， θ3=γ+π， α=0； θ2=-β， θ3=γ， α=π.

由此可以得到此混联机构姿态的正解：α=0， β=θ2-π， γ=θ3-π； α=π， β=-θ2， γ=θ3.

5 混联机构速度分析

可以用雅可比矩阵来表达并联机构动平台的输出速度和驱动关节的输入速度之间的映射关系，即：

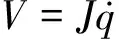
(23)

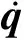
5.1 并联模块速度与加速度分析

将式(13)左右两边同时对时间求一阶导数得：

(24)

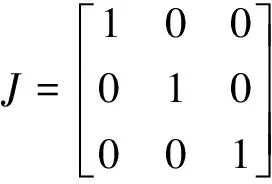
(25)

将式(24)左右两边同时对时间求二阶导数得：

(26)

式(24)和(26)分别表示了并联机构输入、输出之间的速度和加速度关系.

5.2 混联机构速度分析

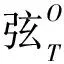
由式(19)可得末端执行器的线速度为

(27)

由式(27)可得：

(28)

此时发现，求雅可比矩阵的关键是保证操作空间和两个串联的关节空间速度一一映射，即将空间的3个姿态表示成关于θ2和θ3的表达式.

当用X-Y-Z欧拉角(α,β,γ)表示动平台姿态时，欧拉角(α,β,γ)对时间的导数在X轴、Y′轴、Z″ 轴上，X、Y′和Z″非正交.将X、Y′和Z″转换到{O}上，则动平台角速度可用欧拉角导数表示为

(29)

当θ2=β+π，θ3=γ+π，α=0时，

则

(30)

则机构的雅可比矩阵为

(31)

当θ2=-β， θ3=γ， α=π时，

则

(32)

则机构的雅可比矩阵为

(33)

由式(31)和(33)可知，两次求得的速度雅可比矩阵相同.

6 混联机构运动性能指标

6.1 混联机构工作空间分析

影响工作空间的因素有杆长的约束、转动副转角的约束、连杆之间的运动干涉.给定并联模块各支链第1个移动副的输入杆长限制为L1，第4个移动副的杆长限制为L3，第2个转动副与第3个转动副连线的转动角度分别为α1、β1、γ1，根据工程实践，限制这3个转动角度范围为0°～180°.串联模块第1个转动副的范围为-90°～90°，第2个转动副的范围为-180°～180°.

设定3-PRRPR +2R机构的尺寸参数：L1min=0 mm，L1max=500 mm，L2=500 mm，L3min=0 mm，L3max=500 mm；D2z=100 mm，D3y=100 mm；L4=120 mm，L5=120 mm.

采用直角坐标系对混联机构的可达工作空间进行搜索，运用蒙特卡洛法对空间可达的点用星号标注，得到该混联机构的可达工作空间如图4所示.

6.2 混联机构的奇异性分析

机构处于奇异位形是指雅可比矩阵的秩比作业向量(或伪作业向量)维数小的位形[16].3-PRRPR +2R 5自由度混联机构的奇异问题可以通过判断速度雅可比矩阵是否满秩来分析[17].由于此雅可比矩阵为一个6×5的矩阵，无法直接通过求雅可比矩阵的行列式的形式来求解其奇异位形.

在本文5自由度混联机械臂的工作空间内遍历计算速度雅可比矩阵J在工作空间内的秩，结果发现不存在秩小于5的情况，可以确定该混联机械臂在工作空间内不存在奇异位形.

利用雅可比矩阵的转置与雅可比矩阵相乘就可以得到一个5×5的矩阵，求此矩阵的行列式的值为1，所以此混联机构具有各向同性.

7 结 论

(1) 本文提出的5自由度混联机构结构简单，并联模块采用3个移动副驱动可实现三维移动，承载能力强，串联模块采用两个转动副驱动实现二维转动，整个机构结构紧凑.通过判断并联模块的消极副，简化了机构，串联模块采用D-H方法求得运动学变换矩阵，从而推导了整个混联机构的位置正反解和速度，验证了机构运动解耦特性，以方便实时控制.

(2) 运用速度传递形式，将并联模块得到的三维移动参数转化成D-H参数，得到整个混联机构的运动姿态表达式，使其与用欧拉角表示的末端姿态相等，得到欧拉角与输入参数之间的关系，从而推导了混联机构的雅可比矩阵，验证了机构具有完全各向同性.

(3) 混联机构的工作空间是一个长方体，工作空间体积大，机构不存在奇异，具有很好的运动学性能和灵活性，因此具有很好的应用价值.

[1] YANG D, LI T J, LIU J Y, et al. Research on the pose detection and control methods of robot with series-parallel structure[J]. Applied Mechanics and Materials, 2013, 303/304/305/306: 16851690.

[2] LU Y, HU B. Solving driving forces of 2(3SPR) serial-parallel manipulator by CAD variation geometry approach[J]. Journal of Mechanical Design, 2006, 128(6):13491351.

[3] 姜铭,孙钊,秦康生,等. 混联机器人的分析与研究[J].制造业自动化,2009,31(1):6165.

[4] 黄玉美,高峰,史文浩.混联式数控机床的发展[J].制造技术与机床,2001(8):89.

[5] 王艳,孟祥志.三杆混联数控机床的运动学研究[J].中国机械工程,2005,16(15):13211324.

[6] 高云峰,吕明睿,周伦,等.一种五自由度混联机器人运动学分析[J]. 哈尔滨工业大学学报, 2014, 46(7):17.

[7] 杜玉湘,陆启建,刘明灯,等.五轴联动数控机床的结构和应用[J].机械制造与自动化,2008,37(3):1416,20.

[8] 李菊,赵德安,沈惠平,等.多喷枪协同式喷涂五轴混联机器人设计[J].农业机械学报,2012,43(4):216220.

[9] PISLA D, SZILAGHYI A, VAIDA C, et al. Kinematics and workspace modeling of a new hybrid robot used in minimally invasive surgery[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(2):463474.

[10] HUANG T, LI M, ZHAO X M, et al. Conceptual design and dimensional synthesis for a 3-DOF module of the TriVariant-a novel 5-DOF reconfigurable hybrid robot[J]. Robotics IEEE Transactions on, 2005, 21(3):449456.

[11] ZHANG D, ZHANG F. Design and analysis of a totally decoupled 3-DOF spherical parallel manipulator[J]. Robotica, 2011, 29(6):10931100.

[12] HUANG Z, LIU J F, ZENG D X. A general methodology for mobility analysis of mechanisms based on constraint screw theory[J]. Science in China, 2009, 52(5):13371347.

[13] 王英,李秦川,武传宇,等. 一种具有各向同性的3-PPRRR移动并联机构[J]. 中国机械工程,2009,20(10):11351140.

[14] 高振.空间三自由度并联/混联机构构型、性能与若干应用研究[D].合肥：中国科学技术大学信息科学技术学院,2009.

[15] 崔培.3-RPS+RP五自由度混联机械臂机构学分析与仿真研究[D].秦皇岛：燕山大学机械工程学院, 2011.

[16] 万海波.五自由度机械手运动性能及动力学分析与仿真[D].天津：河北工业大学机械工程学院,2007.

[17] REZAEI A, AKBARZADEH A. Study on Jacobian, singularity and kinematics sensitivity of the FUM 3-PSP parallel manipulator[J]. Mechanism & Machine Theory, 2015, 86(2): 211234.

Kinematic and Performance Analysis of 3T2R Hybrid Mechanism

CAOHao-feng1,2,3,CAOYi1,2,4,CHENHai1,2,QINYou-lei1,2,DINGRui1,2

(1. School of Mechanical Engineering, Jiangnan University, Wuxi 214122, China;2. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Wuxi 214122, China;3. Ningbo Radio & TV Vnivresity, Ningbo 315000, China;4. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiaotong University, Shanghai 200240, China)

The 5-DOF(degree of freedom) hybrid mechanism is composed of a fully-isotropic three-dimensional translational parallel mechanism and a 2 DOF rotational serial mechanism. The position of the end-effector for the hybrid mechanism depends on the two parts, while the orientation is completely determined by the serial part. First of all, the number of degrees of freedom of the mechanism is calculated, and its characteristic is analyzed based on screw theory. Then, the driven pair of the mechanism is selected and further research shows that the fifth revolute pair in each limb of the parallel mechanism is inactive, these pave theoretical grounds for the following analyses. Finally, the kinematical characteristics of the hybrid mechanism are analyzed by deriving its velocity Jacobian matrix based on kinematic influence coefficient and analyzing its workspace and singularity. The hybrid mechanism has a good application prospect owing to its kinematics decoupling, the large workspace and singularity-free characteristics.

hybrid mechanisms; screw theory; kinematics; workspace; singularity

16710444 (2016)060881-08

20150909

国家自然科学基金资助项目(50905075)；机械系统与振动国家重点实验室开放课题资助项目(MSV201407)；江苏省食品先进制造装备技术重点实验室开放课题资助项目(FM-201402)

曹浩峰(1990—)，男，浙江宁波人，硕士研究生，研究方向为混联机器人机构学理论及机器人技术.E-mail：haofeng_cao@163.com 曹 毅(联系人)，男，副教授，E-mail：caoyi@jiangnan.edu.cn

TH 112

A