回归测试路径优先级模型

杜庆峰， 冯国尧， 钱浩然

(同济大学 软件学院，上海 201804)

回归测试路径优先级模型

杜庆峰， 冯国尧， 钱浩然

(同济大学 软件学院，上海 201804)

为了提高回归测试的效率，根据组件间的调用图，找出可能的路径片段，通过测试用例的执行历史进而计算出路径片段的覆盖指数，最后对覆盖指数进行排序，提出了一种测试用例的优先级模型.用此模型可以高效地进行回归测试，及时发现程序中的错误.

回归测试； 路径片段； 优先级模型； 覆盖指标

随着信息技术的迅猛发展，软件已经被应用于各个领域,同时软件的竞争也日益激烈,保证软件的质量就变得尤为重要.软件测试作为软件质量的可靠保障，在软件的整个生命周期中占有越来越重要的地位.软件的调试、升级与维护往往需要更改部分代码，为了验证修改后的程序是否引发新的问题或对未修改的部分是否造成影响，就需要频繁地对软件进行回归测试.

回归测试可以发生在软件测试的任何一个级别，由于在软件测试中随着软件组件的增加、组件的修改或组件的删除需要对其做大量的回归测试.回归测试可以使用之前的测试用例集，也可以针对具体情形对新增的功能编写新的测试用例，删除部分冗余的测试用例.那么，如何提高测试用例的使用效率、如何优先使用以往的测试用例是测试用例优先级技术的关注重点.测试用例优先级技术认为不同测试用例对于测试目标的完成有着不同的贡献程度，为了能够更快地达成测试目标，有必要将不同的测试用例进行比较和排序，然后优先执行相对重要的测试用例.

Wong等[1]最先提出了在回归测试选择技术的基础上对测试用例集进行最小化或优先级处理，通过判定累计覆盖率等问题对测试用例进行排序.在此之后，越来越多的学者将测试用例的优先级技术运用到回归测试当中.Kim等[2]研究了综合考虑各种测试历史的优先级技术.Jeffrey等[3]研究了基于切片的测试用例优先级技术.

因此，针对如何选择和使用测试用例，应该结合该测试用例的历史覆盖情况设定其优先级,从而缩短测试的时间，减少所产生的开销.

1 问题提出

Rothermel等[4]将测试用例优先级问题抽象为寻找测试用例全排列中的最优集合问题.给定测试用例集T，T的全排列集合PT，从PT到实数的函数f，求一个T′∈PT，使得∀T″,T″∈PT且T″≠T′且f(T′)≥f(T″) .换句话说,如果一组测试用例按照特定的顺序执行,那么该组测试用例使得目标函数f有更高的“适宜度”值.一般认为,更高的适宜度值代表更好的测试用例优先级排序.

在理想情况下,测试用例应该尽可能早地最大化错误检测能力(即，提高错误检测的速率),因此，优化测试用例集，通过调整测试用例顺序[5]，可以最大化提高错误检测能力以便更早地向程序员提供反馈信息，从而使他们更早地定位和修复错误.

例如，某被测程序中测试用例和对应的检错情况如表1所示,表示测试用例t是否覆盖了程序缺陷f,其中“√”表示t覆盖了f.在回归测试中如果按照t1～t7的顺序执行,那么直到执行测试用例t3的时候才能检测到第1个错误，同时只有执行到t7的时候才能检测到所有的错误缺陷.如果根据t3，t4，t5，t7,t6，t1，t2的执行顺序执行测试用例，那么就能更快地发现程序中的错误，同时能更快地检测出所有的错误，这能大大减少测试成本.

表1 测试用例检错表示例Tab.1 Error detection table of test case

在现阶段，回归测试时主要是根据需求手动选取测试用例顺序，其效率比较低下;或者是仅仅根据测试用例对路径的覆盖率来决定测试用例的优先级，其严谨性有待考量.针对以上的不足，在进行路径片段覆盖指数分析的基础上,研究测试用例优先级的模型.

综上，若构建一个基于路径片段覆盖指数的优先级模型，需解决以下的问题：①对于路径片段和测试用例的关系进行分析，并得出各个路径片段的详细历史覆盖信息.②根据路径片段的历史覆盖信息，得出各个路径片段的覆盖指数，生成路径片段的递减集，并分析递减集和测试用例优先级模型的关系.

2 回归测试优先级模型

2.1 相关定义

回归测试优先级模型主要是对组件调用路径进行分析，组件调用路径中包含函数结点(也称之为组件结点)和路径片段.通过分析路径片段的覆盖指数，进一步得出相关测试用例的优先级.为了方便对函数调用路径和对路径片段的覆盖进行分析，现作定义如下.

定义1 组件调用路径图.假设在软件测试中每一个组件是一个结点，对于组件之间相互的调用，可以得到一个从程序入口结点到出口结点的有向调用图,可以表示为P={N1,N2,…,Ni,…,Nn}，其中Ni为组件结点.Ni和Ni+1的相邻关系表示Ni+1调用了Ni，则称P为组件调用路径图.图1表示从结点1开始到结点9结束的组件调用路径图.

图1 组件调用路径示例Fig.1 Example of component call path diagram

定义2 路径片段和路径片段集.假设在组件的调用路径图中，若组件结点Ni到结点Nj存在一条连通的路径，则这条路径称为Ni到Nj的路径片段，路径片段中结点数目不定.组件调用路径图中的所有路径片段构成路径片段集,可以表示为Sm={s1,s2,…,si,…,sm},其中Sm为路径片段集，si为路径片段.

定义3 路径片段覆盖指数.在执行一个测试用例集后，每一个测试用例可能会覆盖若干个路径片段，同时一个路径片段也可能被若干测试用例覆盖，假设si为其中一个路径片段，那么覆盖si所对应的测试用例数目之和称为si的覆盖指数，记为Ci,m，其中i表示第i个路径片段，m为所有的路径片段数目.

定义4 路径片段递减集.假设在执行测试用例集之后，根据路径片段的覆盖指数大小得出一个路径片段集合Sd={sd1,sd2,…,sdi,…,sdm},其满足Cd1,m>Cd2,m>…>Cdm,m，则称为路径片段递减集.

2.2 优先级模型构建

2.2.1 模型理论

回归测试路径优先级模型是将功能看成一个组件结点的形式.根据组件结点之间的相互调用关系，将各个组件进行集成，得到组件调用路径图.图1就是一个组件调用路径图.

在组件的调用路径图中，结点之间的连通形成很多路径片段，其中每条路径片段包含若干结点.例如图1中结点2，5，7就构成了1个3个结点的路径片段.通过执行历史测试用例集，进而可分析各路径片段的覆盖指数,其中路径片段和测试用例满足二元关系(如表2)可表示G(T,S)nm矩阵形式.

表2 测试用例集和路径片段满足的二元关系实例Tab.2 Examples of binary relations between test suite and path segments

该模型根据组件调用路径图，结合图论思想，遍历出路径片段的数目.根据测试用例集和路径片段的关系，计算出每个路径片段的覆盖指数.对所有路径片段的覆盖指数进行比较，得出一个路径片段递减集.通过分析路径片段递减集中覆盖指数高的路径片段所对应的测试用例得出测试用例的优先级模型,同时在之后的回归测试中采用动态调整策略研究补充测试用例的优先级模型.对路径片段覆盖指数低的测试用例适当删除，同时添加覆盖指数高的测试用例，以不断完善模型.

2.2.2 模型的数学表达

在进行回归测试之前，需要满足执行完测试用例集时，组件调用路径图中的所有路径片段都是被覆盖的，即要求覆盖程序中所有可能的路径[6].这样以确保测试用例集是完整的、有效的.

假设测试用例集为T={t1,t2,…,tn}，路径片段集是S={s1,s2,…,sm}，在回归测试之前对于每个sj∈S，在T中至少有一个测试用例ti能够覆盖sj.同时测试用例集T与路径片段集S满足二元关系，用符号可表示为矩阵G(T,S)nm.假设测试用例ti能覆盖路径片段sj(1≤i≤n,1≤j≤m)，则G(ti,sj)=1,否则G(ti,sj)=0.当∃ti使S中的任意一个路径片段sj使得G(ti,sj)=1,i∈[1,n],则此测试用例集是有效的.

假设实际中的路径片段为m个,那么路径片段sj(1≤j≤m)的覆盖指数可以表示为Cj,m,其中路径片段和测试用例满足二元关系G(T,S)nm=(gij).

此矩阵的C1,m=2,C2,m=3,C3,m=1,…,Cm,m=1.

在根据以上矩阵G(T,S)nm得出每一个路径片段的Ci,m值时，对所有路径片段Ci,m值进行排序和统计，得出一个Ci,m递减的路径片段集合.那么在回归测试中，需要优先对Ci,m值高的路径片段设计测试用例或者从已有的测试用例集中选取Ci,m值高的路径片段的对应测试用例，提高其优先级别.假设一个路径片段递减集合是{s2,s3,s1,s4}，那么优先赋予s2更高的优先级，那么覆盖s2的测试用例对应的级别较高；假设覆盖s2的测试用例有若干条，那么需要比较这些测试用例是否覆盖其他高覆盖指数的路径片段，若一条测试t1用例除了覆盖s2还覆盖了一个s3，而另一个测试用例t2覆盖了s2和s1，则t1测试用例优先级高于t2.

在路径片段递减集合中存在相同覆盖指数的路径片段si，sj，若si∈sj，则有效路径片段为sij=si∪sj=sj.若si∉sj，则需分析覆盖si，sj的测试用例是否覆盖其他路径片段，依次比较覆盖指数，确定优先级.若2个测试用例覆盖的所有片段的覆盖指数都是相同的，此时需要确定最高覆盖指数路径片段的si和sj组件数目.比如si(n1,n2,…,nx),sj(n1,n2,…,ny)，若x>y，则表示si片段对程序的贡献大，因此相应的优先级较高.

3 模型算法及验证

3.1 算法思想

(1) 根据分析相关程序的集成，确定程序中组件的个数，进而分析函数组件之间的调用关系，生成组件调用路径图.假设组件调用路径图中有m个组件，根据组件的个数以及特定的逻辑调用关系得出该组件调用图中的实际路径片段.

(3) 根据以上二维数组可以得出每一个路径片段的Ci,m值，对所有路径片段Ci,m值进行排序和统计，得出一个Ci,m递减的路径片段集合.在回归测试中，优先对Ci,m值高的路径片段设计测试用例或者从已有的测试用例集中选取Ci,m值高的路径片段的对应测试用例，提高其优先级别.

(4) 对排序好后的路径片段进行分析.排序后Ci,m值高的路径片段表示被T覆盖的次数多,因此在进行回归测试的时候，赋予覆盖该路径片段的测试用例更高的优先级.这样便能在很短的时间内优先测试出函数间的关键路径.当Ci,m值相同的时候，存在以下情况：

若路径片段si和路径片段sj对应的覆盖指数相同，且si是sj的子片段，那么有效的路径片段为sj.在该情况下只需要考虑路径片段sj的情况，而无需再考虑路径片段si的情况.

若路径片段si和路径片段sj对应的覆盖指数相同，但是si不是sj的子片段，那么需要对覆盖该路径片段的若干测试用例进行进一步比较.假设C4,m=C7,m=10，那么就需要对覆盖s4,s7片段的测试用例进行比较.假设有10条测试用例覆盖s4,s7,则比较这10条测试用例是否覆盖其他Ci,m值高(比10略低)的片段，按照这10条测试用例对其他路径片段的覆盖情况，对应Ci,m值高的测试用例优先级高.最后如果2条测试用例覆盖的所有片段的覆盖指数都是相同的，那么需要确定最高路径片段的组件数目，组件数目多则对程序的贡献大，因此相应的优先级较高.

3.2 算法逻辑

为了验证以上模型算法，将伪代码整理如下.

Procedure Test-case

Input :T, Integrated program

Output: T of the high priority

Begin

generate component call path graph

get the segment path from component call path graph

build a matrixG(T,S)n*m

if T coversi

A[i][j]=1

else

A[i][j]=0 /*storage relationship between test cases and path segments*/

calculate the number of ‘1’ in the matrix column namedCi,m

sortCi,mvalue

ifCi,mis the max

give thetihigher priority

else ifCi,m=Cj,m

Ifsi∪sj=sj

just concernsj

else

for(i=n,j=n;i>0,j>0;i--,j--)

ifCi,m>Cj,m

give thetihigher priority thantj

else ifCi,m=Cj,m

compare the n number of thesiandsj

ifni>nj

give thetihigher priority thantj

all T have priority and put it into a list

End

3.3 算法复杂度分析

3.3.1 时间复杂度

3.3.2 空间复杂度

根据组件调用路径图中所得的路径片段的空间复杂度为O(n)构造矩阵的空间复杂度为O(n2)，排序空间复杂度为O(1)，故此模型的空间复杂度为：O(n)+O(n2)≈O(n2).

3.4 算法验证

3.4.1 优先级模型的测评标准

软件测试的目的是设计出高质量的测试用例来尽可能多地检测出被测软件内部存在的缺陷.在设计测试用例优先级的评测指标时，需要体现出测试用例的缺陷检测速率.

APFD[7-9]为缺陷检测加权平均百分比.假设测试用例集T中包含n个测试用例，该测试用例集合能够检测出的错误集合为F，其中F包含m个错误，则测试用例集T的一个顺序集T′的APFD值可以用如下公式表达：

式中:Ri为顺序集T′中第1个检测出错误i的测试用例在T中的位置.∂APFD的取值范围在0～1之间.在不同的测试用例顺序集中，∂APFD越高表示对应测试用例优先级集的检测错误的效率相对越高.

例如测试用例检测表如表1所示,那么若按照t1～t7的顺序执行测试用例，则该执行顺序集的∂APFD为

若根据t3，t4，t5，t7,t6，t1，t2的顺序执行,那么该执行顺序的∂APFD为

由以上可知，按照上述测试用例的优先级顺序执行测试可以提高错误的检测效率.

3.4.2 试验设计与分析

试验采用的测试工具是selenium IDE软件.通过搭建selenium测试环境进行相关测试.本次试验的数据是时态GIS(Geographic Information System)系统中的部分数据.首先根据项目画出组件调用路径图.其结果如图2所示.

图2 组件调用路径Fig.2 Component call path diagram

通过图论的遍历可知不重复的有效路径片段数目是33条.在该试验中，设计了10条测试用例.测试项编号为SVG_TC_001.该测试用例表中的测试用例覆盖了全部路径，同时对重点功能设计相应多的测试用例，用以满足测试用例的设计条件.执行完所有测试用例之后，经过算法分析统计可知：0→3路径片段被测试用例覆盖了8次，为最高覆盖指数的路径片段，0→3→5 和3→5的路径片段覆盖指数为4次，但是根据算法sij=si∪sj=sj可知，只需要考虑0→3→5的路径片段覆盖指数，而无需再考虑路径3→5的覆盖指数.同理0→3→4→9，0→3→4，3→4，3→4→9，4→9路径片段覆盖指数都为3次，其只需考虑0→3→4→9的覆盖指数.根据算法依次可知0→3→5→8→9的路径片段覆盖指数为3次，0→1→2→9的覆盖指数为2次，0→3→6→9和0→3→5→7→9的覆盖指数为1次.测试发现编辑地图和比对地图2个功能模块存在缺陷.然后对该项目添加若干功能进行相关回归测试.在对项目进行相关修改后的组件调用图如图3所示.

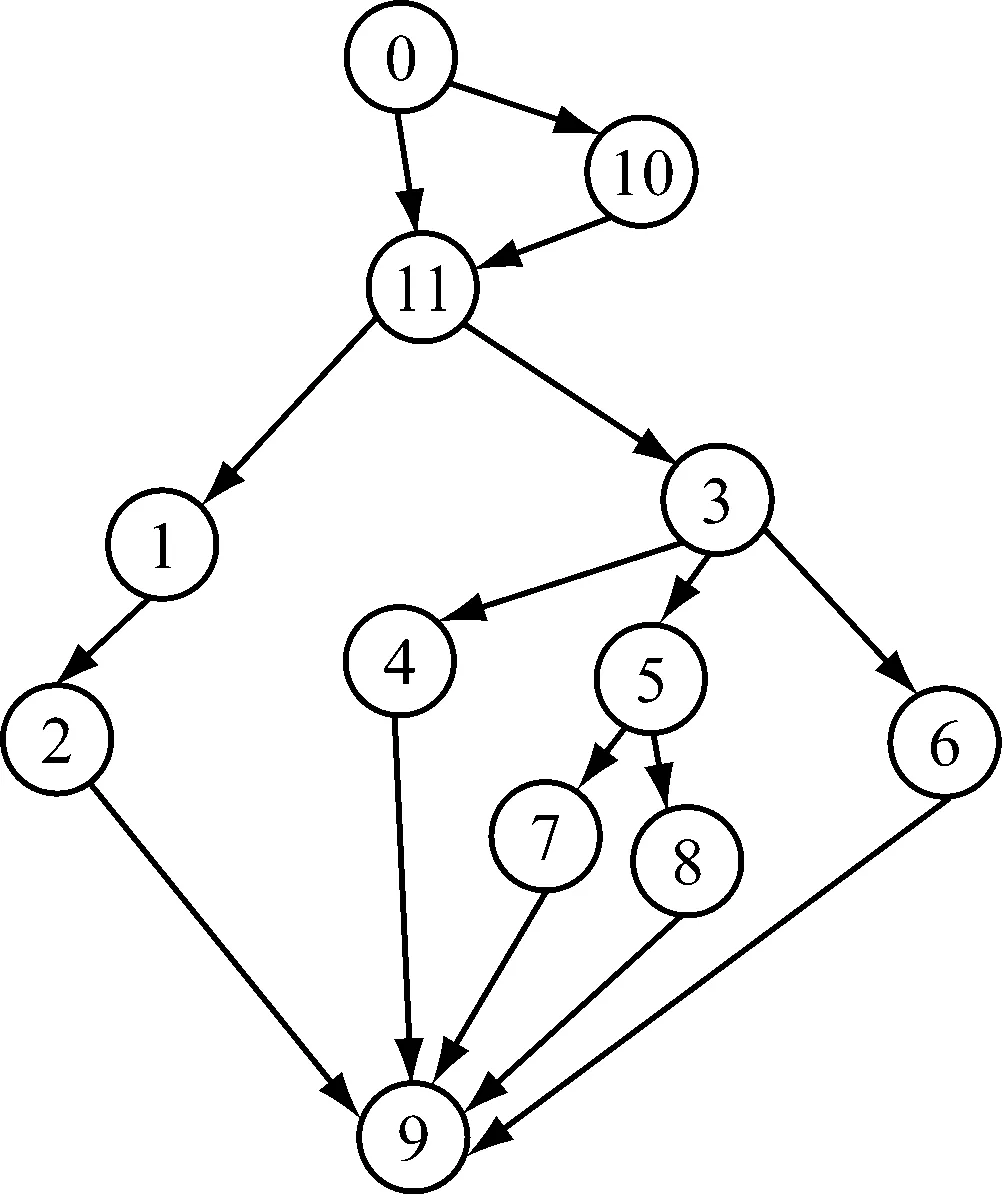
图3 修改后的组件调用路径Fig.3 Modified component call path diagram

根据回归测试路径优先级算法模型可知：路径0→3→5→8→9对应的测试用例是优先级最高的测试用例，因此在对修改后的项目组件调用图进行回归测试时应该根据0→3→5→8→9对应的测试用例做部分修改，然后优先进行测试.因此在回归测试中应该优先使用0→10→11→3→5→8→9 和0→11→3→5→8→9路径所对应的测试用例.同理其次的测试顺序应该依照算法得出的回归测试优先级从高到低的顺序进行选取.依次进行测试后可以得出表3.

表3 测试用例检错表Tab.3 Error table of test case

由此可得初始阶段的∂APFD为0.2，新阶段的∂APFD为0.6.因此在进行回归测试时使用测试用例优先级选取的测试用例可以大大提高检错效率.

3.4.3 试验结果

在回归测试中，测试用例优先级技术旨在找到一种高效的测试用例执行序列，按照测试用例序列的执行顺序进行测试能提高错误的检错效率.表4是对其他5组程序进行试验得出的数据，能充分反映优先级模型的检错效率.其中数据来源于缺陷测试项目组和时态GIS系统.

图4是表4反映的初始的∂APFD和排序后∂APFD的对比图，能直观反映在执行模型算法前后缺陷检测加权平均百分比的变化.

图4 模型执行前后APFD值对比Fig.4 APFD comparison chart before and after model execution

通过试验分析可知：使用路径优先级模型排序后的测试用例的APFD值要高于未排序测试用例的APFD值，且两者有较大的差值，说明了提出的测试用例优先级模型能明显提高测试的缺陷的检错效率;同时随着软件规模的增加，测试用例优先级模型的缺陷检测率提升也愈发稳定.

4 结语

传统的基于覆盖的优先级技术是根据每条测试用例的覆盖率进行排序然后来设定其测试用例的优先级，而本文是根据若干测试用例所对应的每一条路径片段的覆盖指数确定重点需要测试的路径片段，再根据此路径片段反过来寻找对应的测试用例，进而赋予其对应的优先级.

由于该优先级模型是根据路径覆盖指数生成的，故能更好地反映测试用例的执行记录，从而发现系统中重点测试片段.其对应的测试用例执行顺序能明显地提高项目回归测试的效率.

[1] Wong W E, Horgan J R, London S,etal. A study of effective regression testing in practice[C]∥The Eighth International Symposium on Software Reliability Engineering.[S.l.]: IEEE Computer Society, 1997:264-274.

[2] Kim J M, Porter A. A history-based test prioritization technique for regression testing in resource constrained environments[C]∥International Conference on Software Engineering. New York:[s.n.], 2002:119-129.

[3] Jeffrey D, Gupta N. Test case prioritization using relevant slices[C]∥30th Annual International Computer Software and Applications Conference[S.l.]: IEEE, 2006: 411-420.

[4] Rothermel G, Untch R H, Chu C,etal. Prioritizing test cases for regression testing[J]. Acm Sigsoft Software Engineering Notes, 2000, 25(5):102.

[5] 安金霞，王国庆，李树芳，等.基于多维度覆盖率的软件测试动态评价方法[J].软件学报，2010,21(9):2135.

AN Jinxia, WANG Guoqing, LI Shufang,etal.Dynamic evaluation method based multi-dimensional test coverage for software testing[J].Journal of Software,2010,21(9):2135.

[6] 杜庆峰. 高级软件测试技术[M].北京：清华大学出版社，2011.

DU Qingfeng.Advanced software testing techology[M].Beijing:Tsinghua University Press,2011.

[7] 李华莹，胡兢玉.回归测试用例优先级排序技术研究[J].计算机仿真，2013,30(10):298.

LI Huaying, HU Jingyu.Research on test case prioritization for regression testing[J].Computerised Simulation, 2013,30(10):298.

[8] 陈翔，陈继红，鞠小林，等.回归测试中测试用例优先排序技术述评[J].软件学报，2013,24(8):1695.

CHEN Xiang,CHEN Jihong,JU Xiaolin,etal.Survey of test case prioritization techniques for regression testing[J]. Journal of Software, 2013,24(8):1695.

[9] 牟永敏，李慧丽.基于函数调用路径的测试用例优先级排序[J].计算机工程，2014,40(7):243.

MOU Yongmin, LI Huili. Test case prioritization based on function calling paths[J]. Computer Engineering, 2014,40(7):243.

Path Priority Model of Regression Testing

DUQingfeng,FENGGuoyao,QIANHaoran

(School of Software Engineering, Tongji University, Shanghai 201804, China)

In order to improve the efficiency of regression testing, test case prioritization technology is particularly important. This paper is mainly to identify possible path segments by the call graph between components, to calculate path segments’ cover index by the execution history of test cases, and finally to put forward a priority model of test case based on the sort of the cover index.Through the research of this model, it can effectively carry out regression test, and detect the errors in the program timely.

regression testing; path segment; priority model; coverage index

2015-10-15

国家自然科学基金(41171303)

杜庆峰(1968—)，男，教授，博士生导师，工学博士，主要研究方向为软件测试、计算机相关学科交叉领域. E-mail： du_cloud@tongji.edu.cn

TP311.5

A