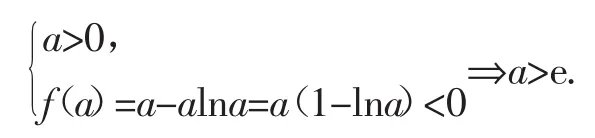转化消元尽显数学之神韵

☉湖北省襄阳市第五中学 曹标平

转化消元尽显数学之神韵

☉湖北省襄阳市第五中学 曹标平

我们在解决数学问题时，常把复杂、生疏、抽象、困难、未知的问题变成简单、熟悉、具体、容易、已知的问题来解决，这是一种思想方法，也是一种策略.若再能从题目的本身特征出发，灵活巧妙运用消元法，不仅可以简化解题过程，而且有利于培养思维能力.

本文以2016年新课标Ⅰ卷理数压轴题及其一些变式题为例，让我们一起好好体会把“未知”转化为“已知”、复杂问题转化为简单问题的基本数学思想方法在导数类压轴题中的应用.

例1（2016年新课标Ⅰ卷理科）已知函数f（x）=（x-2）ex+a（x-1）2有两个零点.

（1）求a的取值范围；

（2）设x1，x2是f（x）的两个零点，证明：x1+x2＜2.

解析：（1）略.

（2）不妨设x1＜x2，由（1）知x1∈（-∞，1），x2∈（1，+∞），2-x2∈（-∞，1）.

f（x）在（-∞，1）上单调递减，所以x1+x2＜2等价于f（x1）＞f（2-x2）.

即证f（2-x2）＜0.

由于f（2-x2）=-x2e2-x2+a（x2-1）2，而f（x2）=（x2-2）ex2+ a（x2-1）2=0，所以f（2-x2）=-x2e2-x2 -（x2-2）ex2

.

设g（x）=-xe2-x-（x-2）ex，则g′（x）=（x-1）（e2-x-ex）.

所以，当x＞1时，g′（x）=0.

而g（1）=0，故当x＞1时，g（x）＜0.

从而g（x2）=f（2-x2）＜0，故x1+x2＜2.

点评：本题转化思想主要体现在两点：①x1，x2本不在f（x）的同一个单调区间内，但通过移项使得x1和2-x2在f（x）的同一个单调减区间内；②要证明x1，x2间的关系，利用分析法转化为证明函数值间的不等关系.本题消元法主要体现在利用f（x1）=0直接消去x1和利用f（x2）=0消去参数a.

例2已知f（x）=在x=-1处的切线方程为ex-y+ e=0.

（1）求实数a，b的值；

（2）若存在不相等的实数x1，x2，使得f（x1）=f（x2），求证：x1+x2>0.

解析：（1）由

所以f（x）在（-∞，0）上单调递增，在（0，+∞）上单调递减，且f（0）=1>0.

不妨设x1<00.

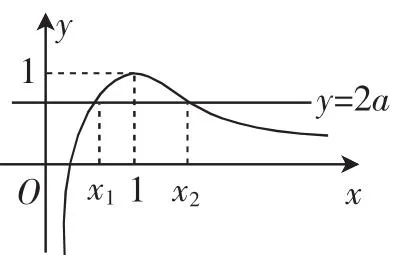
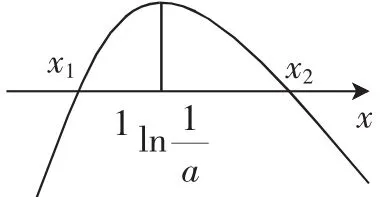
要证x1+x2>0⇐x2>-x1⇐f（x2）

只需证明g（x）<0即可.

g（x）=（x+1）e-x+（x-1）ex（x<0），g′（x）=x（ex-e-x）>0，所以g（x）在（-∞，0）上单调递增，所以g（x）

点评：本题是通过移项的方法将不在同一个单调区间内的两个数转化到同一个单调区间内来研究，另外直接利用题中条件f（x1）=f（x2）消去x2.

例3已知函数f（x）=x-alnx，a∈R.

（1）研究f（x）在定义域上的单调性.

（2）设函数f（x）有两个不同的零点x1，x2，且x1

①求a的取值范围；

②求证：x1·x2>e2.

解析：（1）x∈（0，+∞），f′（x）=1-

当a≤0时，f′（x）>0，所以f（x）在（0，+∞）上单调递增；

当a>0时，f（x）在（0，a）上单调递减，在（a，+∞）上单调递增.

（2）①因为f（x）有两个不同的零点，由（1）知：

②由①知0

要证x1·x2>e2⇐lnx1+lnx2>2⇐>2⇐x1+x2>2a⇐ x2>2a-x1⇐f（x2）>f（2a-x1）⇐f（x1）>f（2a-x1）⇐f（x1）-f（2ax1）>0.

设g（x）=f（x）-f（2a-x），x∈（0，a），只需证明g（x）<0即可.所以g（x）在（0，a）上单调递减.

所以g（x）>g（a）=0，得证.

点评：首先通过取对数，将乘积问题转化成和的问题，再通过等价转换将对数问题转化成我们熟悉的一次多项式问题，最后利用例3的方法完成本题.需要注意的是本题对x2的处理很有讲究，如果像例1那样利用f（x2）=0消去参数x2，那么后面的数据处理会带来很多麻烦.由于数学试题的多样性和灵活性，我们要合理地设计好转化的途径和方法，避免死搬硬套题型.

例4 已知函数f（x）=xlnx-ax2，若函数f（x）有两个极值点x1，x2（x1

证明：因为函数f（x）有两个极值点x1，x2，所以f′（x）= lnx-2ax+1=0有两个不等的实根，所以即直线y=2a与函数g（x）=的图像有两个不同的交点.

所以g（x）的图像如图1所示，而直线y=2a与函数g（x）=的图像有两个不同的交点，所以2a∈（0，1），即a∈且

图1

所以（fx1）=x1lnx1-=x1lnx1-·x21=< 0.

点评：本题通过分离参数的方法将函数零点问题转化成直线与函数图像交点问题，进而求出a和x1的范围，再利用代入消元的方法就可以直接消去参数a.

例5设f（x）=

（1）求f（x）的单调区间；

（2）若存在x1，x（2x1

解析：（1）略.

所以x1<1

图2

消元的目的是：减少变量的个数，简化形式，便于计算，在应用过程中，体现一种整体思想和转化思想.学习和掌握消元法，不但对巩固基础知识、提高解题能力有重要作用，而且能为进一步学习高等数学提供帮助.中学阶段常用的消元法有代入消元法、加减消元法、放缩消元法等.

著名的数学家、莫斯科大学教授C.A.雅洁卡娅曾在一次向数学奥林匹克参赛者发表《什么叫解题》的演讲时提出：“解题就是把要解题转化为已经解过的题.”数学的解题过程，就是从未知向已知、从复杂到简单的化归转换过程.

在数学操作中实施转化时，我们要遵循熟悉化、简单化、直观化、标准化的原则，即把我们遇到的问题，通过转化变成我们比较熟悉的问题来处理；或者将较为烦琐、复杂的问题，变成比较简单的问题；或者比较难以解决、比较抽象的问题，转化为比较直观的问题，以便准确把握问题的求解过程，比如数形结合法.按照这些原则进行数学操作，转化过程省时省力，犹如顺水推舟，经常渗透等价转化思想，可以提高解题的水平和能力.