消除差异——治愈“三角疑难”症的良方——从近几年江苏高考几道三角压轴题想到的

☉江苏省太湖高级中学 张 敏 侯 斌

·江苏省无锡市王华民名师工作室·

消除差异
——治愈“三角疑难”症的良方——从近几年江苏高考几道三角压轴题想到的

☉江苏省太湖高级中学 张 敏 侯 斌

“继承与创新”历来是高考命题的指导思想，江苏数学高考从2013年以来，以继承、稳定为主，总体难度控制得比较好，其中近四年的填空压轴题（第13、14题），大多是三角、向量试题，而以往这类“高大上”试题只能出现在函数、数列、不等式内容中，这个变化点也是江苏高考试卷的一个创新点.但作为压轴题，难度自然不低，有的思维要求高，有的信息量大，不少学生不知如何入手.解题差异论认为，解题的过程就是消除条件与条件、条件与结论之间差异的过程，要消除整体与局部、数与形的差异，消除多与少、高与低的差异等，它的理论基础是哲学中的对立统一规律及反馈原理.［1］

本文透过几道高考三角填空压轴题，结合笔者多年的教学实践，觉得“消除差异”可以有效解决三角中的一些重、难点问题.在三角问题中消除差异，既要消除条件与目标之间的差异，也要消除条件中不同角、不同（函数）名、不同次数的差异.通过消除差异，以便快速寻求解题突破口，帮助学生释疑解惑，重拾信心.

一、通过三角函数的“名变换”和“角变换”，消除差异

现行高中教材中，三角函数的名称有正弦、余弦和正切，对于求值、化简等问题中同时含有“弦”和“切”的问题，一般是“切”化“弦”，有时需要“弦”化“切”，称为函数“名变换”，以此来消除函数名的差异，再利用“弦”之间或“切”之间的关系求解.如果一个三角函数问题含有几种不同的角，那么解题时就需要寻求它们之间的联系，进行“角变换”，以消除“角”的差异.

例1（无锡市高二数学期末检测题）不查表求值：4sin20°+tan20°.

简析：该题有正弦和正切两个三角函数名，消除函数名的差异，一般通过“切”化“弦”，4sin20°+再通分、整理，得因有两个20°角和1个40°角，需要消除差异角40°，将40°= 60°-20°代入两角差的正弦公式，整理得

评注：该题虽然消除了函数名的差异，但在通分整合过程中，又产生了角的差异，需要再消除角的差异.实践表明：解一道较难的三角问题，需要消除差异的往往不止一个.

例2（某四星级高中“三角变换测试”题）已知：求的值.

简析：测试反馈：有几个班级的学生得分率不足0.3，可见其难度.本题条件是两角和、两角差的正切，目标是二倍角的正弦之比，角与函数名都存在差异.一般学生对“角变换”都能想到，对函数“名变换”也知晓，但因解答程序不合理，仍然困难.有些同学从条件出发，可以求得tan2α，tan2β，但没有给出角的具体范围，需要分类的情形比较多，解答烦琐.以下给出两种正确的解法.

解法一：（切化弦）由tan（α+β）=-3，得sin（α+β）= -3cos（α+β），同理sin（α-β）=cos（α-β），代入目标式，得

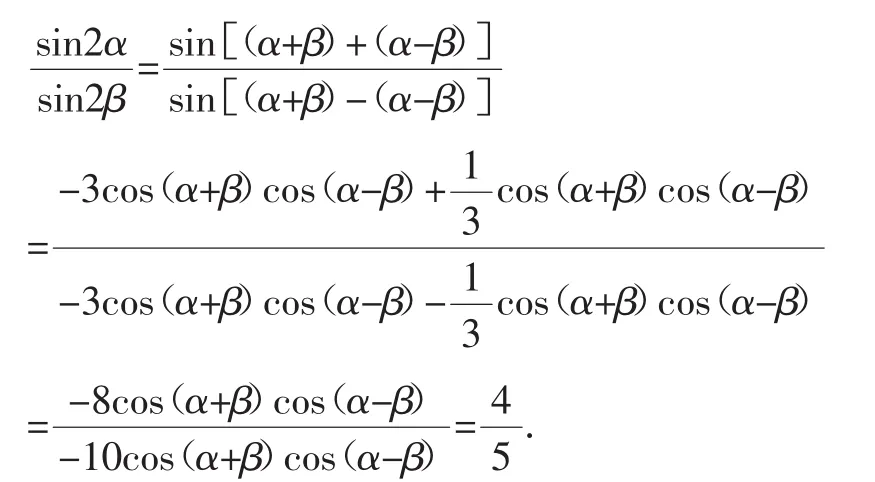
解法二：（弦化切）从目标出发，将目标角2α，2β转化为条件角α+β，α-β，再展开.

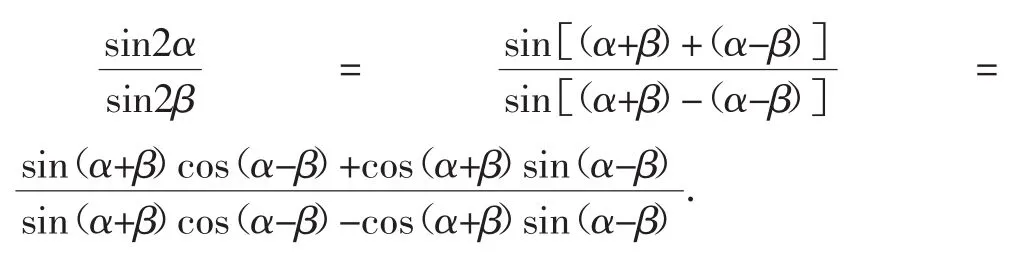
评注：本题切化弦、弦化切都可以，关键是解答程序要把握好.解法一是从条件出发，进行切化弦，求出了一个关系，代入目标式，归到“一个量”，再约分求解，是整体消除差异，而不是像有些学生那样，求出tan2α；解法二是从目标出发，通过角变换消除角的差异，展开后是一个奇次式，通过同除运算，把“弦”化成了“切”，消除函数名的差异，再把条件直接代入.

二、通过函数“名变换”和“消元法”，消除差异

众所周知，数学高考考查的侧重点之一是通性通法，“消元法”是处理“多变量”或“多字母”问题的通法，在三角函数的“多字母”问题中，出现的函数名、次数的差异，需要利用“消元法”并结合其他方法消除.

例3 （2016年江苏高考题14）在锐角三角形ABC中，若sinA=2sinBsinC，则tanAtanBtanC的最小值是_________.

简析：其一，条件“sinA=2sinBsinC”含三个角的正弦，目标“求tanAtanBtanC的最小值”含三个角正切的乘积，条件和目标之间的函数名有差异，可以通过“弦”化“切”消除.

其二，条件的左右两边的次数不齐，需消除差异，注意到有三个变量即三“元”，自然想到消元，消哪一个呢？如果消sinB（或sinC），展开后变为三次，难以整合，因此只能消sinA.再用两角和的正弦公式，得sin（B+C）= 2sinBsinC，展开sinBcosC+cosBsinC=2sinBsinC，形式为二次奇次式，等式两边可同除以cosBcosC，得tanB+tanC= 2tanBtanC ①.

同理，对于目标式的三“元”问题，自然要消元（tanA），得tanAtanBtanC=

将①代入②，设tanBtanC=x，tanAtanBtanC=y，得到函数关系式通过分离常数4，再利用基本不等式，可求得tanAtanBtanC的最小值是8.

评注：本题通过观察条件式与目标式，存在函数名、次数等的差异，通过函数名变换、消元，消除其差异，当然过程并非一帆风顺.其中，奇次式问题常用“同除”，求最值问题常结合基本不等式，在解题中发挥了重要作用.可见，解决这道高难度的填空压轴题，思路也很自然，这是缘于用了“消除差异”的策略，它在寻求问题的本质联系后进行自然转换.当然，解答本题也可以用“解析几何”、“基本不等式”等其他方法，这里从略.

三、通过三角函数的“角变换”和“升降幂变换”，消除差异

有些三角问题的次数有高有低，所给的角有二倍角、半角等，如何同时消除次数和角的差异呢？可以通过二倍角的变形式——升降幂公式，在次数升（降）的同时，角也相应变小（大），达成一种新的平衡.有时把一个角拆分为两个角，再用两角和与差的正、余弦公式，也能升“次”，达到消除差异.

简析：本题的角有二倍角（2θ）、半角两种，角的差异需要消除，一般是将其转化为单角（θ）.利用升降幂公式：

例5（1997年全国高考题18）的值为________.

简析：这是一道不查表求值问题，为分式形式，有三个非特殊角，三个角的联系为15°=7°+8°；正弦或余弦的次数有一次、二次.多元问题一般方法是消元，消哪个角呢？要消除次数的差异，只能消7°（见例3的分析），根据两角差的正、余弦公式，转变为二次式：sin7°=sin15°cos8°-cos15°sin8°，同理cos7°=cos15°cos8°+sin15°sin8°.把它代入原式，得tan15°=2-

评注：利用升幂、降幂公式，可以起到缩小、放大角的目的，因此，“升、降幂变换”往往与“角变换”联用，以消除差异.

四、通过三角形中边与角的相互转化，消除差异

对于三角形中的三角函数问题，有的已知边（或角），求角（或边），有的已知边、角混合问题，求边（或角）的最大（小）值等，需要消除其差异，究竟是“边”化“角”还是“角”化“边”，需要根据题目的特点，进行选择、优化.

简析：条件是含三个角A、B、C的正弦，目标是求角C的余弦；如何消除条件、目标中的差异，以沟通两者的联系呢？对于三个角的正弦函数，可以用正弦定理，把“角”整体转化为“边”目标中求角C的余弦的最小值，可以用余弦定理表示，也转化为边这样，就找到了条件、目标的联系——边.

评注：本题根据形式特点，利用正弦、余弦定理，把条件、目标式的三角函数中的“角”整体转换为“边”来处理，思路比较自然、明确.

例7（2010年江苏高考题13）在锐角三角形ABC中，A、B、C的对边分别为a、b、c则

简析：这道试题思维强度大，得分率低.

条件是边角混合问题，需要消除差异，边化角还是角化边，目标式为三个角的正切函数；若边化角，则为二次结构.

观察目标式：因可能要利用正弦、余弦定理，故要进行切化弦，并提取公因式，再通分，得

观察形式结构：分子、分母都是含有正弦的齐次式，可利用正弦定理，同时，对cosC用余弦定理，整理得

由①、②，通过消元（a2+b2或c2），得答案为4.

评注：当时许多考生解答受阻，其一，对于多字母问题不知如何处理，考生没能主动整理到形式其二，当时复习教学还很少涉及正弦定理与余弦定理的联用，学生意识不到.本题涉及三角形的边角关系，需要根据试题的形式、结构特点，合理选用两个定理.第一次对条件式通分后，选择余弦定理把角整体化为边，之后又对目标式切化弦，通分整合后，同时运用正弦、余弦定理，这一解题策略很重要.当然，本题若采用“特殊化”处理（令a=b），则可使解答更简洁、明快.

与人友好相处，要以诚相待、求同存异，治愈“三角疑难”病症（重、难点问题）的一剂良方是消除差异，它追求自然的解题，追求和谐之道.明道还需优术，其一，在“消除差异”指导下，要关注目标，理清脉络，通过选择三角变换（角变换、名变换和升降幂变换），通过消元，制定合理的解题程序；其二，消除差异的过程有一定的反复，需要有耐心；其三，三角问题往往免不了要结合通分、奇次式同除等常用的辅助手段，综合问题还需结合基本不等式、导数等常用工具.可见，一定的知识经验是解决问题的基础，需要我们不断累积，在解除疑难后奋力前行.

1.罗增儒.中学数学解题的理论与实践［M］.南宁：广西教育出版社，2008.