高中数学问题串教学模式的思考

☉江苏省溧水高级中学 李宽珍

高中数学问题串教学模式的思考

☉江苏省溧水高级中学 李宽珍

数学的发展过程实际上是一个不断发现问题、分析问题和解决问题的过程.数学的研究是从问题开始的，同样，数学的学习也是从问题开始的.数学教学过程实际上是引导学生发现问题、分析问题和解决问题的过程.因此，数学教学从本质来说是一个关于“问题”的教学.在教学过程中，我们可依据教学目标将教学内容设计成一系列问题，将这些问题排列成一个由浅入深、由易到难的问题串，以问题为导向，使学生通过对问题的思考和研究来实现教学目标，我们不妨把这一方法称之为“问题串”教学法.

一、“问题串”教学法

（一）“问题串”教学法的含义

“问题串”教学法是指根据教学目标，精心设计一系列的有效问题，把教学内容以问题形式呈现，以问题为导向，引导和推动学生进行思考和研究，从而使学生获得知识和能力的教学方式.问题串教学的中心任务是设计一个或一系列有效的问题，把教学过程组织成为“学生思考和研究问题”的过程.

“问题串”教学的基本特征是：学生的学习以问题为导向和起点；学生的学习过程是研究问题和解决问题；学生的交往是以问题为中心.在教学过程中，学生带着问题去思考和研究，新的知识在问题的解决过程中得到理解和掌握，学生的各种能力在问题的解决过程中得到提高，学生的数学素养和素质在问题的解决过程中得到升华.

（二）“问题串”教学法的意义

1.有利于激发学生学习的积极性

“问题串”教学法，顾名思义是以问题为主导的教学，通过问题的解决促进学生主动思考，积极探究，从而激发学生学习的积极性，诱发学生的探究热情，培养学生的学习兴趣.特别是提出的一些富有趣味性、挑战性的数学问题，可极大地激发学生学习的积极性.

2.有效地改变学生不良的学习方式

“问题串”教学法以问题为驱动，以学生活动为中心，在开放的学习环境中，学生自主的观察、实践、交流、研究，主动参与到“问题”的研究中，真正做到“独立思考、自主探索、合作交流、阅读自学”.变学生被动的接受式学习方式为主动学习方式.

3.符合学生的认知规律

建构主义认为，学习不是个体之间简单的传递和转移，而是学习者在自己已有的知识和经验基础上，通过新知识与原有知识经验的内化、吸收，来补充和丰富自己的知识结构.要学生实现知识的主动建构，把学科内容形成“问题”是较好的方法，并让学生去解决问题.在问题解决活动中，通过学生独立思考、主动探究，深入地激活自己的原有经验，使新、旧经验间双向的相互作用得以更充分、更有序地进行，这使得学习活动真正切入到学生的经验世界当中，问题的解决为新、旧经验的同化和顺应提供了理想的平台.

4.有效地培养学生的思维能力

思维能力是能力的核心.思维从问题开始，没有问题就没有数学思维，学生的思维活动是在解决问题的过程中展开的.美国数学家哈尔莫斯指出：“问题是数学的心脏”.苏格拉底则说：“问题是接生婆，它能帮助新思维的诞生.”问题能激化认知矛盾，启发学生思维.“问题串”教学法能有效地培养学生的思维能力.

5.有利于学生对知识的理解

从数学的发展过程来看，数学的发展是在不断发现问题和解决问题的过程中进行的，数学知识和思想方法都是在解决问题中提炼出来的.“问题串”教学法使学生在解决问题中，探寻数学知识的形成和发展过程，探求数学的本质，使学生对知识的理解更加深刻.

6.使教学过程简洁凝炼

“问题串”教学法，以问题为导向，使教学目标更加明确，任务更加具体，教学过程更加清晰，有利于学生抓住要旨，有利于教师驾驭课堂.

二、“问题串”教学法的基本教学模式

“问题串”教学法可以说是一种教学方法，也可以说是一种教学理念.教学形式可灵活多变，其教学模式可不拘一格，在教学中可根据教学的需要适当增加其他环节，如“回顾与反思”、“达标检测”等.“问题串”教学法常常有下列两种最基本的类型：

（一）“问题—研究”型

首先，由教师提出精心设计的问题串；然后，让学生自主研究与思考；最后，进行师生之间的合作与交流.如此反复进行.一节课可能要经历若干个“提出问题—自主研究—合作交流”的问题串教学环节.

案例1“等比数列的前n项和”的教学设计.（教材：苏教版普通高中课程标准实验教科书必修5）

教学过程：

活动一：创设情境，提出问题

课堂伊始，笔者讲了关于国际象棋起源的故事（故事情节略），并设计如下问题串：

问题串一：情境性问题串，引出问题.

问题1：棋盘上有多少麦粒数？

问题2：每格所放的麦粒数可以视为什么数列？

问题3：能否将上述问题抽象出一般情况？

师：如何计算这个算式？（学生思考）

问题4：我们要求的实际上是什么样的问题？我们是否可以找到一般的方法解决这一类问题？（点明课题）

设计意图：通过一系列的问题将故事情节与数列的相关知识点联系起来，从情境中看到数学问题.情境性“问题串”设计当然要体现情境性，一般来说要具备三个要素：①涉及未知领域，能启动学生思维；②具有真实性，让学生觉得亲切、自然；③基于学生已有的知识水平.这样的问题情境，能激发学生学习新知识的好奇心和求知欲，引发学生自主探究，让学生在解决问题中顿悟，提高学习新知的能力.

活动二：学生活动，体验数学

问题串二：方案性问题串，形成概念.

问题1：我们把问题一般化，即求Sn=a1+a2+a3+…+an，怎样求等比数列前n项的和？

（学生思考、讨论、交流）

问题2：我们在求解中，会遇到哪些障碍？

生（众）：未知量太多了.

问题3：对，量太多，这里有a1，a2，a3…，an，共n个不同的量，那么，怎样能让这里的量少一点？类似的问题，我们之前有接触过吗？

生3：等差数列求和.

问题4：好，等差数列中，也有n项，我们是怎么处理的？

生4：倒序相加法，用a1，n，d表示.

师：我们利用倒序相加，实现消项，最后转化为a1，n，d或者a1，an，d这三个基本量来表示.那么类比等差数列，等比数列是否也可以转化为三个基本量？

生5：用a1，n，q，转化为Sn=a1+a1q+a1q2+…+a1qn-2+ a1qn-1①.

师：我们还是遇到了问题，这里的项数太多，我们怎样来消项？

（继续引导）我们经常将已有的知识和方法当作探索新问题的基础，回顾一下等差数列、等比数列的通项公式、等差数列前n项和公式的推导过程，有什么共同的本质特征？

生（众）：消项，用首尾项或基本量表示.

（学生情绪高涨，思维目标明确：消项.）

问题5：很好！那我们应如何消项呢？利用的原理应该是什么？

师：好，我们能否围绕着定义，目标是基本量的最简形式，来实现等比数列求和的推导.请大家在白纸上探索进行推导，寻找不同的求和方法.

师：（3分钟后）同桌之间互相交流分享下，有没有不一样的收获？

生7：将Sn=a1+a1q+a1q2+…+a1qn-2+a1qn-1，整体乘以q，得qSn=a1q+a1q2+a1q3+…+a1qn-1+a1qn②.

问题6：你是怎么想到乘以q的呢？

生7：根据等比数列的定义，a2=a1q，a3=a2q，…，an=an-1q，每一项乘以q，往后挪了一项，①、②两式就出现很多相同的项，由①-②可得，（1-q）Sn=a1-a1qn，则Sn=

师：求解成功！下面用公式计算一下：S100=2+2+2+…+2（100个2相加）.

学生代入公式……发现分母为0！无意义！

问题7：是公式错了吗？（引导学生回顾公式推导过程，检验每一步的等价性）

生8：当1-q=0时，两边一定不能同除以1-q，此时只能代入最原始的公式，所以要进行讨论.

问题8：此方法有几个步骤？

问题9：我们成功地将等比数列前n项和转化为基本量a1，n，q的最简形式，但要注意分类讨论.大家还有其他的推导方法吗？

（学生探究、交流，教师巡视后，请一位学生板演）

问题10：此方法在转化为基本量过程中，需要注意什么问题？

设计意图：这一组问题串旨在引导学生站在一个高度展开对等比数列前n项和的探究，必须要求问题能贴近学生的“最近发展区”，使得学生的思维自然流淌.当学生推导出求和公式时，设计问题串，让学生自己去发现公式使用的局限条件.问题1、2、3展示学生解决这个问题的困惑；问题4引导学生类比等差数列，提炼出求和的本质思想即为化简；问题5则明确推导依据，并引发学生探讨，进而进行合作交流；问题6、7让学生展示其思维过程，通过自己的建构、纠错来完善公式，进而更好地发掌握公式的本质，同时还要引导学生反思出现此问题的原因；问题9、10则培养学生的归纳、概括的能力，在获取知识的同时也提高能力.

活动三：完善公式，建立数学

问题串三：方法性问题串，辨析概念.

问题1：完成下列判断，看是否正确？

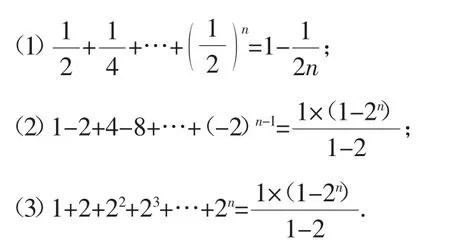
问题2：从中你能得到哪些启示？在运用公式求和时要注意哪些问题？

问题3：什么时候用公式①？什么时候用公式②？

设计意图：设置方法性问题串，让学生在学完新知识后达到进一步巩固练习的作用.

活动四：数学变式，运用数学

问题串四：变式性问题串，巩固概念.

问题1：你能否运用公式解决国王赏麦故事中的问题？

例题在等比数列｛an｝中，完成下列表格：

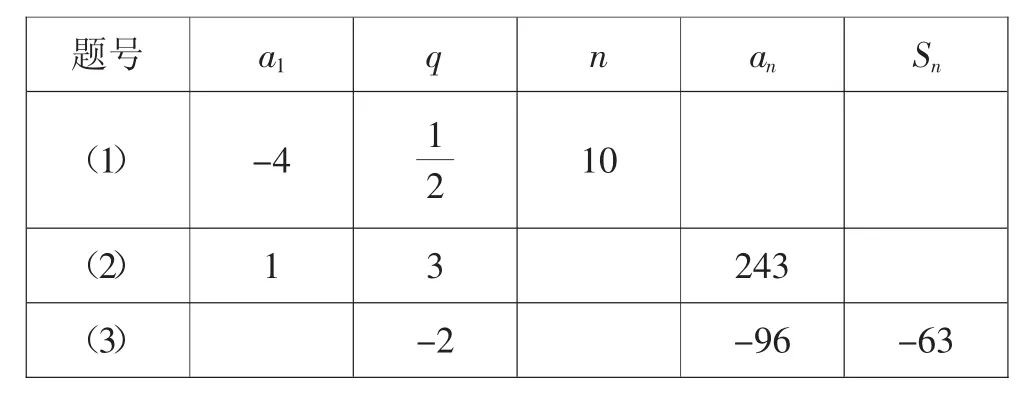
题号 a1 q n an Sn（1） -4 1 2 10（2） 1 3 243（3） -2 -96 -63

问题2：与等差数列求和公式类似，有两种形式，涉及几个量？能帮我们解决什么问题？

设计意图：进一步通过问题串的形式加强对所学知识的理解和建构.

活动五：回顾反思，理解数学

问题串五：反思性问题串，升华概念.

问题：通过这节课你学到了哪些新知识？掌握了哪些新方法？用新知识解决问题时要注意哪些？还有哪些困惑的地方？

（二）“问题—自学”型

首先，教师提出精心设计的问题；然后，让学生自学与思考解决问题；最后进行师生之间的合作与交流.

案例2“数列的概念与简单表示”的教学设计.（教材：苏教版普通高中课程标准实验教科书《数学》必修5第二章2.1）

教学过程：（1）提出问题.

学生自学课本P28～31，思考下列问题：

①什么叫数列？什么是数列的项？什么叫数列的首项？数列与数集有何区别？

②数列的一般形式是什么？

③什么叫数列的通项公式？an与｛an｝表示的意义是什么？

④数列按项数的多少来分可以分为几种数列？按项的大小来分可分为几种数列？

⑤如果把数列的通项公式看成一个函数解析式，那么其图像有何特征？

⑥什么叫数列的递推公式？你能进行简单的描述吗？

⑦完成课本P31的练习.

（2）学生自学.

学生带着问题自学课本，并完成相应的练习.

（3）合作交流.

在学生自学的基础上，由学生提出疑难问题，由其他学生进行解答，或由教师释疑解惑.同时教师根据教学的重点和难点再提出相关问题让学生思考，以此来检查学生的自学效果，同时深化学生对知识的理解，教师通过反馈的信息予以必要的讲解和回授.

（4）回顾反思.

为了使学生进一步理解所学的知识并形成知识系统，教学中可引导学生进行必要的归纳与反思.如本节课可进行如下归纳：

“问题串”教学法让学生带着问题进行学习，通过自主研究和合作交流，促进学生对知识的理解和保持，使学生的能力得到提高、智力得到发展、素质得到升华；同时学生还会收获探究的乐趣、交流的快乐、成功的喜悦.

三、“问题串”教学法的几点说明

（一）“问题串”教学法的基本过程

“问题串”教学是以问题驱动，使学生进行独立思考和自主研究获取知识和能力.根据建构主义学习理论，学生的学习过程应将自主研究与合作交流结合起来，通过自主研究使学生进行主动的知识建构，通过合作交流促进学生对知识的深刻理解、促进学生认知能力的发展.因此，“问题串”教学的基本过程是“提出问题—自主研究—合作交流”三个基本环节.一般来说，一节课可以由一个“问题串”教学单元或多个“问题串”教学环节构成.

（二）“问题串”的设计的基本原则

1.准确性原则

教师所提出的问题应依据课程标准，将教材中的知识以问题形式呈现.提出的问题必须符合教学目标中的要求，注意突出教材中的重点，使学生在解决问题的过程中实现教学目标.设计的问题要求通俗易懂，表达准确，言简意赅.避免出现词不达意，模棱两可的表述.

2.“最近发展区”原则

“问题串”的设计必须从学生现有的知识水平和经验出发，难度要适中，所提出的问题是学生经过努力可以解决的.运用前苏联著名的教育家和心理学家维果茨基的最近发展区理论，教师要了解学生的现实水平和潜在的发展水平，为学生创设最近发展区，为学生提供脚手架.对过难问题要设计合适的过渡问题，问题的设置注意由浅入深，分层推进，螺旋上升.

3.启发性原则

所提出的问题应能激发学生思考，使学生通过对问题的研究，揭示问题的本质、领悟问题中所蕴含的数学思想方法.使学生在问题的研究中产生新的生成性问题.

1.中华人民共和国教育部.普通高中数学课程标准（实验）［M］.北京：人民教育出版社，2003.

2.李志敏.课堂教学有效提问的方法与艺术［J］.中学数学研究（广州），2011（12）.

3.李宽珍.主线·层次·延伸——由“等比数列的前n项和”的教学设计谈问题串的设置［J］.中小学数学，2015（5）.