稳步推进求发展 积极探索谋新篇
——2016年高考数学试卷总体评析与教学启示
2017-01-12安徽省灵璧第一中学安徽省宿州市教科所
☉安徽省灵璧第一中学 郑 良☉安徽省宿州市教科所 王 锋
稳步推进求发展 积极探索谋新篇
——2016年高考数学试卷总体评析与教学启示
☉安徽省灵璧第一中学 郑 良☉安徽省宿州市教科所 王 锋
一、总体评价
2016年全国各地高考数学试卷共有10套19份(文、理科各算1份,江苏文理科合卷,理科有卷II(附加题)),分别是教育部考试中心统一命制的试题3套:全国卷I(河南、河北、山西、江西、安徽、湖南、湖北、福建、广东等省区),全国卷II(陕西、重庆、辽宁、吉林、黑龙江、宁夏、甘肃、青海、新疆、西藏、内蒙古、海南等省区),全国卷III(云南、贵州、广西等省区),自主命题7套(北京、天津、上海、浙江、江苏、山东、四川等省区).总体来说,各套试卷保持一贯风格(新增全国卷III),稳步推进,适度发展创新,使学生心态平稳,较快地进入考试状态,发挥真实水平;立足基础,尽可能使每个学生都得到基本分,彰显人文关怀;着眼能力,通过思维层次的甄别,凸现学生能力,突出高考的测试与选拨功能;在延续主干知识重点考查的同时兼顾知识面的覆盖,不偏不难,有效避免“猜题押题”“题海战术”;频现经典、兼顾冷点,体现了命题专家坚持改革与创新的尝试;关注应用,体现了数学“来源于生活,应用于生活”,让学生在学以致用中理解升华;文化创新,彰显数学学科育人价值,促进素质全面发展;突出本质、强化综合,从整体角度、系统高度考查学生的综合素养,有利于发挥高考的导向作用.
二、试题特点与应用举例
《义务教育数学课程标准》(2011年版)提出“四基”(基础知识、基本技能、基本思想、基本活动经验),“四能”(发现问题的能力、提出问题的能力、分析问题的能力、解决问题的能力),高中学生理应具备更高的能力与素养.R.柯朗和H.罗宾指出:“数学,作为人类思维的表达形式,反映了人们积极进取的意志、缜密周详的推理以及对完美境界的追求.它的基本要素是逻辑和直观、分析和构作、一般性和个别性.”[1]知己知彼,百战不殆.限于篇幅,本文不再对全国各地数学卷考点分布情况进行统计,仅就试题显著特点进行概述与部分试题例析与链接.
1.立足基础
基础扎实,能力才能提升.各地数学卷整体上难度略有降低,压轴题运算量减少,十分注重对“四基”与“四能”的考查.如集合运算(19份)、复数运算(17份,浙江卷文、理科无)和向量运算(19份)等基础知识与方法,程序框图(15份,浙江卷与上海卷文、理科无)、三视图(17份,上海卷文、理科无)、线性规划等仍然是知识考查的热点.此类试题大多为客观题的靠前部分,需要解题者通过审题发现问题的一般与特殊,实现“小题小(巧)做”,谨防“青蛙效应”引起时间悄然流逝.
例1(北京卷文科第2题)复数=( ).
A.i B.1+i C.-i D.1-i
点评:本题常规解法是分子、分母同乘以分母的共轭复数实现分母实数化,充分观察分子、分母中复数的实部与虚部的联系,用“i2=-1”局部逆代换,通过约分实现分母实数化复数的本质是“i2=-1”,很多学生只知道复数的代数形式和四则运算,使复数的学习与运用成为机械化的操作,索然无味.若从复数的三角形式来理解“i2=-1”,复数的本质是对平面局部做旋转和缩放,另解清楚自然,水到渠成.将其变式,利用几何意义可解四川卷文、理科第15题(“伴随点”姊妹题).
例2(天津卷文、理科第7题)已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则的值为( ).
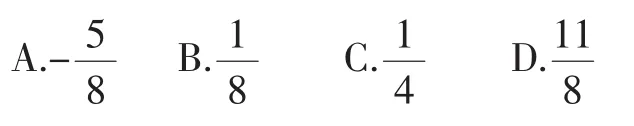
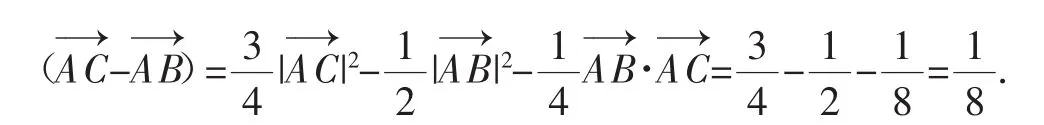
解法2:以B,C的中点为坐标原点,以B,C所在直线为x轴,建立平面直角坐标系,如图1所示,则所以(1,0),故
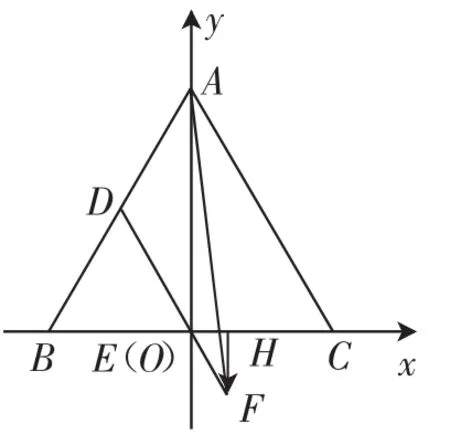
图1
点评:本题考查三角形的性质,平面向量基本定理、线性运算与数量积,考查考生的运算能力.解法1以为平面向量的一组基底(基向量的选择要尽可能容易表示出目标向量),将目标式中向量“标准化”,彰显化归思想的力量,对可直接展开,利用解法2为解析法,将几何问题代数化,通过运算来研究几何性质,数形结合以不变应万变;解法3利用“互相垂直的两个向量的数量积为零”简化运算,利用共线定理往已知结论上转化,体现了特性在解题中的作用;解法4利用数量积的几何意义(a与b的数量积等于|a|乘以b在a方向上的投影),直观快捷.以上解法是处理(平面、空间)向量问题的基本方法.解题要有模式,但不能囿于模式,要具体问题具体分析,如山东卷文科第13题用解析法较好(若用几何意义沦为解三角形问题),山东卷理科第8题代数法与几何法运算量相当.
2.突出本质
《普通高中数学课程标准(实验)》提出:“形式化是数学的基本特征之一,在数学教学中,学习形式化的表达是一项基本要求,但不能只限于形式化的表达,要强调对数学本质的认识,否则会将生动活泼的数学思维活动淹没在形式化的海洋里……”.“高中数学课程应该返璞归真,努力揭示数学定义、法则、结论的发生、发展过程和本质.”各地数学卷都突出考查数学(尤其是核心)定义和核心思想方法的掌握与运用,以及对数学本质的理解与感悟,这就要求学生能透过现象看本质,数学地理解、数学地思考、数学地表达.
例3(浙江卷理科第5题)设函数f(x)=sin2x+bsinx+ c,则f(x)的最小正周期( ).
A.与b有关,且与c有关 B.与b有关,且与c无关
C.与b无关,且与c有关 D.与b无关,且与c无关
点评:本题考查三角函数的周期性.深刻理解正弦(型)函数、余弦(型)函数、正切(型)函数的图像与性质,函数的图像变换是解决问题的关键.不少教师认为本题重在考查周期函数和与差函数的周期公式,即在f(x)= g(x)+h(x)中,(其中[Tg(x),Th(x)]、(Tg(x),Th(x))分别表示函数g(x)的最小正周期与函数h(x)的最小正周期的最小公倍数、最大公约数).笔者认为命题者意在考查函数y=|sinx-m|+c的图像与性质,因为y=sinx既是轴对称图轴,又是中心对称图形,将其在平衡线一侧的图像沿着平衡位置翻折,其周期减半.考虑到y=sinx的平衡位置为直线y=0,故需对参数b是否为0分类讨论.
例4(上海卷理科第18题)设f(x),g(x),h(x)是定义域为R的三个函数,对于命题:①若f(x)+g(x),f(x)+ h(x),g(x)+h(x)均为增函数,则f(x),g(x),h(x)中至少有一个为增函数;②若f(x)+g(x),f(x)+h(x),g(x)+h(x)均是以T为周期的函数,则f(x),g(x),h(x)均是以T为周期的函数,下列判断正确的是( ).
A.①和②均为真命题
B.①和②均为假命题
C.①为真命题,②为假命题
D.①为假命题,②为真命题
点评:两个函数单调性相同时,其和函数的单调性与每个函数单调性相同,其差函数不一定具有单调性,这与每个函数增(减)的幅度有关.构造反例,应从每个函数的增(减)幅度入手.记F(x)=f(x)+g(x),G(x)=f(x)+ h(x),H(x)=g(x)+h(x),则f(x)=考虑最简单的函数载体——线性函数,其单调性取决于直线斜率的符号.将定义域R分成三段(抽屉原理),函数f(x)、g(x)、h(x)分别在第一段、第二段、第三段上是水平的射线、线段、射线,而在其余的部分,三个函数均为斜率为1的线段或射线,那么在每一段上,F(x),G(x),H(x)均为斜率为1或2的线段或射线.若考虑函数严格单调递增,只需将水平的、斜率为1的线段或射线的斜率改为斜率为-1、2即可.如f(x)=②由f(x+T)即函数f(x)是周期为T的周期函数,同理可得g(x),h(x)为周期函数(周期函数的和与差函数必定是周期函数).如该卷第13题:设a,b∈R,c∈[0,2π),若对任意实数x都有则满足条件的有序实数对(a,b,c)的组数为_________.若从恒成立角度求解,则会陷入繁杂的计算.在y= Asin(ωx+φ)+b(A>0,ω>0)中,A、ω、φ、b分别决定函数的高度、宽度(周期)、初始位置、平衡位置.将几何表征转换为代数表征,即函数的图像与函数y= asin(bx+c)的图像重合,其必要条件是高度和宽度必须一致,起点相差周期的整数倍,结合诱导公式及[0,2π)的区间长度为一个周期,说明c取值唯一.因此本题表象是枚举法,本质为对应,利用计数原理得有序实数对(a,b,c)的组数为2×2×1=4,体现出思维的深刻性.
3.注重推理
推理是直觉思维与逻辑思维的综合体现,包括合情推理(归纳推理、类比推理)和演绎推理等.数学是思维的科学,数学教学是数学思维的教学.数学地思考就是逻辑推理(从给定的前提条件出发,在推理过程中遵守逻辑规律、规则,正确地得出结论的推理)的表现.
例5(上海卷理科第11题、文科第14题)无穷数列an由k个不同的数组成,Sn为an的前n项和,若对任意n∈N*,Sn∈{2,3},则k的最大值为__________.
解:由题意知,k最大当且仅当Sn={2,3}(否则,当Sn={2}时,则有时同理).当Sn={2,3},有两种情况:当S1=a1=2,则必有ai=1(i≥2),还存在aj=-1,且数列{an}中仅有首项为2,1与-1彼此相间且先出现1,数字0可任意插入;当S1=a1=3,则必有ai=-1(i≥2),还存在aj=1,且数列{an}中仅有首项为3,-1与1彼此相间且先出现-1,数字0可任意添加.无论哪种情况,k的最大值为4.
点评:学生可能会通过列举法归纳出k的最大值为4,结论是否正确?为什么?通过正反思维、理性分析、逻辑推理锁定数列{an}的构成规律,证实发现.推理是数学的生命线,无处不在.直接考查数学推理的试题有全国卷II理科第15题(文科第16题)、北京卷理科第8题(利用对应对称性)、北京卷文科第8题(正反思维)等,当然也可以把结论当作条件,实现整体结构、思想方法上的融会贯通,如北京卷文科第18题第(III)问等.
4.强化思想方法
高考试题由“知识立意”到“能力立意”,并逐步发展能力的内涵,不断加大考查的力度.很多试题殊途同归,只有通晓相关定义,理解数学思想方法,才能随心所欲,找到优美的、本质的解法.高考中的数学思想主要包括:数形结合思想、分类与整合思想、化归与转化、函数与方程、特殊与一般思想、有限与无限思想、或然与必然思想等,数学基本方法有:待定系数法、配方法、换元法、割补法、反证法等.
例6(天津卷文科第5题)设x>0,y∈R,则“x>y”是“x>|y|”的( ).
A.充要条件
B.充分而不必要条件
C.必要而不充分条件
D.既不充分也不必要条件
解:x>|y|等价于-x
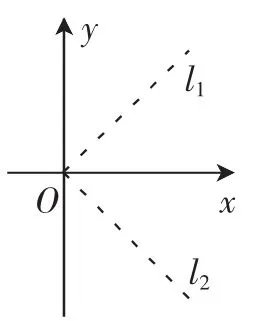
图2
由于x>0,当x>y时,取x=1,y=-2,不满足x>|y|;
反之,当x>|y|时,有x>|y|≥y,即x>y成立.故“x>y”是“x>|y|”的必要而不充分条件.
点评:判断充要条件的方法有三种:①定义法(命题p与命题q相互推出情况),②命题法(构造新命题:若p则q,通过判断原命题与逆命题的真假确定),③集合法(以p、q所包含的对象构成集合P、Q,通过判断集合P、Q的包含关系确定).三种方法表现形式不同,但逻辑本质(蕴含关系)相同,可对具体问题具体分析.一般说来,实数问题往往采用数形结合思想(形的直观和数的精确双管齐下)与集合法.反例怎么找?先将命题p、q等价转化,从隐形走向显性.通过判断两者差异,寻找符合条件而不符合结论的部分.类似的有天津卷理科第5题,江苏卷第9题(代数角度解三角方程,几何角度确定交点个数)等.
5.重视变形能力
数学是运算的科学,而运算的核心是恒等变形,相等与不等是对立统一的.因何而变,变向何方?变形就是对问题数学地理解、数学地思考基础上数学地表达.
例7(浙江卷文科第20题)设函数f(x)=x3+1 1+x, x∈[0,1].证明:
(1)f(x)≥1-x+x2;
(2)证法1:由0≤x≤1得x3≤x,故f(x)
由(1)得f(x)≥1-x+x2=又因为所以f(x)>
(2)证法2:f(x)=x3+则f′(x)=3x2-是(0,1)上增函数,由f′(0)=-1<0,f′(1)=知存在唯一实数x0∈(0,1)使f′(x0)=0,故函数(fx)在[0, x0]单调递减,在[x0,1]单调递增,又(f0)=1,(f1)=所以f(x)在[0,1]的最大值为
当x∈[0,1]时,由f′(x0)=0,即解得所以f(x)的最小值f(x0)
点评:(1)利用代数式恒等变形和不等式放缩完成证明.(2)适当利用代数式放缩来证明,要注意放缩的方向与精度,尤其要注意取等条件,如x3≤x在x=1时等号成立,f(x)≥1-x+x2当且仅当x=0时等号成立当且仅当时等号成立.放缩方向本质为同向不等式可加性(符号法则),一般不可调整,而放缩的精度要结合要求设定,如f(x)的本质是f(x)max≤取等条件为x=1,证法1中利用增量法,而f(x)>的本质为f(x)min>,f(x)的最小值点能够确定,但最小值不易化简,证法2利用等量代换,将目标(函数)式用我们熟悉的(函数)式替代或拟合.
6.频现经典
很多问题具有典范性、示范性,能体现学科(知识、思想方法)的精髓,百考不厌,常考常新.如函数的“极值点偏移”问题,可逆用函数的单调性(构造函数、等量代换、化归与转化)解决,可也用对数平均不等式处理,其实施步骤、逻辑原理等仍有待挖掘与提升.如全国卷I理科第21题第(2)问即为“极值点偏移”问题,同样取整函数也出现在全国卷II文、理科第17题.经典需要传承发展,文化需要继承弘扬,如全国卷II文科第9题(理科第8题)“秦九韶算法”程序框图问题,全国卷III理科第12题的背景是“卡特兰”计数(体现了一一对应与构造),江苏卷第22题(圆锥曲线中对称点)、浙江卷理科第18题(最小值函数).
7.强化综合
因为高考具有选拔功能,难题设置势在必然.在知识的“交汇点”设置问题成为高考命题的趋势,不仅增加了知识的覆盖面,更检测了学生对数学知识、思想方法的整体内化水平.一般客观题往往由两到三个知识点交汇而成,解答题由更多内容无缝对接、巧妙融合.如四川卷理科第19题,将数列、圆锥曲线以及不等式进行综合,能较好地考查学生的知识体系是否完备,同时也考验学生的心灵素质.
8.严谨表达
数学具有高度的抽象性、准确性(逻辑的严密性,结论的确定性)、应用的广泛性,数学是一门语言(包括自然语言、符号语言、图形语言等).数学地表达是数学交流沟通的重要方式,命题者试图通过表达来检测学生思维的广度、深度、严谨程度,但遗憾的是,很多学生只能意会,不善甚至不能言传,主要原因有:教师没有足够的重视与示范而导致“哑巴”数学;学生学习的不求甚解导致“不拘小节”积习难改;各学科(如语文、物理等)不能齐头并进等.如立体几何中,证明线面垂直的条件为直线垂直于平面内的两条相交直线,缺少“相交”,前提条件错误导致推证无效.高考试题具有推证规范性、精确化的趋势,如确定方程根的存在一般要求给出根的有穷区间(区间的端点为具体的实数).
例8(江苏卷第19题)已知函数f(x)=ax+bx(a>0,b> 0,a≠1,b≠1).
①求方程f(x)=2的根;
②若对于任意x∈R,不等式f(2x)≥mf(x)-6恒成立,求实数m的最大值;
(2)若0<a<1,b>1,函数g(x)=f(x)-2有且只有1个零点,求ab的值.
解:(1)①方程f(x)=2的根为x=0(过程略);②实数m的最大值为4.
(2)方法1:因为函数g(x)=f(x)-2只有1个零点,而g(0)=f(0)-2=a0+b0-2=0,所以0是函数g(x)的唯一零点.因为g′(x)=axlna+bxlnb,又由0
令h(x)=g′(x),则h′(x)=(axlna+bxlnb)′=ax(lna)2+bx(lnb)2,从而对任意x∈R,h′(x)>0,所以h(x)=g′(x)是(-∞,+∞)上的单调递增函数.
于是当x∈(-∞,x0)时,g′(x)
若x0<0,则于是又g(loga2)= aloga2+bloga2-2>aloga2-2=0,且函数g(x)在以和loga2为端点的闭区间上的图象不间断,所以在和loga2之间存在g(x)的零点,记为x1.因为0 若x0>0,同理可得,在和logb2之间存在g(x)的非0的零点,矛盾. 因此,x0=0.于是故lna+lnb=0,所以ab=1. 方法2:因为g′(x)=axlna+bxlnb,又由0 当x→-∞时,ax→+∞,所以g(x)→+∞;当x→+∞时,bx→+∞,所以g(x)→+∞; 又g(x)在R上的图像不间断,且g(0)=f(0)-2=a0+b0-2=0,所以x0=0,故ab=1. 方法3:因为函数g(x)=f(x)-2只有1个零点,即ax=2-bx有且只有一个解,而函数m(x)=ax,n(x)=2-bx分别是过定点(0,1)的下凸函数,上凸函数,故两个函数在x=0处的切线重合.而m(x)、n(x)在点(0,1)处的切线方程分别为y=(lna)x+1、y=(-lnb)x+1,所以有lna=-lnb,即lna+lnb= 0,所以ab=1. 点评:对于第(2)问,方法1通过反向思维,利用排除法锁定x0,理由充分,过程详实;方法2根据函数的单调性,利用图像上升与下降(学生初中时对单调性的几何映像),理由不如解法1充分;方法3分离函数,根据函数凸凹性确定其公切线重合,结论是正确的,但规范的证明要用到高等数学知识.因此,从图看出来的结论不能替代证明,要用代数语言来精确表征. 9.关注应用 应用题的设计需要符合“贴近生活、背景公平、控制难度”.因为学生生活环境不同,对生活经验的感知与理解程度差异较大,往往难以确定贴近所有学生生活的载体,无法保证背景公平;同时学生的阅读能力、抽象水平整体偏低,往往导致难度的失控,试卷的区分度、信度、效度不高,这也导致与应用相关的高考题(主要是应用题)在非议中裹足不前,甚至有萎缩的可能.目前,高考卷中很多应用问题都经过命题者反复的抽象与改编,就是成熟的数学模型,缺乏原生态的数学味.欣喜的是,江苏卷与上海卷保持一贯关注应用的风格,并开展积极探索,其他各省市将应用问题主要集中在概率与统计部分. 10.适度创新 《考试大纲》指出:“既考查中学数学的知识和方法,又考查考生进入高校继续学习的潜能.”命题专家往往通过“自定义”信息题考查学生即时学习的能力.这类问题需要对信息提取,理解,对所给的信息进行抽象、加工,然后对所要解决的问题确定化归方向,逐步转换,进而有效输出.如全国卷III理科第12题(规范01数列),北京卷理科第20题(G时刻),四川卷文、理科第15题(伴随点),上海卷文科第22题(无穷互补数列)等,全国卷III文、理科第4题(识图、用图能力)等. 11.几点商榷 高考试题对中学数学教学具有导向功能.高考数学试题以下问题值得商榷:(1)运算量大,书写内容多.总体来说,每份试卷都需大量的运算和繁多的书写,耗费学生大量的时间与精力,此种现象助推教学的异化——题海战术,把思维能力的考查演变为机械操作熟练度的比赛.工具化的学科教育也许是有效教学,但绝不是好教学,因为他缺乏善良的意志.因此,建议减少试题数量,提高思维含量.(2)客观题多,主观开放题少.学科教育是教育的一部分,具有智慧生命.目前,高考试题为了避免人为因素引起的不公平,片面追求客观化、数量化,导致一些学生客观题功亏一篑,被冰冷的分数掩盖、埋没.建议去掉选择题,减少填空题数量,通过以主观题为载体的思维对话(自主招生试题与面试作了有益的尝试),切实挖掘学生真实的情感与能力.(3)评分标准要透明、统一.评分标准关乎考生的命运,备受师生关注.以前高考答案(册)中有赋分标准,使学生学习知根知底,教师教学心中有数.通过解读评分标准,使师生在现实中实现理想.省(市)考试院可对赋分的依据、上一年(近几年)学生高考的情况进行通报,使师生抬头看路,有的放矢.各省评分标准尽可能统一,以免造成师生无所适从.(4)试水速度缓慢.锐意改革,逐步推进,稳中求变是当前高考卷试水题的发展规律,以数学文化为例,主要以数学史和经典数学问题为载体,对数学史是浓墨重彩还是蜻蜓点水?若用文言文考查,异化到语文古文领域;若直接翻译为现代文,其功能无从谈起.如何把握好度,开拓更多途径值得深思. 上面罗列了高考数学试题的部分特点,可作为(新授课与复习课等)教学的重要参考.如夯实基础,构建知识网络体系;感悟数学思想,理解数学方法;适度形式化,注重挖掘本质;培养创新意识,突破知识交汇等,其作用与实施办法不再赘述,此处强调四点. 1.强化阅读理解能力培养 高考在考查基础知识的同时,着重考查诸多方面的能力,而要让这些能力在解题过程中得以充分发挥,离不开对题目的阅读理解.数学阅读障碍导致不少学生出现数学学习困难,读不懂,读不通,不能正确完整理解题意,正是考生认为试题偏难原因之一.教师要深入分析学生数学阅读障碍的原因,给予系统性的指导策略.因此,教学中要加强阅读理解能力训练,教会学生阅读(泛读,细读、精度)的方法,使学生获得源头活水. 2.教师自觉深入学习反思 当前教师多是埋头教学无暇三思,对新问题不求甚解,企图通过题海战术让学生感知、感悟、理解、升华,把压榨学生当作认真负责.教育作为一门人文科学,要立足于人性,从而自然的教育便是“爱”,爱让教师要敢于担当,乐于奉献.教师要不断地学习,解决、反思、整合问题,时时刻刻、事事处处站在系统的高度讲授知识,让知识总是以“系统中的知识”的面目出现在学生面前.教师要着眼于知识之间的联系和规律,使学生从系统的高度领悟和把握知识进行思考,做到八方联系,浑然一体,达到浮想联翩、思潮如涌的思维状态.在此过程中,教师要抓住机会向学生学习,丰富自己的理解,实现教学相长. 3.重视概念理解推进教学 《普通高中数学课程标准(实验)》明确指出:“高中数学课程应该返璞归真,努力揭示数学概念、法则、结论的发展过程和本质.”概念是思维的基本形式,具有确定研究对象和任务的作用.数学概念则是客观事物中数与形的本质属性的反应,是构建数学理论大厦的基石,是导出数学定理和数学法则的逻辑基础,是提高解决问题能力的前提,是数学学科的灵魂和精髓.概念是解题的出发点与归宿,无论怎么强调都不为过.但要注意每一个数学概念都有一定的发展过程,不同学段的学生对同一概念的理解也应当是不同的,这是学生的认知水平和认知规律所决定的. 4.加强自主探究能力训练 教育家苏霍姆林斯基说过:“没有自我教育,就不是真正的教育.”教师不要急于用自己的思想去同化学生的片面观点、错误认识,而应站在学生的立场去顺应学生的思维,掌握其思维轨迹,给学生一定的探究平台、时间和空间,让学生在探究中发现错误,寻找错因,探究正解,在辨析中明理,在理解中内化,在纠错中升华. 1.[美]R.柯朗,H.罗宾.什么是数学——对思想和方法的基本研究[M].左平,张饴慈,译.上海:复旦大学出版社,2005. 2.朱恒元.星垂平野阔 月涌大江流——2012年全国各地高考数学试题的特点和启示 [J].中国数学教育(高中版),2012(7/8). 3.郑良.强化变形意识 明晰变形方向 深化变形理解 提升解题能力[J].数学通讯(教师版),2015(3). 4.孙勇军,许晓天.注重基础创新 达到平稳过渡——2015年安徽省高考数学试卷评析[J].中学数学(上),2015(8).三、教学启示
