加权核范数的矩阵恢复正则化算法

张娅楠，赵建伟，曹飞龙

(中国计量大学 理学院，浙江 杭州 310018)

加权核范数的矩阵恢复正则化算法

张娅楠，赵建伟，曹飞龙

(中国计量大学 理学院，浙江 杭州 310018)

在压缩感知、矩阵恢复等研究领域，弹性正则化方法引起了广泛的关注.由于该方法可以避免数据建模时(特别是解决复杂问题时)解出现大的波动，从而被视为解决相关问题的优秀方法之一.针对以上情况，提出基于Schattenp-norm最小化的矩阵恢复的弹性正则化模型，旨在加强解决复杂问题时的解的稳定性并改进矩阵恢复研究领域中基于核范数最小化逼近秩函数这一传统方法的缺陷.同时，为了解决提出的非凸模型，采用交替迭代算法和MM算法求解所提出的模型.实验结果表明，所提出的算法能够有效地恢复测量值较少的矩阵.

矩阵恢复；弹性正则化；Schattenp-范数；交替迭代算法；MM算法

近几年，随着压缩感知和稀疏表示研究的兴起，低秩矩阵恢复问题已成为机器学习[1-3]、模式识别[4-5]以及计算机视觉[6-10]等领域的研究热点之一.

而作为矩阵恢复问题的特殊问题，矩阵填充问题同样在很多实际问题中有着广泛的应用，著名的Netflix问题[11-13]便是其中最经典的案例.该问题极大地刺激人们关于矩阵恢复问题研究的热情.

低秩矩阵最小化问题旨在从有限的信息中恢复出一个未知的低秩或近似低秩的矩阵.当矩阵的测量值已知时，低秩矩阵恢复解决如下问题：

min rank(X)

s.t.A(X)=b.

(1)

其中A：Rm×n→Rs(s≪mn)是一个线性算子，向量b∈Rs.

不幸的是上述问题是NP难问题.因此，求解这个问题是比较困难的.参考压缩感知中的类似经验[14-15]，人们通过用核范数逼近秩函数，转而求解下面的启发式优化问题(NNM)：

min‖X‖*

s.t.A(X)=b.

(2)

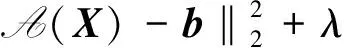
(3)

其中λ为大于0的正则化参数.

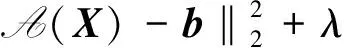
(4)

该方法通过用非凸项来替代核范数逼近秩函数取得比NNM更加准确的恢复效果.而基于TNNR的算法也应用在了视频背景建模[26]和图像分类[27]等领域.然而，对于一个具体的奇异值，TNNR对于是否将其作为正则化的一项只是做了一个二元决策，TNNR显然也不够松弛.因此，TNNR虽然通过截掉较大的奇异值对NNM进行了改进，但是这种粗鲁的方法并没有考虑到剩下的奇异值对恢复结果的贡献，所以这种方法在效果上也不尽如人意.

近几年，一种基于Schatten p-norm最小化的非凸正则化方法[28-30]被用来替代传统的NNM，Schatten p-norm 最小化可以表示如下:

(5)

在压缩感知领域，受回归问题的影响，Zou等人[31]提出了弹性正则化的方法，其主要思想是将传统的l1-l2模型与岭回归的惩罚项相结合以达到控制解的稳定性的效果，具体模型可以表示为

(6)

(7)

结合以上模型和算法的优势，本文将主要研究基于Schatten p-norm最小化的矩阵弹性网正则化算法.鉴于一个适当的p可以使得Schatten p-norm最小化在测量值较少的情况下得到与基于NNM的算法相比更加准确的效果，而矩阵弹性网正则化模型可以在待恢复矩阵相关性较高的情况下控制解的稳定性，因此本文研究的基于Schatten p-norm的弹性网模型期望可以在控制解的稳定性的同时得到与MEN相比更加准确的恢复效果.

在本文中，我们首先提出一个基于Schatten p-norm最小化的矩阵弹性网正则化模型(简便起见下面表示为MEN-Sp)，当矩阵秩较低时，这个模型可以得到更加稳定的解，此外，当测量值较少时，它也可以得到相比MEN更加准确的效果.之后，我们构造了两种算法来求解这个非凸模型，一种是交替迭代算法，一种是基于MM算法框架的加权软阈值算子法.我们还将通过实验来说明MEN-Sp在恢复测量值较少的矩阵时与凸优化模型相比的优势，而在较复杂情况下解的稳定性同样会通过实验说明.

本文的内容组织如下，在第一节中我们将介绍一些在下面分析中会用到的基本概念和结论.同时我们还会在这一节简单地介绍下MM算法.而在第二节中我们将给出本文所提出的MEN-Sp模型，并构造两种算法来求解这个模型.在第三节中，我们将通过实验从稳定性和准确性两个方面验证算法的有效性.最后，在第四节中，我们将对本文进行简要的总结.

1 预备知识

在这一部分，我们将给出下面分析中要用到的一些基本定义结论和算法框架.

1.1 基本定义与性质

定义1：一个秩为r的矩阵X，其奇异值分解为

X=U∑VT,∑=Diag({σi(X),1≤i≤r}),对于任意的v≥0，加权奇异值收缩算子Dv(:,ω)可以表示为

Dv(X,ω)=UDiag(σi(X)-vωi)iVT,i=1,2,…,r.

其中对任意的a∈R，(·)+:=max(a,0)；ωi(i=1,2,…,r)是权向量ω的元素；σi(X),i=1,2,…,r是X的奇异值.

而文献[29]证明了加权奇异值收缩算子Dv(:,ω)是与加权核范数相关的近邻算子.

引理1：对于任意的v≥0，W=Diag(ω),Y∈Rm×n,加权奇异值收缩算子Dv(Y,W)是下面问题的最优解：

1.2 Majorization-minimization(MM)算法

为了解决非凸优化问题，本文引入MM算法[33].MM算法十分容易理解并且在生存分析、变量选择以及DNA序列分析等各个领域也有广泛的应用.MM算法的主要思想是通过用一系列的简单的凸优化问题来替代原始的复杂的非凸优化问题以达到简化问题的目的.假设J(x)是原始的非凸问题，而xk是J(x)最小值的估计值.基于这个估计值，MM算法需要先构造一个新的函数G(x,xk)，之后我们通过最小化G(x,xk)来得到xk+1.关于G(x,xk)的构造方法可以根据原始函数的形式来灵活选择，当然这个构造函数要满足以下的条件：

a：G(x,xk)需要比较容易求解，否则就没有任何意义了；

b：对于任意的x，G(x,xk)≥J(x)；

c：G(xk,xk)=J(xk).

由上述的函数构造方法，我们可以知道

J(xk+1)=G(xk+1,xk+1)=minG(xk+1,z) ≤G(xk+1,xK)=minG(x,xk) ≤G(xk,xk)=J(xk).

即J(xk+1)≤J(xk)，而此下降趋势使得MM算法有显著的数值稳定性.

用MM算法来最小化J(x)可以总结为以下几个步骤：

1) 令k=0.初始化x0；

2) 构造G(x,xk)使之满足：

(a)对任意的x，G(x,xk)≥J(x)；

(b)G(x,xk)=J(xk);

4) k=k+1，返回第2步；

2 MEN-Sp模型及求解算法

在这一部分，我们首先提出我们的基于Schatten p-norm最小化的矩阵弹性正则化模型，之后，给出两种不同的算法来求解这个模型.首先我们将给出此模型的整体估计量的形式，即损失函数和MEN-Sp惩罚项(Schatten p-norm和Frobenius范数结合)的极小化变量，而所谓的MEN-Sp惩罚项可以定义如下:

为了恢复原始矩阵M0，基于MEN-Sp惩罚项的矩阵弹性正则化可以写成如下形式:

(8)

以上模型就是我们本文中的主要优化模型MEN-Sp.为了方便表示，我们在下面的推导中假设X∈Rn×n,b∈Rs.

2.1 一种新的交替迭代算法

在这部分，我们构造一种新的交替迭代算法来优化模型(8).首先我们将(8)的模型变化为下面的形式：

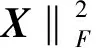
s.t. Y=X-AT(A(X)-b),

W=(σ(X)+ε0)p-1.

(9)

受文献[30]的启发，模型(9)可以通过以下三个步骤解决：

计算Xk+1：固定Xk和Yk，通过最小化P(X,Yk,Wk)得到Xk+1：

(10)

由引理1可知，上述问题的解可以表示为

计算Yk+1：固定Xk+1，计算Yk+1如下：

Yk+1=Xk+1-AT(A(Xk+1)-b).

计算Wk+1：固定Xk+1，计算Wk+1如下：

Wk+1=(σ(Xk+1)+ε0)p-1.交替迭代算法的完整计算流程总结在算法2.1中.

算法2.1：交替迭代算法

输入：线性算子A:Rm×n→Rs(s≪mn)，观测向量b∈Rs,p∈(0,1)，正则化参数λ,ε,ε0≥0，最大迭代次数为kmax，衰减系数为defac；

输出：恢复矩阵Xopt；

初始化：Y0=0,k=0,W0=0

For k=1:kmax

步骤1：计算Xk+1，；

步骤2：更新Y，Yk+1=Xk+1-AT(A(Xk+1)-b)；

步骤3：更新W，Wk+1=(σ(Xk+1)+ε0)p-1；

步骤4：如果收敛，Xopt=Xk+1.否则k=k+1,λ=defac×λ返回第二步.

2.2 基于MM算法的优化方法

在这一部分，我们将构造一个基于MM算法框架的算法来优化(8).由于MM算法通常用来解决基于向量的优化问题，所以我们先将原始问题转化为下面的等价形式：

(11)

这里x=vec(X)，A是A的矩阵形式.由于最小化J(x)比较困难，所以我们考虑J(x)的二次替代函数：

(12)

对上述方程的项重新整理后，G(x,xk)可以重新表示为

(13)

其中zk=xk+α-1AT(b-Axk).剔除掉其中与无关的常数项，等价于最小化下面的替代方程：

(14)

假设矩阵X有r个大于0的奇异值：σ1≥σ2≥…≥σr>0.一般情况下，对于X的奇异值分解X=U∑VT，下面性质成立：

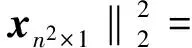
(15)

而通过对上述表达式进行微分运算可以很容易地得到解的形式.这里，我们省略掉简单的数学运算，最小化(15)得到的解为

(16)

基于上述的推导，基于MM算法框架的优化算法总结在算法2.2中.

算法2.2：基于MM算法的优化算法

输入：仿射矩阵A，常数α，正则化参数λ，ε最大循环次数kmax，衰减系数defac;

输出：Xopt；

初始化：X0=0∈Rm×n；

For k=1:kmax

步骤1：令zk=xk-1+α-1AT(b-Axk-1).将向量zk-1重新排列成矩阵Zk-1；

步骤2：SVD分解：Zk=U∑VT，其中∑是由σzk-1作为对角线元素组成的对角矩阵；

步骤3：得到Xk的奇异值如下所示

否则λ=defac×λ，返回第二步.

算法2.2的主要计算时间消耗是在第二步，也就是SVD分解.其他步骤的耗时基本上很少.对于大维数的矩阵恢复问题，我们可以使用PROPACK包来计算部分SVD分解来加速算法的运算速度，这样也会使我们的算法更加有效率.此外，MM算法还保证了算法2.2的收敛性.

3 实验结果与分析

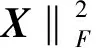
矩阵填充作为矩阵恢复的一个特殊案例，其在人脸识别、机器学习以及图像处理等方面也有着广泛应用.这里为例验证我们算法的有效性，我们拟解决下面的问题：

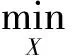
(17)

其中：Ω是势为s的随机子集，PΩ:Rm×n→Rm×n为一线性投影算子，即PΩ(Mij)=Mij,if(i,j)∈Ω,否则为0.模型(17)同样可以由以上两种优化算法进行求解.

图1 原始图片Figure 1 Original images

3.1 参数选择

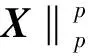
3.2 MEN-Sp的稳定性实验

正如我们在上面提到的，Lasso模型(ε=0)在预测值是高相关或者预测值的数量远远大于观测值时解会表现出不稳定性.再者，共线性也会严重削弱Lasso的恢复能力.因此,在这一部分我们将通过实验来说明我们的算法对于高相关矩阵的稳定性控制能力.而为了使实验结果更加有说服力，我们分别对随机人工矩阵和构造的低秩图片进行矩阵填充实验.其中随机人工矩阵的构造方法为:LRT,L,R为的矩阵并且矩阵元素是独立同分布的(i.i.d)，而构造图片“Strip”(265×100)是包含六个灰度值(0,50,100,10,200,250)的秩为1的图片.而为了选择一个合适的ε值，我们分别选取ε=0,ε=1e-7,ε=1e-6来进行对比.这三种模型分别表示为MEN-Sp0，MEN-Sp1和MEN-Sp2，本部分我们采用峰值信噪比(PSNR)来刻画恢复效果.

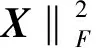
表1 人工数据十次恢复结果的标准差Table 1 Standard deviation for “synthetic data” with ten runs

表2 “Strip”十次恢复结果的标准差Table 2 Standard deviation for “Strip” with ten runs

图2显示了对“Strip”的随机十次填充效果.从图中可以容易看出，随着值的增大，恢复曲线趋于平稳，这就意味着标准差越小解越稳定，这与表2中的数据也是吻合的.总之，不管是从图中的视觉效果还是从表中的数据来看，MEN-Sp1和MEN-Sp2都要比MEN-Sp0稳定，而MEN-Sp2又比MEN-Sp1要稳定.从恢复效果上看，相对较大的值会影响恢复的准确率，也就是说的增加会增强稳定性但是也会引起PSNR值的减小，因此我们要选择一个合适的值来平衡稳定性和恢复效果.事实上从实验结果来看，我们倾向于选择，因为其对稳定性的控制更加有效并且与相比并没有较大的PSNR的损失，故在下一部分的参数设置中，我们选择作为最后一个正则化参数.

3.3 MEN-Sp正则化

为了突出我们的算法在测量值较少时的恢复效果，我们在本部分主要考虑元素缺失较多的情况.不同于上个部分，本节我们采用相对误差来刻画恢复效果：

我们将我们的算法MEN-Sp和对比算法MEN分别应用于自然图片“boat”和“Monarch”上，恢复效果图显示在图3中，图3的第一行是原始图片的降秩后效果，第二行为对降秩后的图片随机缺失掉60%的效果，算法MEN的恢复结果显示在第三行，我们的算法MEN-Sp的恢复结果显示在第四行.从视觉效果上也可以看出第四行比第三行的效果更好.相应的数值计算结果可以参考表3，从表中也可以看到，我们算法的恢复效果要远远优于MEN.值得注意的是，MEN的计算时间随着缺失元素的增多并没有大的波动，这是因为MEN在200次循环后并没有收敛到我们满意的状态，所以每次都要计算200次.相比之下，我们的算法的收敛性更快，这也是我们的基于MM算法框架的优势，比如说当缺失50%时，我们的算法在循环150次时就收敛到理想状态.尽管看上去我们的算法的时间要长，但这是因为在每次的循环中我们的算法都要进行大量的SVD分解.综合上述的因素来看，我们的MEN-Sp确实要优于MEN.

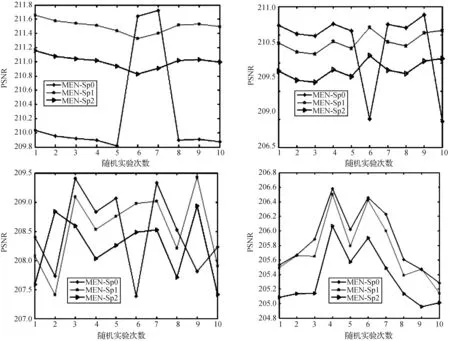
图2 在不同的缺失情况下MEN-SP 对“Strip”的恢复结果.Figure 2 Performance of the MEN-Sp algorithm on “Strip” for different randomly masked set.

图3 自然图片“boat”和“Monarch”恢复效果对比Figure 3 Comparisons in terms of the natural images “boat” and “Monarch” respectively

缺失程度/%恢复结果刻画方式boatMonarchMENMEN⁃SpMENMEN⁃Sp50相对误差0．00672．2442e⁃060．06894．7889e⁃05时间2410167760相对误差0．02811．2013e⁃050．13801．4889e⁃04时间24169713170相对误差0．06567．0862e⁃050．18870．1327时间24362612780相对误差0．12460．08520．27570．2572时间24466130

4 总结与展望

在低秩矩阵恢复研究领域，用核范数最小化来逼近秩函数这一传统方法虽然得到了广泛的应用，但是核范数最小化方法平等地对待每一个奇异值，这显然是不合理的.

[1] SREBRO N, RENNIE J, JAAKKOLA T S. Maximum-margin matrix factorization[C]// Advances in Neural Information Processing Systems. Granada: NIPS,2004:1329-1336.

[2] YE Jieping. Generalized low rank approximations of matrices[J]. Machine Learning,2005,61(1-3):167-191.

[3] SREBRO N, JAAKKOLA T. Weighted low-rank approximations[C]//Proceedings of the Twentieth International Conference on Machine Learning. Washington DC:AAAI Press,2003,3:720-727.

[4] ZHANG Chunjie, LIU Jing, TIAN Qi, et al. Image classification by non-negative sparse coding, low-rank and sparse decomposition[C]// Proc of IEEE Conf on Computer Vision and Pattern Recognition (CVPR). Colorado: IEEE,2011:1673-1680.

[5] MA Long, WANG Chunheng, XIAO Baihua, et al. Sparse representation for face recognition based on discriminative low-rank dictionary learning[C]// Proc of IEEE Conf on Computer Vision and Pattern Recognition. Rhode Island: IEEE,2012:2586-2593.

[6] SHASHUA A, HAZAN T. Non-negative tensor factorization with applications to statistics and computer vision[C]// Proc of the 22nd Int Conf on Machine Learning. Bonn: ACM,2005:792-799.

[7] BARTOLI A, GAY-BELLILE V, CASTELLANI U, et al. Coarse-to-fine low-rank structure-from-motion[C]// Proc of IEEE Conf on Computer Vision and Pattern Recognition. Anchorage: IEEE,2008:1-8.

[8] ZHANG Zhengdong, MATSUSHITA Y, MA Yi. Camera calibration with lens distortion from low-rank textures[C]// Proc of IEEE Conf on Computer Vision and Pattern Recognition. Colorado: IEEE,2011:2321-2328.

[9] SHEN Xiaohui, WU Ying. A unified approach to salient object detection via low rank matrix recovery[C]// Proc of IEEE Conf on Computer Vision and Pattern Recognition. Rhode Island: IEEE,2012:853-860.

[10] LIU Guangcan, LIN Zhouchen, YU Yong. Robust subspace segmentation by low-rank representation[C]// Proc of the 27th Int Conf on machine learning (ICML-10). Haifa: IMLS,2010:663-670.

[11] TAKáCS G, PILáSZY I, NéMETH B, et al. Matrix factorization and neighbor based algorithms for the netflix prize problem[C]// Proc of the 2008 ACM Conf on Recommender systems. Lausanne: ACM,2008:267-274.

[12] BENNETT J, LANNING S. The netflix prize[C]// Proc of KDD Cup and Workshop. New York: ACM,2007,3-6.

[13] BELL R M, KOREN Y. Lessons from the Netflix prize challenge[J]. ACM SIGKDD Explorations Newsletter,2007,9(2):75-79.

[14] CANDES E J. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique,2008,346(9):589-592.

[15] DONOHO D L. Compressed sensing[J]. IEEE Trans on Information Theory,2006,52(4):1289-1306.

[16] CANDèS E J, RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational mathematics,2009,9(6):717-772.

[17] CANDèS E J, TAO T. The power of convex relaxation: Near-optimal matrix completion[J]. IEEE Trans on Information Theory,2010,56(5):2053-2080.

[18] FAZEL M. Matrix rank minimization with applications[D]. Palo Alto: Stanford University,2002.

[19] MAZUMDER R, HASTIE T, TIBSHIRANI R. Spectral regularization algorithms for learning large incomplete matrices[J]. Journal of Machine Learning Research,2010,11(11):2287-2322.

[20] TOH K C, YUN S. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems[J]. Pacific Journal of Optimization,2010,6(3):615-640.

[21] FUKUSHIMA M. Application of the alternating direction method of multipliers to separable convex programming problems[J]. Computational Optimization and Applications,1992,1(1):93-111.

[22] MA Shiqian, GOLDFARB D, CHEN Lifeng. Fixed point and Bregman iterative methods for matrix rank minimization[J]. Mathematical Programming,2011,128(1-2):321-353.

[23] LI Hong, CHEN Na, LI Luoqing. Error analysis for matrix elastic-net regularization algorithms[J]. IEEE Trans on Neural Networks and Learning Systems,2012,23(5):737-748.

[24] HU Yao, ZHANG Debing, YE Jieping, et al. Fast and accurate matrix completion via truncated nuclear norm regularization[J]. IEEE Trans on Pattern Analysis and Machine Intelligence,2013,35(9):2117-2130.

[25] ZHANG Debing, HU Yao, YE Jieping, et al. Matrix completion by truncated nuclear norm regularization[C]//Proc of IEEE Conf on Computer Vision and Pattern Recognition. Rhode Island: IEEE,2012:2192-2199.

[26] 陈甲英,赵建伟,曹飞龙.一种新的鲁棒主成分分析方法及其应用[J].中国计量学院学报,2016,27(1):113-120. CHEN Jiaying, ZHAO Jianwei, CAO Feilong. A novel robust principal component analysis method and its applications[J]. Journal of China Jiliang University,2016,27(1):113-120.

[27] HU Yao, JIN Zhongming, SHI Yi, et al. Large scale multi-class classification with truncated nuclear norm regularization[J]. Neurocomputing,2015,148:310-317.

[28] MAJUMDAR A, WARD R K. An algorithm for sparse MRI reconstruction by Schatten p-norm minimization[J]. Magnetic resonance imaging,2011,29(3):408-417.

[29] NIE Feiping, HUANG Heng, DING C H Q. Low-Rank Matrix Recovery via Efficient Schatten p-Norm Minimization[C]//Proc of the 26th Conf on Artificial Intelligence. Toronto: AAAI Press,2012:655-661.

[30] LI Yufan, ZHANG Yanjiao, HUANG Zhenghai. A reweighted nuclear norm minimization algorithm for low rank matrix recovery[J]. Journal of Computational and Applied Mathematics,2014,263:338-350.

[31] ZOU Hui, HASTIE T. Regularization and variable selection via the elastic net[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology),2005,67(2):301-320.

[32] GAIFFAS S, LECUé G. Sharp oracle inequalities for high-dimensional matrix prediction[J]. IEEE Trans on Information Theory,2011,57(10):6942-6957.

[33] HUNTER D R, LANGE K. A tutorial on MM algorithms[J]. The American Statist Ician,2004,58(1):30-37.

Regularization algorithm for matrix recovery based on reweighted nuclear norm

ZHANG Yanan, ZHAO Jianwei, CAO Feilong

(College of Sciences, China Jiliang University, Hangzhou 310018, China)

Whether in the field of compressive sensing or matrix recovery, the elastic-net regularization has attracted wide attention. It is a successful approach in statistical modeling which can avoid large variations which always occur in estimating complex models. In order to improve the defect of the nuclear norm minimization which requires more measurement for exact recovery of low rank solution and enhance the stability of the solution, we proposed a new matrix elastic-net regularization method based on Schattenp-norm minimization(MEN-Sp). To minimize this no-convex model, alternating iterative algorithm and MM algorithm were adopted. And the superiority of the MEN-Sp regularization algorithm for recovering the matrix with fewer measurement was also proved by the simulation experiment.

matrix recovery; elastic-net regularization; Schattenp-norm; alternate iterating algorithm; MM algorithm

2096-2835(2016)04-0471-09

10.3969/j.issn.2096-2835.2016.04.020

2016-09-27 《中国计量大学学报》网址：zgjl.cbpt.cnki.net

国家自然科学基金资助项目(No.61672477,61571410,91330118).

TP391

A