一种测试数据分块纵向相容的编码压缩方案

李建新，吴孝银

宿州学院智能信息处理实验室，安徽宿州，234000

一种测试数据分块纵向相容的编码压缩方案

李建新，吴孝银

宿州学院智能信息处理实验室，安徽宿州，234000

为有效降低集成电路的测试数据量,设计了一种测试数据分块纵向相容的编码压缩和解压方案。将原始测试集中的每一测试向量以固定位数分块，然后将顺序号相同的数据块归为一列，根据每一列数据块间的相关性，将长的数据块用短的标记码表示，从而实现测试数据的压缩,进而设计了与该编码方案相应的解压结构。研究表明：该方案与同类方案相比有较高的编码压缩率,而且解压过程简单易行。

标记编码；更新；纵向相容；#运算；∩运算

随着集成电路制造工艺水平的不断提高,单个芯片上集成的晶体管数量呈指数规律增长。尤其是片上系统(System-on-a-Chip,SoC)的出现，芯片中集成了大量的IP核，完成测试的数据量迅速增长,导致自动测试设备存储容量不足、传输带宽受限、测试时间增长,实施测试变得越来越困难，测试成本不断提高[1]。因此，研究先进的集成电路测试方法,以减少测试数据传输量，降低测试成本具有重要的理论和实用价值。

测试数据编码压缩技术可有效解决上述问题。该技术的总体思路是将原始测试数据经编码压缩后存储在ATE上，传输的数据量得以降低，在待测芯片中嵌入相应的解压电路，对从ATE传过来的压缩数据进行解压还原，再将还原后的测试数据施加给待测电路[1]。常见的编码压缩技术有基于数据块的编码压缩、基于数据流的编码压缩及基于重播种的编码压缩技术三类。基于数据块的编码又可分为统计编码和相容压缩标记编码，其中，前者有Huffman编码[2]，它是典型的统计编码；后者有相容压缩标记编码，如数据块前向相容的标记码[3]、分组合并的索引编码[4]等。基于数据流游程的编码有Glomb编码[5]、FDR编码[6]以及交替码[7]等。基于重播种的编码压缩技术有LFSR重播种技术[8]和折叠计数器重播种技术[9]。

本文提出一种测试数据分块纵向相容的编码压缩方案。该方案讲述的是基于数据块相容的标记码压缩技术，能在提高编码压缩率的同时，简化解压还原电路。

1 两种相关运算的回顾

在文献[4]中，曾引入两种位运算符：#运算及∩运算，为便于利用,现作一简单回顾。一位#运算和∩运算规则分别如表1和表2所示。

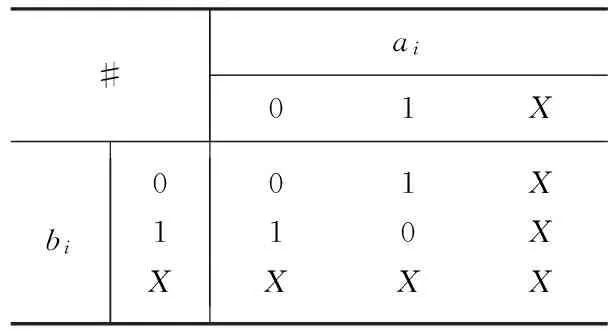
表1 #运算表

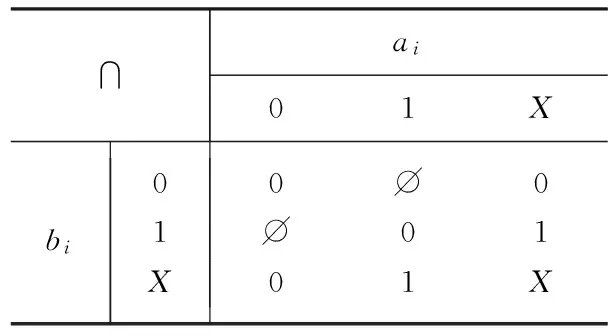
表2 ∩运算表

根据表1的#运算规则，可引入两等数位测试模式间相关性的有关概念。假设测试模式a=a1a2…an-1an,ai∈{0,1,x}，b=b1b2…bn-1bn，bi∈{0,1,x}，其中x为{0,1}中的任意值,将a、b的对应位按表1进行“#”操作，若运算结果各位全部是0或x，则称模式a与b相容；若运算结果各位全部是1或x，则称模式a与b反相相容；二者统称为模式相关。

假定有如下3个等数位的测试模式：a=01X0XX01，b=X11X00X1，c=1X0110X0，若按表1中#运算法，将a、b、c三个模式两两进行位运算，则有：a#b=X0XXXXX0，a#c=1XX1XXX1，b#c=XX1X10X1。从运算结果可算出，模式a与b相容，a与c反相相容，b与c不相关。

根据表2中的“∩”运算，可将相关的两测试模式合并。对于互为反相相容的两种模式，可将其中之一反相后，再与另一模式作“∩”运算。如在上例中，a∩b=01100001，将c模式反相得～c=0X1001X1，a∩～c=01100101。可见，运用“∩”运算可使测试模式中的确定位增加。

2 纵向相容的标记编码方法

为便于描述，现举一示例阐述编码方法。某测试集TD由4个测试模式组成，如表3所示，每个测试模式位数均为15位。编码前，先将测试集中的每个测试模式划分成定长为K位的分块，如果测试模式的总位数不是块长K的整倍数，不足的位数则用无关位X填补，使其为K的整数倍。本例中取块长K=8，每个模式被划分为二块，第二块不足8位，补充一位无关位(表中斜体X)。为便于表述，用Cij表示第i个测试模式的第j个测试分块，如表3中C11=01X101XX，C32=0X010X1X。

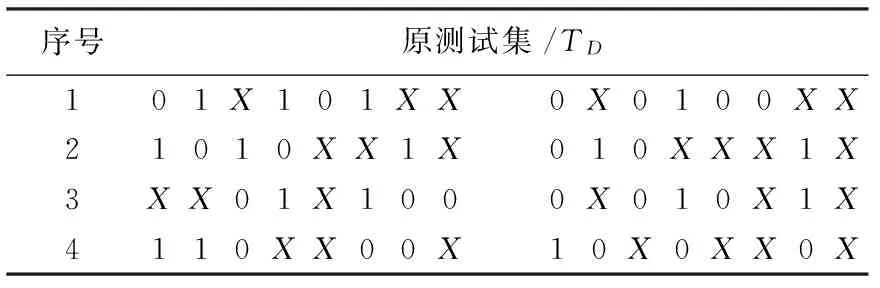
表3 本编码方案实例

编码总体思路为：取参考模式，对测试集的每一列分块沿纵向按从上至下的顺序进行“#”运算，采用“#”运算结果，进行标记编码分类，同时采用“∩”运算不断更新参考模式。具体方法为：对每一列的测试模块，取某一K位参考模块R0，按从上到下的纵向顺序，从第一个测试模块开始依次按位进行“#”运算，根据运算结果判断相关性并进行标记编码。若测试模块与参考模块相容，则将该测试模块标记编码为“0”，并将参考模块与该模块按位进行“∩”运算，以增加其中的确定位，再将“∩”运算结果作为下一个测试模块的参考模块；若测试模块与参考模块反相相容，则将该测试模块标记编码为“10”，并将该测试模块反相后与参考模块按位作“∩”运算，再将“∩”运算结果作为下一个测试模块的参考模块；若测试模块与参考模块既不相容又不反相相容，即不相关，则采用在该测试分块前加“11”进行编码标记，同时将该测试分块作为新的参考模块对下一个测试分块进行运算编码。因可采用复位的办法将集成电路内部各位触发器初始化为全0，故每一列测试分块的初始参考模块R0可取K位0，并按上述方法从第一个测试分块进行运算编码。

现以表3中的第一列测试数据块为例作具体描述。取8位初始参考模块R0为00000000，与C11(01X101XX)按位作“#”运算，由“#”运算规则，R0#C11=01X101XX，显然二者不相关，故C11被编码为：1101X101XX，参考模块被更新为新的参考模块R1=R0∩C11=01X101XX；进而将R1与C21(1010XX1X)按位作“#”运算，R1#C21=11X1XXXX，二者反相相容，故C21被编码为“10”，然后将C21反相为～C21=0101XX0X，新的参考模块更新为R2=R1∩～C21=0101010X；将R2与C31(XX01X100)按位作“#”运算，R2#C31=XX00X00X，二者相容，故C31被编码为“0”，然后将参考模块更新为R3=R2∩C31=01010100；将R3与C41：110XX00X按位“#”运算，R3#C41=100XX10X，二者既不相容也不反相相容，故C41被编码为：11110XX00X，参考模块更新为R4=C41=110XX00X。

对表3中的第二组测试模块也可采用上述同样方法进行编码和更新。对整个测试集中每个测试集的编码结果如表4所示，其中的“-”不占有数据位，只是为编码结果规整而设的。将表4左右数据对比可看出，原测试集TD的总位数为60，编码后总位数为37，压缩了23位。

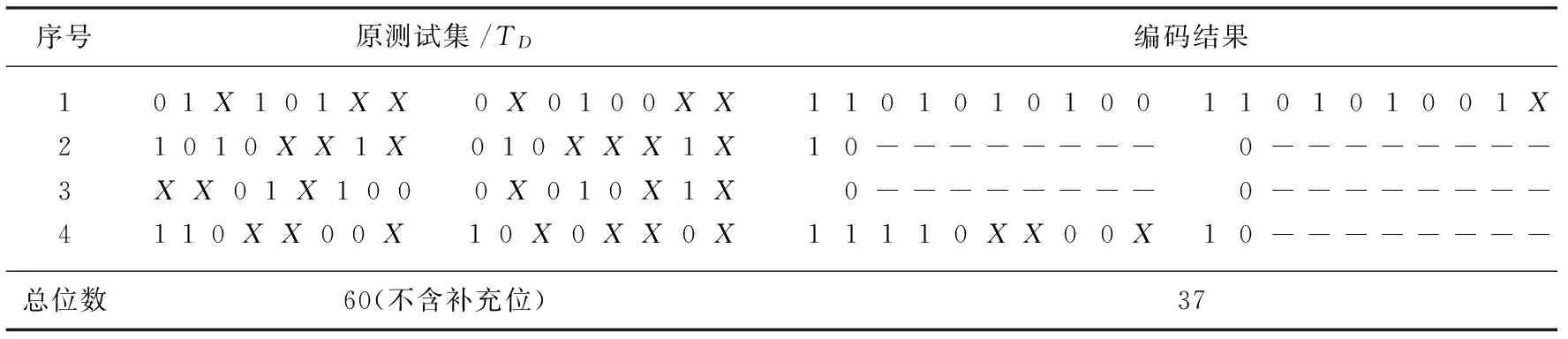
表4 对原测试集的运算编码结果

3 解压结构及过程分析

编码的目的是实现测试数据的压缩，减少数据量，缩短测试传输时间，但压缩后的数据是不能直接用于电路测试的，要实现有效测试，尚需在芯片中设计相应的解压电路，将原测试集中的所有确定位进行还原。

不同的编码方案应对应不同的解压电路。本方案的解压结构如图1所示，其中，有限状态机(Finite State Machine,FSM)是解压结构的核心，K位循环扫描移位寄存器(Cycle Scan shift Register,CSR)用于存放和更新各列K位参考模块,K进制计数器用于控制data_out输出和CSR移位的位数，MUX1、MUX2均为2选1的数据选择器，MUX1受select1控制，用于数据输出选择，MUX2受select2控制，用于返回参考模块的选择,CUT(Chip Under Test,CUT)为被测芯片。

图1 解压结构

解压过程分析：

Step1 初始化，enable使能允许，CSR各位清零，K进制计数器置位。

Step2 bit_in输入一位数据，若为“0”，转入Step3，若为“1”，转入Step4。

Step3 从data_out端连续输出K位0，同时，CSR内的参考模块右移K位，两路数据经异或门按位作异或运算，由于任何数据与0异或仍保持不变，故运算后仍为CSR内的原数据。此时，select1、select2分别控制MUX1、MUX2均选0端有效，从MUX1输出的数据即为CSR内的原数据，该数据一方面进入CUT进行测试，另一方面返回CSR继续作为下一个参考模块。然后转入Step7。

Step4 bit_in再输入一位数据，若为“0”，转入Step5，若为“1”，转入Step6。

Step5 从 Data_out端连续输出K位1，同时，CSR内的参考模块右移K位，两路数据经异或门按位作异或运算，由于任何数据与1异或即反相，故运算后即将参考模块按位取反，由select1控制MUX1选0端有效，由select2控制MUX2选1端有效，从MUX1输出的数据即为参考模块的反相数据，也就将原测模块中确定位进行了还原，该数据一方面进入CUT实现测试，另一方面经反相后返回CSR继续作为下一个参考模块。然后转入Step7。

Step6 将bit_in当前位置后一位开始的连续K位数据从Data_out端输出，由select1控制MUX1选1端有效，由select2控制MUX2选0端有效，这样从Data_out输出的K位数据将原封不动地经MUX1输出，进入CUT进行测试的同时,返回CSR继续作为新的参考模块,表明这组K位输出数据与CSR中的参考模块不相关。然后进入Step7。在该步骤中，CSR中的参考模块数据右移K位后与Data_out输出的K位数据也存在异或情况,但异或的结果不被选用,自动舍弃。

Step7 循环重复Step2到Step6。

在上述解压电路中，K进制减1计数器控制CSR右移的位数及Data_out输出数据的位数。K进制计数器的减1计数功能由dec信号控制，计数结束时，rs有效，K进制减1计数器被重新赋初值K，valid信号控制CSR是否右移。

对表3所示的编码实例解压还原后的结果如表5中第4列所示(TE)，将其与第二列中原测试集TD比较可知，二者完全相容。

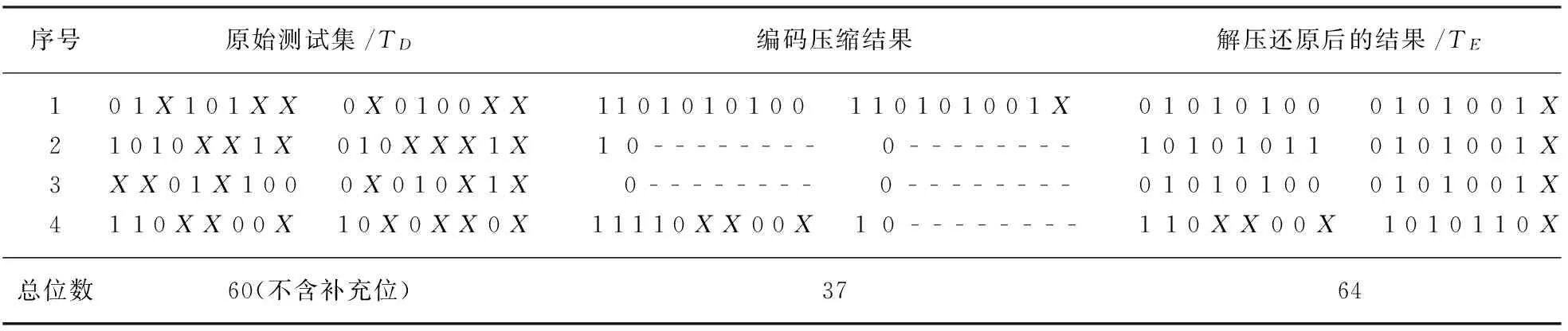
表5 对表4编码解压还原结果

4 结果与分析

对于本方案的编码压缩效果，选用ISCAS-89基准电路几个典型的时序电路作为实验对象，通过对Mintest测试向量集压缩进行验证。实验过程是对每一种电路取不同的块长进行纵向相容标记编码压缩，分别得出对应的压缩率，实验结果如表6。

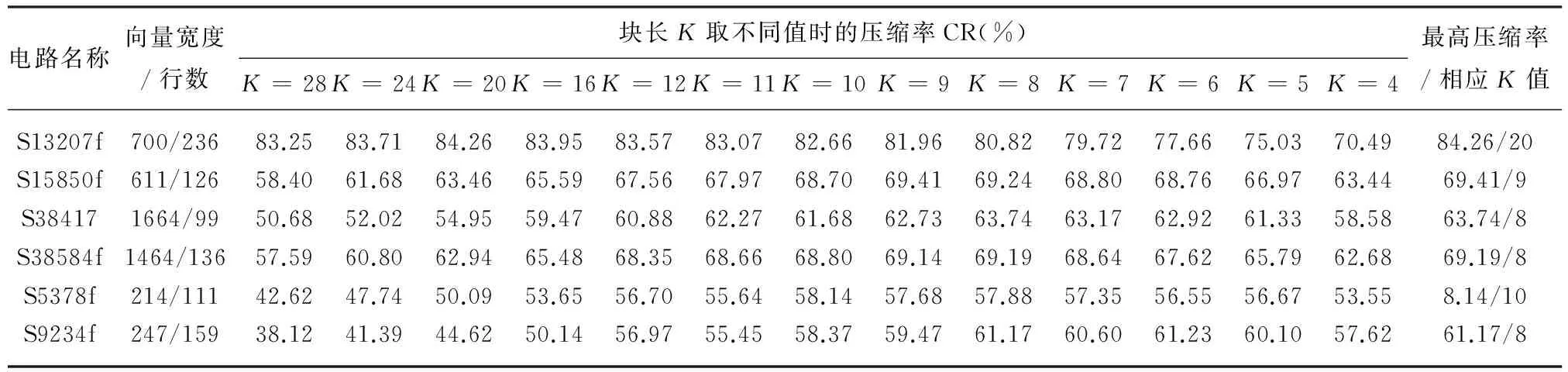
表6 块长K取不同值时对各测试电路测试的压缩率

测试数据压缩,TD为原测试集数据量，TE为编码压缩后的测试集数据量。

从表6可看出，对每一种测试电路的测试集进行纵向相容压缩，随着K值的变化，压缩率总会在某一种K值附近出现最大值拐点，即压缩率与块长间呈类抛物线关系。这是由于块长较短时，块数较多，相应的编码码字也多，限制了压缩率，块长较长时，块数虽少，但数据块间的相关性降低，从而也限制了压缩率，故二者之间类抛物线关系具有客观合理性。因此，为提高该方案的编码压缩率，须根据不同的测试集选取合适的块长。

将表6中各测试电路对应的最高压缩率与其他类似方案进行比较,结果如表7所示，可以看出，本文方案压缩率相对较高。

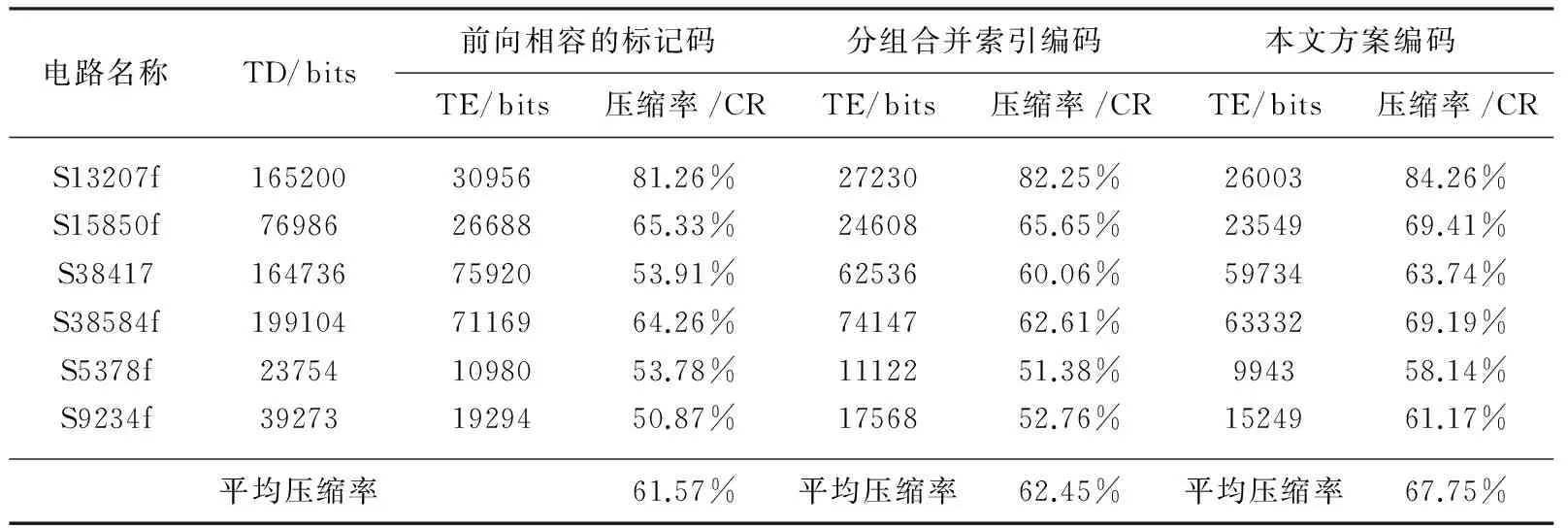
表7 本文方案与其他编码方案的压缩率比较

5 结束语

本文通过引入两种特殊的位逻辑运算,举例说明了测试数据分块纵向相容的编码压缩方法，设计了对应的解压还原电路，分步解析了其解压过程。该方案编码方法巧妙，解压过程流畅,实验证明,该方案与同类方案相比，能有效地提高编码压缩率。而且由于方案采用横向分块纵向编码，解压电路的CSR长度与分块块长相同，长度相对较短，故所需要的硬件不多，开销不会太大。

[1]时万春，张东，魏道政，等．现代集成电路测试电路测试技术[M]．北京：化学工业出版社，2006:157-160

[2]Jas A,Ghosh-Dastidar J,Mom-Eng N,et al.An efficient test vector compression scheme using selective Huffman coding[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2003,22(6):797-806

[3]欧阳一鸣，肖祝红，梁华国．数据块前向相容标记码的测试数据压缩方法[J]．计算机辅助设计与图形学学报，2007，19(8)：986-990

[4]李建新，梁华国，陶珏辉．基于测试数据分组合并的索引编码压缩方案[J]．计算机工程，2010，36(11)：265-267

[5]Chandra A,Chakrabarty K.System-on-a-chip test-data compression and decompression architectures based on Golomb codes[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2001,20(3):355-368

[6]Chandra A,Chakrabarty K.Test data compression and test resource partitioning for system-on-a-chip using frequency-directed run-length(FDR) codes[J].IEEE Transactions on Computers,2003,52(8):1076-1088

[7]梁华国，蒋翠云．基于交替与连续长度码的有效测试数据压缩和解压[J]．计算机学报，2004，27(4)：548-554

[8]Lien W C,Lee K J,Hsieh T Y,et al.Efficient LFSR Reseeding Based on Internal-Response Feedback[J].J Electron Test,2014,30:673-685

[9]梁华国，海伦布昂特，冯特利希.一种基于折叠计数器重新播种的确定自测试方案[J]．计算机研究与发展，2001，38(8)：931-938

(责任编辑：汪材印)

10.3969/j.issn.1673-2006.2016.03.029

2016-01-12

安徽省教育厅自然科学研究项目(KJ2014ZD31)；安徽省教育厅省级教学研究项目(2012jyxm545)；宿州学院科研平台开放课题(2011YKF09)；宿州学院优秀青年人才资助项目(2014XQNRL006)。

李建新(1971-)，安徽萧县人，硕士,高级实验师，主要研究方向：SOC故障诊断与测试。

TN407

A

1673-2006(2016)03-0115-04