电梯超载保护装置检测新法

■文/胡胜江 陈建伟 徐 涛 庞 涛

电梯超载保护装置检测新法

■文/胡胜江 陈建伟 徐 涛 庞 涛

运用有限元仿真软件Workbench分析了不同载荷时轿底中心与下横梁之间距离的变化规律，提出了以小载荷时的距离变化量推算大载荷时的距离变化量，进而检测电梯超载保护功能是否有效的方法。模型及试验数据表明，采用该方法对超载保护装置进行检测与常规的加载试验基本等效，为研制该类超载保护装置的检测仪提供了理论依据，使得检验时无需搬运大量的砝码，提高了检测效率，降低了检测成本和劳动强度。

超载保护装置是电梯的重要安全装置之一，它可以防止电梯超载导致制动力不足而引起轿厢加速坠落等恶性事故，保护电梯内乘客与货物的安全。国家质检总局规定，对新安装及定期检验的电梯都应进行加载试验，验证超载保护装置的功能是否正常。加载试验的具体方法为：向空轿厢内均匀放置与超载载荷（超载载荷根据电梯的额定载荷确定）等重量的砝码，查看超载保护装置的动作情况。如果此时正好动作，表示其符合标准要求；提前动作会导致电梯过早提示超载，降低使用效率；不动作会导致电梯超载运行，形成严重的安全隐患。由于砝码租借、运输及人工费用高，检验花费时间长，实践过程中几乎没有单位会在电梯定期检验时进行加载试验，从而导致超载保护装置失效后不能及时被发现和处理，影响电梯的正常运行及安全性。

电梯超载保护装置的超载信号采集器通常有两种安装方式：一种是安装在绳头组的端部，检测绳头组受力大小或弹簧受力变形量；另一种是安装在轿厢的底部，检测轿底与下横梁之间距离的变化量，此时在轿底两侧都装有减震垫。

电梯轿底安装的减震垫一般有两种：一种是线性减震垫，其变形量与所受压力成正比，主要是弹簧；另一种是非线性减震垫，其变形量与所受压力不成正比，主要是橡胶。本文针对超载信号采集器安装在轿底且安装线性减震垫的情况，提出了一种无需加载规定载荷的砝码即可对超载保护装置进行检测的方法，为研制电梯超载保护装置检测仪提供理论依据。

方法的提出

以一种常见的电梯超载信号采集器为例说明其工作原理（见图1）。为超载信号采集工作原理图，图中上横梁2、立柱5和下横梁8等通过螺栓刚性联接组成轿厢架，悬挂于曳引钢丝绳1的下方；轿顶3、轿壁4和轿底6等通过螺栓刚性联接组成轿厢；在轿厢与轿厢架之间安装减震垫7；磁钢9安装在轿底6的中心位置；支架10安装在下横梁8的上面，霍尔接近开关11安装在支架10上，其位置处于磁钢9的正下方，与磁钢之间的距离可以调节。轿厢承受载荷后，轿底6将会受压下凹，减震垫7被压缩，磁钢9与霍尔接近开关11之间的距离将会减小，载荷达到一定值时霍尔接近开关11就会发出报警信号。

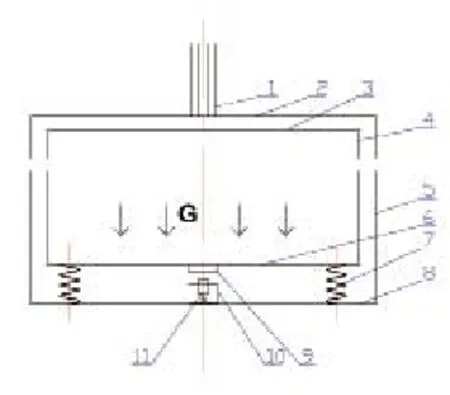
图1 电梯超载信号采集原

在做常规加载试验时，向空轿厢内均匀放置该电梯对应的超载载荷M，相对于空载时霍尔接近开关11与磁钢9的超载距离变化量为Y，平稳后调整霍尔接近开关11与磁钢9之间的距离，使霍尔接近开关11刚好动作，此为临界点，并在该位置将霍尔开关固定。经超载试验调整过的电梯在使用过程中，当轿厢内的载荷达到超载载荷M时，超载保护装置即会动作，向电梯中控系统发出超载报警信号。

假定轿厢内均匀加载小载荷X时，霍尔接近开关11与磁钢9的距离变化量为Z。如果存在一种函数关系，可以根据X和Z推算当轿厢均匀加载超载载荷M时霍尔接近开关11与磁钢9的距离变化量Y，那么在轿厢空载时将霍尔接近开关11向磁钢9方向移动距离Y，查看霍尔接近开关是否处于临界点，如果是，则认为超载保护装置功能有效；如果不是，则应上调霍尔接近开关11找到临界点并固定。此后，如果向轿内均匀加载超载载荷M，则超载保护装置应动作。可以看出，采用这种方法检测或调整超载保护装置时，无需对轿厢加载超载载荷M。

公式的提出

假设Z与X之间存在一定的函数关系：

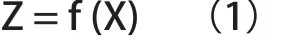
一、Z与X之间函数关系确定

依据电梯设计图纸对额定载荷为1000kg的电梯轿厢及轿厢架建立数学模型（见图2）。其中轿厢内尺寸为常见的1.6m×1.5m，轿厢及轿厢架等结构件材料为Q235钢板，多个减震垫分布于轿底与轿厢架之间的左、右两侧，列出模型的主要参数（见表1）。通过有限元方法分析（1）式中Z与X之间的函数关系。

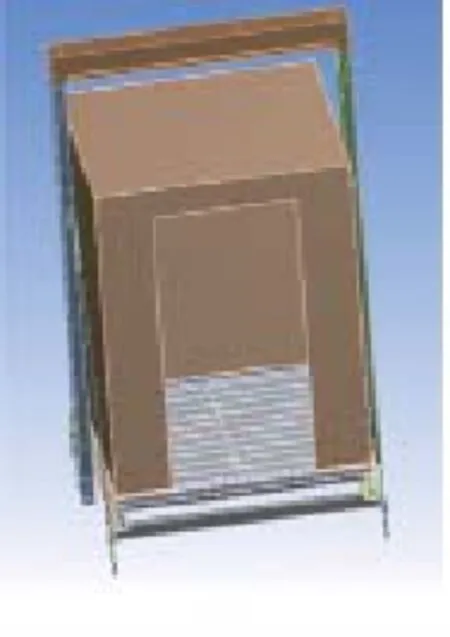
图2 轿厢及轿厢架数学模

利用有限元软件Workbench 对模型进行分析，共设置515420个节点、309232个单元，以上横梁为支撑，在轿厢加载试验块模拟现场加载砝码的情况（见图3）。通过改变模型中试验块的重量来改变载荷X，记录轿底中心与下横梁之间的距离变化量Z，得到X与Z的关系（见图4）。

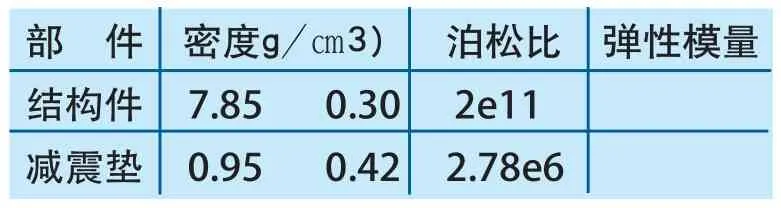
表1 模型的材料参数

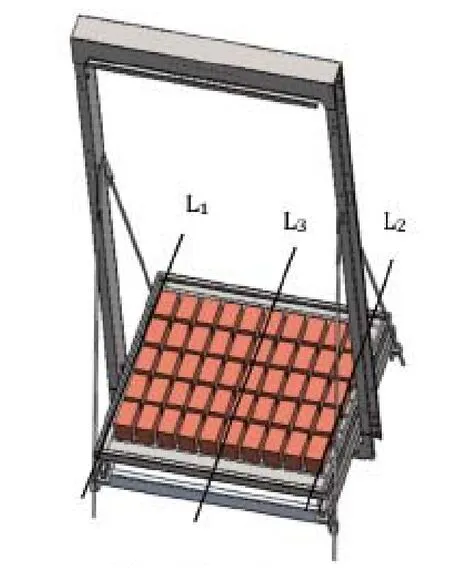
图3 轿厢加载模型

从图4可以看出，在轿厢均匀加载条件下，载荷X与距离变化量Z基本成线性关系。且当X=M时，Z=Y，则存在关系式：

当载荷X及其距离变化量Z已知时，超载距离变化量Y则可表示为：

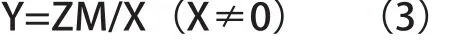
以上计算要求轿厢及轿厢架在超载条件下只发生弹性变形，在去掉载荷后变形恢复到空载水平。以表1的模型材料参数通过有限元分析，当电梯超载时各结构件中最大应力为112MPa，远低于Q235的屈服应力235MPa，所以轿厢及轿厢架在该条件下只发生了弹性变形。

为了便于携带和检测，载荷X不宜过大，一般取50kg左右，例如采用50块、每块重量为1kg的试验块在轿内均布，使用仪器检测距离变化量Z，通过公式（3）计算得到Y，再往磁钢方向移动霍尔接近开关Y的距离，根据超载保护装置的动作情况判断其功能是否有效或进行调整。

上述方法虽然可行，但在实际操作中试验块过小、数量太多，会使检测工作趋于繁琐，为此提出一种间接方式检测距离变化量Z以代替均匀加载的检测方式。

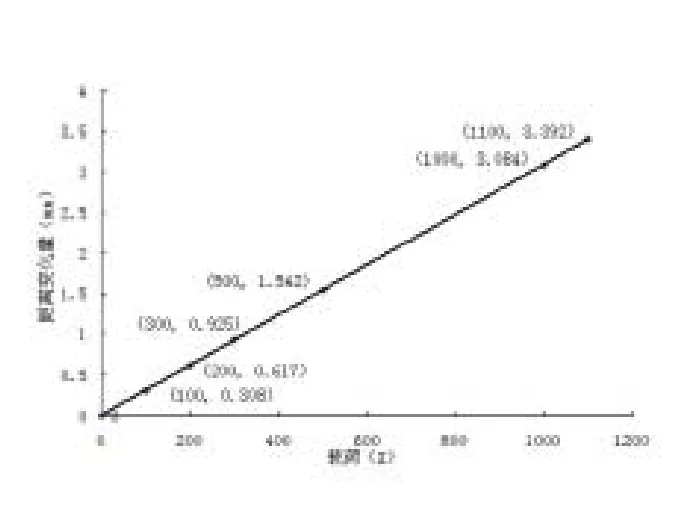
图4 载荷X与距离变化量Z的关系

将Z分解成加载后减震垫的变形量与轿底的变形量之和，并对这两部分分别进行讨论，设前者为Z1，后者为Z2，即：

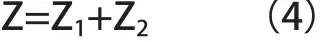
二、Z1的检测方法

轿底减震垫处的空间狭小，检测距离变化量的仪器安装困难，不便在该位置测量Z1。如图3模型中的线L1、L2所示，在轿厢左右两侧紧贴轿厢壁，从内至外各均匀加载25kg载荷。通过有限元分析可知，这种加载方式与轿厢均匀加载50kg载荷时减震垫的压缩量是相同的，而且压缩量Z1与所加载荷成线性关系。

试验测得，以上左右两侧加载的模型相比于空载时，轿厢中心位置下降量为0.1447mm，减震垫的压缩量为0.1438mm，前者相比于后者的误差为0.6%，表明在该加载条件下，以检测轿底中心位置距离变化量来代替减震垫的压缩量Z1误差非常小，对检测精度产生影响在允许范围之内。

设空载时轿底中心与下横梁的距离为T1，以上述方式加载后该距离为T2，则：

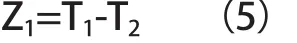
将（4）、（5）式代入（3）式得：

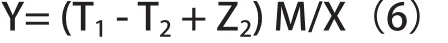
三、Z2的检测方法

在载荷均布的条件下，Z、Z1均为线性变化，则Z2也为线性变化。将轿厢视作安装在减震垫上的简支梁，轿厢的宽度即为简支梁的跨度，对于中心点的挠度，在轿厢内均匀加载等同于简支梁上均布载荷；在轿厢中心位置从内至外线性施加载荷（如图3中线L3所示）等同于简支梁上中心位置集中加载。通过材料力学[9]的相关公式可得到，在不考虑减震垫变形的条件下，简支梁上均布线性载荷q时，中间位置的挠度为：

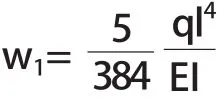
其中E为弹性模量，I为截面惯性矩，l为简支梁跨度；简支梁中心位置加载载荷P时，中间位置的挠度为：

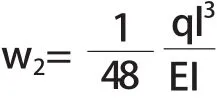
在同一模型中，当ql=P，即均布载荷等于集中载荷时，存在：

在轿厢中间位置从内至外线性加载载荷X，在轿底中心位置与下横梁的距离为T3，考虑此时减震垫变形后可得：

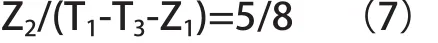
整理得：

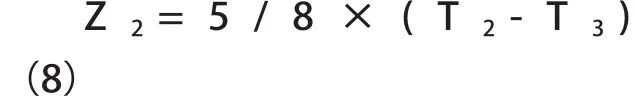
将（8）式代入（6）式可得：

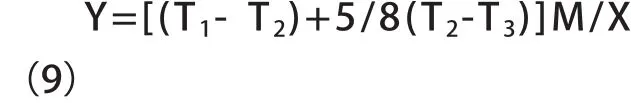
上式中M、X为已知量，T1、T2、T3为测量值，因此，根据（9）式即可计算出超载距离变化量Y。

公式的验证

将（9）式计算值Y与模型中的分析结果及实际检测数据进行对比验证，对（3）式在现场检测中进行验证。

一、（9）式模型验证

依据电梯图纸建立了三种常见额定载荷的轿厢模型，通过不同的轿厢尺寸、整体刚度及减震垫刚度等，验证（9）式的正确性及通用性，对比数据从模型中取值，见表2。表中T1、T2、T3、Y如前文中定义，X为加载载荷，T4指轿厢均布超载载荷M时轿底中心与下横梁的距离，T4-T1为超载时轿底中心与下横梁的距离变化量Y1，作为计算相对误差的真值，(9）式计算值Y与真值Y1之间的相对误差计算方法为：

从表2中可以看出，(9）式计算值Y与模型分析值Y1的相对误差较小，相符度较高。

二、（9）式现场验证

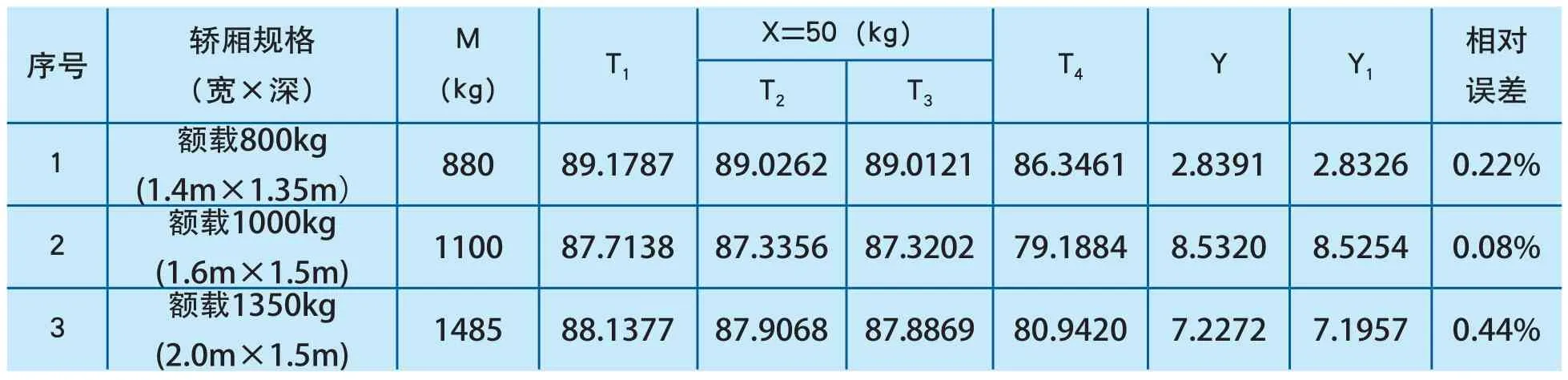
表2 （9）式计算值与模型分析数据对比

表3为现场加载试验的检测数据与（9）式计算值Y的对比。试验方法为：在空载时将千分表固定在下横梁上，表头紧贴轿底中心位置，读取数据T5；载荷X分成不同长度的试验块若干，组合使用以满足不同轿厢尺寸的要求。如图3中L1、L2所示位置，紧贴轿厢左右两侧的轿壁从里至外加载X/2载荷，读取数据T6；再将载荷X在轿厢中间位置从里至外加载，如图3中L3所示，读取数据T7。根据以上对于T1～T6的定义可知，读取的距离量T4～T6和（9）式中的距离量T1～T3之间存在如下关系：

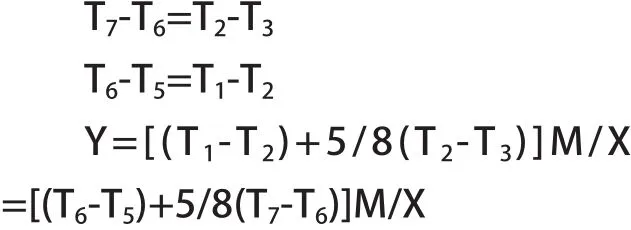
代入相应数据即可得到Y值。

清空轿厢，然后均布超载载荷M，读取数据T8，T8-T5就是现场轿厢均布超载载荷时轿底中心与下横梁的距离变化量Y2，作为计算相对误差的真值，(9）式计算值Y与真值Y2之间的相对误差计算方法为:

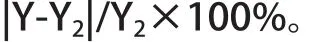
由于现场因素的影响，表3相对误差大于表2的相对误差，但均在5%以内，满足超载保护装置安全性能的检测要求。

三、（3）式现场验证

表4为现场加载试验的检测数据与（3）式计算值Y的对比，试验方法为：制作50个试验块，每块重量为1kg，载荷X=50kg；在空载时将千分表固定在下横梁上，表头紧贴轿底中心位置，读取数据T9；将50个试验块均布在轿厢内，读取数据为T10，则该载荷下距离变化量Z=T10-T9；清空轿厢，然后均布超载载荷M，读取数据T11，T11-T9为现场轿厢均布超载载荷时轿底中心与下横梁的距离变化量Y3，作为计算相对误差的真值，（3）式计算值Y与真值Y3之间的相对误差计算方法为：|Y-Y3|/Y3×100%。

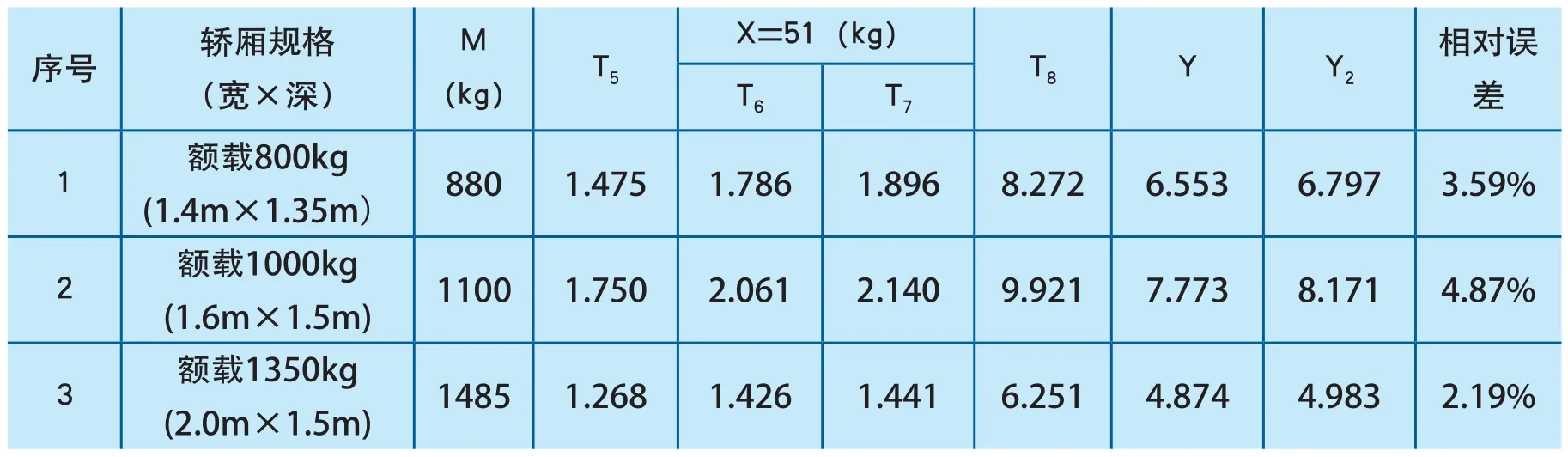
表3 （9）式计算值与现场检测数据对比

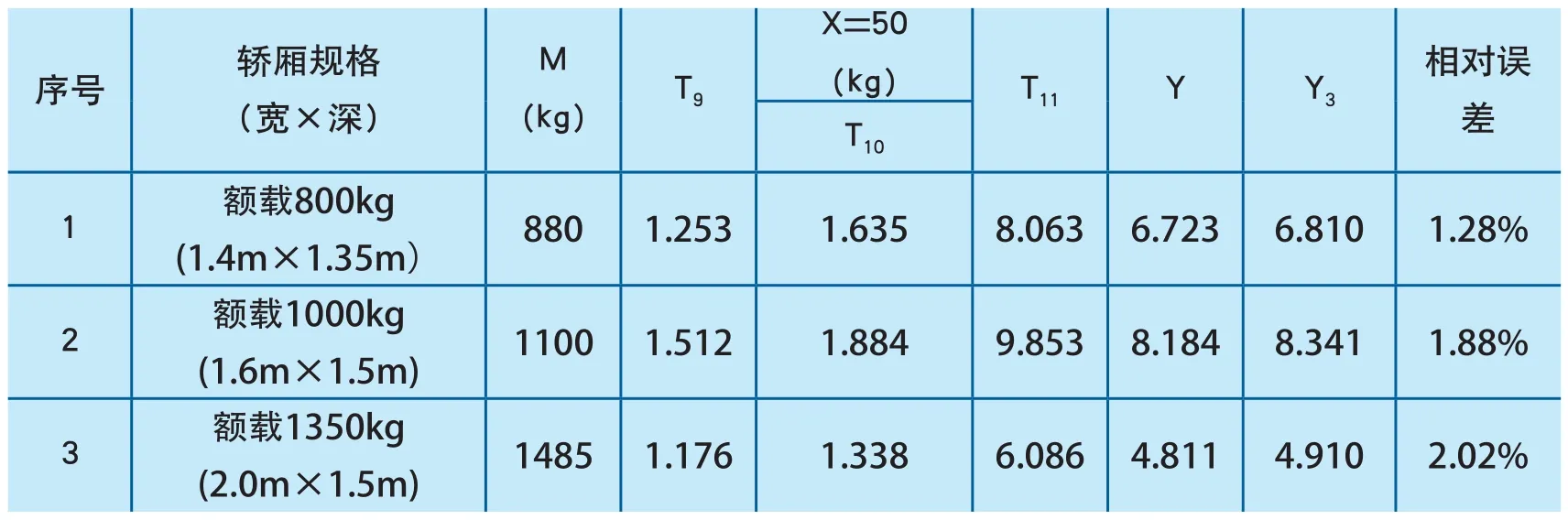
表4 （3）式计算值与现场检测数据对比

从表4可以看出，（3）式计算值Y与现场加载值Y3的相对误差较小，相符度较高。综合表2、3和4中数据可以看出，以（9）式或者（3）式对应的检测方法来判断超载保护装置的有效性是可行的。

分析了安装在电梯轿底的超载信号采集器的工作原理，通过有限元分析软件对轿厢数学模型进行了加载分析，提出了以小载荷时轿底中心与下横梁之间的距离变化量推算大载荷时的距离变化量，进而检测超载保护功能是否有效的方法，并在模型及现场检测数据中得到了验证，为研制该类超载保护装置检测仪提供了理论依据，使检验时无需搬运相应超载载荷的砝码，大大降低了检测成本及劳动强度，检测效率也大幅提高。

（作者单位：浙江省嘉兴市特种设备检验检测院）