开阔视野，呈现新知

万霞

[摘 要] 对新知教学的有效方式进行探索，是初中数学教学所应重点关注的课题. 创新新知教学方式的关键在于教学视野的开拓. 从教学设计的角度来讲，这主要是对教师们提出的要求. 为了实现富有实效而又灵活创新的新知教学，教师们需要解放固有的教学思维，不断开拓教学视野，考虑多方影响因素，打造多维度的数学教学过程.

[关键词] 初中数学；新知教学；创新方式

数学学习是一个不断遇见新知、理解新知并深化新知的过程，对新知识的接受和处理效果，直接关系到整个学习效果的理想与否. 初中是数学知识学习的基础阶段，这个时期知识内容的学习质量更关乎日后数学能力建立发展的状态. 因此，对于新知教学的有效方式进行探索，是初中数学教学所应重点关注的课题. 通过对当前新知教学现状进行调研，笔者发现，教学动作虽然井然有序，却也略显固化，尤其是在一些难度较大内容的教学过程中，很难将学生的思维热情调动起来，使教学效率有待提升. 由此，这种教学方式的创新显得十分必要.

运用“交流互动型”教学法，激

活学习热情

无论当前的教学内容是什么，来自学生心底的学习热情始终是推动学习活动高效进行的根本动力. 因此，在每一次新知教学开始之初，激活学生的学习热情都是活动开展的第一步. 从心理特点上来讲，初中阶段的学生喜好生动热闹的教学氛围. 如果能够将课堂教学气氛向这一方向打造，必将让学生在心理动力之下完成优质学习.

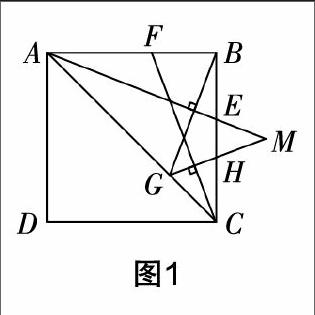
例如，在对平面几何的内容进行综合讲解时，笔者向学生提出了这样一个问题：如图1，四边形ABCD是正方形，点E和点F分别在边BC和AB上，BE和BF等长. 过点B作AE的垂线，与AC交于点G，再过点G作CF的垂线，与BC交于点H，点M是AE的延长线与GH延长线的交点. （1）求证：∠BFC=∠BEA；（2）求证：MA=BG+MG. 这道题虽然比较综合，涉及正方形、全等三角形等多个平面几何知识，但是，笔者并没有直接给学生揭晓答案，而是请大家自由讨论，寻找解答方法. 第一问的解答并不困难，到了第二问，学生们的讨论愈发热烈起来了. 在大家的思维碰撞和笔者的适时提示之下，学生们成功地找到了连接DG构造辅助线的方法. 这个交流互动的过程当中，大家不仅体会到了辅助线构造的解题方式，更表示应当将之进行条理化的总结，帮助日后综合性问题的解答.

“交流互动型”教学法的核心在于为学生提供了一个广阔的自由思考空间. 虽然教师主导能够更好地保证教学方向没有偏离，但是，也很容易让整个课堂气氛陷入凝固、死板的境地. 教师们应当认识到，交流互动并不是课堂教学的全部，而是在教师的适时引导中穿插进行的. 教师引导的存在，使得交流互动不会偏离主题；而交流互动的存在，也使得课堂教学不致枯燥乏味.

运用“探究参与型”教学法，有

效灵活思维

初中数学知识内容并不是浮于表面的，而是具有很多拓展深入的可能性. 只有意识到这些可能性，并将它们抓住，才能将数学教学的效能发挥到最大. 为了将数学知识的内涵全部发掘出来，需要从基础知识表面入手，开展灵活深入的探究，以全面的视角观察数学，从而收获最为有效的数学学习.

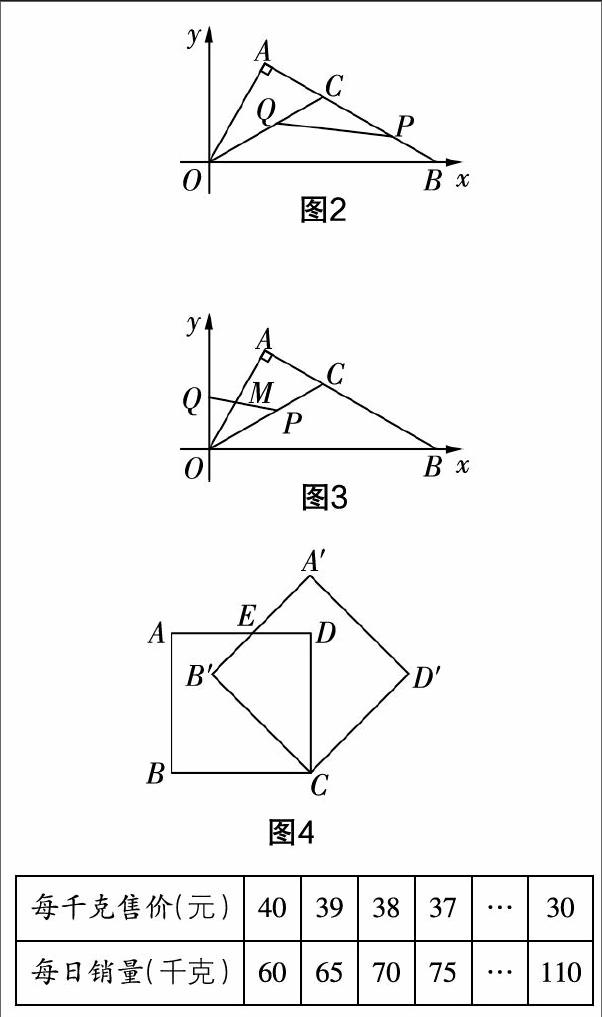
例如，在对函数与几何内容进行教学时，笔者发现，在深入探究的过程当中，二者存在着相交之处. 为了尽可能地延伸学生的思维路径，笔者特意设计了这样一道习题：如图2，Rt△AOB位于一个平面直角坐标系当中，其中点A是第一象限内的点，∠A是直角，∠AOB=60°，OB=2，且在x轴的正半轴上，OC是∠AOB的平分线，与AB交于点C. 现有一动点P，按照B—C—O的方向以每秒1个单位长度的速度运动，共运动t s. 与此同时，另一个动点Q按照C—O—y的方向以每秒1个单位长度的速度运动，并在点P运动到点O时同时结束运动. （1）OC和BC的长分别是多少？（2）若记△CPQ的面积是S，则S与t之间存在怎样的函数关系？（3）如图3，当两个动点运动时，PQ与OA相交于点M，那么，若要使△POM是等腰三角形，t应当取何值？这样一系列问题，学生在两种知识的结合之中体验到了一次综合完整的知识探究，并很好地将代数与几何知识结合了起来.

从探究活动的灵活性与自发性等特点来看，学生应当成为数学知识探究的主体. 只有当学生真正参与进来之后，他们才能感知到数学知识的灵动发展，并在发现新知的同时开拓思维. 这种思维层面上的优化，对于数学学习的长远发展都具有重要意义.

运用“媒体辅助型”教学法，深

入剖析知识

随着时代的不断发展，初中数学教学也在经历着方式方法上的持续变革. 与以往的单纯讲述相比，多媒体的介入使得课堂教学焕发出了全新的活力. 一方面，新鲜的教学形式为学生点燃了高涨的学习热情. 另一方面，很多复杂晦涩的知识内容在多媒体全面、灵活的展现之下变得细致、清晰了许多，这对于数学知识的剖析来讲，意义重大.

例如，在对正方形内容进行教学时，为了能够让学生将正方形的性质特点体会到位，笔者向大家提出了这样一个问题：现有一个正方形ABCD，若将其中的点C固定，并绕着点C将这个正方形进行旋转，成为正方形A′B′CD′，其中A′B′与AD交于点E，∠B′CB=30°，那么，AE的长度是多少？仅从文字表面上来看，刚刚接触正方形知识不久的学生很难发现其中隐藏的规律. 于是，笔者打开电脑中的“几何画板”软件，依照已知条件中的叙述将图形画出来，并运用其中的动画功能将正方形旋转的过程进行清晰演示（如图4）. 操作虽然简单，但在这样的反复演示之下，学生得以明确观察到其中哪些量变化了，哪些量没有变，进而发现正方形性质的存在，实现了知识内容的准确理解.

根据不同类型多媒体的呈现特点，其所适用的教学内容也存在一定的差异. 如果教学目的在于激发学生的思考兴趣，教师往往可以选择具有声、光表现能力的多媒体形式. 而如果教学目的在于阐明知识内容本身，教师便可以选择具有图形或动画表现能力的多媒体，化抽象为具体. 无论怎样，多媒体的介入辅助，都为初中数学知识的深入剖析注入了一剂强劲动力.

运用“学以致用型”教学法，理

论联系实际

在初中数学知识的学习过程当中，仅有理论层面的探究是远远不够的. 只有成功地将理论知识与实际应用联系起来，做到以数学理论解决实践问题，才能被评价为将数学知识学懂了. 这种学以致用的思维路径应当普遍存在于整个数学知识学习过程当中. 因此，以之作为新知教学的重要方法，帮助学生在初中阶段建立起这种有效的思维习惯，对于数学学习来讲非常重要.

例如，在对函数内容进行教学时，笔者大胆加入了如下思考题：某水果店想要开始销售太阳果，并通过市场调查得出了下表中的销售规律. 若太阳果的进价是20元/千克，为了获得最大利润，应当将其单价由40元/千克下调到多少元？实际问题的出现，立刻拓宽了学生的思维视野，在解题的同时，大家对于函数的认知也更加灵活、深刻了.

不难发现，以学以致用的方式呈现数学新知的操作过程并不复杂. 实际上，在初中数学的各类测试当中经常出现的应用性问题，就是这一教学思想的集中体现. 如果在新知呈现阶段便引导学生主动将之联系到实际生活当中，便可以在教学开始之初触发大家学以致用的思维方向，为深入、有效理解知识埋下伏笔.

创新新知教学方式的关键在于教学视野的开拓. 从教学设计的角度来讲，这主要是对教师们提出的要求. 为了实现富有实效而又灵活创新的新知教学，教师需要解放固有的教学思维，不断开拓教学视野，考虑多方影响因素，打造多维度的数学教学过程. 在这样的创新教学体系下，学生得以感受到焕然一新的学习氛围，并在全新的教学模式之下感受到初中数学的新面貌.