感应分流器的误差特性研究及其试验*
2017-01-10熊魁姜春阳雷民殷小东解岩刘浩
熊魁,姜春阳,雷民,殷小东,解岩,刘浩
(1.中国电力科学研究院,武汉430074;2.国网天津市电力公司,天津300000)
0 引 言
作为一种电流比例标准,感应分流器可以获得很高的准确度和稳定性,在上世纪七十年代就有人对其进行了研究[1-2]。但是随着双级电流互感器和电流比较仪在电参量测量领域的广泛应用,感应分流器逐渐淡出了研究者的视线以及电流计量领域。实际上,通过良好设计而制造的感应分流器,既可以达到很高准确度,又具有一定的带负载能力,因此能减少校验过程的复杂程度而方便应用于电流比例的测量,可以运用于常见的标准二次电流为5 A、1 A以及二次为毫安级小电流的工频电流比例标准的量程扩展,并且能结合电流比较仪组成电流自校系统进行电流比例量值溯源[3-7]。
目前对于感应分流器的研究还为数不多,文献[2]主要侧重于感应分流器的校验方法研究,文献[3-4]关注了感应分流器的量程扩展方法及其应用。现有文献没有对感应分流器的误差原理和误差特性进行研究,而这对指导感应分流器设计和误差校验,并提高其准确度等级是十分必要的。本文主要对感应分流器的结构和基本原理进行了研究,推导单级和双级感应分流器的T型等效电路模型和误差表达式,阐述了其误差性能,从理论上得出了影响两类感应分流器误差性能的参量和条件,在此基础上设计感应分流器并进行试验验证,最终给出感应分流器的基本计量特性和相应结论。
1 感应分流器结构和电路图
单盘感应分流器的基本结构是自耦式电流互感器,一般做成十段式或者十二段式,在铁心上绕制多段均匀且匝数相等的绕组就可以构成一个简单的单级感应分流器,原理图如图1所示[5]。而单盘感应分流器可以做成单级结构,也可以做成多级结构,常用的双级式单盘感应分流器的原理如图2所示,主要由主铁心T1、辅助铁心T2、比例绕组W2、补偿绕组WB构成,R和r分别为比例绕组和补偿绕组的引线电阻加接触电阻。其中,主铁心上均匀绕制补偿绕组,然后在辅助铁心外绕制比例绕组,比例绕组根据需要分段绕制,若是分十段绕制的,包括头尾共有十一个抽头,补偿绕组的匝数与十段比例绕组匝数总和相等。辅助铁心也可以设计成屏蔽结构铁心,同时起到屏蔽杂散磁场的作用。
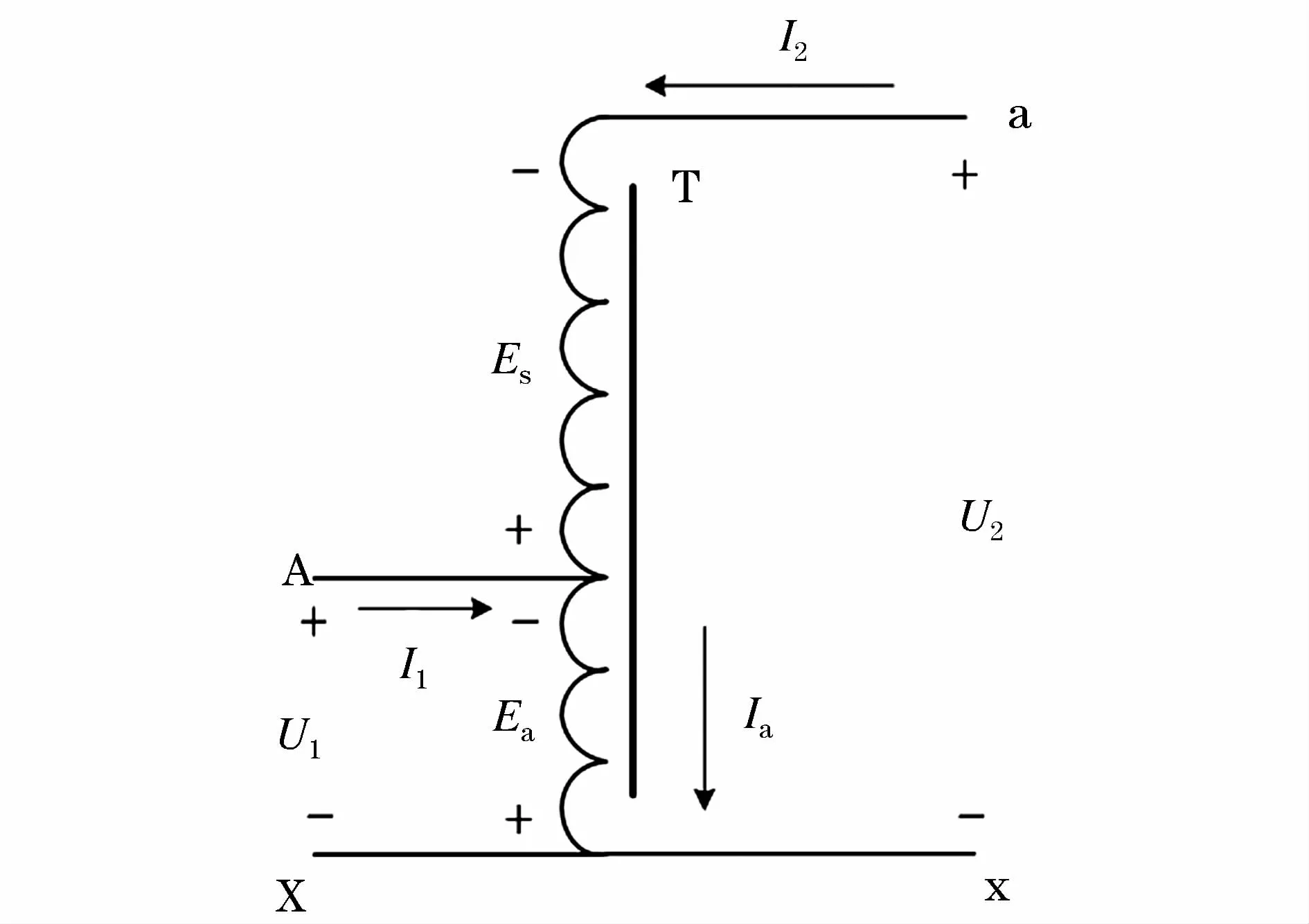
图1 单级感应分流器Fig.1 One-stage inductive current divider
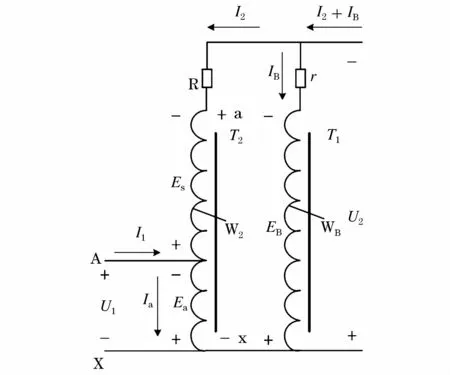
图2 双级级感应分流器Fig.2 Two-stage inductive current divider
由于感应分流器共用部分一次和二次绕组而没有物理隔离,使得一次电流压降反向补偿了二次电流压降,显著的减小了二次回路的等效内阻,导致感应的励磁电势很小,铁芯处于弱励磁状态,而双级结构的引入进一步弱化了主铁芯结构的励磁电势,并提高了感应分流器的带载能力,使其能达到较高的准确度等级[6-10]。
2 单级感应分流器的T型等效电路模型
为了研究感应分流器结构和参数对其误差性能的影响,需要推导其等效电路模型,根据等效电路分析各个参量之间的关系。首先分析单级感应分流器的T型等效电路模型,如图1所示取电流、电压正方向,设其一次绕组和二次绕组匝数分别为N1、N2,则额定变比为K=N2/N1。工作时,由磁势平衡方程和回路电压方程,可以得出相应的推导公式。
根据磁势平衡方程式有:

式中I0为感应分流器的励磁电流。上式代入变比K,得:
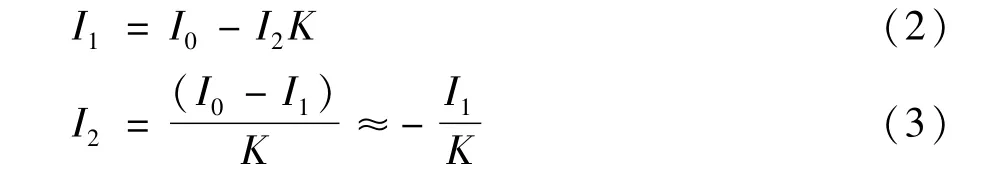
对一次绕组A—X的电压方程为:

式中Za为一次绕组A—X的阻抗;Ia为一次绕组A—X中的电流;Ea为主磁通在一次绕组A—X中的感应电势。
而有:

式中E2为主磁通在二次绕组a—x中的感应电势;Zm为励磁阻抗。
Ia的数值为I1和I2的代数和:

将式(3)、式(5)、式(6)代入式(4)可以得到:
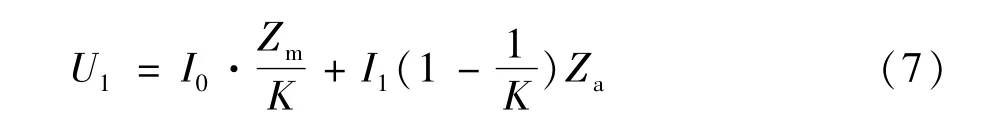
绕组a—A的电压方程为:

式中Zs为绕组a—A的阻抗;Es为主磁通在绕组a—A中的感应电势。而:
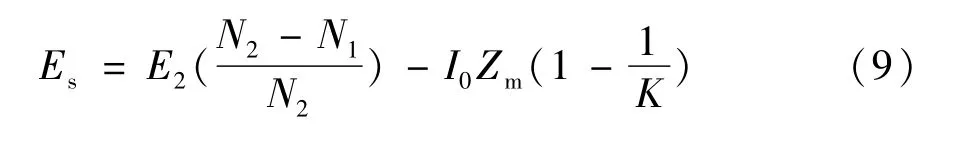
代入式(8)得:
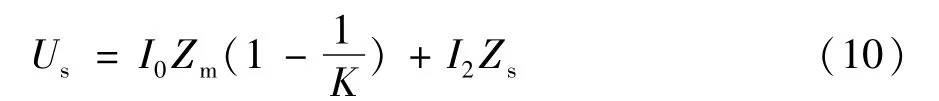
因此,可以推出二次电压方程为:
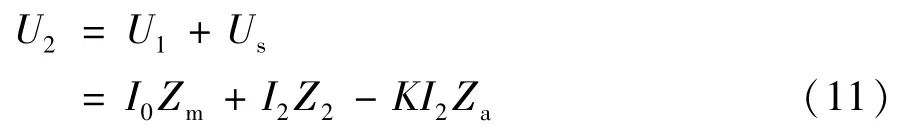
通过U′2=U2/K,I2=I′2/K折算到一次侧,代入式(11)则有:
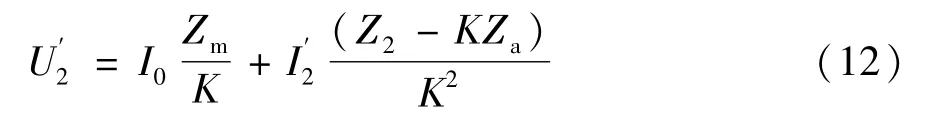
由式(7)、式(12)可以得出单级感应分流器的T型等效电路如图3所示,为二次负荷,与电流互感器类似,折算后的一次电流与二次电流的值近似相等,相位相差180°,励磁电流造成了感应分流器的主要误差。
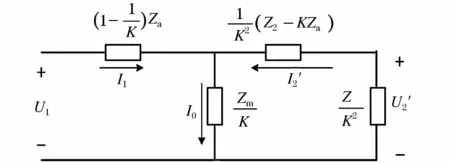
图3 单级感应分流器的T型等效电路图Fig.3 T-network equivalent circuit diagram of one-stage inductive current divider
根据复数误差的定义,折算到输出端的误差为:
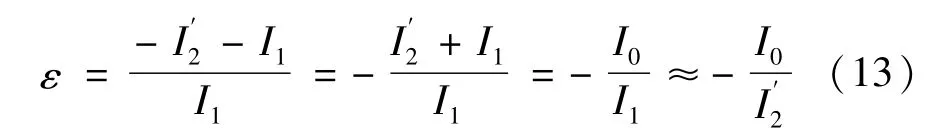
据等效电路有:
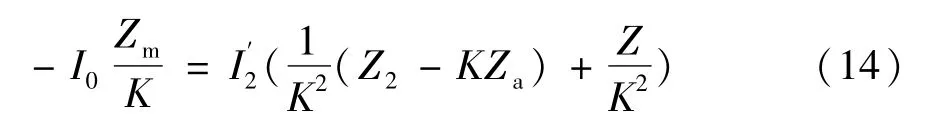
所以结构简单的单级感应分流器误差为:
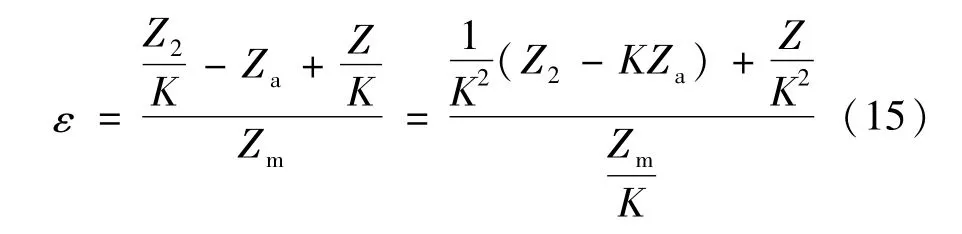
上述误差即所谓各段绕组内阻抗不均匀和二次负荷引起的误差。由此可以看出单级感应分流器励磁误差要小于同条件下的电流互感器误差,其误差主要来源于三参量:
(1)励磁阻抗 Zm的大小,由于 Zm≫Z2(Z),励磁阻抗Zm对误差影响很大。要求尽量选用磁导率高的铁心;
(2)整个比例绕组内阻抗的均匀性,若各段比例绕组内阻和漏抗相等,则ΔZ=Z2-KZa=0,误差表达式(15)分子的第一部分为零;
(3)二次负荷的大小,二次负荷越小感应分流器误差越小,理想状态下Z=0,误差表达式(15)分子的第二部分为零。但实际工作时必然会接入一定的二次负荷,因此限制了单级感应分流器的应用和准确度等级的提升。
3 双级感应分流器的T型等效电路模型
相对于单级结构,由于补偿绕组和辅助铁心的引入,双极结构感应分流器拥有更小的误差,并具备较强的带载能力。同理,由电势和磁势平衡原理可推出双级感应分流器的T型等效电路模型,如图2所示取电流、电压正方向,设其一次绕组和二次绕组匝数分别为N1、N2,补偿绕组匝数为NB,则额定变比为K=N2/N1。
根据磁势平衡方程式有
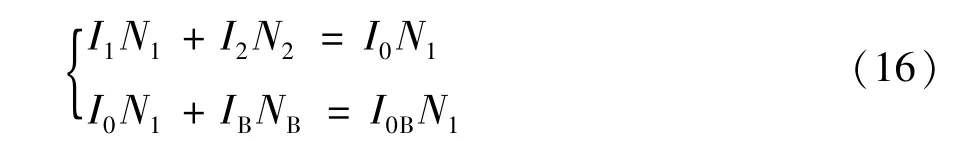
式中I0为感应分流器的辅助铁心结构的励磁电流;I0B为感应分流器的主铁心结构的励磁电流。上式代入变比K,且I0和I0B忽略不计,可得:

且有:

式中E2为磁通在二次绕组a—x中的感应电势;Zm2为辅助铁心结构的励磁阻抗。
联立式(17)、式(4)、式(18)、式(6)、式(8)、式(9)、式(10),可以推出二次电压方程为:
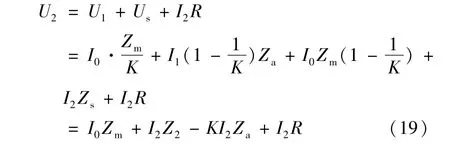
则有:
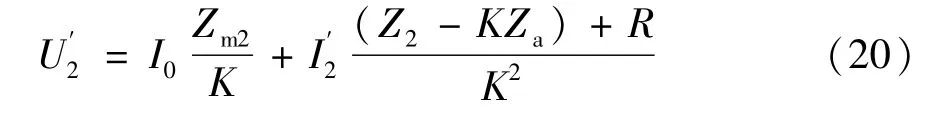
对补偿绕组WB的电压方程为:
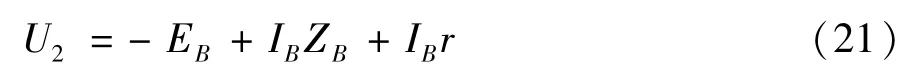
而:

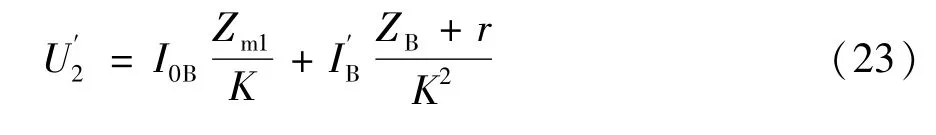
通过简化,由式(20)、式(23)可以得出双级感应分流器初始的T型等效电路如图4所示。根据电路的三角形和星形等效变换,且由于各绕组阻抗远远小于相应励磁阻抗,则原图4所示T型等效电路可以转化为标准的T型等效电路,如图5所示,Z为二次公共负荷。
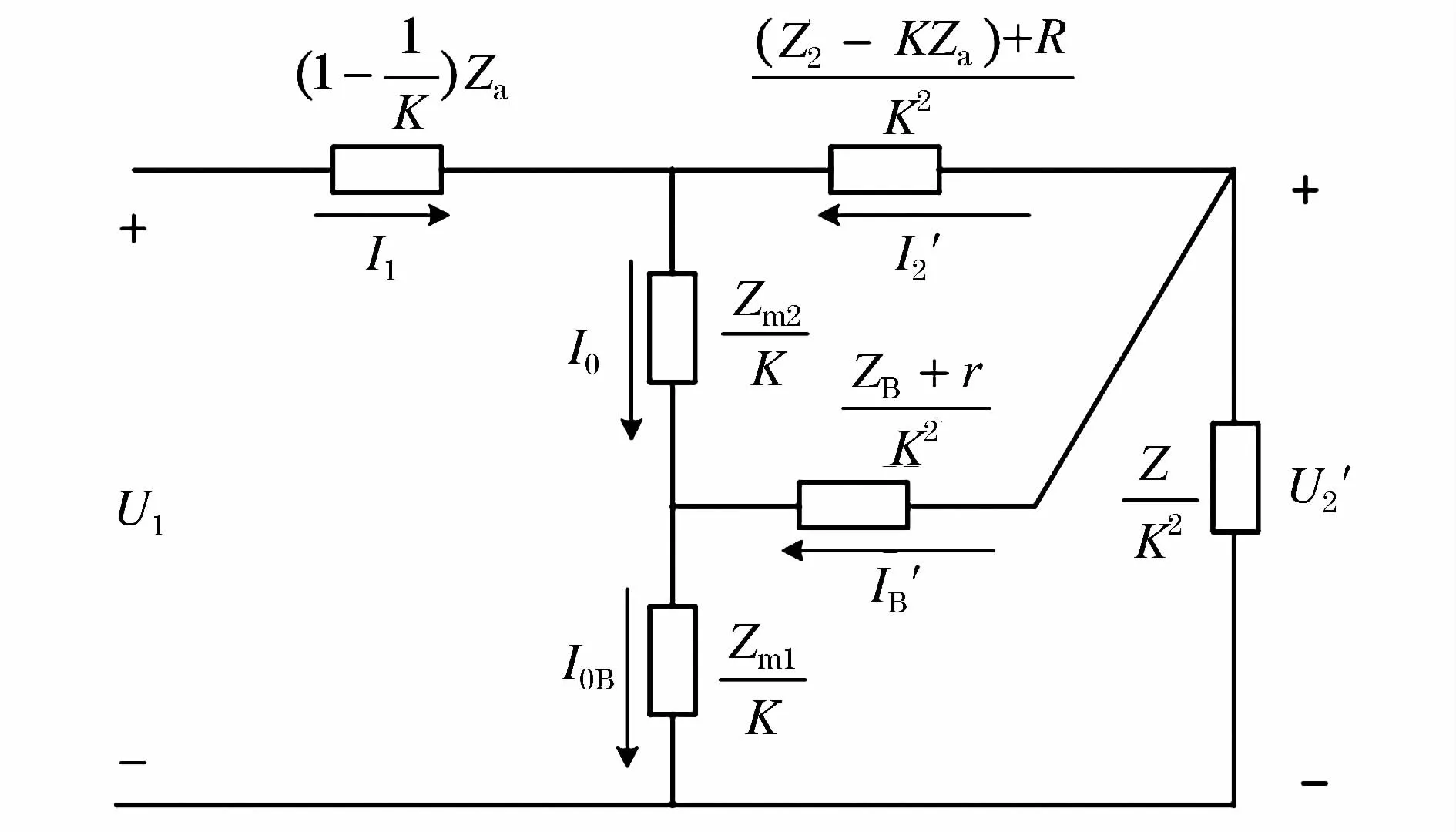
图4 双级感应分流器初始的T型等效电路图Fig.4 Original T-network equivalent circuit diagram of two-stage inductive current divider
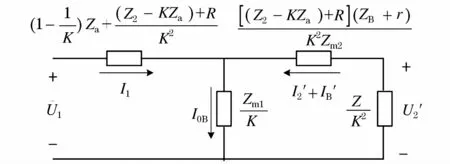
图5 双级感应分流器的标准T型等效电路Fig.5 Standard T-network equivalent circuit of two-stage inductive current divider
同理,可以得双级感应分流器误差为:
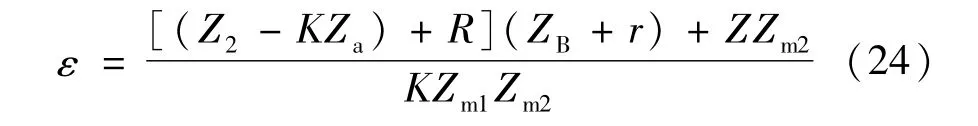
相对于单级感应分流器,双级感应分流器有若干相似性质,而上式与式(15)的区别主要在于分子部分增加了ZZm2,分母部分增加了Zm1,即:
(1)当双级公共负荷为零时,感应分流器误差为:
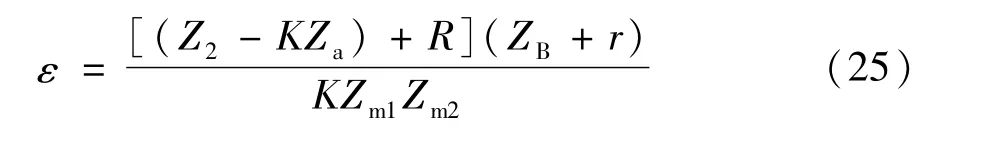
相当于在单级误差公式基础上乘以ZB/Zm1因式,且ZB<<Zm1,使双级结构可提高其准确度1~2个数量级,这点可与双级电流互感器类比,但是双级感应分流器理论上要比同条件下双级电流互感器准确度高,因为其二次等效内阻接近于零,主铁心磁密更低;
(2)当双级公共负荷增加时,感应分流器误差也相应增加,即为公式(24)。误差范围处于双级感应分流器和单级感应分流器之间,而公共负荷的继续增加会逐渐破坏双级结构的工作条件,使其误差特性恶化;
(3)当双级公共负荷增到使[(Z2-KZa)+R]·(ZB+r)<<ZZm2时,公式可化简为:

相当于单级感应分流器带二次负荷的误差,则双级结构没有起作用。
4 检定线路和误差试验
电流比较仪检定双级感应分流器线路如图6所示。图中Ta为供电电流互感器,变比为N/1,由它给校验仪工作回路供电,Tx为被检感应分流器,一次电流抽头依次为0~N,T0为标准电流比较仪,变比与被检一致。由于感应分流器是自耦式的,其一次和二次绕组没有隔离,当一次回路通过感应分流器或者电流比较仪的一次补偿绕组间接接地时,二次回路也处于间距接地,因此试验线路中的二次回路不能再接地,包括校验仪的工作回路也不能接地,需要将D端子与接地端子的连接去除,使D端子不接地。
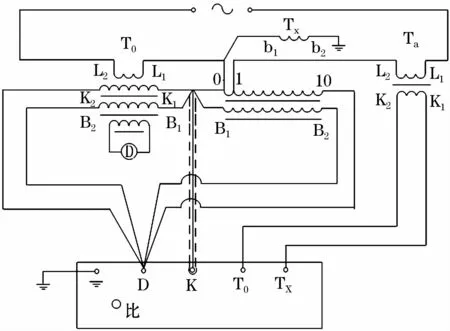
图6 电流比较仪检定双级感应分流器线路Fig.6 Calibration circuitwith current comparator and inductive current divider
进行本试验的感应分流器变比为5 A~50 A/5 A,比例绕组由10段串接而成,使用不同的抽头可以得到N/10的电流比,足以覆盖1、2、5的电流比。电流比较仪按相同的电流比配合感应分流器进行检定,供电互感器为0.2级的同变比电流互感器,通过如图6所示试验线路对双级感应分流器50/5、25/5和10/5三个变比进行检定,检定结果见表1。表中f为比值差,δ为相位差,其中比值差绝对值小而跨度大,相位差相反绝对值大而跨度小,因此可以对被检的感应分流器通过传统方法进行补偿,主要是对相位差进行补偿,补偿后的结果见表2。
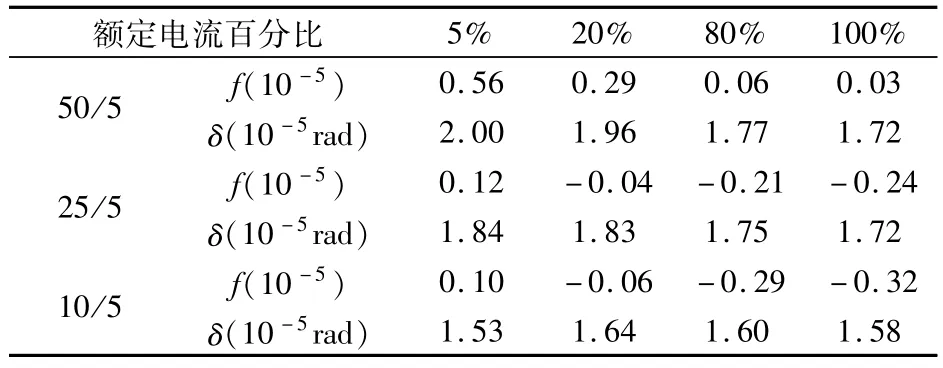
表1 双级感应分流器误差Tab.1 Error of two-stage inductive current divider
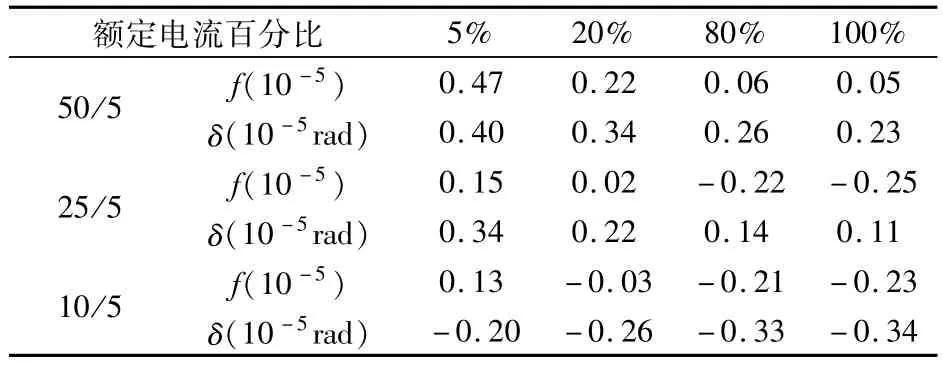
表2 补偿后的双级感应分流器误差Tab.2 Error of two-stage inductive current divider after compensation
通过表2可以看出,补偿后双级感应分流器比值差小于5×10-6,相位差小于4×10-6rad,在额定电流20%以上时,误差变化相当平坦,因此具有较大应用潜力。
5 结束语
基于感应分流器的结构和电路原理,推导了单级和双级感应分流器基本误差公式,同时得到了相应的T型等效电路模型,并进行了误差校验,可到如下结论:
(1)单级感应分流器误差主要取决于励磁阻抗的大小,各段比例绕组内阻抗的均匀性,二次负荷的大小,设计良好的单级感应分流器准确度等级高且使用方便;
(2)双级感应分流器误差特性除了和单级结构类似的部分外,其误差主要受二次公共负荷的影响,为了提高其准确度等级,需要通过优化接线等措施尽量减少公共负荷,从而减小励磁电势,使得主铁心趋近于零磁通状态;
(3)通过电流比较仪检定双级感应分流器的的线路,进行误差试验,试验结果表明,双级感应分流器比值差不超过5×10-6相位差不超过4×10-6rad。
