计及保护约束的分布式电源优化配置

陈星欣，吕飞鹏，白懿鹏

（四川大学电气信息学院，成都610065）

0 引 言

近年来，智能电网的建设成为国内外关注的热点问题，而智能电网所包括的特点有研究和发展绿色能源、提高电网运行可靠性、创造更好的兼容性等。以太阳能光伏发电、风能发电、小型水电为主的分布式电源（Distributed Generation，DG）符合当今环境保护、节能减排和可持续发展的要求。随着DG技术发展的成熟，DG在配电网中所占比重越来越大，多个DG同时并网的现象也会越来越普遍［1-3］。但是，DG接入配电网位置和容量的不同，会对配电网的潮流产生不同的影响，进而对配电网继电保护系统的运行产生影响。所以DG的选址和定容是DG配置过程中需要重点考虑的问题，并且当在对DG的接入进行优化的时候，继电保护应作为一个重要约束条件考虑在其中。

许多学者针对DG配置问题从不同方向进行了一系列的深入研究，并且取得了相应的研究成果。文献［4］以有功网损最小为目标函数，利用免疫遗传算法对分布式电源的选址了定容进行了优化，但是在约束条件中并没有考虑DG接入对继电保护保护的影响。文献［5］在考虑继电保护的基础上，用传统遗传算法对DG可接入配电网的最大容量进行了计算，却并没有考虑到电网的经济性。文献［6］是将对继电保护的考虑转化为区域内接入DG总容量最小来计算配电网的经济性，所以并没有真正做到对短路电流进行约束。文献［7］虽然有以短路电流为约束条件来进行优化配置，但文章使用的是最传统的遗传算法，计算速度不够快，收敛性不够好，有待改进。

本文在上述研究成果的基础上，重点考虑了DG选址和定容对配电网继电保护系统运行的影响。在以传统配电网三段式电流保护为依据的前提下，建立了以有功网损为最小的目标函数。在利用牛顿-拉夫逊法计算配电网潮流的基础上，使用自适应遗传算法对目标函数进行寻优。最后，通过算例验证了本文所提模型和算法的有效性。并将结果同不考虑短路约束的优化结果和使用传统遗传算法得出的结果分别进行比较，以此证明考虑继电保护条件的必要性以及改进算法的优良性。

1 DG接入对继电保护的影响

配电网一般配置三段式电流保护。DG接入配电网后，系统由单电源供电变为多电源供电，当线路发生短路时，短路电流的大小和方向会因此改变。

图1为典型的简单放射状配电网系统，P1、P2、P3、P4分别为相应馈线的保护装置，DG从节点C接入配电网。

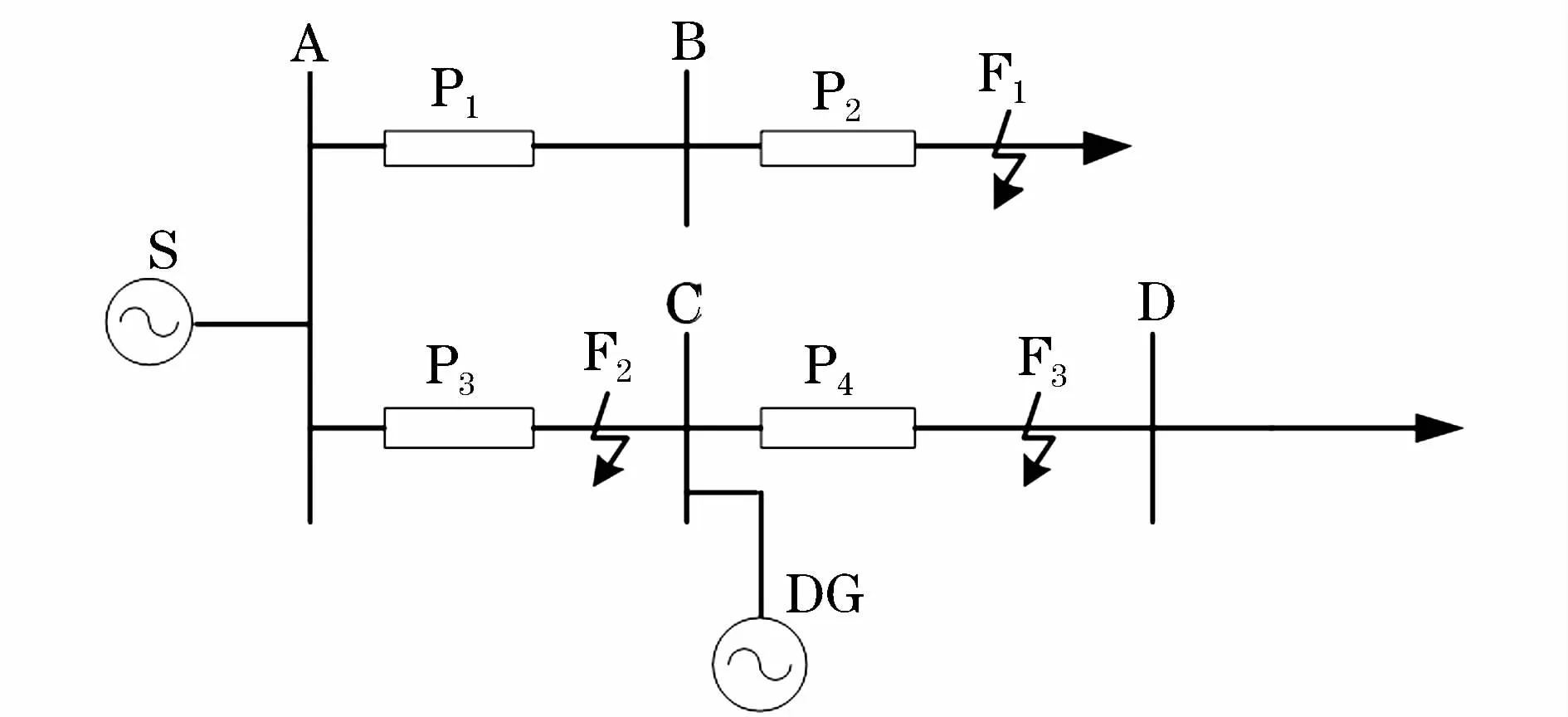
图1 DG接入的简单配电网系统图Fig.1 Distribution network system diagram of FIG with DG

1.1 DG接入的相邻馈线发生短路

当相邻馈线末端发生短路故障F1时，系统S和DG向保护1和2提供叠加的短路电流，与DG接入前相比，短路电流增大，其值可能大于P1原有的I段整定值，使得P1误动，造成P1和P2失去配合。同时，P3也会流过DG提供的反向电流，当DG容量较大时，反向电流的值可能大于P3原有的I段整定值，造成P3误动。

1.2 DG接入的上游发生短路

当DG上游馈线AC发生短路F2时，保护装置均能正常动作，但是当P3动作后，DG下游会形成孤岛运行，同时，DG会一直向故障点提供短路电流，这将影响系统的可靠性。

1.3 DG接入的下游发生短路

当DG下游馈线CD发生短路F3时，保护P1、P2能正常动作。流过保护3的短路电流虽然只由系统S提供，但是因为DG的接入，故障电流会比接入前小，这可能会造成P3后备保护的拒动。而流过保护4的短路电流由系统S和DG共同提供，短路电流的增大可能会使得P4的保护距离增加，从而失去选择性。

当系统中含有多个DG时，分析方法类似。由上述分析可知，DG的接入会对配电网的继电保护和系统的可靠性带来不利的影响，所以在优化配置分布式电源时，考虑继电保护的约束必不可少。在传统三段式电流保护中，I段瞬时电流速断保护最为重要，所以本文重点分析的是配电网中接入DG后，对保护装置原有电流保护的I段的影响。采取的思路是对短路电流进行约束，用惩罚函数淘汰掉短路电流大于保护装置原有I段整定值的解。具体过程将在下文中加以说明。

2 分布式电源选址定容的数学模型

2.1 目标函数

建立以配电网有功网损最小为目标的数学模型［8］：

式中L为电网总支路数；Rij为支路ij上的支路电阻，Iij为支路电流。

2.2 约束条件

约束条件分为不等式约束和等式约束［9-11］。

2.2.1 潮流等式约束条件：

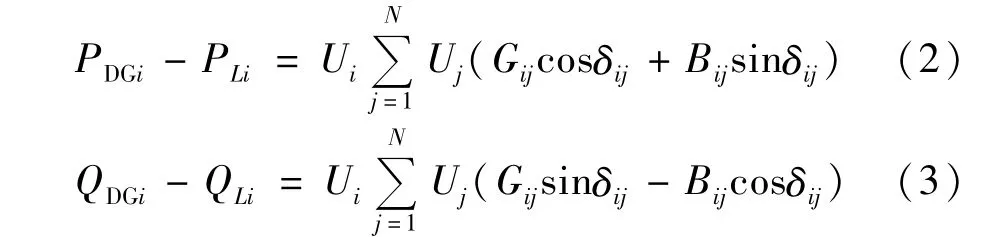
式中Ui为节点i的电压幅值；Uj为节点j电压幅值；Gij为节点i和节点j之间的支路电导；Bij为节点i与节点j之间的支路电纳；δij为节点i与节点j之间的电压相位差。

2.2.2 节点电压上下限约束条件：

式中Uimin、Uimax分别为节点i电压上、下限。

2.2.3 电流约束：

式中Iijmax为支路ij上允许通过的电流上限。

2.2.4 短路电流约束：

式中ICBi为流过保护装置i的短路电流；IIop.CBi为保护装置i的I段整定值。

2.2.5 分布式电源最大安装总容量约束：

式中N为分布式电源个数；PDGi为节点i接入DG的安装容量；PLi为节点i上的负荷。

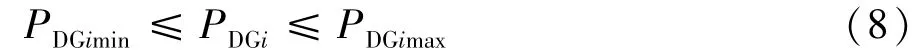
式中PDGimin、PDGimax分别为节点i允许接入容量的上、下限。

2.3 约束条件的处理

对不等式约束条件的处理，很多文献采用惩罚函数的形式体现在目标函数中［12-13］。本文将式（4）到式（6）的约束条件以该形式加入目标函数，而式（7）和式（8）则作为约束条件用于自适应遗传算法中对初始种群的筛选。

2.3.1 节点电压惩罚函数：

式中K（Ui）为节点i压越限的惩罚函数；kiU为节点i电压越限的惩罚因子，kiU=1 000。

2.3.2 支路电流惩罚函数：

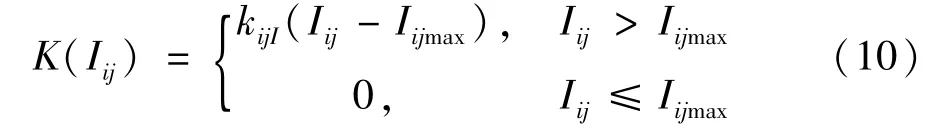
式中K（Iij）为支路ij电流越限的惩罚函数；kijI为支路ij电流越限的惩罚因子，kijI=1 000。

2.3.3 短路电流惩罚函数：

杨建斌利用有限元法分析了沥青路面加宽时差异沉降引起的附加应力，通过调整路面参数探讨了路基加宽的设计方法[3]。余常俊提出为了增加新老路面的连续性，需要在基层、下面层和中面层设置台阶，并就拼接台阶的施工工艺做了具体介绍[4]。曾庆春等结合佛开高速公路改扩建工程，利用有限元法计算了加宽时新老路基差异沉降对路面结构层的附加应力，新老路基差异沉降对路面结构层产生的过大附加应力会使路面发生破坏[5]。

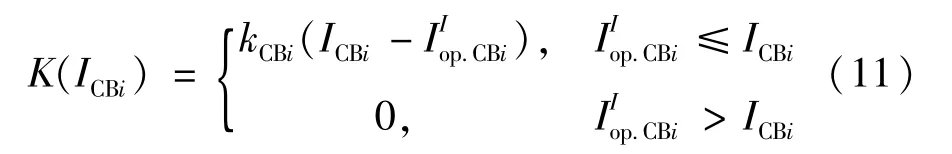
式中K（ICBi）为流过保护装置i的短路电流越限的惩罚函数；kCBi为该短路电流越限的惩罚因子，kCBi=1 000。

将三个惩罚函数与网损公式相加得到新的目标函数。计算过程中遇到不满足约束条件的情况时，目标函数的值会很大，在优化过程中这样的值会被剔除，进而留下最优解。

新的目标函数如下：

式中N为节点总数；n为支路数。

3 基于自适应遗传算法的分布式电源选址定容规划

3.1 自适应遗传算法

遗传算法是一种优化算法，是从代表问题可能潜在解集的一个种群开始的，中间按照适者生存、优胜劣汰的原理，逐代演化产生出越来越好的解。原始的遗传算法自身不够完善，求解时容易陷入局部最优，并且稳定性不够。本文将采用自适应遗传算法，根据适应度函数自身的特点对交叉率和变异率进行改进，使其随着适应度值自动改变。

3.1.1 编码方式

二进制编码是遗传算法最常采用的编码方式，但是因为求解时涉及到分布式电源的选址定容问题，二进制编码过于复杂且低效，所以本文选择浮点数编码。

假设一组变量 X={X1，X2，X3…Xn}，Xi表示节点i处接入分布式电源，Xi为零即表示节点i不接入分布式电源［14］。

3.1.2 产生分布式电源位置和容量的初始种群

对于分布式电源选址和定容的初值，如果完全随机产生初始种群，就很可能出现很多不可行解，这样会导致计算出错或者收敛速度慢等问题。所以在产生初始种群的这个过程中，将加入式（8）和式（9）的约束条件，使初始种群的选择范围缩小，这样有利于提高算法的计算速度和收敛性。

3.1.3 计算适应度值

遗传算法在进化搜索中基本不利用外部信息，仅以适应度函数为依据，利用种群中每个个体的适应度值来进行搜索。一般而言，适应度函数是由目标函数变化而来，本文直接将目标函数作为适应度函数，并设置为对应适应度值越小的个体越有利于留下来。

3.1.4 遗传操作

遗传操作的核心是选择、交叉和变异。遗传算法通过这三个步骤产生新一代种群来实现群体进化。各项参数中交叉概率Pc和变异概率Pm的选择是影响遗传算法行为和性能的关键所在，本文使用的自适应遗传算法就是对这两个概率进行改进。本文是求适应度值最小，所以对于适应度值低于种群平均适应度值的个体，给予较低的Pc和Pm，使得该解得到保护从而顺利进入下一代；而高于平均适应度值的个体，需要对应较高的Pc和Pm，使该解能被淘汰掉。同时，使群体中最小适应度值的个体的交叉率和变异率不为零，分别设为Pc2和Pm2，这就相应地提高了群体中表现优良的个体的交叉率和变异率。使得它们不会处于一种近似停滞不前的状态。

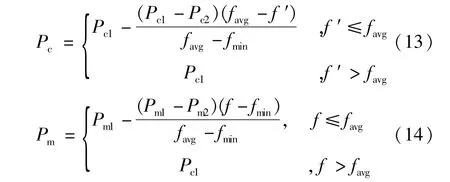
式中fmin为群体中最小的适应度值；favg为每代群体的平均适应度值；f′为要交叉的两个个体中较小的适应度值；f为要变异个体的适应度值；Pc1和Pm1为算法中最初设定的交叉率和变异率。其中，Pc1=0.9，Pc2=0.6，Pm1=0.1，Pc2=0.001

3.2 算法求解流程

自适应遗传算法的具体求解流程图如图2所示［15］。

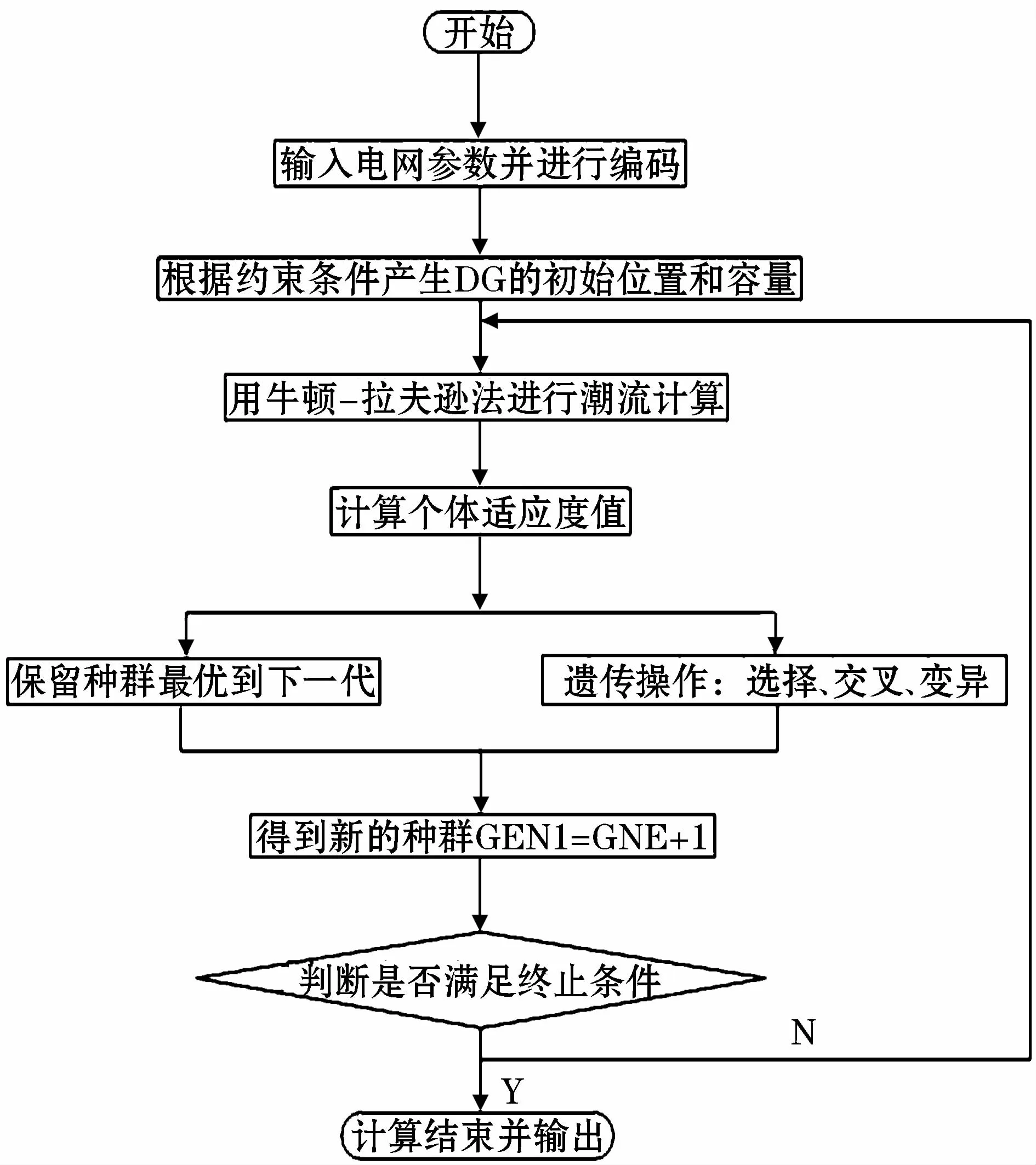
图2 自适应遗传算法的具体求解流程图Fig.2 Specific flow chart of the adaptive genetic algorithm

4 算例分析

本文的算例采用IEEE33节点配电网模型，但在一些数据上进行了适当的调整［16］，同时在原有模型上增加五个保护装置，用于监测短路电流，以确保在不改变装置原整定值的前提条件下，DG优化接入配电网后，配电网能正常运行。系统接线图如图3所示。

图3 IEEE33节点配电网系统图Fig.3 Distribution network system diagram of IEEE33 node

系统网络额定电压为10 kV，基准容量为100 MVA，节点8为平衡节点，节点0为电源点，电压为10.6 kV，系统总有功功率为8.714M W，总无功功率为5.861 Mvar。初始种群规模为50，最大迭代次数为100。

五个保护装置I段的整定值见表1。

表1 保护装置I段整定值（p.u.）Tab.1 First zone setting value of the protection device

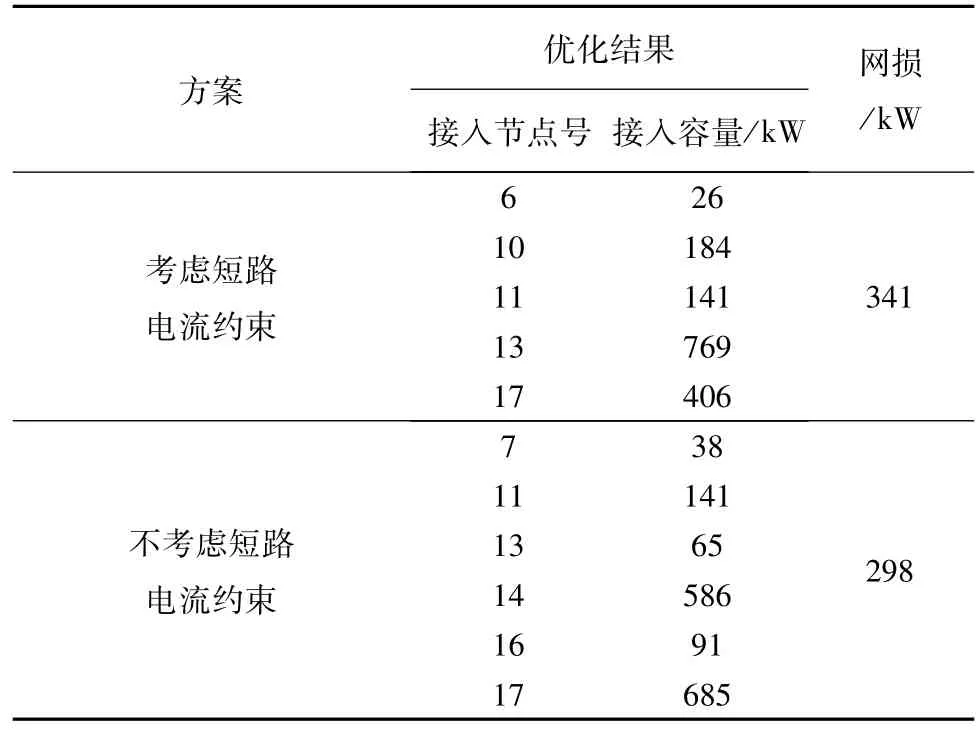
表2 两种方案的优化结果Tab.2 Optimization results of two kinds of schemes

从表2可以看出考虑短路电流约束后，分布式电源的配置方案与不考虑短路电流时是不同的。此时，虽然网损有所增加，但是由于考虑了短路电流的约束作用，配电网的继电保护系统不会发生误动作，保证了电网的可靠性。可见，在优化分布式电源的配置过程中，计及短路电流的约束是十必要的。

表3为自适应遗传算法与传统遗传算法计算结果比较。

表3 两种方法的计算结果Tab.3 Calculation results of twomethods

从表3可以看出，采用自适应遗传算法得出的结果与传统遗传算法的计算结果不仅非常接近而且还更优，这说明了将自适应遗传算法用于分布式电源的选址定容是可行的。图4为两种算法在优化过程中的收敛情况，由图可知，自适应遗传算法在收敛性和适应性上均优于传统遗传算法。

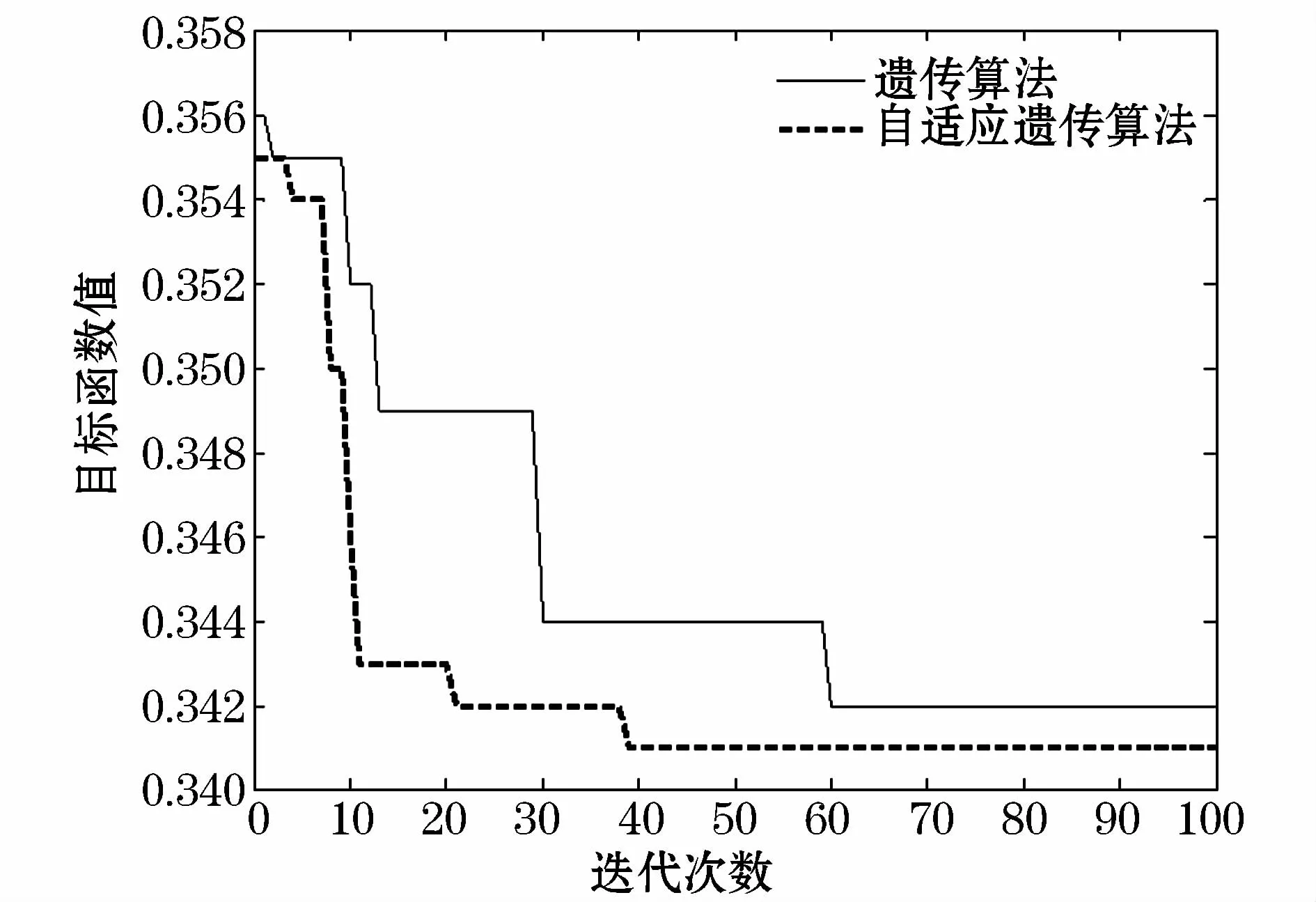
图4 自适应遗传算法和传统遗传算法收敛性对比图Fig.4 AGA and GA convergence comparison diagram

5 结束语

由集中式发电向分布式发电的转变是以后电网发展的趋势，所以对分布式电源入网的研究势在必行。本文在以有功网损最小为目标，重点考虑短路电流约束的基础上用自适应遗传算法来规划了DG接入配电网的位置和容量。仿真结果表明：（1）DG接入配电网后，网络的有功损耗明显减小，说明DG的接入对网络本身是有利的；（2）在对DG进行优化配置的过程中，计及继电保护的影响是必要的；（3）自适应遗传算法相比传统的遗传算法存在收敛性和适应性上的优势。