基于解耦双同步坐标变换的三相锁相环研究

唐轶，谢永强，王扬，刘全景，朱玉振

（中国矿业大学，江苏 徐州221008）

0 引 言

电网同步技术是电网中各功率变换器控制系统中的一个重要环节，它可以为其提供电网幅值、相位和频率等参数，以达到功率变换器与电网同步工作的目的。锁相环（PLL）作为一种优秀的同步技术，现已被广泛应用于静止无功发生器（D-STATCOM）、有源滤波器（APF）、并网逆变器等功率变换器当中。锁相环技术可以分为两类：开环锁相环与闭环锁相环。开环锁相环如过零检测，通过检测过零点时间来计算相位，因其对电压信号比较敏感，实际应用中，当电压幅值、相位以及频率发生突变时检测效果不佳。闭环锁相环研究较多的主要为三相同步锁相环（Synchronous Reference Frame Phase-Locked Loop，SRFPLL）。文献［1］叙述了SRF-PLL的基本原理，可以在三相电压平衡的情况下准确快速的锁定相位信息，但在三相不平衡情况下无法准确检测；文献［2］提供了一种延时T/4（T为工频周期）的方法，但是当频率发生波动时，无法准确分离正负序分量，检测误差很大；文献［3］提出了一种基于对称分量法延时T/3的方法，其缺点与延时T/4方法类似；文献［4］提出一种基于遗忘算法的锁相环技术，可以有效的分离正负序电压信号，检测各电网信号，但是当电网谐波含量较多时计算量较大，误差较高；文献［5］首先分析了引起锁相环误差的原因，提出了一种基于双同步坐标变换的锁相环，通过提取负序同步旋转坐标变换下的直流分量对正序同步旋转坐标变换下的q轴分量进行补偿，从而准确快速锁定基波电压正序相位。该方法可以在一定条件下实现电网各信号的准确检测，但忽视了正序同步旋转坐标系与负序同步旋转坐标系下各分量的耦合关系，故检测结果存在误差［6-11］。

文章首先进一步分析了锁相环误差产生的原因，叙述了正序同步旋转坐标系与负序同步旋转坐标系下各分量的耦合关系，构造了解耦电路模块，消除因同步坐标变换产生的二倍频交流分量；并且加入滤波模块，滤除高次谐波分量，减少因谐波产生的锁相误差。

1 基于双同步坐标变换的锁相环问题分析

1.1 基于单同步坐标变换传统锁相环分析

电网三相电压可表示为us=［uaubuc］T，经过Clarke变换可得两相静止坐标系下电压分量，usαβ=［usαusβ］T再经过 Park变换可得两相旋转坐标系下电压分量 usdq=［usdusq］T。该变换过程如式（1）、式（2）所示。

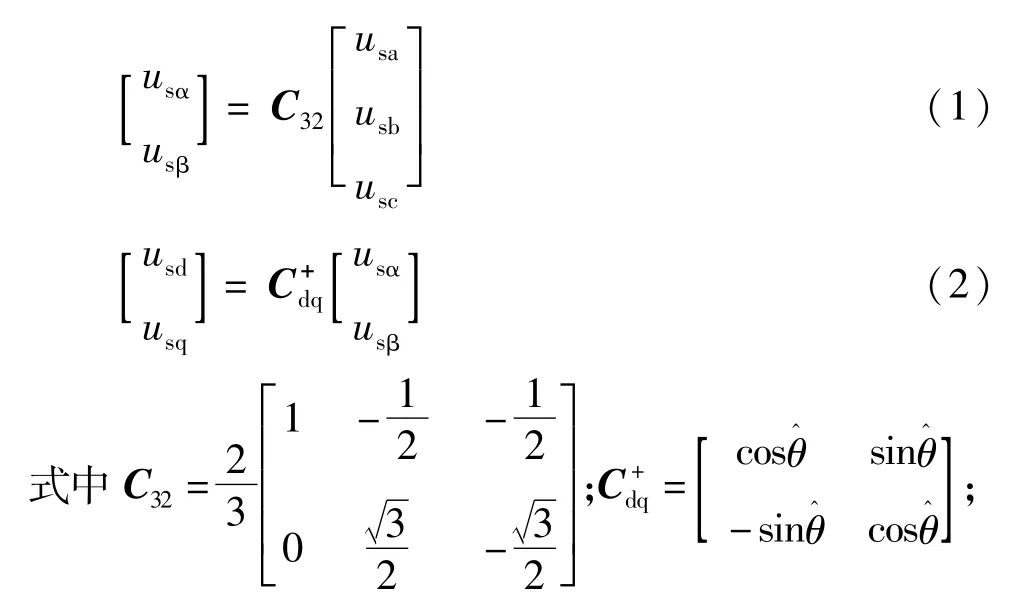
理想情况下，电网电压为三相对称电压，可以表示为：

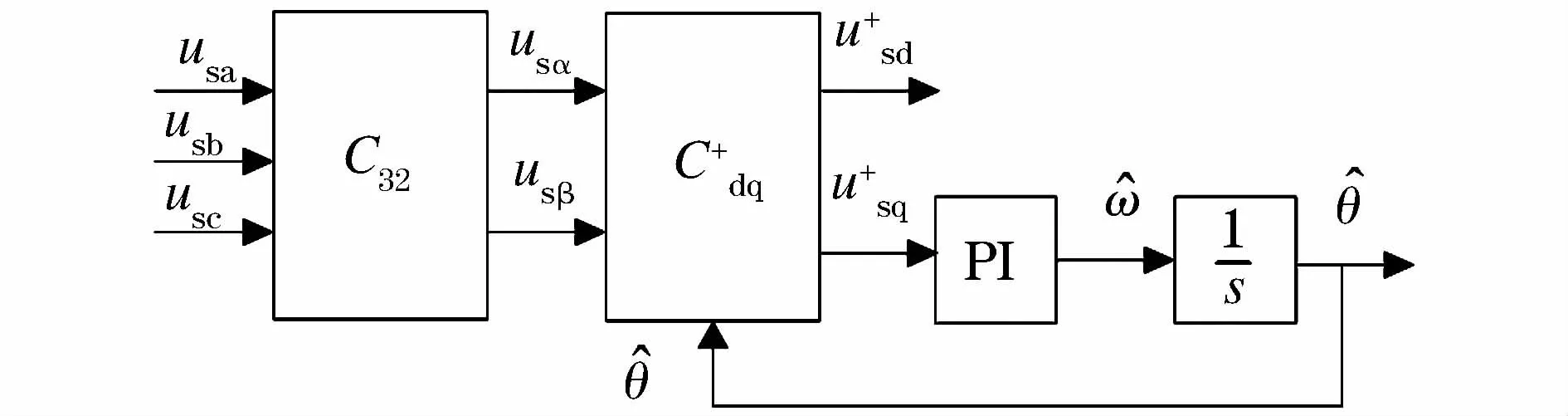
图1 基于同步参考坐标变换的锁相环结构图Fig.1 Configuration of PLL based on SRF

然而，对于实际电网，由于用电负荷不平衡、电网发生故障等原因，常伴随有电压暂降、频率突变、相位突变、谐波等问题，使得三相电网电压不对称。

（1）仅考虑基波分量时，电网电压可以分解为对称的正序、负序和零序三个独立的分量：

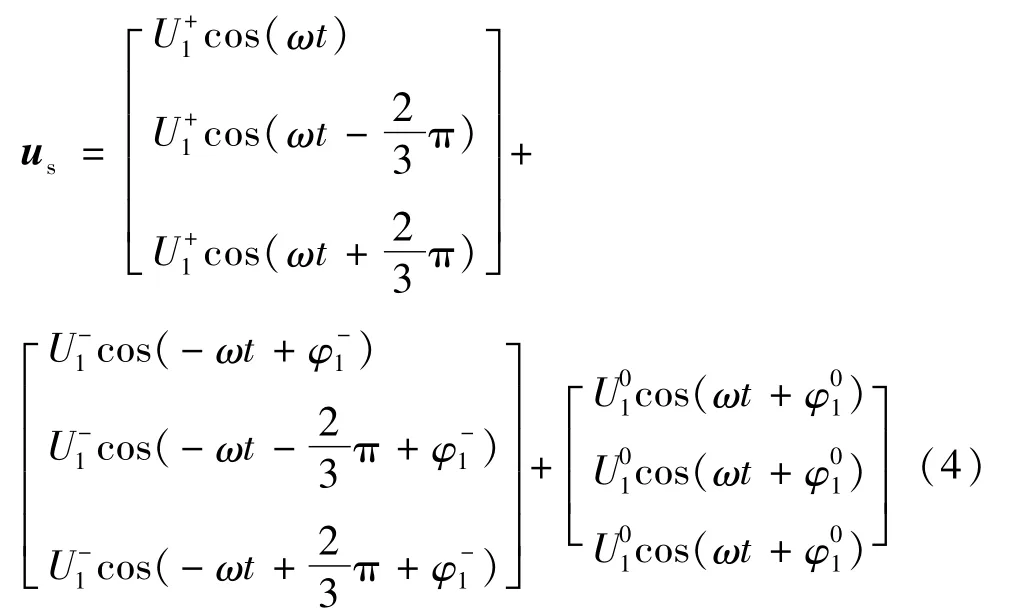
电网电压经过坐标变换可得：

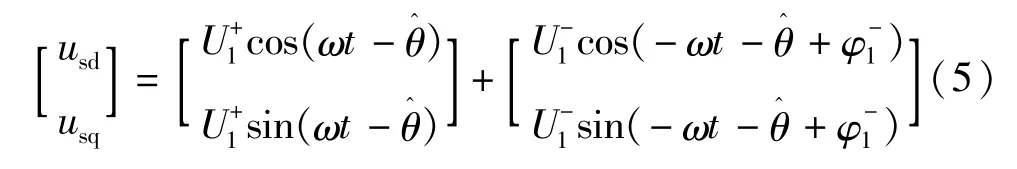
当锁相环精确锁定相位时，有ωt=θ＾，上式可化简为：

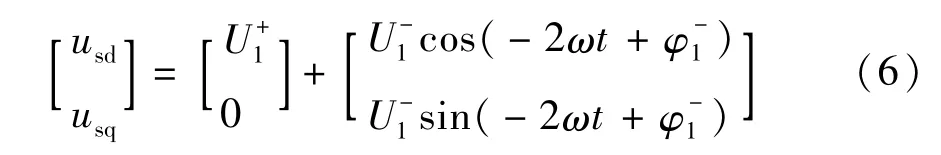
根据式（6）可知，基波正序电压分量映射到同步坐标系为直流量，基波负序电压分量变为二倍频正弦交流分量。

（2）当仅考虑电网电压谐波分量时，在三相坐标系下有：

分别为次谐波电压负序和零序分量的初相角。

对应在同步坐标系下的表达式为：

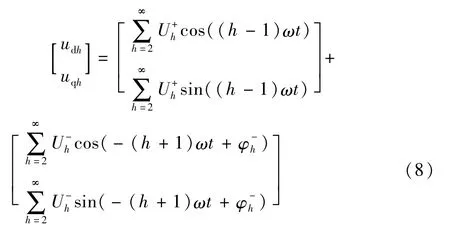
由式（8）可以看出，在正序同步旋转坐标系下，谐波正序分量次数减1，负序分量次数加1。

由以上分析可知，当电网电压处于非理想状态时，传统的SRF-PLL输出将出现2倍频分量与高次谐波，严重干扰锁相精度。

1.2 基于双d q坐标变换锁相环的分析

（1）仅考虑基波分量，对式（6）展开可得：

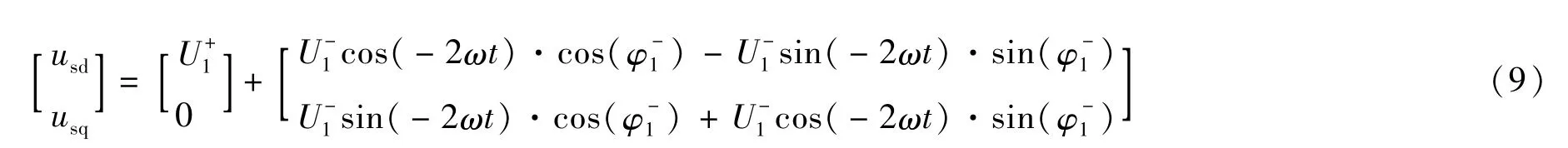
该表达式是在正序旋转坐标变换推导的，为了与负序旋转坐标变换的推导结果相区分，分别以来表示正序旋转坐标变换后的d轴与q轴分量。则式（9）可以写成：

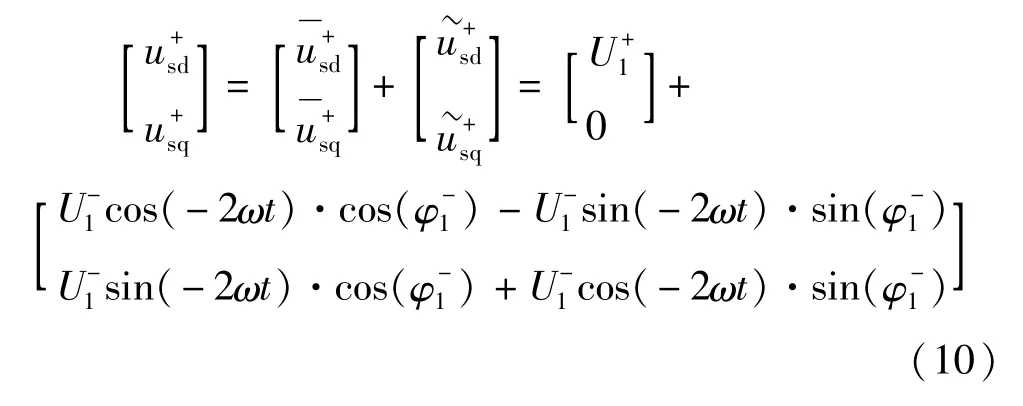
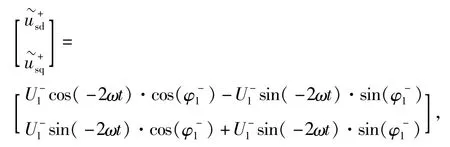
为电压经过正序旋转坐标变换后的二倍频交流分量。

（2）同理，由文献［5］，可以得到负序旋转坐标变换后的d轴与q轴分量，为：

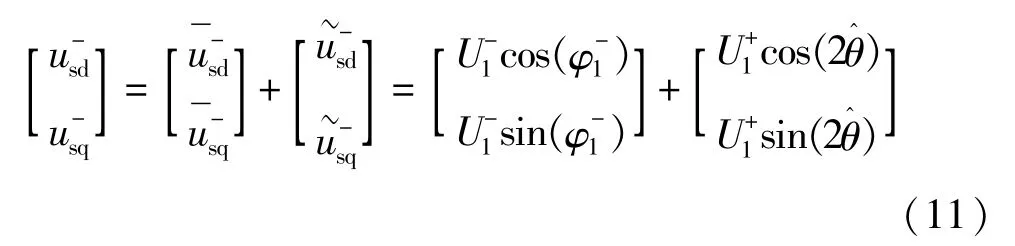
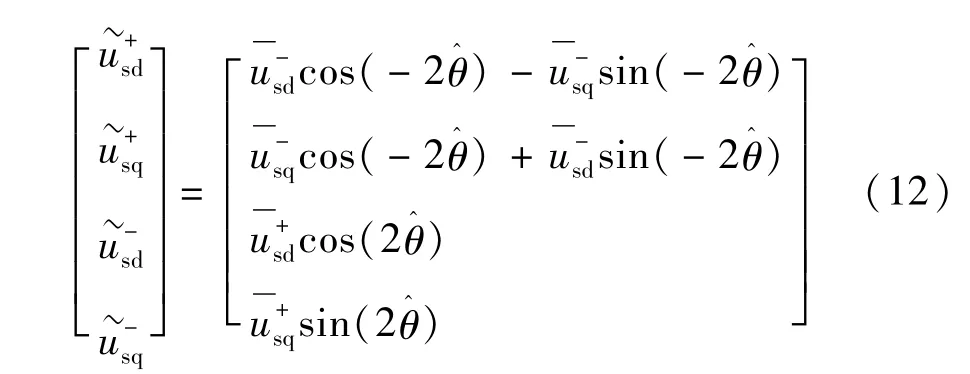
基于上述分析，文献［5］提出以下结构，以消除由于同步坐标变换引入的二倍频交流分量。如图2所示。

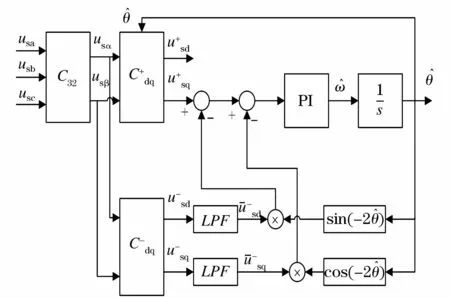
图2 基于双dq坐标变换的锁相环结构图Fig.2 Configuration of PLL based on DSRF

该方法是利用负序旋转同步坐标变换下的直流分量对正序旋转同步坐标下的交流分量进行补偿，可以在一定条件下实现相位的准确锁定，但也存在局限性。其局限性在于：

（1）仅考虑基波分量时，由式（10）可以看出，负序旋转同步坐标变换下的电压分量中含有二倍频交流分量要想得到直流分量如果仅通过增添滤波器的方式，对滤波器的性能有很高要求。如果减小滤波器的带宽，可较好地抑制电压谐波分量的影响，提高锁相精度，但动态响应时间将变长；如果增加滤波器的带宽，负序旋转同步坐标变换下的二倍频交流分量得不到有效衰减，反而可能予以放大并重新作用在正序旋转同步坐标变换下的电压分量上，增加相角检测的误差［12］；

（2）当考虑谐波分量时，由式（8）可以看出，正序旋转同步坐标变换下的电压分量u+sd、u+sq除了含有因坐标变换引入的二倍频交流分量外，还含有高次谐波分量，这无疑会影响锁相精度。

2 解耦滤波模块分析

根据式（12），不难发现正序旋转坐标变换下的二倍频交流分量可以表示为由负序旋转坐标变换下的直流分量产生的，而负序旋转坐标变换下的二倍频交流分量可以表示为由正序旋转坐标变换下的直流分量产生的。由此，可以确定两个旋转坐标系下各分量的耦合关系，该关系如图3所示。

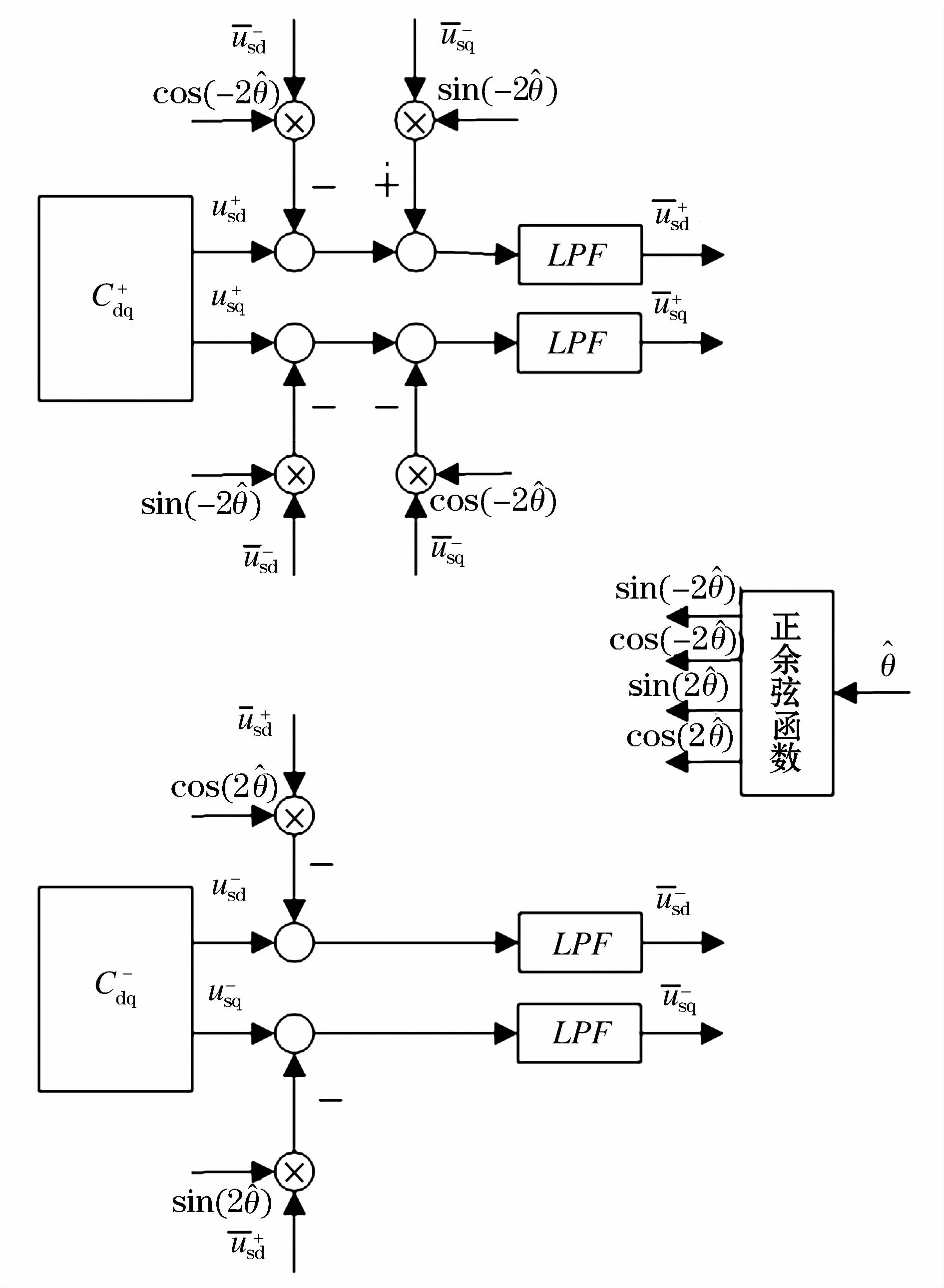
图3 解耦滤波模块结构图Fig.3 Structure diagram of decoupling and filteringmodel

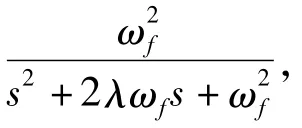
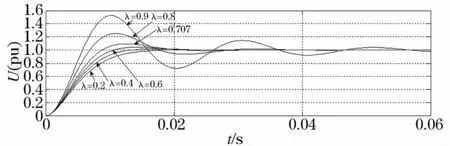
图4 系统在不同阻尼系数下的阶跃响应Fig.4 Step responses of system under different damping ratios

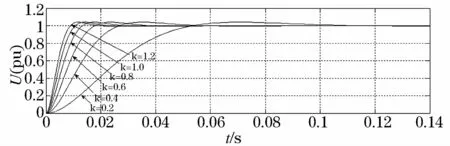
图5 系统在不同k值下的阶跃响应Fig.5 Step responses of system under different k values

3 基于双同步坐标变换解耦锁相环的提出

上文已经介绍了双同步坐标变换的解耦模块，通过该模块，可以有效地检测到电网三相不平衡电压的正序基波分量，然后构建基于双同步坐标变换解耦的锁相环，其结构图如图6所示。

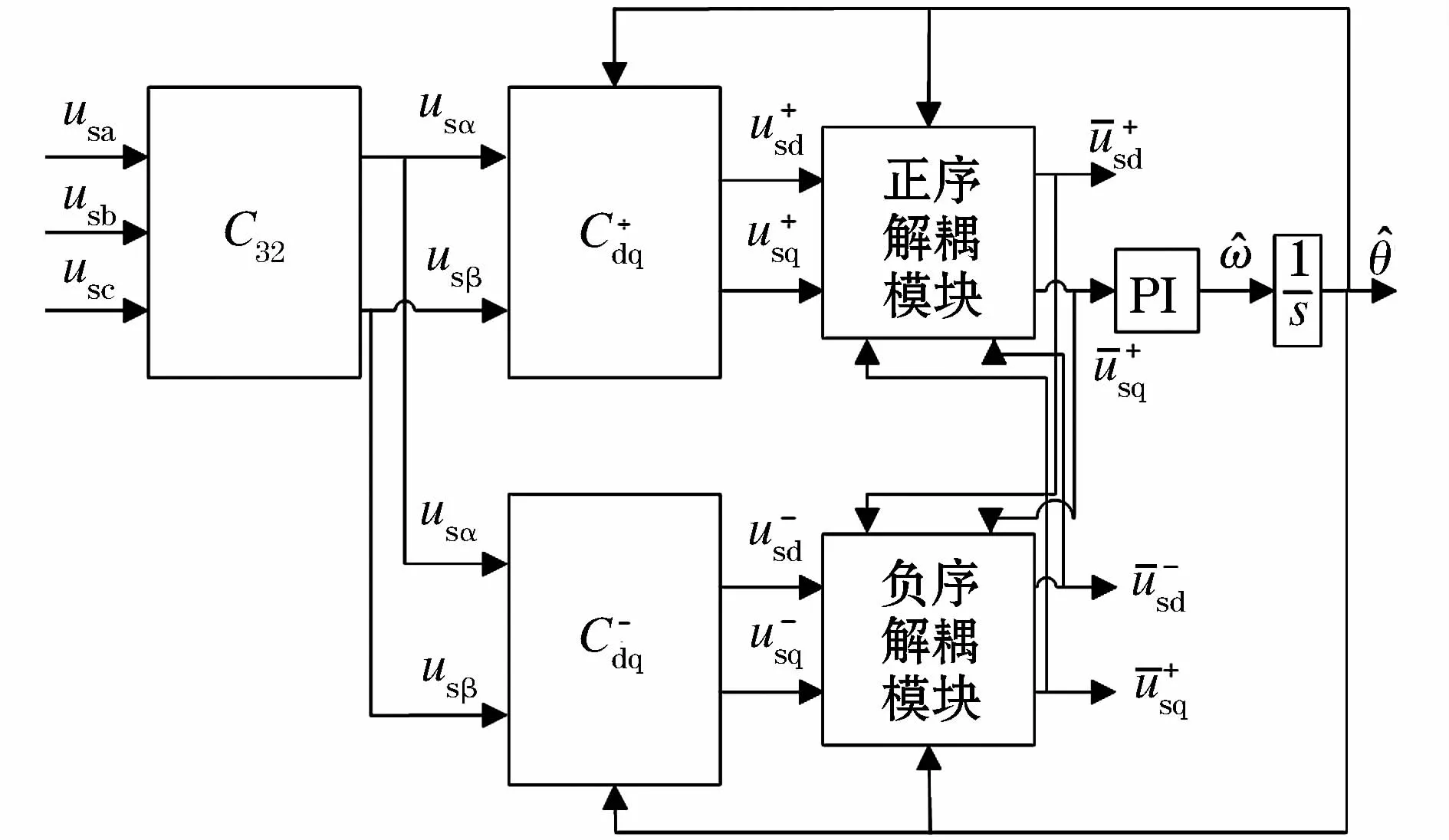
图6 基于解耦双同步坐标变换的锁相环结构图Fig.6 Configuration of PLL based on D-DSRF

如上图所示，电网三相不平衡电压经过Clarke变换得到两相静止坐标系下电压分量usα、usβ，然后分别经过正序Park坐标变换与负序Park坐标变换得到和以上四个分量在经过正负序解耦滤波模块得到和由前面所述被用做锁相环的输入，通过控制其值为0，来实现精确锁相的目的。

4 仿真分析

为了观察以上提出的解耦双同步坐标变换锁相环的性能，采用matlab/simulink进行仿真，并与文献［5］所提方法进行比较，仿真中三相电网电压幅值为220 V，频率为50 Hz，两种方法锁相环PI参数均为，kp=0.15，ki=1.2，二阶低通滤波器截止频率均设为20 Hz。

仿真结果分别给出了两种方法在电压跌落、频率突变、相位突变以及注入谐波等环境下的两种锁相环的对比分析，并观察了其动态性能与稳态性能。

4.1 三相电网电压不对称

此种情况选择输入电压暂降作为不平衡情况。设置故障前三相电压对称，即0.28 s～0.30 s时ua=220∠0°V；0.30 s～0.40 s时，a相电压跌落50%；0.40 s～0.45 s时，a相电压恢复到原来水平，如图7（a）所示。

图7 电压跌落时的两种锁相方法仿真对比Fig.7 Simulation comparison of two PLLswhile voltage dips

4.2 电网电压对称时频率突变

此种情况选择输入电压频率突变作为不平衡情况。设置故障前三相电压对称，即0.28 s～0.30 s时ua=220∠0°V；0.30 s～0.45 s时，a相电压频率由50 Hz突变到50.5 Hz，如图8（a）所示。

由图8可以看出，当电压出现频率突变故障时，解耦双同步坐标变换法与双同步坐标变换法都能在两个工频周期进入稳定状态（±2%），且均无明显超调，但是后者的检测结果中含有谐波。

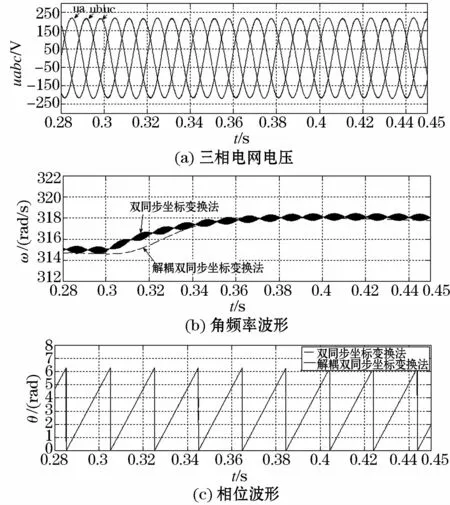
图8 电压频率突变时两种锁相方法仿真对比Fig.8 Simulation comparison of two PLLswhile frequency mutation

4.3 电网电压对称时相位突变

此种情况选择输入电压相位突变作为不平衡情况。设置故障前三相电压对称，即0.28 s～0.30 s时ua=220∠0°V；0.30 s～0.45 s时，a相电压相位突变60°，如图9（a）所示。

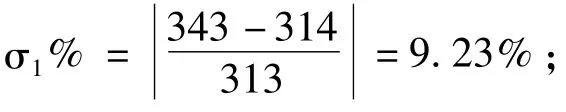
4.4 电网电压对称时注入谐波

此种情况选择注入谐波作为不平衡情况。设置故障前三相电压对称，即0.28 s～0.30 s时ua=220∠0°V；0.30 s～0.45 s时，a相电压注入10%的5次正序谐波分量，b相电压注入10%的2次负序谐波分量如图10（a）所示。

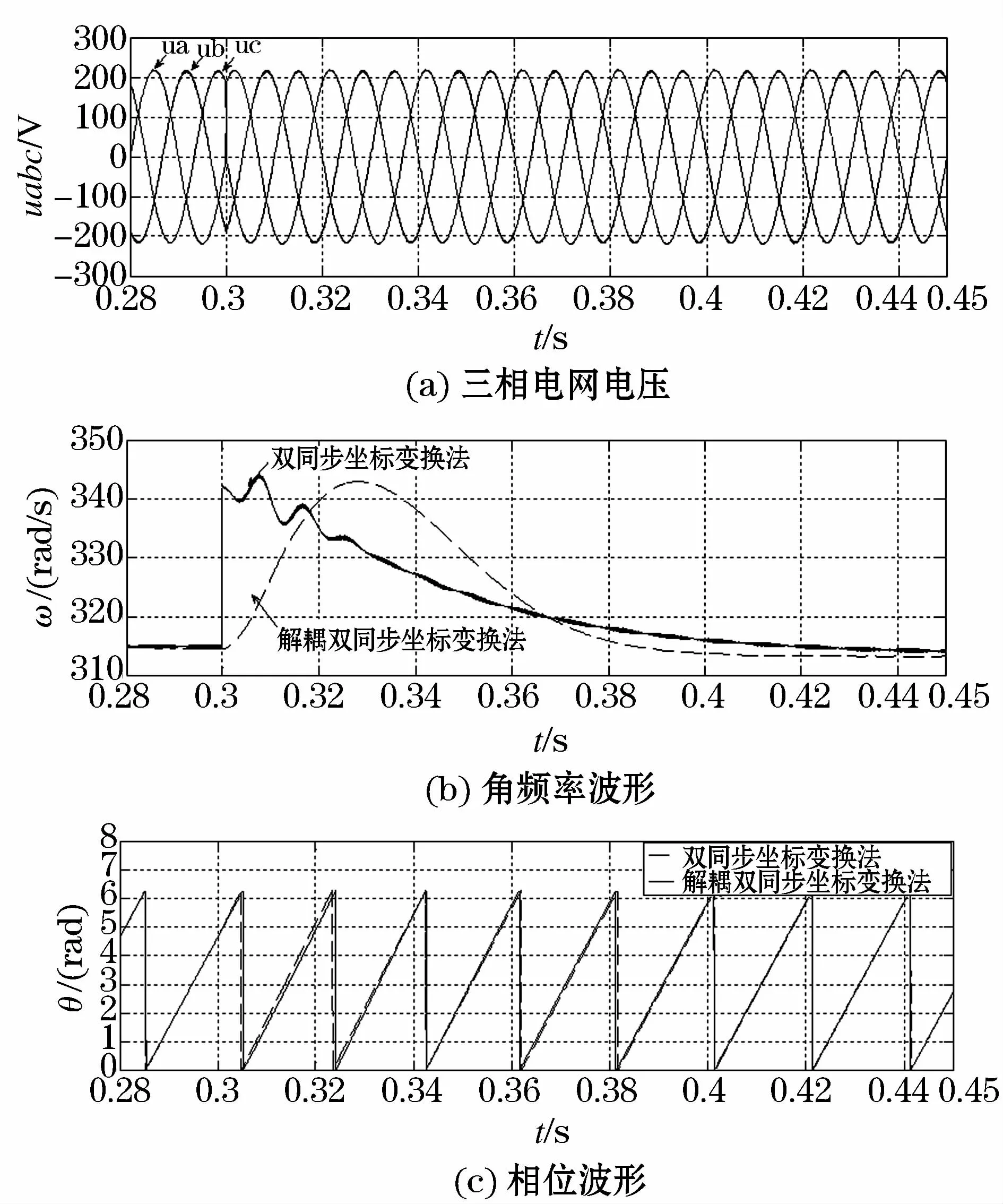
图9 电压相位突变时两种锁相方法仿真对比Fig.9 Simulation comparison of two PLLswhile phasemutation

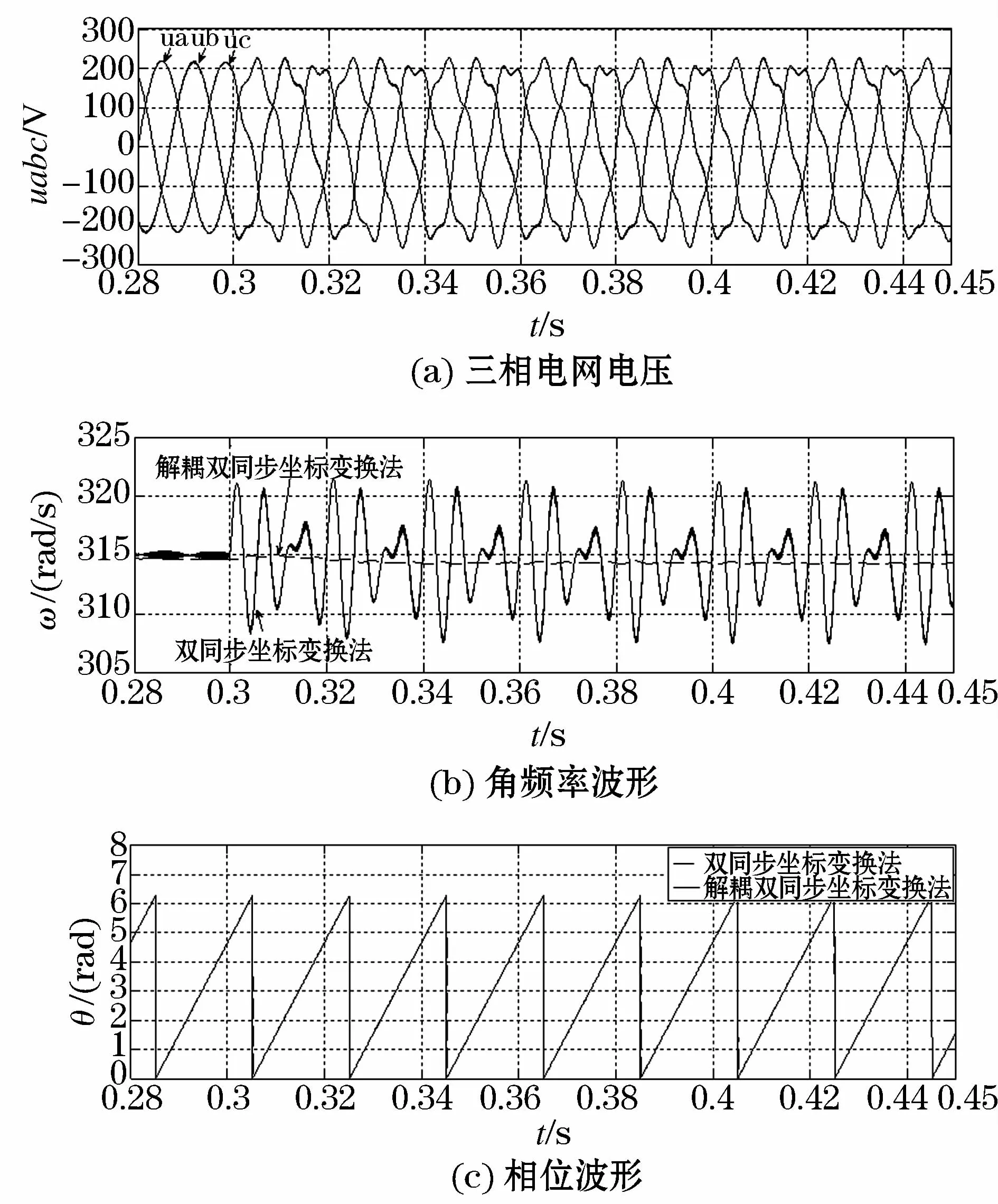
图10 注入谐波时两种锁相方法仿真对比Fig.10 Simulation comparison of two PLLs while harmonics injected

由图10可以看出，当电压出现相位突变故障时，解耦双同步坐标变换法只需要0.25个工频周期进入稳定状态（±2%）；双同步坐标变换法无法进入稳定状态，检测结果远超出允许波动范围，误差带为309 rad/s～321 rad/s，且含大量谐波，虽然通过采取降低二阶低通滤波器截止频率的措施可以抑制谐波，但无疑会大大降低系统的响应速度。

5 结束语

因实际电网电压中会出现各种不平衡故障，传统SRF-PLL在锁相的准确性跟快速性等性能并不理想。尽管文献［5］考虑了锁相过程中因正序同步坐标变换引入的二倍频交流电压分量，但忽视了负序同步坐标变换引入的二倍频交流电压分量以及更高次的谐波分量。本文通过提取负序同步坐标变换中d轴和q轴电压分量的直流分量，对正序同步坐标变换中d轴和q轴电压分量进行补偿；并且提取正序同步坐标变换中d轴和q轴电压分量的直流分量，对负序同步坐标变换中 d轴和q轴电压分量进行补偿，可以准确快速锁定基波正序电压相位。仿真结果表明，该方法能够快速准确的在各种不平衡故障下锁定电网的正序基波频率、相位等信息。