基于小信号模型的柔性直流输电网络运行稳定性研究*

2017-01-10饶雪刘开培杨洁秦亮

电测与仪表 2017年8期

饶雪，刘开培，杨洁，秦亮

（武汉大学电气工程学院，武汉430072）

0 引言

随着柔性直流输电工程的逐步建设，其系统稳定性必将成为影响电力系统安全稳定运行的重要因素，尤其在柔性直流输电网络中，随机性新能源的接入也带来了更多的小扰动因素［1］，小扰动会影响系统的运行稳定性。因此对柔性直流输电网络进行小信号稳定性分析，判断系统在指定的运行方式下是否稳定，具有重要的意义。

对柔性直流输电网络进行小信号稳定性分析时，重点在于柔性直流输电网络的小信号建模以及推导静态稳定性判据。文献［2］根据换流站的外特性直接将换流站简化；文献［3］用状态空间平均法将换流站等效为理想变压器；文献［4］未考虑直流输电线路中的电容电感效应对系统小信号稳定的影响；文献［5］采用模态分析研究多端柔性直流输电系统小信号稳定性，未分析参数优化；文献［6］采用传递矩阵分析方法研究与弱交流系统互联的柔性直流输电系统小信号稳定极限。这些研究均取得了一定成功，但在模型构造及稳定性优化问题上存在欠缺。

本文针对以上研究问题，推导更适用于柔性直流输电网络的小信号模型，通过状态空间法及李雅普诺夫稳定性判据分析柔性直流输电网络小信号稳定性判据，以三端柔性直流输电网络为算例，判断在特定工作点下柔性直流输电网络的小信号稳定性，并进行PI参数优化仿真，最后用参与因子验证优化规律，为提高系统的静态稳定性提供依据，便于柔性直流输电网络实际工程应用中控制器设计的研究。

1 柔性直流输电网络小信号建模

柔性直流网络的小信号模型主要包括三个部分：电压源型换流站、控制系统和直流输电网络。

1.1 电压源型换流站的小信号模型

电压源型换流站的线性化方程基于dq0坐标系下的准稳态模型，如图1所示［7］。该模型表示，在理想条件下，换流器工作在稳态工况时交流系统基波电压、电流与直流电压、电流间的关系。

图1 电压源型换流站的准稳态模型Fig.1 Quasi steady statemodel of VSC-converter

在满足一定假设条件下［8］，电压源型换流器在dq0坐标系下的准稳态模型为（d轴超前q轴）：

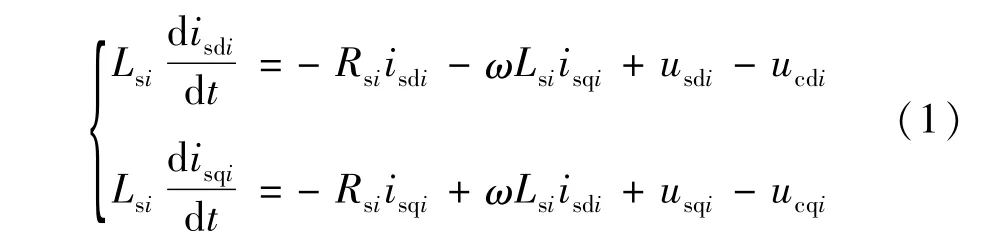
其中，在第i个换流器中，Lsi为联结电抗器阻值，Rsi为等效电阻阻值，usdi、usqi为交流电源出口侧电压的dq分量，ucdi、ucqi为换流器出口侧电压的dq分量，isdi、isqi为换器出口侧电流的dq分量。设第i个换流器正负极直流母线间的电压为Udi，由于忽略换流站损耗，故有：

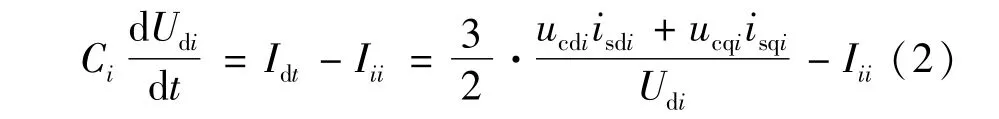
式中Ci为换流器直流侧出口处电容；Iii为直流传输线路上的电流。

设isdi0为静态工作点的电流，则扰动后的交流侧电流d轴分量为：

同理，给其他系统参数增加扰动量，代入式（1），并在二次项处进行泰勒级数展开，略去高阶无穷小项，可得换流站的线性化模型：

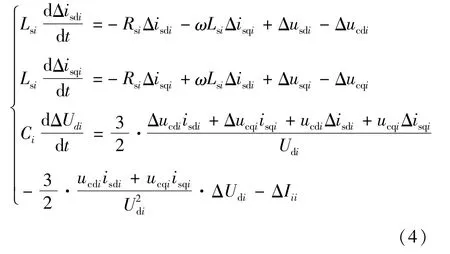
1.2 换流站控制系统的小信号模型

柔性直流输电在交流系统平衡条件下的直接电流控制是目前广泛采用的控制方法，此种控制方式分为内环电流控制和外环电压控制［9］。

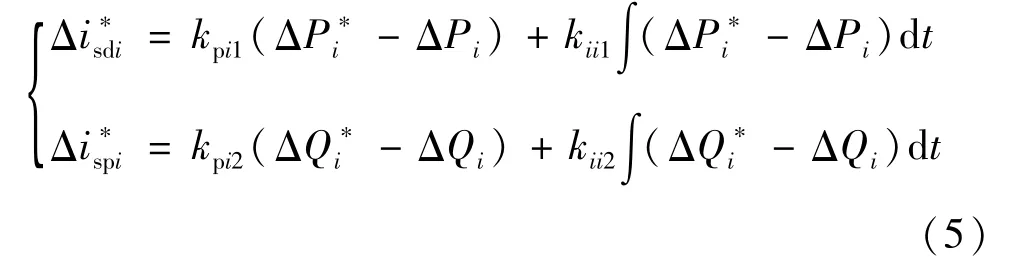
大多数换流站外环采用定有功功率、定无功功率控制［10］，此时将外环控制器线性化后有：式中Δ表示扰动量；isdi*、isqi*为外环控制输入给内环的有功、无功电流控制指令；Pi*、Qi*为系统级控制器给定的有功、无功参考信号；Pi、Qi为系统运行时的交流侧实际有功、无功功率；kpi1、kii1为定有功功率控制端外环PI调节器参数；kpi2、kii2为定无功功率控制端外环PI调节器参数。

为微分方程组计算方便，令：

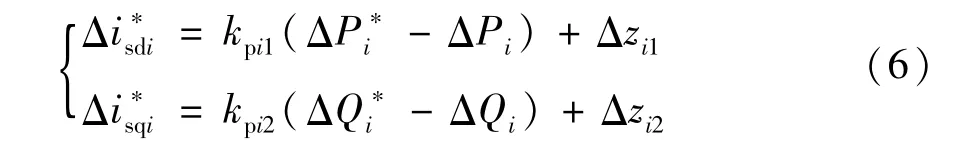
控制目标扰动量的线性化方程：

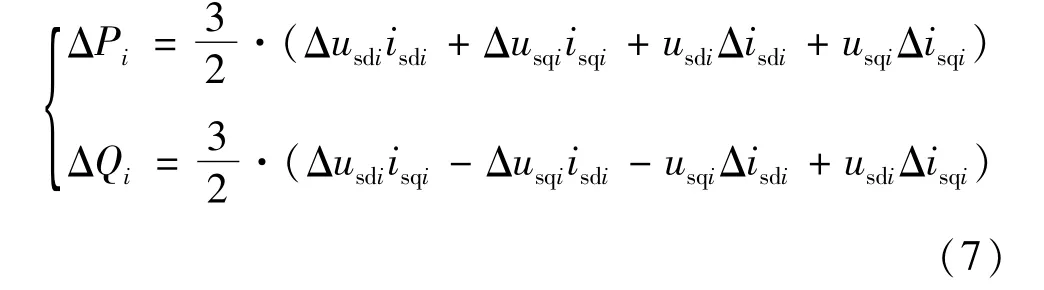
将式（7）代入式（5）可得当采用定有功功率、定无功功率控制时电压源型换流器外环控制器的线性化模型。

当采用直接电流控制时，将内环控制器线性化后有：

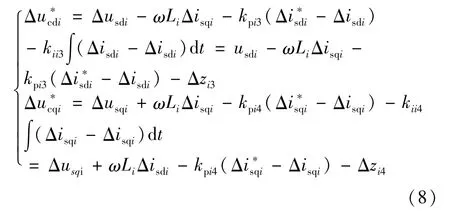
式中 kpi3、kii3为有功控制端内环PI调节器参数；kpi4、kii4为无功控制端内环PI调节器参数。

同理，为微分方程组计算方便，则式（8）可简化为：

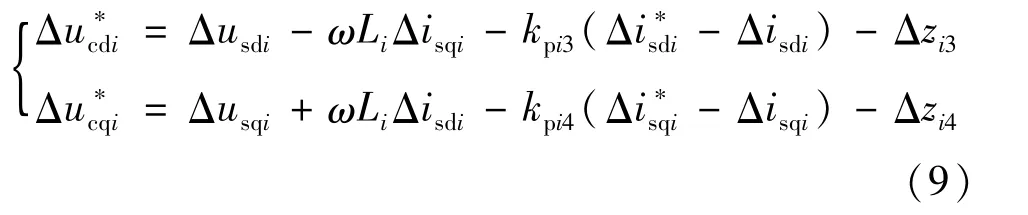
对于平衡节点，需要为柔性直流电网提供电压基准和支持，故应采用定直流电压及定无功功率控制。此时将外环控制器线性化后有：

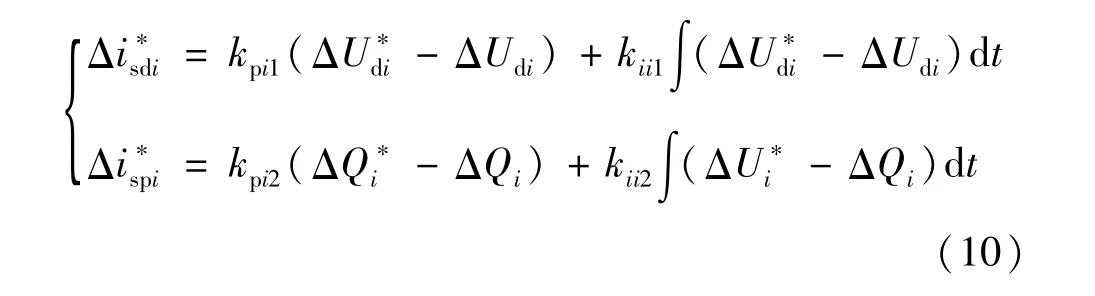
式中Δ表示扰动量；Udi*为系统级控制器给定的直流电压参考信号。

同样的，式（10）可简化为：

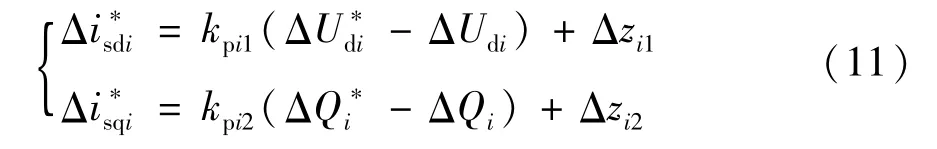
内环控制器的线性化方程如式（9），联合式（11）可推算出在定直流电压、定无功功率控制下，第i个电压源型换流器的线性化方程。

1.3 直流输电网络的小信号模型

在柔性直流输电网络中，由于换流站出口处直流母线的长度远小于输电线路长度，在直流输电线路模型的搭建时，忽略直流母线的长度，并将输电线路进行π型等效，直流线路部分模型如图2所示。

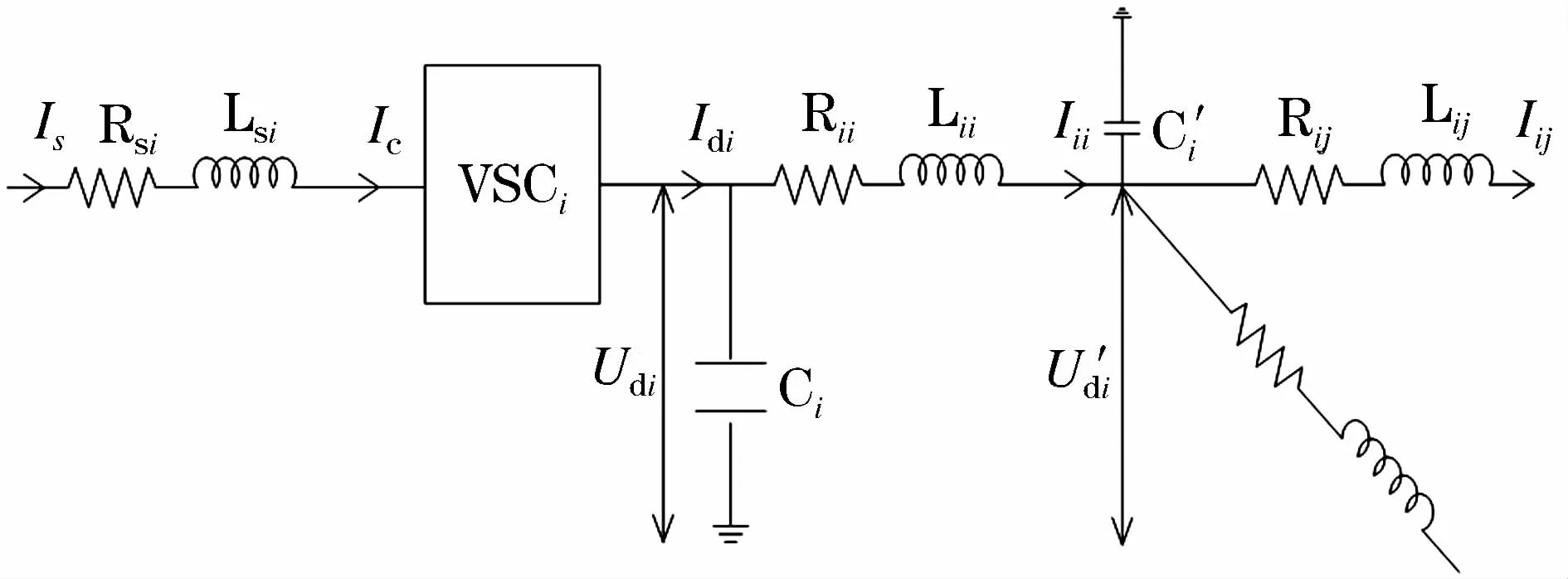
图2 直流线路等效模型Fig.2 Equivalentmodel of DC line

图中，Rij、Lij表示 i、j两换流站间输电线路的等效电阻和电感；C表示节点处分支输电线路π型等效后的电容；Ci表示换流站出口处直流电容，当输电线路不是很长时，Ci≫C，故可以忽略这一端的等效电容；Udi为第i个换流站出口处电压；为节点处的电压；Idi表示第 i个换流站出口处电流；Iij表示 i、j两换流站间输电线路上的电流，由i到j为正。

则直流网络的小信号模型为：

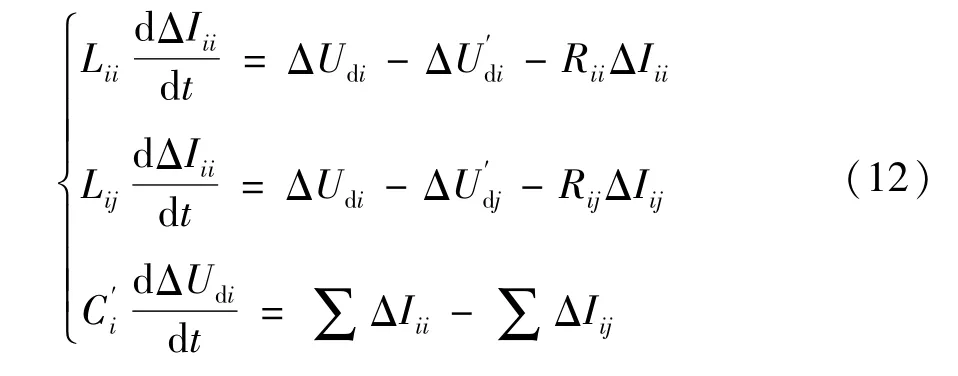
1.4 小信号模型的仿真验证

通过将柔性直流输电网络的状态方程在平衡点附近线性化得到了网络的小信号模型，由于不能判定该线性化方法是否合理，故以两端系统为例如图3所示，通过电磁暂态仿真与小信号模型线性仿真对比，验证小信号模型的正确性［11］。

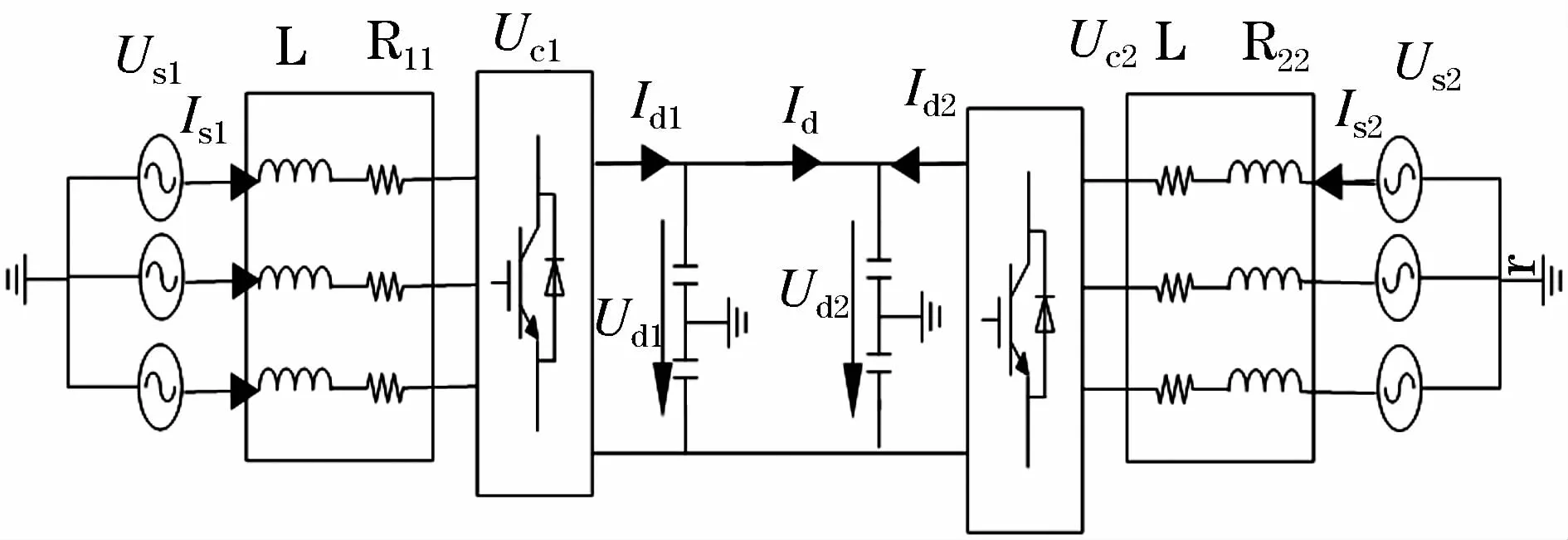
图3 两端柔性直流输电系统Fig.3 Double ended VSC-HVDC transmission system

在这个两端柔性直流输电系统中，整流站采用定有功功率、定无功功率控制，逆变站采用定直流电压、定无功功率控制，在静态工作点一致的前提下，设置整流侧的有功功率产生小扰动，冲击2 MVA，时间持续0.1 s，将两个模型的仿真结果进行对比，如图4～图7所示。

在图4～图7中，上方的图表示电磁暂态仿真中交流侧电流等物理量的仿真结果，下方的图表示小信号线性仿真中中交流侧电流小扰动量的仿真结果。通过对比四组仿真波形可知，变化的趋势和幅值基本一致，表明柔性直流网络的小信号数学模型是正确的。

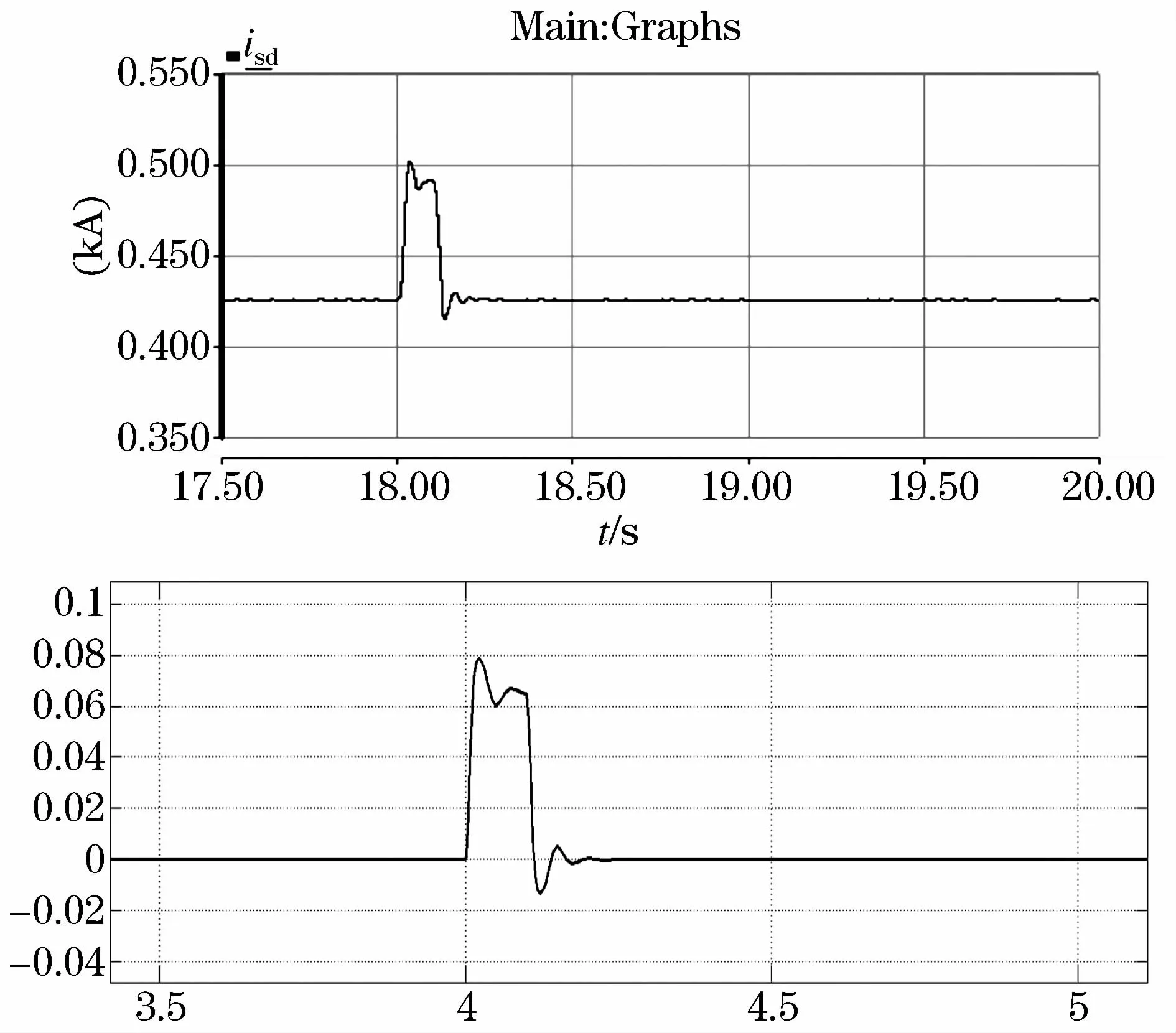
图4 i sd1与Δi sd1的比较图Fig.4 Comparison diagram between i sd1 andΔi sd1

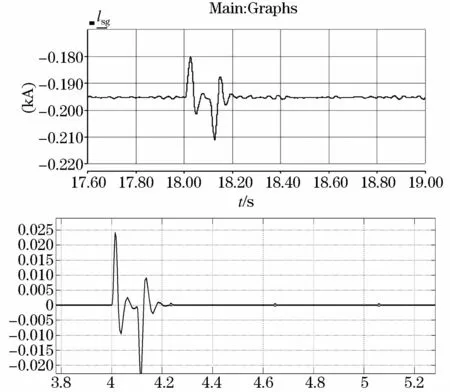
图5 i sq1与Δi sq1的比较图Fig.5 Comparison diagram between i sq1 andΔi sq1

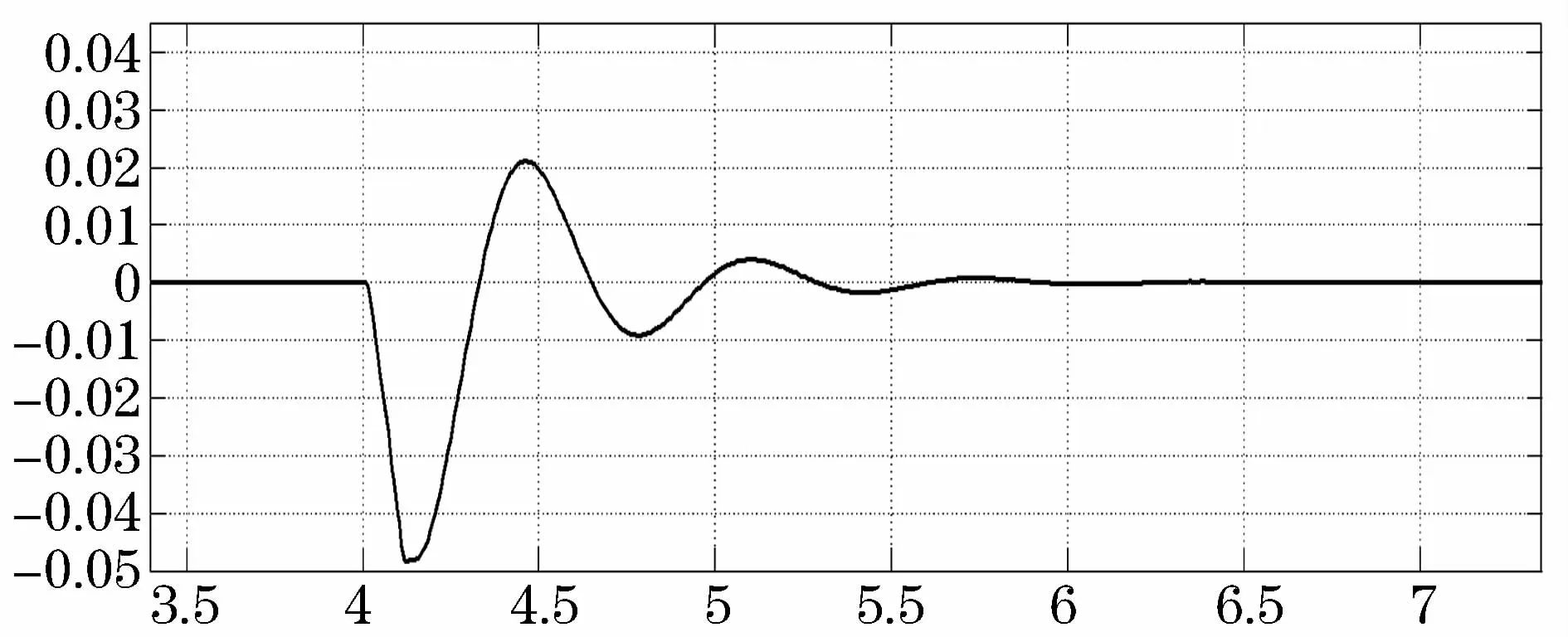
图6 i sd2与Δi sd2的比较图Fig.6 Comparison diagram between i sd2 andΔi sd2

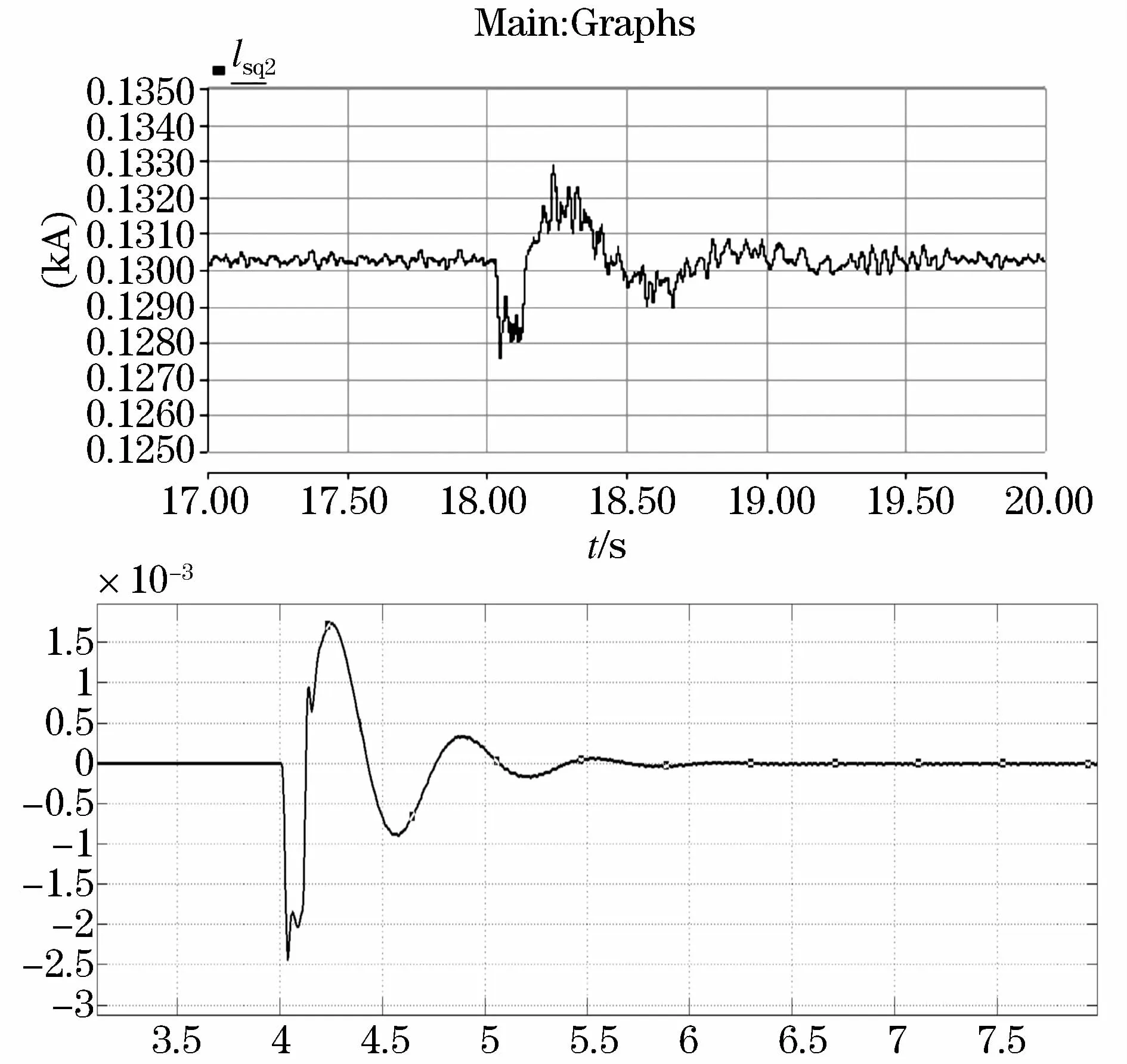
图7 i sq2与Δi sq2的比较图Fig.7 Comparison diagram between i sq2 andΔi sq2

2 小信号稳定性分析法

根据状态空间法，有状态方程式（13）：

动态系统的特征值即为状态矩阵A的特征值，可由式（14）求解。

如果动态系统有n个状态变量，那么式（14）存在n个独立解，这些解即为该系统的特征值。线性系统在工作点附近的小信号稳定性可有李雅普诺夫稳定性第一准则进行判断，根据具体判据可知，当线性系统所有特征值的实部均为负时，该系统才为渐近稳定。矩阵A的最小特征值|λ|min表征该点小扰动稳定性的裕度，即|λ|min越大，系统的小信号稳定性就越强［12］。

当计算出左右特征向量后，可根据式（15）求出对应的参与因子pki：

|pki|是一个系统指标，表示第k个模式与第i个状态变量之间的可观性及可控性。|pki|值越大，表明该状态变量对该种模式具有更强的影响性［13］。

将电压源型换流站、控制系统和直流输电网络的小信号模型结合起来，可以得出柔性直流输电网络的线性化状态方程组，整理后有：

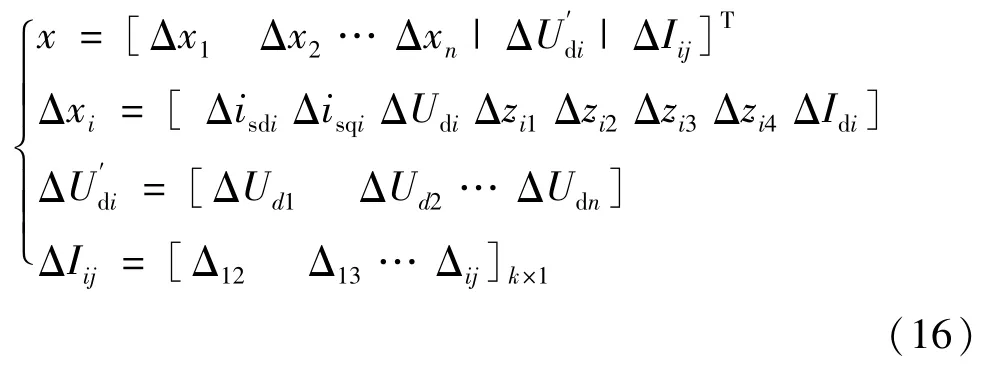
在式（13）中，矩阵A的构成为：

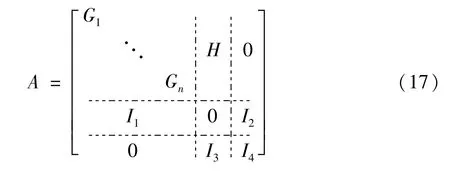
因此柔性直流网络小信号稳定性分析的判据为：若状态矩阵A中所有特征值的实部均为负值，则该柔性直流输电网络具有小信号稳定性。

3 算例分析

本节以典型三端柔性直流输电环网为例研究其小信号稳定性，电路拓扑结构如图8所示。

此三端柔性直流输电环网中换流站1采取定有功功率和定无功功率控制，换流站2采取定直流电压和定无功功率控制，换流站3采取定有功功率和定无功功率控制，控制量给定参数和部分系统参数如图所示。根据潮流分布计算三端柔性直流输电环网中各变量的稳态初始值如表1所示。

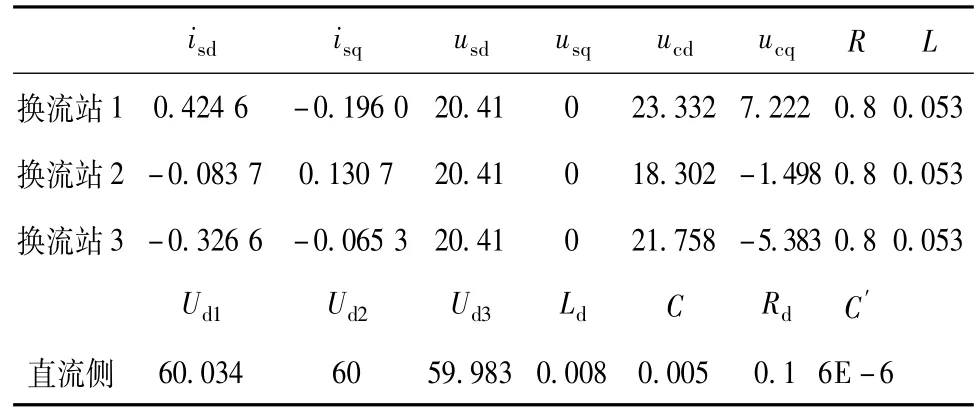
表1 三端柔性直流输电环网稳态值Tab.1 Three-terminal VSC-HVDC ring network steady state value

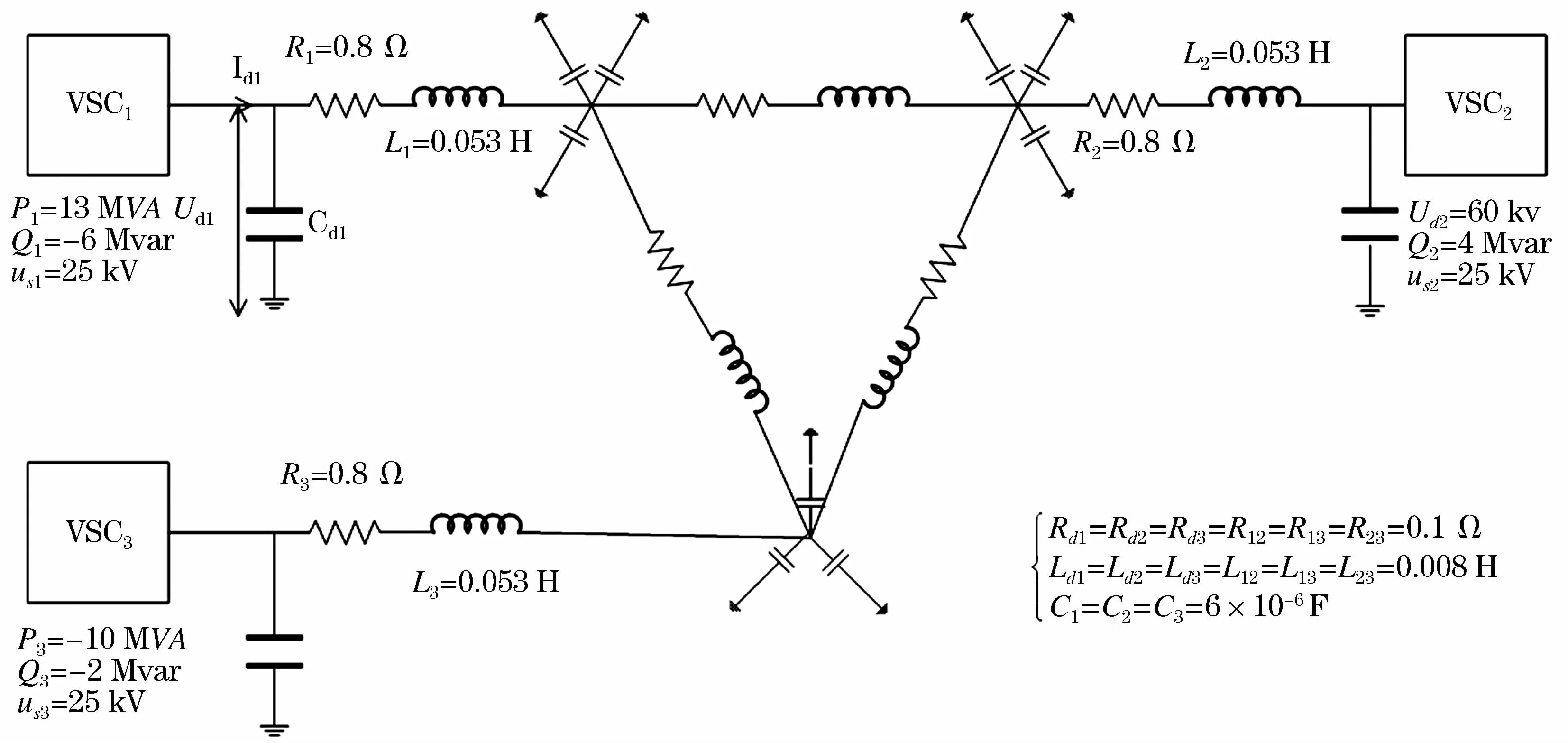
图8 三端柔性直流输电环网电路拓扑结构Fig.8 Circuit topology structure of three-terminal VSC-HVDC ring network

3.1 小信号稳定性判断

利用第二节介绍的状态空间法对三端柔性直流输电网络的小信号模型进行整理如下：

该模型有3个节点，6条支路，故此状态矩阵A是一个大小（30×30）大小的矩阵，根据第1节推导的小信号模型，算出矩阵A中的各元素。

设换流站 1的 PI参数为 kp1、kp2、kp3、kp4、ki1、ki2、ki3、ki4；换流站 2的 PI参数为 kp5、kp6、kp7、kp8、ki5、ki6、ki7、ki8；换流站 3的 PI参数为 kp9、kp10、kp11、kp12、ki9、ki10、ki11、ki12，此时设置 PI参数为：

若要分析三端柔性直流输电环网的小信号稳定性，需要求解其状态矩阵的特征值，求解可利用matlab程序实现，求得的特征值结果如表2所示。

观察表2，30个特征值的实部均为负，根据李雅普诺夫稳定性定义，可知系统具有静态稳定性，且|λ|min，出现在第28号特征值。能表征在该平衡状态下小扰动稳定性的裕度，即|λ|min越大，系统的小扰动稳定性就越强。

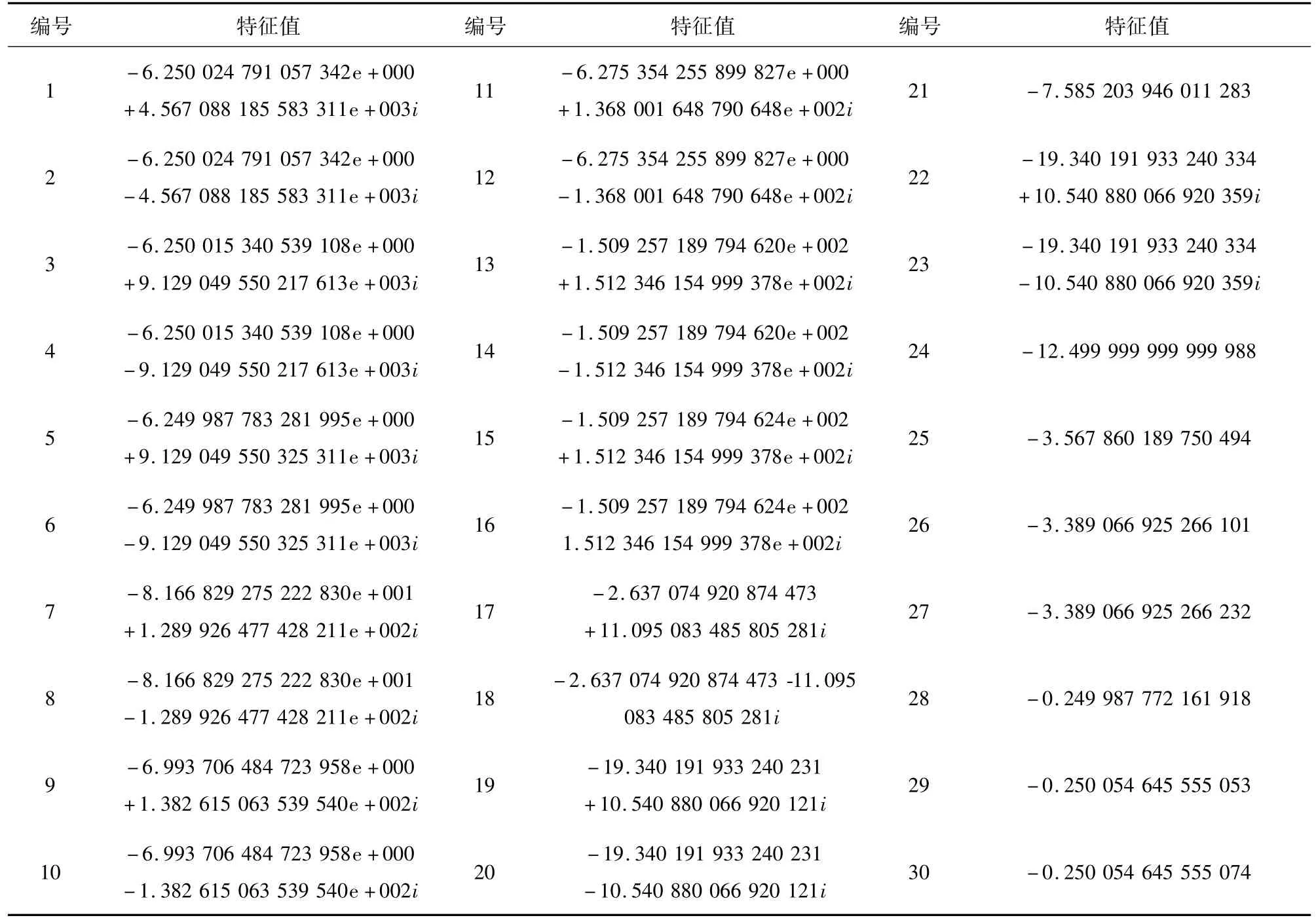
表2 特征值结果Tab.2 Results of characteristic value

3.2 PI参数优化

影响系统小信号稳定性的因素很多，若需提高系统的静态稳定性，即需要增大|λ|min，最常见措施是做PI参数优化［14］，因此首先需要了解PI参数与特征值之间的关系，故做如表3所示探究：

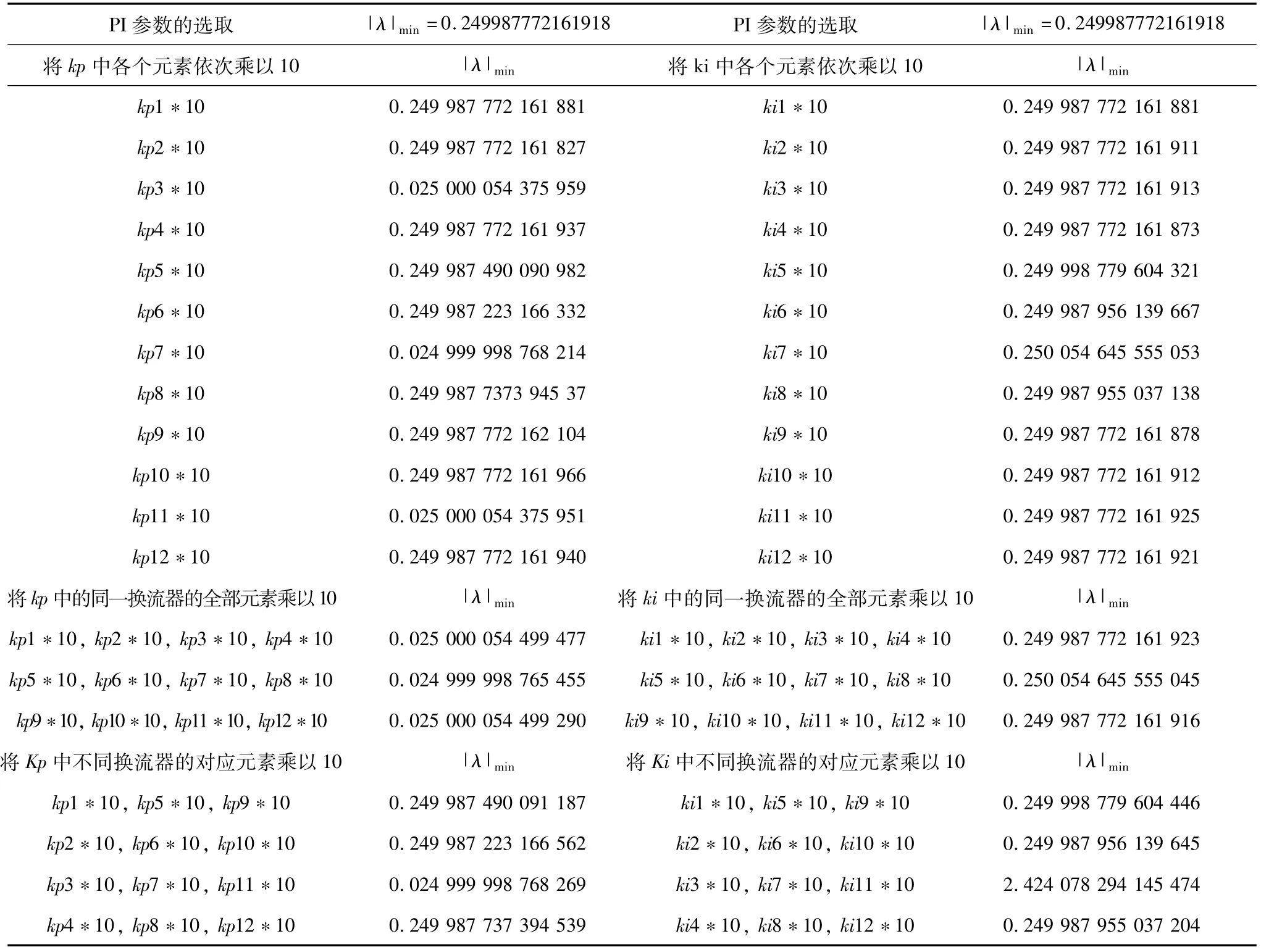
表3 PI参数与特征值的关系Tab.3 Relationship between PI parameters and characteristic values

根据表3的仿真结果，总结在此种情况下PI参数与特征值的关系，可以得到如下规律：

（1）将 kp3、kp7、kp11分别乘以 10，|λ|min均变小，其值均约为原值的十分之一，其他kp值变化对特征值影响不大；

（2）将某一换流站的kp值全部乘以10，|λ|min均变小，其值均约为原值的十分之一；

（3）将 kp3、kp7、kp11同时乘以10，变小，且减小程度与这三个元素依次乘以10的程度相同；

（4）将 ki的各元素依次乘以10，|λ|min对特征值的影响均不大；

（5）将某一换流站的ki值全部乘以10，对特征值的影响不大；

（6）将 ki3、ki7、ki11同时乘以 10，|λ|min变大，其值约为原值的10倍。

若将 kp3、kp7、kp11同时乘以100、1 000、1 0000，特征值均变小，且变化程度与kp元素的变化存在比例关系。将 ki3、ki7、ki11依次乘以 100，|λ|min=3.399 789 329 825 847；若将 ki3、ki7、ki11依次乘以1 000，|λ|min=3.416 193 571 243 017；将 ki3、ki7、ki11依次乘100 000，|λ|min=3.417 795 291 270 069。由此可得特征值的变化与kp、ki元素均有关系，增大kp3、kp7、kp11会使最小特征值变小，增大 ki3、ki7、ki11会使最小特征值变大，且kp参数的可控性较强。

对于上述规律，进行参与因子验证，编写参与因子程序，将仿真结果的参与因子由大到小排列，由于直流网络的参数设定除了与系统的稳定性有关，还需考虑其他因素，故此处略去直流网络的状态变量，取剩下排列前六的因子如表4所示。

由参与因子可知，忽略直流网络状态变量的影响，状态变量 Δisd1、Δisd2、Δisd3、ΔZ7、ΔZ3、ΔZ11对最小特征值的影响较大，此六个状态变量均与内环控制的d轴控制参数有关，故可验证上文的规律分析。但Δisd2、Δisd2、Δisd3除了包含 kp3、kp7、kp11也包含其他kp参数，对于kp参数的具体验证此处还很欠缺，今后需更加精确的选择状态变量。