基于伪信号起始时刻法代数求解的变电站局放定位*

王振浩，熊毅，龙超，庞丹，李国庆

（1.东北电力大学 电气工程学院，吉林吉林132012；2.长春供电公司，长春130033）

0 引 言

电力设备绝缘的缺陷在短路、雷击或者开关瞬变操作等诸多外在压力下可能会诱发事故［1-2］。所以对设备的绝缘系统状态的持续评估和诊断尤为重要，这既有助于系统的连续性风险评估，也利于绝缘故障的早期发现［3-4］。

局部放电监测是一种对绝缘系统状态评估的非破坏性的高灵敏性的诊断方法，是及时发现电力设备绝缘缺陷、避免绝缘击穿故障的有效手段［5-6］。局放定位有助于制定更有针对性的检修处理方案，减少停电时间，提高检修效率［7-9］。

目前应用于局放检测定位方法主要有超声波法、脉冲电流法和UHF超高频电磁波法等［10-11］。其中超声波易受各种背景噪声的干扰，并且在空间衰减快、波速不稳定，只适合于小范围的准确定位；脉冲电流法容易受到现场各种电磁信号的干扰，降低了检测的灵敏度，不适合用于在线监测；局放时辐射出的0.3 GHz～3 GHz电磁波，其频谱特性与局放源的几何形状以及放电间隙绝缘强度有关，由于其检测频段高、检测频带宽，可以有效地避开现场的各种电气干扰，通过传感器接收局放辐射的超高频电磁波，实现局放的检测与定位，测量过程中确定UHF信号的起始时刻关系到整个局放检测的精确程度［12-15］。

本文采用UHF超高频电磁波法进行局放的检测与定位：在信号的采集过程中，对传统的能量累积函数进行改进，避免了传感器接收到现场的各种噪声信号而导致信号起始时刻的误判断；以伪信号起始时刻法对局放源与传感器坐标建立非线性方程组，并用静态伪距方程代数求解法进行代数直接求解，避免了迭代算法因对初值的高要求而导致的计算偏差。最后经现场测试验证了伪信号采集时刻法与静态伪距方程代数求解法结合在局放定位中的合理性与有效性。

1 电磁波信号的检测与处理

在采用UHF电磁波信号进行局放检测的过程中，信号起始时刻的精准程度决定了局放源定位的精准性［16-17］。用传感器采集局放辐射出的电磁波信号，在改进的能量积累函数下能够更精确的确定局放电磁波信号的起始时刻。局放辐射的UHF电磁波信号典型波形如图1所示，其中t为传感器采集到电磁波信号的时刻，是局放检测和定位的关键点之一。

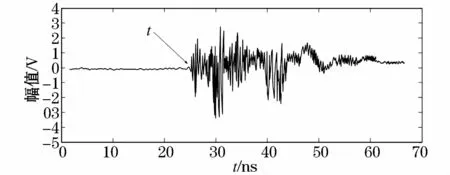
图1 UHF波形图Fig.1 UHF waveform

1.1 能量积累函数

能量累计曲线Si见式（1），其中xk的定义为信号波上第 k个点的电压值，i是每个波形记录的点数：

局放发生时辐射的UHF信号的幅值远大于背景噪声。经过能量积累，局放辐射的UHF信号在能量积累函数上对应一个拐点，即UHF信号传播至传感器的时刻［18］。由于传感器接收到的信号中包含了现场的各种噪声信号，所以在局放电磁波信号到达之前能量积累曲线也会出现拐点，这会导致信号起始时刻的误判断。

1.2 改进的能量积累函数

对式（1）的能量积累函数进行改进修正：

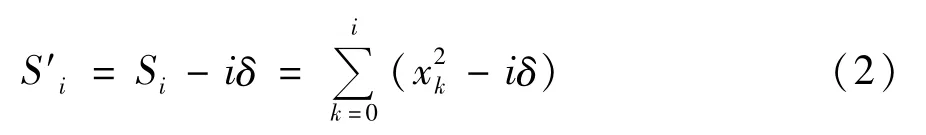
在式（1）的基础上引入一个修正量δ，其中修正量δ取决于接收信号的总能量SN以及接收信号的总采样数N，其关系式为：

改进能量积累函数的曲线见图2。经过改进的能量积累曲线在接收到局放信号前持续下降，采集到局放电磁波信号后出现拐点。这样改进的能量曲线有一个最低点，而这个最低点就对应了局放电磁波信号的起始时刻。避免了传感器接收到噪声信号而发生的误判。

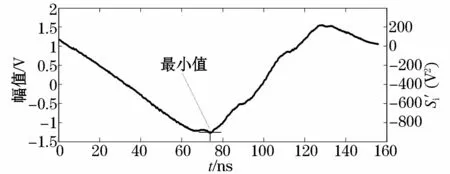
图2 改进能量积累曲线Fig.2 Improved energy accumulation curves

2 局放定位空间模型建立

图3所示，在检测范围内安装了i个坐标已知的传感器接收局放的电磁波信号，PD为具体坐标未知的局放源，传感器Si到局放源的测量距离为Ri。可以得到i个相交于局放源的球面函数，这样就可以得到一组反应局放源和i个传感器的空间位置关系的非线性方程组［18］。局放源坐标（x，y，z）同时满足几个非线性方程组，即为球面函数的交点。

2.1 绝对时间法

假设局放发生的时刻是已知的，局放定位的问题在数学上就成为一个绝对时间的求解问题，如图4所示［19］。

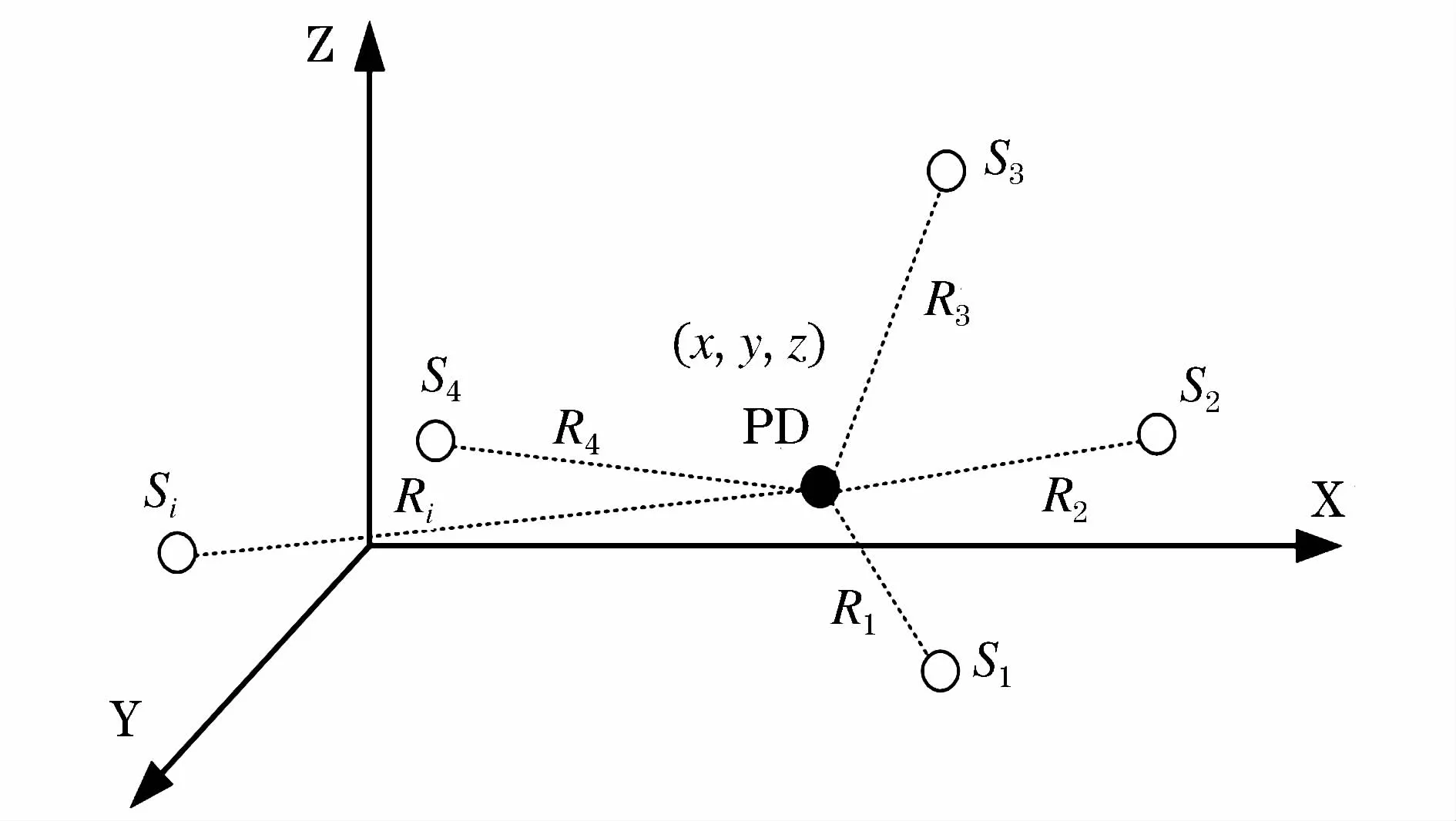
图3 局放源与传感器位置示意图Fig.3 Schematic diagram of PD source and sensors location

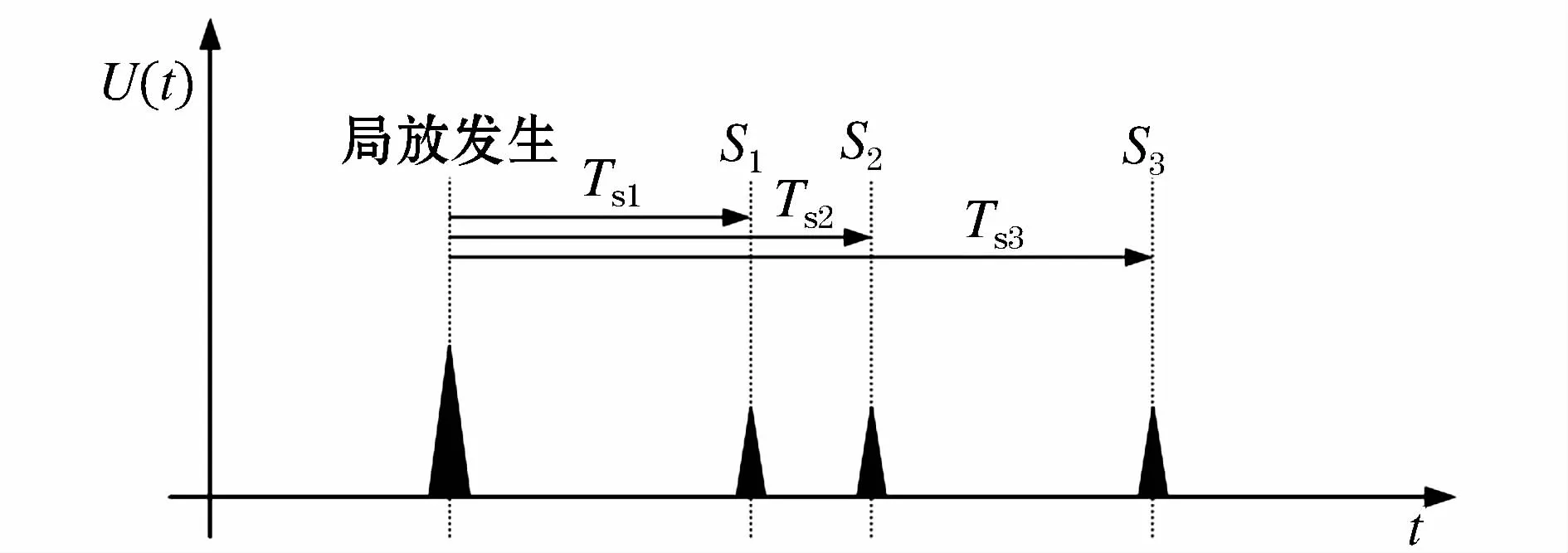
图4 绝对时间法传感器测量时间示意图Fig.4 Schematic visualization diagram of arrival timeswith absolute timemethod interference known PD onset

假设局放源的空间坐标为（x，y，z），传感器的信号采集时间为Tsi，电磁波信号传播速度为vs，三个坐标（xsi，ysi，zsi）已知的传感器，根据球面公式可以得到：

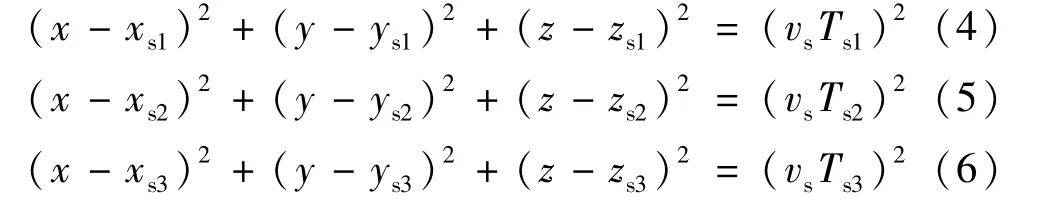
其中每个球面的半径为：

运用绝对时间法在实际的局放检测工作过程中局放的发生是随机的，即三个传感器的信号起始时刻Tsi并不能精确获得的。这会使得局放的检测和定位发生误差而严重影响定位的精准性。

2.2 时差法

鉴于绝对时间法的严重缺陷，文献［7，18］提出采用时差法进行求解，将传感器的配置数增至4个。时差法的思想为设定某个传感器最先采集到信号的同时触发其他的传感器进行录音，运用4个传感器可以建立三个非线性方程进行求解。如图5所示，从第一个采集到信号开始触发其他的传感器录音可以得到三个时差τ1i，建立的球面非线性方程中增加了未

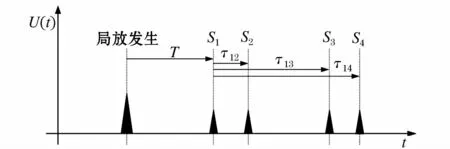
图5 时差法传感器测量时间示意图Fig.5 Schematic visualization diagram of signal time differencesmethod by the unknown T

知时间T和不同的时差τ1i，而未知数仍为局放源坐标（x，y，z），如方程（8）～方程（10）：

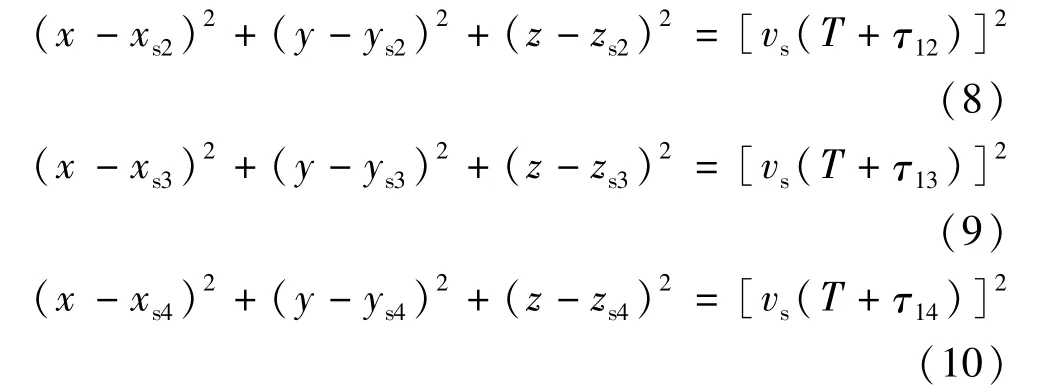
可经过迭代求解，得到的非线性方程组的解即为局放源的坐标。

2.3 静态伪距方程代数求解法

静态伪距方程代数解法是针对“GPS模型”所获得的非线性定位公式的代数直接求解方法［20］，伪距观测方程为：

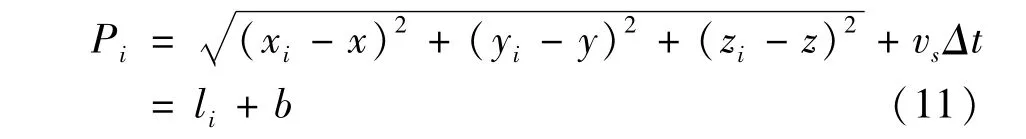
式中 （x，y，z）是待求解观测点坐标；（xi，yi，zi）是第 i个 GPS的卫星位置坐标，i=1，2，…，n。li=是第i个卫星到待测点的几何距离，b表示接收机钟与卫星钟之间相对钟差的几何等效距离。根据方程（11）可得：

令 di，i+1=Pi-Pi+1，可得：由式（13）平方移项可得：

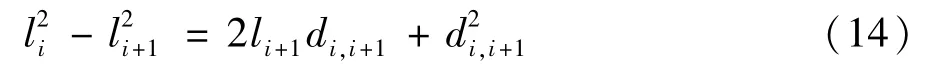
而由于平方项：

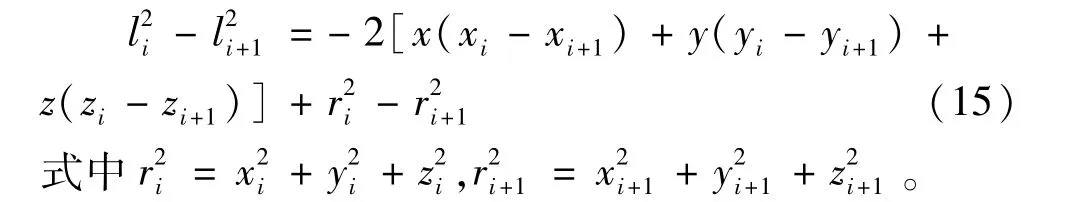
式（14）、式（15）相等，可得：由式（16）、式（17）相等可得：

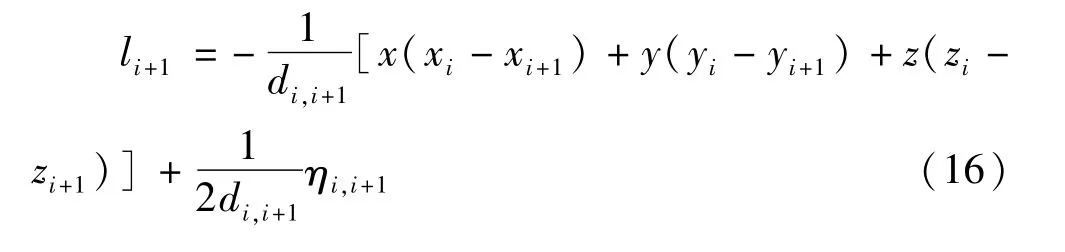
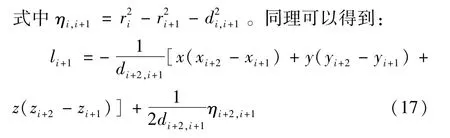
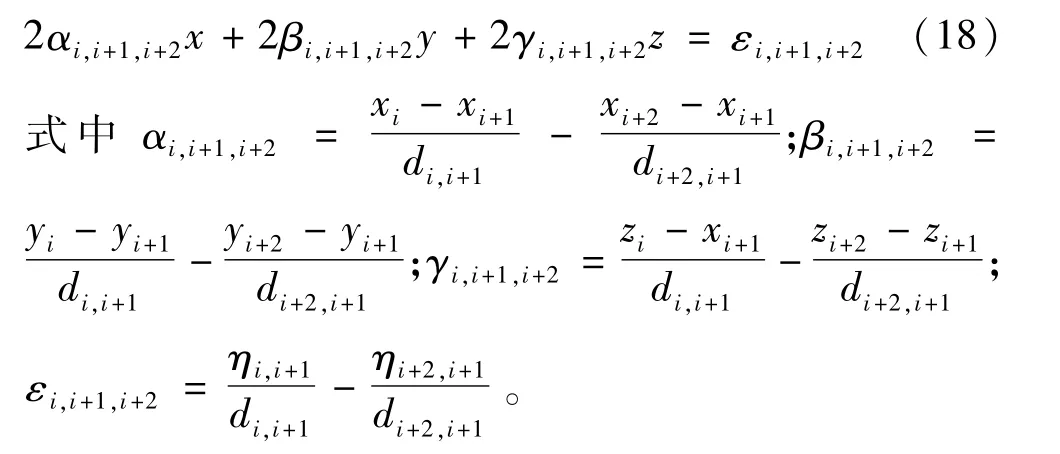
可见，通过3个伪距测量方程可以形成式（18）的线性方程。将此方法引入局放定位中，可以通过建立关于未知数（x，y，z）的线性方程组，以代数法求解得到局放源的坐标［21-22］。

2.4 伪信号起始时刻法与伪距代数求解法的结合

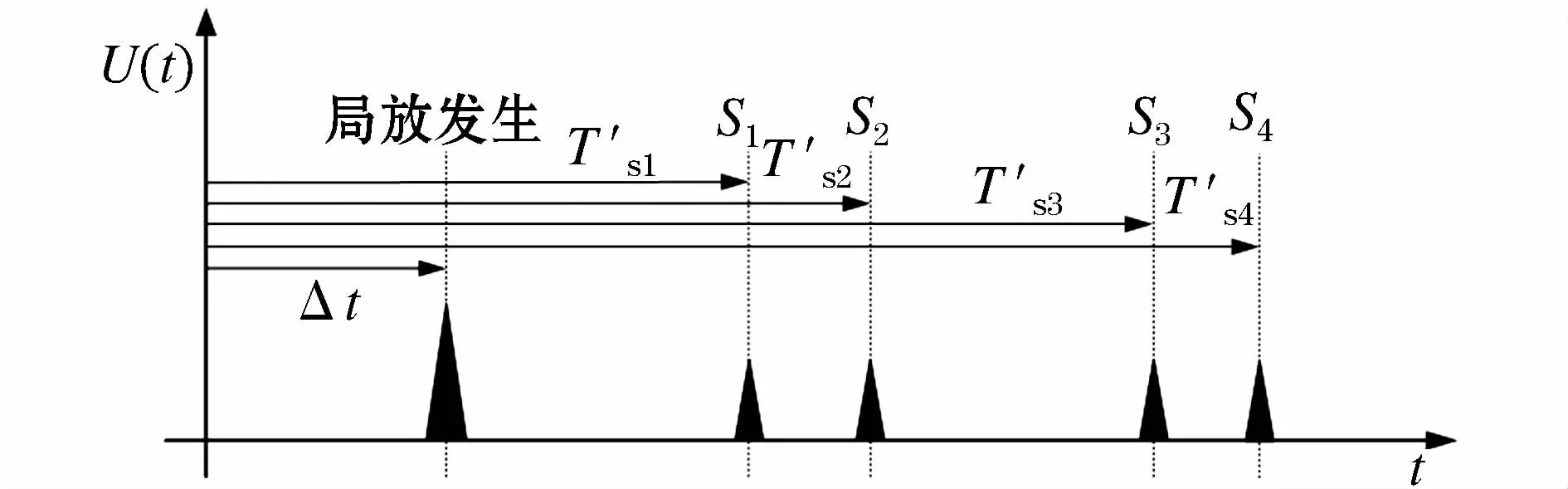
图6 伪信号起始时刻法传感器测量时间示意图Fig.6 Schematic visualization diagram of pseudo-times in reference to the unknown PD onset t

如图6所示，伪信号起始时刻法可同样采用4个传感器接收局放辐射的UHF信号，在某一时刻（起始时刻，超前局放发生时刻的时间为Δt）同时录音，传感器接收到信号的时刻为T′si。由于信号起始时刻T′si中包含了未知的采集时间偏移量Δt，所以称其为“伪信号起始时刻”，局放源坐标与传感器坐标可得到如下方程［19］：

仿照伪距方程法可得到：

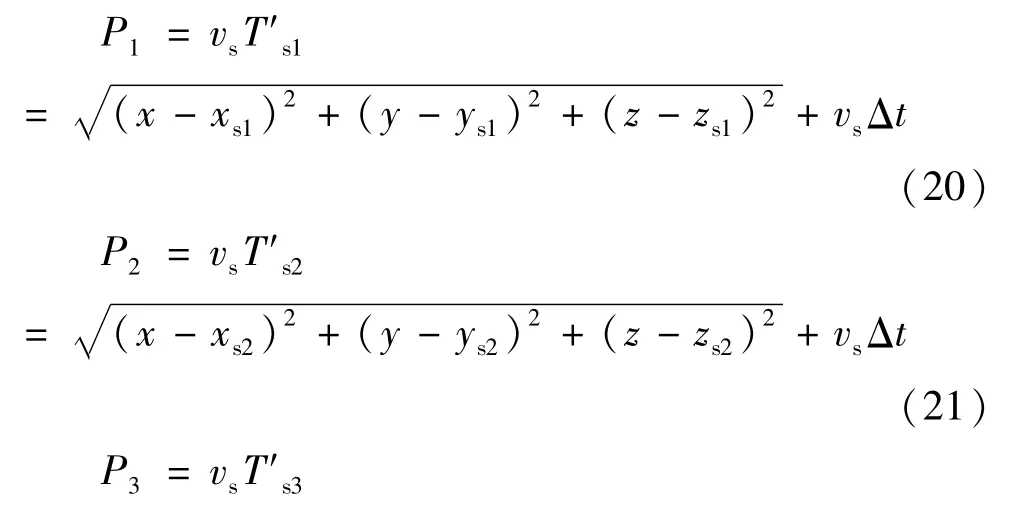
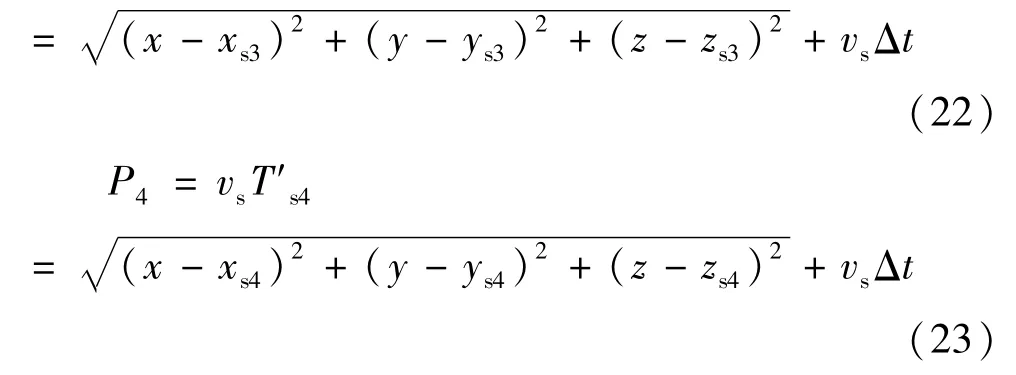
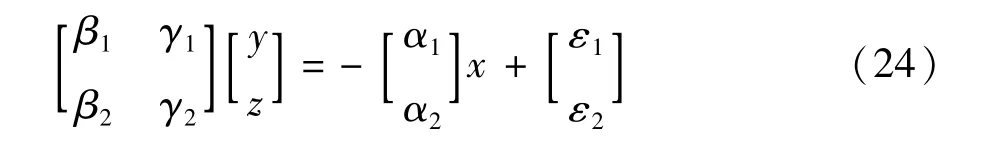
又由于：

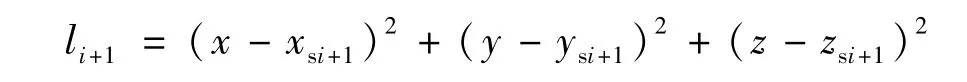
得到：

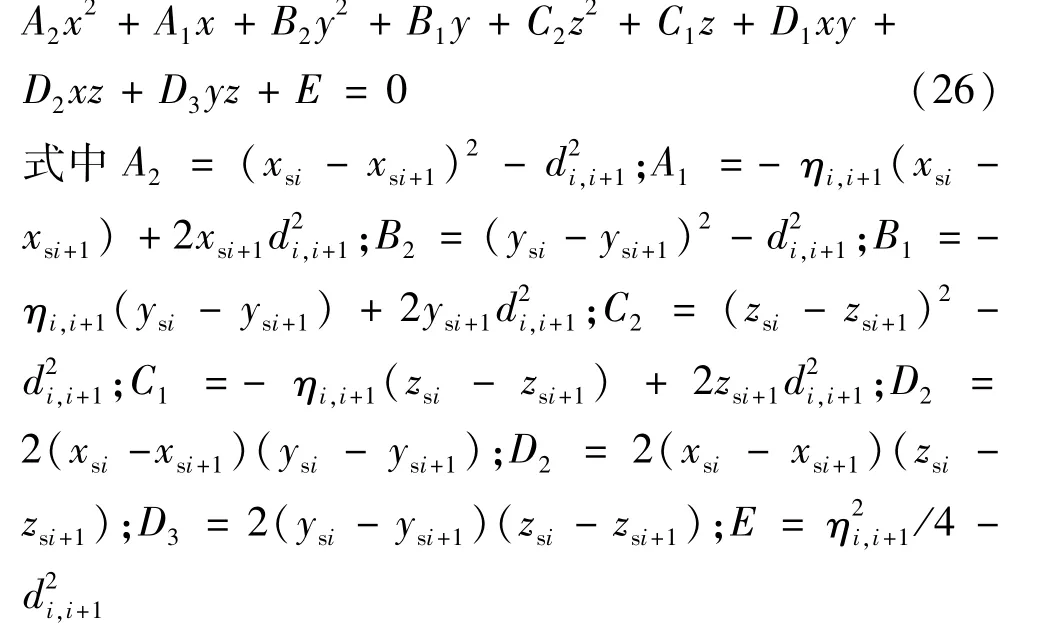
独立参数的解可以通过将方程（25）带入方程（26）形成一个关于独立状态参数的一元二次方程，这个一元二次方程可以写为：

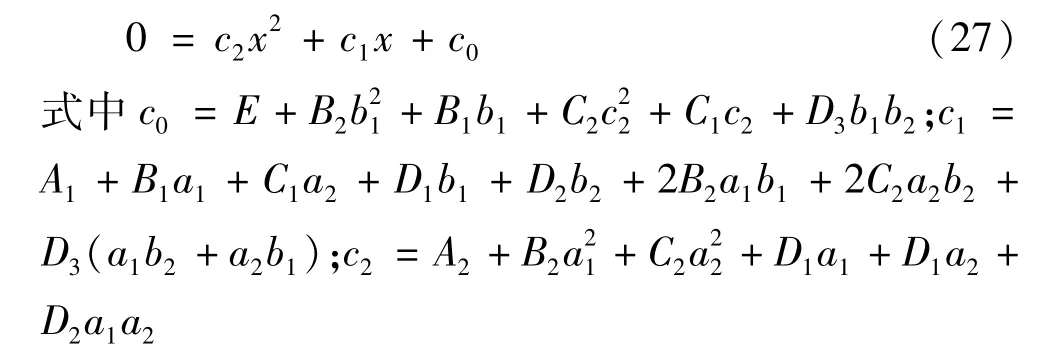
把方程（27）的每一个解带入方程（25），则可得到非独立状态变量相对应的值。如果方程（27）的两个值分别定义为x（+）和 x（-），则可得到两组结果：（xA，yA，zA）和（xB，yB，zB），这两组值中只有一个满足方程（20）～方程（23），其值就是局放源的坐标。方程（27）的解表示如下：

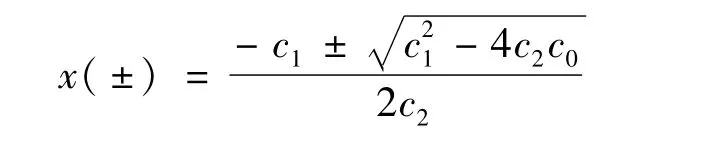
通过分析可知，利用绝对时间法、时差法或“伪信号起始时刻法”可以建立局放源与传感器空间坐标的非线性方程组，一般可采用迭代算法求解，而迭代算法最明显的缺点是求解的精度对初值的选取有很强的依赖性。相反，将“伪信号起始时刻法”与静态伪距方程代数解法结合，可以通过代数运算直接求解非线性方程组，并且在不可避免的测量错误、灵敏度限制等情况下，直接运算求解的方法更精确、更稳定。

3 现场局放定位

3.1 现场布置

为验证上述局部放电源的定位方法在现场受到干扰时的合理性和有效性，在变电站进行现场测试。将传感器布置于变电站现场，4个传感器的坐标分别为：S1（0，5，0）、S2（10，5，0）、S3（10，0，0）和 S4（0，0，1），单位为m，如图7所示。

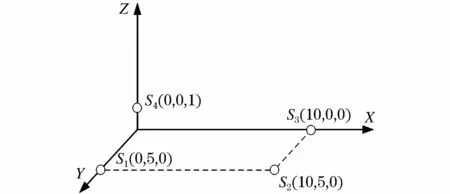
图7 传感器现场布置坐标Fig.7 Coordinate of sensors onsite location

3.2 实地测量

现场测量的结果见表1，将模拟放电源先后布置于、及三个不同的位置时，测量结果见表格1，其中定位误差为几何距离误差。

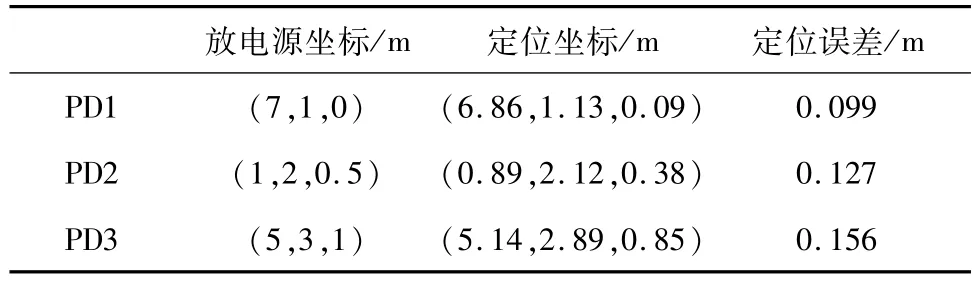
表1 现场测量结果Tab.1 On-site test results

由表1可知，采用静态伪距方程代数求解法求解依据伪信号起始时刻法建立起的非线性方程组时，计算结果具有很高的精度，应用于局放源空间定位中是合理的。

4 结束语

局放测量作为诊断工具越来越多的应用于电力设备工作状况判断以及设备绝缘系统老化问题的评估。对设备的绝缘系统状态的持续评估和诊断既有助于整个系统的连续性风险评估，也利于绝缘故障的早期发现。

文章以局部放电时辐射产生的超高频电磁波信号（UHF信号）为检测对象，利用改进的能量积累函数确定信号的起始时刻，避免了传感器接收到现场的各种噪声而误判UHF信号的起始时刻；以伪信号起始时刻法建立局放源坐标与传感器坐标的非线性方程组，用静态伪距方程代数求解法直接求解非线性方程组，保证了求解的速度和精度，避免了迭代算法的求解精度对初值选取的依赖性。