探索求不等式的解与求方程的根解法的联系

无锡技师学院（江苏省无锡立信中等专业学校） 佘加平

探索求不等式的解与求方程的根解法的联系

无锡技师学院（江苏省无锡立信中等专业学校） 佘加平

不等式是初等数学中比较重要的部分，在学习函数之前，学习一元二次不等式的解法，特别是将一元二次不等式的解与相应的一元二次方程的解联系起来，有助于学生对相关知识的理解和掌握。但是，对于中职学校的学生来说，解不等式有些困难。按照中高职教学要求，以能力为本位，够用为目的，并培养学生的基本运算能力、基本计算使用能力和简单实际应用能力，我对解不等式的方法与初中课程中解方程的根的方法进行比较、归纳和总结，让学生在较短的时间内熟练掌握解不等式的方法。

方程；一元二次不等式；绝对值不等式；分式不等式

以下我将从一元二次不等式、绝对值不等式、分式不等式的解与方程根的解法做个比较。

一、一元二次不等式

1.转正，即把二次项系数转化为正数，下面提到的方程或不等式都是a＞0的情况；

2.求根，运用初中所学的“直接开平方法、配方法、公式法、因式分解法、十字相乘法”解一元二次方程，得到两个根x1，x2（x1＜x2）；

3.放x，这一步很关键。第一，我们把小根x1写在左边，大根x2写在右边，即x1x2；第二，看看不等式在a＞0时不等号的方向，运用“小于号，x放中间，大于号，x放两边”，即x1xx2，（或者xx1x2x）；第三，用“＜”连接，即x1＜x＜x2，（或者在x＜x1x2＜x中间填“或”得：x＜x1或x2＜x），因此就得到了的解。

二、分式不等式

1.首先，我们把等式转化为不等号的右边是0，左边是分式的形式；

2.然后把x前面的系数转化为正，也就是我们讨论a＞0和c＞0的情况；

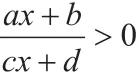
三、绝对值不等式

1.首先我们得把x前面的系数转化为正，即a＞0；

3.我们把小根x1写在左边，大根x2写在右边，即：x1x2，然后我们看看绝对不等式不等号的方向，运用“小于放中间，大于放两边”，即x1xx2，（或者xx1x2x），然后用“小于号”连接，即x1＜x＜x2，（或者x＜x1x2＜x中间填“或”得：x＜x1或x2＜x），由此得到绝对值不等式的解。

根据以上三种不等式的求解过程可以看出，对于“有根”的情况，我们可以用一种方法套用，即先解关于其的“方程”，求出相应的根，再用“小左大右”及“‘小于’x放中间，‘大于’x放两边”的原则，最后用“小于号（或小于等于号）”连接就解出了不等式的解集。这样的方法简单，方便，容易记忆，对于中下层的学生来说很容易把握解不等式的问题，但是此“套用方法”对于比较复杂的绝对值不等式和分式不等式并不适用。这是我在教学的过程中摸索出来的求不等式简捷方法，在具体的运用中收到了很好的效果，以此论文供大家探讨。

[1]杨裕前、董林伟.数学九年级上册[Z].义务教育教科书.江苏教育出版社，2014年12月第3版：9-11.

[2]马复、王巧林.数学第一册[Z].江苏省职业学校文化课教材配套教学用书.江苏教育出版社，2011年8月第1版：43-50.