《函数的单调性》说课稿

甘肃省甘南州合作第一中学 冯 菀

《函数的单调性》说课稿

甘肃省甘南州合作第一中学 冯 菀

尊敬的各位老师：

大家好！

今天我说课的题目是《函数的单调性》，它是高中数学人教A版必修一第一章第3节“函数的单调性与最值”的第一课时。

一、教材分析

1.教材的地位和作用

单调性是函数的第一个重要性质，从知识结构上看，它既是函数概念的延伸和扩展，又为后续研究指数函数、对数函数、幂函数的单调性奠定了基础，对进一步探索、研究函数的其他性质有着示范作用，它在整个高中数学知识中起着承上启下的作用。

2.教材内容

函数的单调性主要学习函数单调性的定义和用定义证明函数的单调性。

3.教材的重难点

根据新课标要求和教材分析，本节课的重点是函数单调性的概念，判断并证明函数的单调性；难点是引导学生归纳出函数单调性的定义以及根据定义证明函数的单调性。

二、学情分析

1.有利因素：在初中阶段，学生对函数的单调性已经有了“形”的直观认识，知道用“y随x的增大而增大或减小”描述图像的“上升”或“下降”，具备一定的观察、类比、分析、归纳的学习能力。

2.不利因素：甘肃甘南是民族地区，绝大多数学生是民族生，根据民族生的特点，识记是强项，但逻辑思维水平不高，抽象概括能力不强，推理论证能力也比较薄弱，还需要在单调性定义的形成和用定义证明函数的单调性的过程中进一步培养和加强。

三、教学目标

根据上述教材和学情分析，结合新课标和教学大纲以及学生的认知水平，制定出以下三维目标：

知识与技能：

1.理解函数单调性的概念。

2.会根据函数的图像判断函数的单调性。

3.能根据单调性的定义证明函数的单调性。

过程与方法：

1.培养学生利用数学语言对函数单调性的概念进行概括的能力。

2.利用函数图像判断函数的单调性，使学生领会数形结合的数学方法。

3.通过用定义法证明函数的单调性，进一步加强学生的逻辑推理能力。

情感态度与价值观：

1.通过学生熟悉的生活背景导入，激发学生学习数学的兴趣。

2.通过问题串的引入，使学生积极参与教学活动，获得成功的体验，增强学生学习数学的信心。

四、教学模式

为了提高课堂效率，达到预定目标，结合本节课的知识特点，我的教学模式定为“六步导入法”：

1.情境导入，观察分析；2.新课探究，发展思维；

3.小组合作，展示点评；4.梳理精讲，强化应用；

5.巩固反馈，随堂训练；6.归纳小结，分层作业。

五、教学方法

根据本节课的教学内容和教学重难点，在教法上，我采用从抽象到具体，从特殊到一般的方法形成增函数的定义，再引导学生通过类比归纳的方法形成减函数的定义，在例2的证明中采用分析板演法来培养学生的逻辑推理能力。

在学法上，学生利用数形结合的思想对函数的单调性有了感性的认识，通过小组合作探究的方式充分调动学生的积极性和主动性，类比出减函数的定义，通过巩固训练环节加强基础知识，实现教学目标。

六、教学过程

（一）新课探究

1.增函数定义的形成（增函数的定义见PPT）：

学生：拿出事先准备的坐标纸，在坐标纸上画出一次函数y=x和二次函数的图像。

问题1：通过观察一次函数和二次函数的图像，描述随着自变量的增大，图像是怎样升降的？

方案1：在区间上取自变量1，2，因为1＜2，f（1）＜f（2），所以f（x）在（0，+∞）上的图像逐渐上升。

方案2：在（0，+∞）上取无数组自变量，验证随着x的增大，f（x）也增大。

方案3：举反例，若在区间上取自变量3，4，3＜4，f（3）＞f（4）显然不成立。

方案4：在（0，+∞）内取任意的x1，x2且x1＜x2时，都有f（x1）＜f（x2）成立。

【设计意图】在这一环节中，考虑到学生会对增函数定义的形成有困难，主要采取以下方法：

1.回答情景导入中的问题2，从直观上认识增函数。

2.通过4个方案，用从抽象到具体，特殊到一般的方法刻画函数单调性定义形成的过程，突出重点，突破难点。

（二）小组合作

1.减函数定义的形成（减函数的定义见PPT）：

从函数y=x2的图像上可以看到，图像在y轴左侧是下降的，那么：

（1）图像下降，自变量与因变量之间有什么关系？

（2）如何用数学语言来描述这种“下降”呢？

【设计意图】在这一环节中，类比增函数的定义，让学生通过小组讨论概括出减函数的定义。

（三）梳理精讲—应用

在理解概念的基础上，让学生总结判别函数单调性的方法，并进行简单的应用。

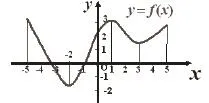
例1 下图是定义在[－5，5]上的函数y＝f（x）的图像，根据图像说出函数y＝f（x）的单调区间，以及在每一单调区间上，y＝f（x）是增函数还是减函数。

归纳：本例中解决的易错点：

（1）单调区间一般不能合并；

（2）当端点满足单调性定义时，可开可闭。

【设计意图】例1的解决让学生学会通过函数图像来判断函数的单调区间及在各区间的单调性。

根据学情分析，在处理例2时，考虑到学生对作差后的变形和对因式符号的判断有一定的难度，因此教学中，我采取一边分析，一边板演证明过程的方法来解决这一难题，然后提炼基本步骤，强化变形的方向和符号判定方法，接着让学生板演实践。

归纳：定义法证明函数单调性的步骤：

五步：取值--作差--变形--定号--下结论。

【设计意图】通过解决例2弥补学情中的不足，提高学生的逻辑推理能力，通过实践规范学生的证明步骤。

【备注：此说课稿在全国第四届和谐杯说课大赛中获一等奖】