黏弹性阻尼材料对整体叶盘固有特性的影响

王 娇，于 涛，张曰浩

(烟台大学 a. 机电汽车工程学院；b. 山东省高校先进制造与控制技术重点实验室；c. 工程实训中心, 山东 烟台 264005)

黏弹性阻尼材料对整体叶盘固有特性的影响

王 娇a, b，于 涛a, b，张曰浩c

(烟台大学 a. 机电汽车工程学院；b. 山东省高校先进制造与控制技术重点实验室；c. 工程实训中心, 山东 烟台 264005)

整体叶盘是航空发动机的关键部件，在多场耦合复杂边界条件作用下，容易发生复杂的振动，当叶片发生疲劳破坏时，导致整体叶盘的叶片无法更换.为提高整体叶盘的抗高周疲劳能力，提出在整体叶盘盘缘底部添加黏弹性阻尼材料以实现整体叶盘振动抑制的方法，采用复常量模型表征添加在整体叶盘盘缘的黏弹性阻尼材料，基于模态应变能法计算整体叶盘复合结构的固有频率和损耗因子，对比涂层厚度对整体叶盘固有特性的影响.结果表明，随着涂层厚度的增加，整体叶盘的低频固有频率增加，高频振动频率降低，损耗因子增大，振型变化较小.

整体叶盘；黏弹性阻尼；固有频率；振型；损耗因子

整体叶盘是轮盘和叶片加工成一体，形成一整体结构，省去了叶片的榫头和轮盘的榫槽，具有减重、减级、增效和强可靠性等优点[1 - 3].但是，由于航空发动机处在高温、高压、高转速的恶劣工况下必然产生整体叶盘的振动问题.据统计资料[4]表明，因整体叶盘失谐振动而导致的盘片高周疲劳故障占发动机总故障的25%，如此高的故障率严重影响了发动机的经济性、可靠性和安全性.为此，采用黏弹性阻尼以实现整体叶盘的减振，提高其抗振动疲劳能力，对提高航空发动机整体叶盘的性能具有重要价值[5].

国内外抑制整体叶盘振动的方法通常是在轮盘或叶根处增加阻尼结构，达到抑制整体叶盘振动和避免整体叶盘振动损伤的目的.整体叶盘减振的主要形式有叶根缘板阻尼[6 - 8]、轮盘上添加压电材料、利用压电分流阻尼降低盘片振动[9].近年来，国际上出现了新的整体叶盘阻尼减振措施， 即将黏弹性材料施加在轮盘上实现有效减振，其已经在工程中得到了初步的应用[10]， 但是，相应的研究较少.本文采用有限元法，对整体叶盘复合结构进行模态分析，研究黏弹性材料阻尼对整体叶盘固有特性的影响.

1 带有黏弹性阻尼的整体叶盘的有限 元建模

使用Pro/E创建整体叶盘的三维实体模型，由于航空发动机整体叶盘为循环对称结构，建模时只需建立整体叶盘的1/24，即一个基本扇区，如图1(a)所示，然后通过循环对称得到整体叶盘结构[11]，如图1(b)所示.采用有限元软件ANSYS对带有黏弹性阻尼材料的整体叶盘进行模态分析，其中，有限元模型的单元类型选择Solid 185单元，采用自由网格进行网格划分，并采用voffst命令形成黏弹性涂层，使两个实体接触面的节点有效地耦合，涂层位置如图1(a)所示.整体叶盘的材料为钛合金Ti-6Al-4V，其弹性模量为110 GPa，泊松比为0.3，密度为4 500 kg/m3. 黏弹性阻尼涂层材料为Zn-33，其弹性模量为1 GPa，泊松比为0.498，密度为930 kg/m3，损耗因子为0.968 3.整体叶盘的有限元模型共有11 328个节点和49 842个单元，其中，黏弹性阻尼块共有2 947个节点和1 098个单元.模态分析的边界条件为约束轮盘与转轴连接的部位，如图1(b)所示.模态求解方法采用Block Lanczos模态提取法，并采用模态应变能法获得带有黏弹性阻尼材料的损耗因子.

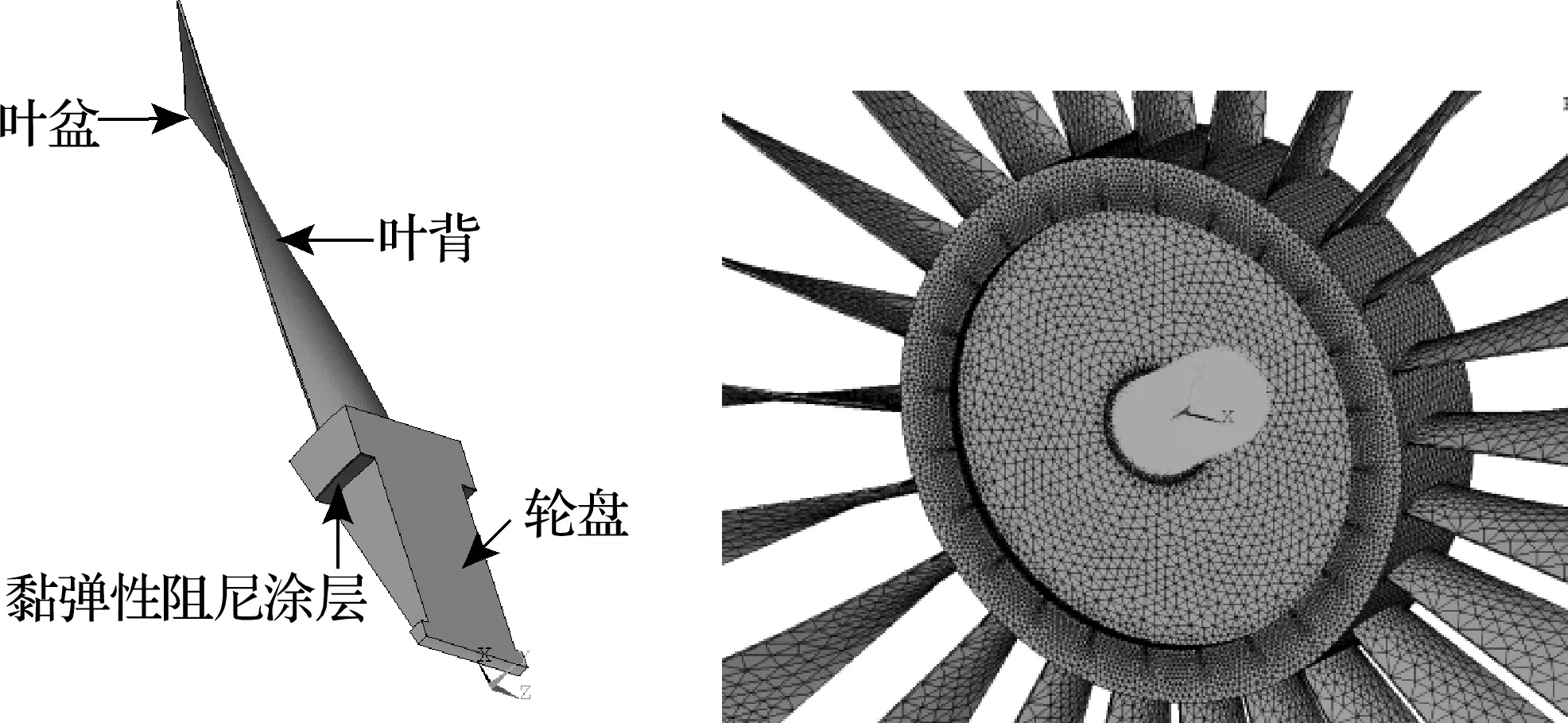
(a) 实体模型 (b) 有限元模型图1 带有黏弹性阻尼的整体叶盘模型Fig.1 Blisk model with viscoelastic materials

2 黏弹性阻尼涂层厚度对整体叶盘固 有特性的影响

2.1 固有频率分析

采用ANSYS软件分别对整体叶盘和带有黏弹性阻尼材料的整体叶盘进行模态分析，获得相应的固有频率和振型. 表1为整体叶盘的0～5节径的固有频率的计算结果. 为了与未带有黏弹性阻尼涂层的整体叶盘进行对比分析，在轮盘盘缘上添加涂层厚度分别为20 μm和1 mm的黏弹性材料，固有频率计算结果如表2所示. 表3给出了添加不同涂层厚度的整体叶盘0节径下21～30阶的固有频率.

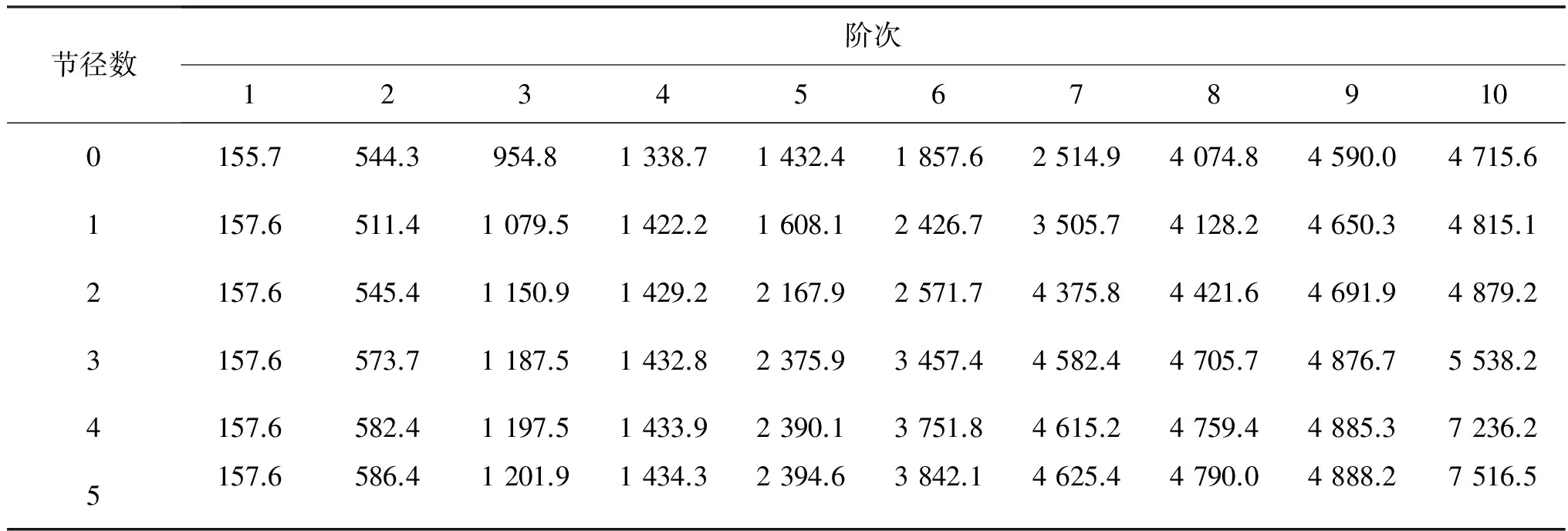
表1 整体叶盘0～5节径的固有频率

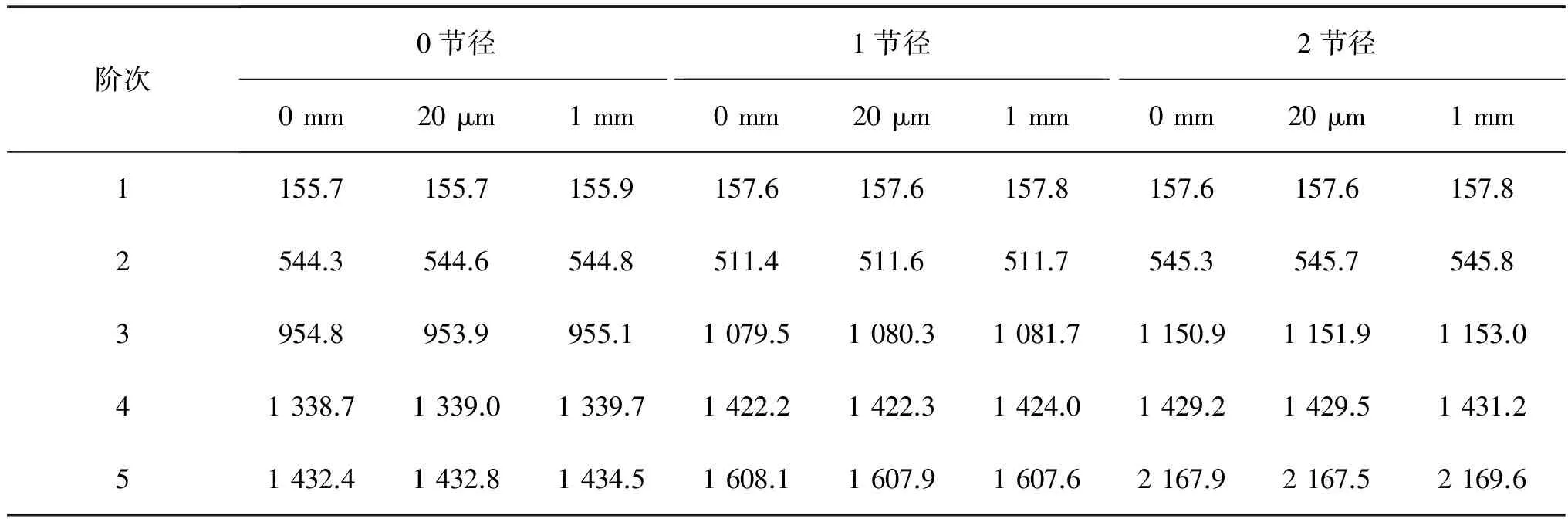
表2 不同涂层厚度下整体叶盘的固有频率

表3 不同涂层厚度下整体叶盘的高阶固有频率

由表1可知，整体叶盘由于结构的对称性，在非0节径时，相邻两阶的振动频率相同，因此，表1给出了在非零节径的前20阶固有频率中的10阶.整体叶盘耦合振动随着节径数的增多，相应的固有频率基本上随之增高，耦合振动固有频率将趋近叶片一阶“轴向”弯曲振动频率，轮盘将不再振动.

由表2和3可知，在轮盘轮缘处添加黏弹性阻尼材料后，整体叶盘的固有频率发生了改变，随着涂层厚度的增加，低频振动呈现固有频率增大的趋势，在超过20阶后多数呈现固有频率降低的趋势.

不同涂层厚度在不同阶次下整体叶盘的损耗因子如表4所示.由表4可知，在轮盘轮缘处添加黏弹性阻尼材料后，损耗因子随着涂层厚度的增加而增加.

表4 不同涂层厚度下整体叶盘的损耗因子

2.2 振型分析

由于整体叶盘将叶片和轮盘进行刚性连接，因而其振型具有叶片和轮盘两者的特点，主要有节圆振动、节径振动以及具有节圆和节径的复合振动.

(1) 节圆振动. 整体叶盘振动时，轮盘在节圆上各点静止不动；在同一半径圆上各质点振动幅值和相位相同；在节圆内外两侧各质点作相位相反的振动[12].表5为整体叶盘有无黏弹性阻尼涂层的节圆振型图.由表5可知，在整体叶盘上添加黏弹性材料对振型的影响不大.随着振动频率的增大，整体叶盘振动的最大振幅多数出现在叶片的叶尖处，只有在整体盘片振动频率达到15 554.6 Hz时，振动幅值最大值同时出现在轮盘和叶片的叶尖处，并出现了轮盘转动的现象.节圆振动只有在整体叶盘的刚性不足的情况下才能够发生.对于具有节圆振动的轮盘，节圆有时会跑到轮盘外，而存在于叶片处，特别像航空发动机中的风扇，具有较长叶片的轮盘极有可能产生这种情况, 如表5中整体盘片的第15， 16， 23阶对应的振型图所示.

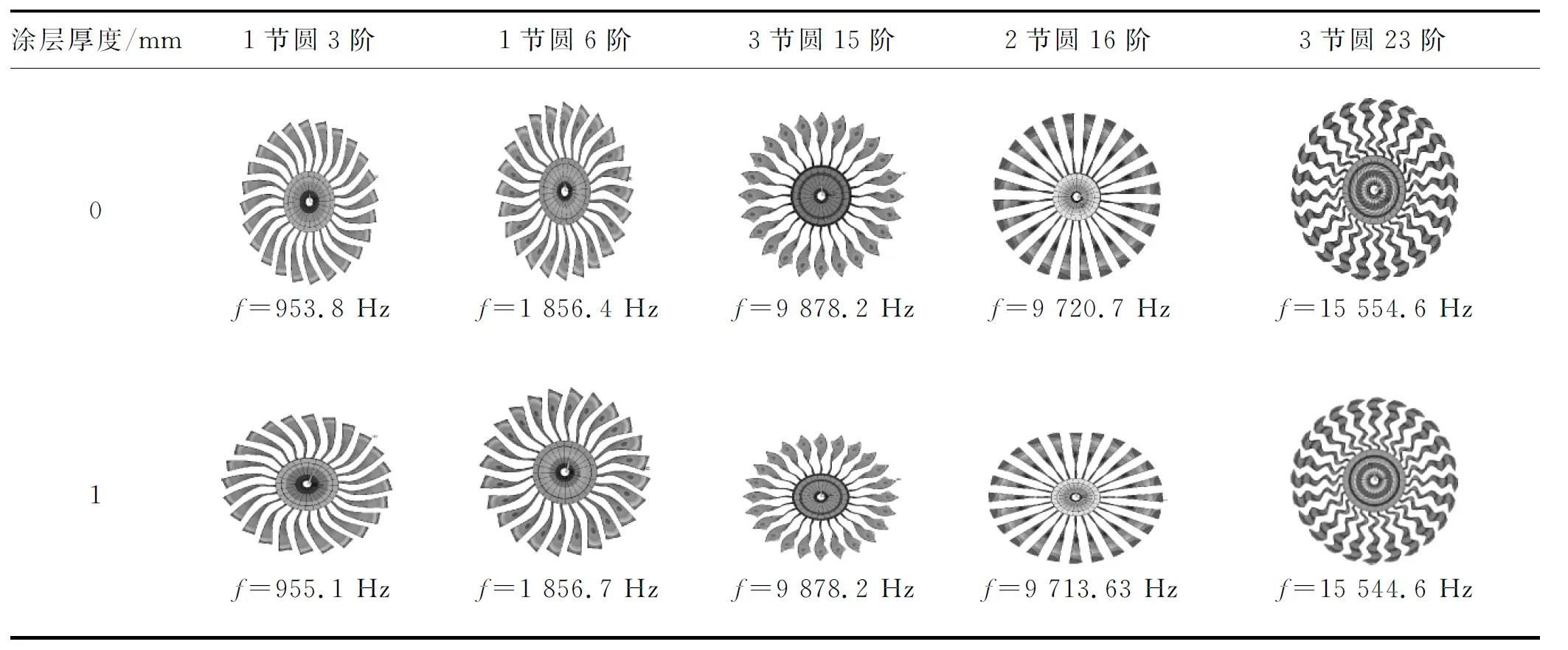
表5 整体叶盘有无黏弹性阻尼材料时的节圆振型图

(2) 节径振动. 轮盘出现沿直线方向分布不动节线的振动.表6为整体叶盘有无黏弹性阻尼涂层的节径振型图.由表6可知，当整体叶盘的振型中节径数为i时，24个叶片中就有2i个叶片不参与振动，以节径来分界，则相邻两节径之间呈现凹凸交替的若干扇形部分，节径两侧叶片振动方向是相反的，两个节径所夹扇形的中间位置叶片的振幅最大(称为波峰)，向两边到达节径处时叶片振幅最小(称为波谷)，剩下的一些叶片则以不同的振幅参与振动.低节径整体叶片的振动，危险性较大. 这主要是因为这种振型的频率较低，维持这种振动所需要的能量很小，容易引起整体叶盘的振动损坏，因此，对于低节径的整体叶盘振动应该予以重视.

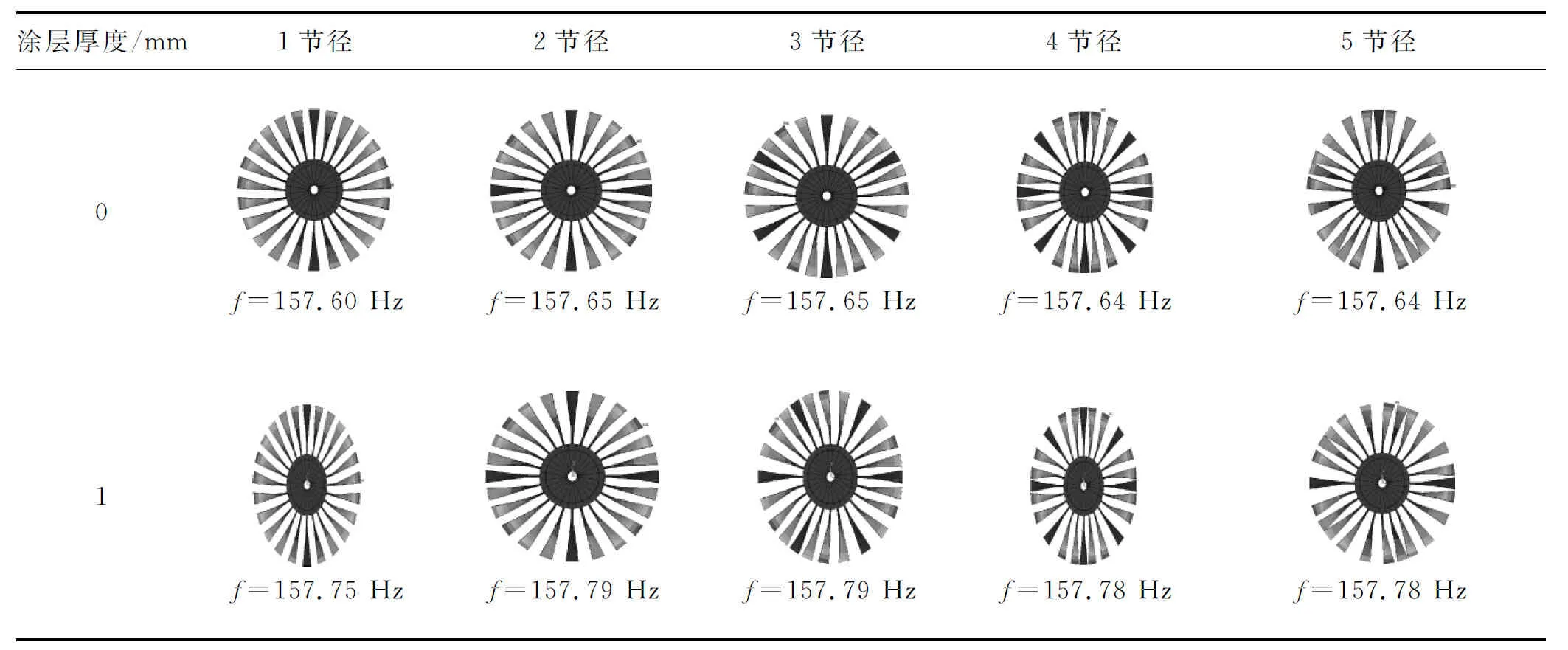
表6 整体叶盘有无黏弹性阻尼材料时的节径振型图

(3) 复合振动. 整体叶盘同时出现具有节径和节圆的振型.表7为整体叶盘有无黏弹性阻尼涂层的复合振动振型对比图.由表7可知，添加黏弹性材料后对整体叶片的振型影响较小.节径和节圆振动在试验和仿真中容易获得，频率较低，低频激振力可激起共振.复合振动由于频率高，需维持这种振动的能量大，实际中不容易产生.

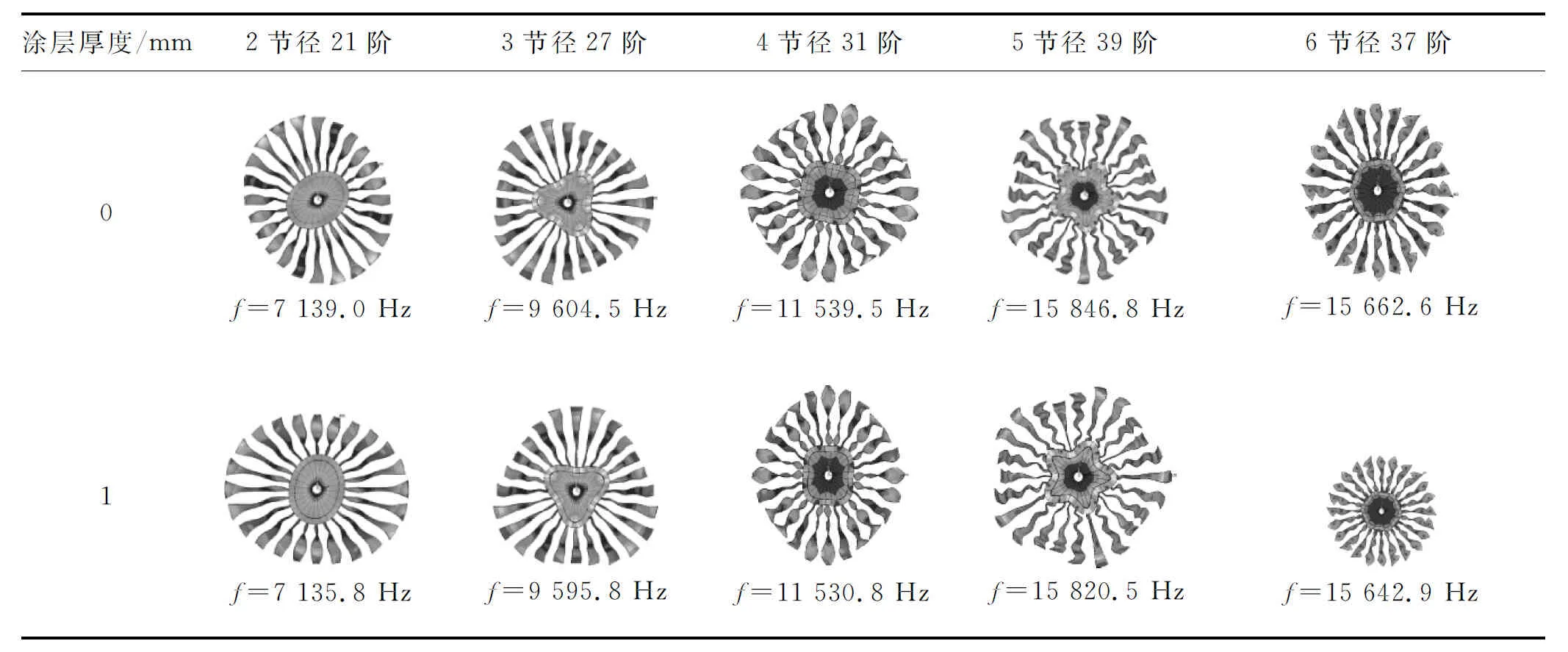
表7 整体叶盘有无黏弹性阻尼材料时的复合振动振型图

3 结 语

在整体叶盘盘缘上添加黏弹性阻尼材料，改变整体叶盘的固有频率和振型，采用模态应变能法获得整体叶盘的损耗因子.通过模态分析与对比，获得黏弹性阻尼涂层厚度的影响规律，结果如下所述.

(1) 在整体叶盘盘缘上添加黏弹性阻尼涂层后，整体叶盘的固有频率增大，振型变化不大. 涂层越厚则整体叶盘的低频振动固有频率越高，高频振动频率越低，损耗因子越大.

(2) 整体叶盘做节径振动时，对于同一节径，随着阶数的增大，整体叶盘的固有频率也在不断增大，节径数越多，相应的振动频率越高.随着激振力频率不断增加，最后轮盘将不再振动，而只有叶片的高阶振动.低节径整体叶盘振型频率较低，激起这种振动的能量较小，容易引起整体叶盘的振动损坏，危险性较大.

(3) 整体叶盘做节圆振动时，节圆有时会跑到轮盘外，而存在于叶片处，具有较长叶片的轮盘极有可能产生这种情况.

[1] 王增强. 航空发动机整体叶盘加工技术[J].航空制造技术，2013(9): 40-43.

[2] 黄春峰. 航空发动机整体叶盘结构及发展趋势[J].现代零部件，2005(4): 96-101.

[3] 吴大观. 航空涡喷、涡扇发动机结构设计准则(研究报告)[R].第三册-叶片.北京: 中航航空工业总公司发动机设计工程局, 1997: 26-27.

[4] 白斌，白广忱，童晓晨，等.整体叶盘结构失谐振动的国内外研究状况[J].航空动力学报，2014，29(1): 91-103.

[5] BALMES E, CORUS M, BAUMHAUER S, et al. Constrained viscoelastic damping, test/analysis correlation on an aircraft engine [M]// Structural Dynamics. New York: Springer, 2011: 1177-1185.

[6] YANG B D， MENQ C H. Characterization of contact kinematics and application to the design of wedge dampers in turbomachinery blading: Part 1-stick-slip contact kinematics [J]. ASME Journal of Engineering for Gas Turbine and Power, 1997, 120(2): 410-417.

[7] PETROV E P， EWINS D J. Advanced modeling of underplatform friction dampers analysis of bladed disk vibration [J]. Journal of Turbomachinery, 2007, 129(1): 143-150.

[8] BERRUTI T. A test rig for the investigation of the dynamic response of a bladed disk with underplatform dampers [J].Mechanics Research Communications, 2010, 37(6): 581-583.

[9] ZHOU B，THOUVEREZ F，LENOIR D. Essentially nonlinear piezoelectric shunt circuits applied to mistuned bladed disks [J].Journal of Sound and Vibration, 2014, 333(9): 2520-2542.

[10] RAO M D. Recent applications of viscoelastic damping for noise control in automobiles and commercial air-planes [J].Journal of Sound and Vibration, 2003, 262(3): 457-474.

[11] 王娇，韩清凯，王相平，等.考虑振动-冲击-摩擦的旋转叶片动力学特性研究[J].数字制造科学，2012, 10(1): 43-52.

[12] 晏砺堂，朱梓根.结构系统动力特性分析[M].北京: 北京航空航天大学出版社, 1989: 78-79.

Effect of Viscoelastic Damping Materials on Natural Characteristics of Blisk

WANGJiaoa, b，YUTaoa, b，ZHANGYue-haoc

(a. School of Mechatronics and Automobile Engineering；b. Key Laboratory of Advanced Manufacturing and Control Technology in Universities of Shandong；c. Engineering Training Center, Yantai University, Yantai 264005, China)

As key components of air engine, blisk is exposed to complex vibration pattern. Blades of blisk often suffer from fatigue failure and can’t be replaced under multi-field coupling complex boundary conditions.In order to improve the anti-high-cycle fatigue of blisk, it is proposed here to introduce viscoelastic damping materials to suppress the blisk vibration. Using complex constant model to represent the constitutive law of viscoelastic material, the finite element model of blisk with viscoelastic material is established. Subsequently, modal strain energy method is adopted to calculate natural frequency, loss factor of blisk composite structure. Different coating thickness are compared to analyze the effects on natural characteristics of blisk. Results indicate that with the increase of coating thickness, low-frequencies increase, high-frequencies decrease, loss factors increase while modes show little variation.

blisk; viscoelastic damping; natural frequency; mode; loss factor

1671-0444 (2016)04-0554-05

2016-04-29

国家自然科学基金资助项目(11502227)；山东省自然科学基金资助项目(ZR2014EEP006)

王 娇(1985—),女，吉林辽源人，讲师，博士，研究方向为非线性振动、阻尼涂层减振等. E-mail: zoe_wangjiao@163.com

V 232.3

A