船舶运动状态下舵附推力鳍水动力性能分析

王文全王诗洋张天添

（1.中国船舶及海洋工程设计研究院 上海200011；2.大连职业技术学院 大连116035）

船舶运动状态下舵附推力鳍水动力性能分析

王文全1王诗洋1张天添2

（1.中国船舶及海洋工程设计研究院 上海200011；2.大连职业技术学院 大连116035）

采用基于RANSE的数值波浪水池技术和数值拖曳水池技术，针对75 000 t船模型开展带有纵摇和横摇运动的自航CFD模拟研究。首先进行静水中的船模阻力和自航CFD模拟，通过与模型试验结果比较，初步验证了文中的CFD模拟方法；随后开展不同运动状态下是否带有舵附推力鳍的船模自航CFD模拟，并对该种状态下的船模阻力、运动响应以及船后螺旋桨的推力和扭矩等进行分析，获得相关变化特性。该项研究对于运动中船舶快速性研究和预报等，具有较好的指导意义和参考价值。

舵附推力鳍；纵摇；横摇；自航

引 言

进入21世纪，能源问题已引起世界各国的高度重视，成为世界范围内的焦点问题之一，而节能减排俨然被视作经济发展中的一项紧迫任务。因此，研究船舶推进节能技术对于降低船舶能源消耗、节约船舶运输企业的燃油消耗费用，以及降低船舶对海洋环境的污染都具有重大的意义。

以往许多学者和研究人员对舵附推力鳍的节能效果分析均关注船舶在静水中的节能效果，而在进行数值计算时并未考虑船体在波浪中航行时的六个自由度的运动。静水工况的数值计算结果并不能反映实际船舶在海面航行时舵附推力鳍的节能效果［1-2］。

目前已发表的有关波浪中自航CFD模拟方面的文献主要来自于美国IOWA大学的Stern团队。Carrica等人开展了静水中带自由升沉、纵倾KCS船模自航以及顶浪中船模运动响应的CFD模拟［3］，计算分析了模型自航点下的船模升沉量、纵倾角和螺旋桨转速，以及规则波顶浪中船模的阻力和运动响应。

本文主要工作内容包括船-桨-舵系统在静水、迎浪和横浪状态下的水动力数值预报、计算，以及船-桨-舵-舵附推力鳍系统在静水及不同运动状态下的节能效果数值预报，这些问题均考虑流体的粘性及自由液面产生的影响［4］。文中，我们建立船体、桨、舵-舵附推力鳍系统模型，导入STAR CCM+软件中进行网格划分和数值计算，对船-桨-舵和船-桨-舵-舵附推力鳍系统进行计及自由液面的阻力、螺旋桨推力和螺旋桨转矩的数值计算；然后设置船体强迫纵摇与横摇模拟不同波浪参数，对船-桨-舵系统和船-桨-舵-舵附推力鳍系统进行不同运动状态下的阻力、螺旋桨推力和螺旋桨转矩的数值计算，对比其在静水中和不同运动状态下的推进节能效果，并加以分析。

1 数学模型

1.1 湍流模型

湍流模型可分为空间平均模型和时间平均模型。空间平均模型即大涡模拟，时间平均模型分为湍流粘性模型和应力模型。其中应力模型即雷诺应力模型（RSM），湍流粘性模型又分为线性湍流模型和非线性湍流模型［5］。考虑到船尾部桨后旋转尾流，本文采用雷诺应力方程湍流模型。

雷诺应力输运方程在直角坐标系下的表达式为：

该方程从左到右依次为：对流项、湍流扩散项、分子粘性扩散项、剪应力产生项、浮力产生项、压力应变项、粘性耗散项、系统旋转产生项。

雷诺应力方程模型可直接使用输运方程求解出雷诺应力，从而避免其他模型的粘性假设。可见，雷诺应力方程模型模拟强旋流较其他模型有明显优势［6］。

1.2 VOF方法

VOF方法是一种以计算流体占据网格单元体积份额的途径来捕捉自由液面的方法，由Hirt和Nichols［7］于20世纪80年代初提出。控制体中含有水和空气，空气的体积分数是αa，水的体积分数是αw，那么水的体积分数输运方程为：

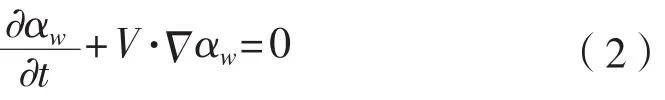
控制体中只充满水和空气这两种物质，所以水和空气的体积分数之和为1，即

采用VOF方法计算自由液面所需计算机的存储量小，有利于三维自由液面问题的模拟分析。其不足之处是不易获得准确的自由液面高度位置。

1.3 重叠网格方法

重叠网格方法（Overset grid）的最终目标是建立各重叠网格间的耦合关系，为各区域流场计算提供边界信息的传递服务。

如图1所示，网格1 落入网格2物面内的点被标记为洞内点而不参与流场的计算。网格1中与洞点相邻的点为洞边界点（图1中的方点），这些点通过插值接受网格2传递的流场信息。网格2的外边界点（图1中的圆点）也通过插值相应地接受网格1传递的流场信息， 任意变量f由相应的六面体贡献单元采用Trilinear 方法插值获得。网格1的洞边界点和网格2的外边界插值点之间的区域为重叠区域。

图1 重叠网格示意图

重叠网格将计算流域分成几个子域，各个子域的网格独立生成，并通过各域网格之间的嵌套、重叠等关系进行信息的传递，在重叠网格边界区域流场的信息通过插值进行耦合。重叠网格的生成主要包括两个方面：一方面，对背景域网格进行“挖洞”操作，即屏蔽洞面内部的区域，将洞面内网格进行标记并在CFD计算中予以舍弃；另一方面，洞边界之间的信息传递通过插值进行数值计算，即“寻点”问题。

2 计算模型的建立及网格划分

2.1 几何模型的建立

本文计算所选用的是75 000 t散货船，计算船模基本参数如表1所示。计算中使用的螺旋桨为自行设计的不等螺距螺旋桨（PBC1），螺旋桨模型的几何要素见表2。文中，舵附推力鳍的叶剖面类型为Clark-Y翼型，展长0.065 m、安装角度4°、弦长0.01 m，具体参数见表3。

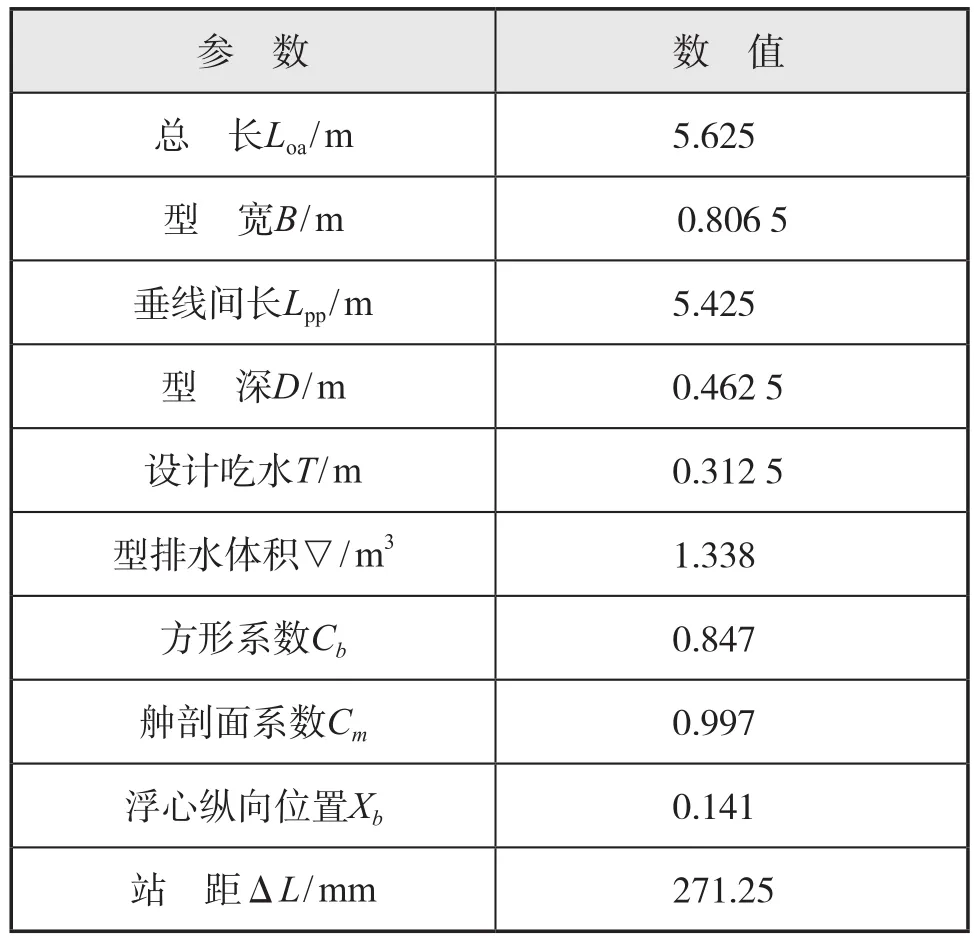
表1 船模基本参数

表2 原型桨（PBC1）的主要几何参数

表3 Clark-Y翼型型值表%

计算所用的船-桨-舵系统模型见图2。

图2 船-桨-舵系统模型

2.2 计算流域及网格的划分

本文采用重叠网格技术，将船体包含在一个小域中，然后再建立一个适当的背景域，将小域的边界与背景域的交界面生成Interface。该Interface边界条件类型设置成Overset Mesh Interface，使包含船体的小域按照设定的规则运动，同时在Interface的两个边界面上实现非定常流场的数值传递。计算船模自航时，还要在桨轴后给内外螺旋桨分别创建一个圆柱形小域。小域与桨毂同轴，其直径为螺旋桨直径的1.2倍，通过滑移网格方法模拟螺旋桨旋转运动。流体域、船体螺旋桨和开尔文波形区域具体如图3所示。

图3 网格划分

3 静水中的船-桨-舵系统水动力分析

3.1 静水中的裸船体阻力预报

分别计算船模在V=1.057 m/s、V=1.098 m/s、V=1.139 m/s，V=1.179 m/s、V=1.220 m/s、V=1.261 m/s、V=1.301 m/s以及V=1.342 m/s这八个速度下的阻力值，并同试验值进行对比分析。

表4为计算结果与试验值的比较。可见，船体阻力计算值与试验结果吻合较好， 最大相对偏差为2.6%，这说明本文所用方法可靠性佳。

表4 裸船体阻力值同试验值对比

3.2 静水中的船-桨-舵系统水动力分析

3.2.1 船桨舵系统水动力性能验证

以JBC（Japan Bulk Carrier）船模为计算对象，其中JBC船模被选为2015东京船舶水动力CFD Workshop（Tokyo 2015-A Workshop on CFD in Ship Hydrodynamics）的计算标模之一，其几何外形如图4所示。船模长7 m，螺旋桨模型直径0.203 m（实桨直径8.12 m）。AU型桨叶剖面的五叶桨几何外形如图5所示，主尺度参数见参考文献［8］。

图4 JBC船模外形

图5 螺旋桨外形

船模静水中自航CFD模拟中的网格划分及边界条件设置参照3.1节中船模静水阻力设置，得到CFD计算的静水中自航船模阻力、螺旋桨推力与转矩（见表5）。通过与试验值对比分析可以看出，CFD计算的船模阻力与模型试验结果非常接近，两者之间的差别在1%左右。螺旋桨推力、扭矩与模型试验结果也相当接近，差别在3%左右。

表5 船模静水中的自航CFD计算结果

通过对以上静水中船模阻力和自航CFD模拟结果的分析，初步证明本文的CFD计算方法能够进行船模静水状态下的自航模拟，且模拟结果具有相当高的精度。以上研究工作为后期开展相似船型船模静水及运动自航CFD模拟奠定了技术基础。

3.2.2 船桨舵系统水动力分析

通过生成网格并进行边界条件的设置，采用船速1.220 m/s、螺旋桨转速10.141 r/min（下面设置一致）。计算结果得到船-桨-舵系统水动力结果，见表6。

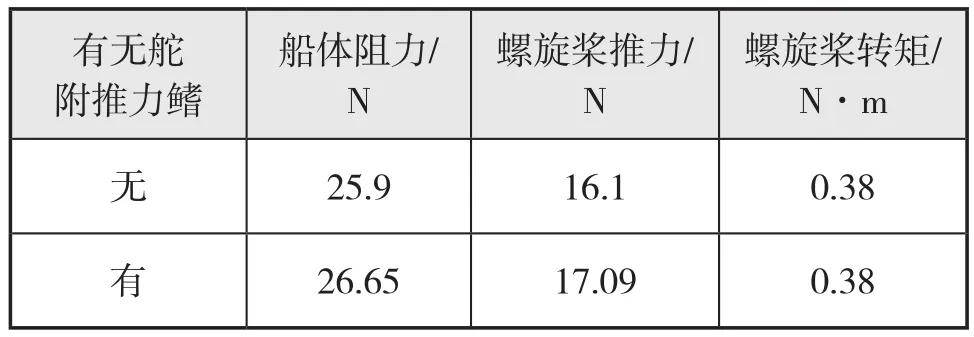
表6 船-桨-舵系统水动力数值计算结果（静水）

静水状态中，将船-桨-舵-舵附推力鳍系统的计算结果与船-桨-舵系统的计算结果比较后发现，前者船体阻力增加0.75 N、螺旋桨的推力增加了0.99 N，螺旋桨的转矩从数据上看没有变化。计算结果表明安装舵附推力鳍对螺旋桨的转矩没有明显的影响，船体阻力以及螺旋桨推力均有所增加。

图6为船体表面的自由液面的计算结果图形，红色部分和蓝色部分的交界处为自由液面，图7为开尔文波形图。舵附推力鳍对于船体自由液面的分布没有明显效果。从自由液面位置图可以明显看出在船体首柱位置自由液面明显升高，船首处波面升高最大是由于船首处为船体周围流线的驻点所在的位置，流体压力最大。为平衡这一压力升高，流体液面升高，以平衡此处的压力变化。液面升高后又逐渐下降然后再升高，从船体中部往后，液面升高渐趋不明显。

图6 船体表面自由液面

从图8的十字型参考线明显可见船-桨-舵-舵附推力鳍系统的桨后盘面处的速度分布更接近左右对称，而船-桨-舵系统的桨后盘面处的速度分布则逆时针旋转一定角度，表明船-桨-舵系统的桨后尾流的旋转比船-桨-舵-舵附推力鳍系统更为强烈，从而浪费螺旋桨输出能量［9-14］。

图7 开尔文波形图

图8 螺旋桨后盘面处速度分布云图

4 运动中的船-桨-舵系统水动力分析

船舶运动通过重叠网格技术来实现，通过在静水中强制船舶摇荡来模拟其在不同波浪条件下的运动状态，计算船舶在不同运动状态下，船-桨-舵-舵附推力鳍系统中螺旋桨的推力、船体的阻力、螺旋桨的转矩。本文基于Overset网格技术对船桨推进系统旋转与纵摇（横摇）的耦合运动进行数值模拟，计算过程中考虑了重力的影响，对该船桨推进系统在纵摇运动（纵摇最大角度1°，周期10 s）、横摇运动（横摇最大角度5°，周期5 s）两种工况下的水动力性能进行计算和分析。船体纵摇运动的公式定义为：

图9为船桨推进系统在振荡运动状态下的运动示意图，图中标出了下文分析中会出现的四个时刻所对应的位置，即t/T=0.00（与t/T=1.00相同）、t/T=0.25、t/T=0.5、t/T=0.75。

图9 船体纵摇（横摇）运动示意图

4.1 纵摇下的船-桨-舵系统水动力分析

通过生成网格并进行边界条件的设置，采用船速1.220 m/s，螺旋桨转速10.141 r/min（与前面设置一致）。推力和转矩收敛曲线见图10和图11。

图10 带有舵附推力鳍的船桨舵系统在纵摇运动下推力值收敛曲线

图11 带有舵附推力鳍的船桨舵系统在纵摇运动下转矩值收敛曲线

由于船体进行规律性的运动，阻力与推力都是周期性变化，选取一个周期，取平均值得到船体阻力与螺旋桨推力和转矩。数值计算结果见表7。

表7 船-桨-舵系统水动力数值计算结果（纵摇）

纵摇状态下，将船-桨-舵-舵附推力鳍系统的计算结果与船-桨-舵系统的计算结果比较后发现，前者船体阻力增加1.11 N、螺旋桨的推力增加了0.22 N，螺旋桨的转矩从数据上看没有变化。计算结果表明，安装舵附推力鳍对螺旋桨的转矩没有明显的影响，船体阻力以及螺旋桨推力均有所增加。

4.2 横摇下的船-桨-舵系统水动力分析

横摇状态下，数值计算结果见表8，推力和转矩收敛曲线见图12和图13。

表8 船-桨-舵系统水动力数值计算结果（横摇）

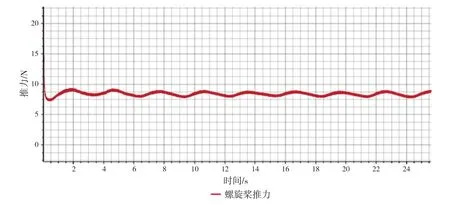
图12 带有舵附推力鳍的船桨舵系统在横摇运动下推力值收敛曲线

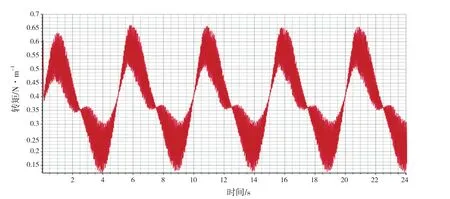
图13 带有舵附推力鳍的船桨舵系统在横摇运动下扭矩值收敛曲线

将船-桨-舵-舵附推力鳍系统的计算结果同船-桨-舵系统的计算结果比较后发现：前者船体阻力增加1.88 N，螺旋桨的推力增加0.09 N，螺旋桨的转矩从数据上看并没有变化。计算结果表明，安装舵附推力鳍对螺旋桨的转矩没有明显影响，船体阻力以及螺旋桨推力均有所增加。

5 结 论

本文进行了船-桨-舵系统以及船-桨-舵-舵附推力鳍系统的水动力计算，旨在通过计算安装舵附推力鳍的船舶在不同运动状态下螺旋桨的推力、转矩，并与静水工况下的船-桨-舵系统螺旋桨推力、转矩进行对比分析，获得船舶不同运动状态下舵附推力鳍的水动力性能，并得出如下结论：

（1）静水状态与运动状态下舵附推力鳍有助于提高螺旋桨效率。

（2）船体纵摇、横摇运动状态对于螺旋桨的效率影响较大，且船体阻力也会变大。

（3）本文采用强迫船体产生横摇、纵摇运动的方法来模拟船舶在波浪中的运动，与船舶在波浪中的真实运动有一定的区别。

在后续工作中，将尝试运用动态流体固体相互作用（DFBI，Dynamic Fluid Body Interaction）来模拟船舶在波浪中的六自由度摇荡运动，设置不同的波浪参数，使计算结果更接近于船舶在波浪中航行的真实情况。

［ 1 ］王超.船舶特种推进器与附加节能装置［M］.哈尔滨：哈尔滨工程大学出版社，2013：40-60.

［ 2 ］胡海洲，苏玉民，沈海龙，等.船体影响下舵附推力鳍的节能效果研究［J］.舰船科学技术，2016（5）：67-72.

［ 3 ］Carrica P M， Fu Huiping， Stern F.Computations of selfpropulsion free to sink and trim and of motions in head waves of the KRISO Container Ship（KCS）model［J］.Applied Ocean Research， 2011，33： 309-320.

［ 4 ］赵大刚.船-桨-舵-舵球式推力鳍系统水动力性能数值计算［D］.哈尔滨：哈尔滨工程大学，2012.

［ 5 ］Giulio Dubbioso， Roberto Muscari， Andrea Di Mascio.Analysis of the performance of a marine propeller operating in oblique flow［J］.Computer & Fluid，2013，75：86-102.

［ 6 ］Lin Z， Wang X， Yuan X， et al.Investigation and improvement of the staggered labyrinth seal［J］.Chinese Journal of Mechanical Engineering， 2015（2）：402-408.

［ 7 ］倪崇本.基于CFD的船舶阻力性能综合研究［D］.上海交通大学，2011.

［ 8 ］National Maritime Research Institute（NMRI）.Tokyo 2015-A Workshop on CFD in Ship Hydrodymics［EB/OL］.Tokyo，［December2-4，2015］.http：//www.t2015.nmri.go.jp/index.html.

［ 9 ］黄胜.船舶推进节能技术与特种推进器［M］.哈尔滨：哈尔滨工程大学出版社，2007.

［10］黄胜，郭春雨.船舶推进节能技术研究与进展［J］.舰船科学技术，2007（1）：27-32.

［11］郭春雨，黄胜，常欣.非定常流中桨后舵附推力鳍的数值模拟［J］.哈尔滨工程大学学报，2007（3）：259-262.

［12］郭春雨.螺旋桨与舵附推力鳍相互干扰水动力性能数值计算［D］.哈尔滨工程大学，2007.

［13］郭春雨，黄胜.面元法计算桨后舵附推力鳍水动力性能［J］.哈尔滨工程大学学报，2006（4）：501-504.

［14］郭春雨，黄胜.非线性涡格法预报桨后舵附推力鳍水动力性能［J］.华中科技大学学报（自然科学版），2006（6）：87-89.

Analysis of hydrodynamic performance of rudder with additional thrust f ns for moving ships

WANG Wen-quan1WANG Shi-yang1ZHANG Tian-tian2
(1.Marine Design & Research Institute of China, Shanghai 200011, China; 2.Dalian Vocational & Technical College, Dalian 116035, China)

The CFD simulations of the self-propulsion test with pitch and rolling for a 75 000 t model ship were carried out by the numerical wave tank technology and numerical towing tank technology based on RANSE.The resistance test and self-propulsion test simulations for the ship in calm water were firstly performed and compared with the model test results to preliminarily validate the CFD simulation method.Then, the self-propulsion tests for the model ships with or without rudders with additional thrust fins under the different motion modes were simulated to analyze the resistance and motion responses of the model ship, and the thrust and torque of the aft propeller, resulting in the relevant variation characteristics.The research can provide guidance and reference for the study and prediction of powering performance of ships in waves.

rudder with additional thrust fins; pitch; rolling; self-propulsion

U661.1

A

1001-9855（2016）06-0019-09

2016-04-18；

2016-07-19

王文全（1987-），男，博士，工程师，研究方向：船舶总体设计。王诗洋（1981-），男，硕士，高级工程师，研究方向：船舶总体设计。张天添（1986-），女，硕士，实验师，研究方向：船舶性能试验。

10.19423/j.cnki.31-1561/u.2016.06.019