VSC-HVDC附加频率极点配置控制器设计
2017-01-09朱显亮张英敏李兴源褚正超郭磊王渝红
朱显亮,张英敏,李兴源,褚正超,郭磊,王渝红
(四川大学电气信息学院,成都市 610065)
VSC-HVDC附加频率极点配置控制器设计
朱显亮,张英敏,李兴源,褚正超,郭磊,王渝红
(四川大学电气信息学院,成都市 610065)
为抑制柔性直流输电(voltage source converter-high voltage direct current, VSC-HVDC)低频振荡,提高柔性直流输电的输电能力,提出一种极点配置控制策略。利用改进的最小二乘旋转不变辨识算法,辨识出系统的开环传递函数。根据开环传递函数的根轨迹图,得到使其稳定的开环增益区间,进而得到较好增益下的闭环根轨迹极点,也就是期望极点。然后把得到的期望极点与配置的观测器极点结合起来,得到极点配置控制器。观测器减少工作量的同时,可以保证控制器较好的鲁棒性。为了显示控制器效果的优越性,利用经典根轨迹超前补偿设计法,设计出控制器与其进行对比。在PSCAD/EMTDC中的仿真结果表明,经典根轨迹法设计出的控制器效果不太明显,极点配置控制器可以较好地抑制VSC-HVDC在不同故障下的低频振荡,有较好的鲁棒性。
柔性直流输电;极点配置;根轨迹图;低频振荡;鲁棒性
0 引 言
柔性直流输电技术始于20世纪90年代末,其所具有的基于可关断器件和脉冲宽度调制(pulse width modulation, PWM)技术的电压源换流器(voltage source converter, VSC)使直流输电进入了崭新时代[1-2]。相对于传统直流输电技术而言,具有占地面积小、可以实现对有功与无功功率的同控制、可以对无源系统单独供电、谐波水平低等一系列优点[3]。因此,其在分布式发电并网运行,远距离输电,以及城市电网发展规划方面具有诸多优势。[4]
目前对于柔性直流输电低频振荡问题,相对于传统直流输电而言,其控制研究机理并不是太多。文献[5]采用的鲁棒控制法,对于低阶传递函数而言,计算工作量已经比较大。如果系统模型较大,传递函数阶数往往比较高,因此计算工作量会更大。文献[6]采用变参数法设计控制器,由于模型阶数较高,设计过程中需要调试控制器参数,工作量较大。文献[7]采用根轨迹法,由于辨识出的传递函数阶数比较高,这样造成计算量比较大。鉴于以上问题,本文采用极点配置法设计控制器。
本文采用改进最小二乘旋转不变辨识算法,得到系统的开环传递函数。利用其根轨迹图可以得到使其闭环传递函数稳定的开环增益值,然后得到较好增益值下的闭环极点。利用带观测器的极点配置法,把得到的期望极点与配置的观测器极点结合起来,得到极点配置控制器。为了显示其控制器的优越性,利用经典根轨迹法设计出控制器与其进行对比。经过电力系统仿真软件PSCAD/EMTDC仿真表明,极点配置控制器相对于经典根轨迹法控制器而言,可以较好地抑制系统不同扰动下的低频振荡,有较好的鲁棒性。
1 TLS-ESPRIT辨识原理
最小二乘旋转不变辨识算法(total least squares-estimation of signalparameters via rotational invariance techniques, TLS-ESPRIT)是一种改进的高精度辨识算法[8-12],其对信号单独分配子空间,相对于传统的Prony算法而言,具有更强的抗噪声抗干扰能力。ESPRIT的基本原理是通过采样,把得到的采样信号分解为一系列自相关与互相关的矩阵。并给信号单独分配子空间,减少采样信号间的耦合干扰,提高精度。然后分别计算信号的频率与衰减因子。最后再结合TLS得到信号的幅值与相位,进而得到系统的开环传递函数。
TLS-ESPRIT算法的具体步骤如下:
假设采样信号是由一系列正弦与白噪声信号组成
(1)
式中:t为采样信号实际含有的实正弦分量个数的2倍;Tk为采样周期值;ci=riejθi;ri、θi、σi、ωi分别为第i个振荡模态下的幅值、相位、衰减因子、角频率;ω(n)为白噪声信号频率。
把采样数据构造成Hankel矩阵
(2)
式中:X>t;Y>t;X+Y-1=D。
奇异值分解Hankel矩阵
Z=ΛUVΓ
(3)
式中:将矩阵Z的奇异值作为对角元素按大小排列,形成对角矩阵U;Λ为正交矩阵;矩阵V按照自身的奇异值大小被分解为信号子空间VS以及噪声子空间VN;Γ表示矩阵的共轭转置;矩阵Z幅值最大的t个奇异值的特征向量为矩阵VS的列向量。
假设VS去掉最后1行的矩阵为V1,VS去掉第1行的矩阵为V2。再分解由V1、V2构成的矩阵
(4)
式中:Φ和Θ为正交矩阵;Ψ为对角矩阵。
(5)
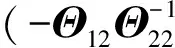
(6)
(7)
(8)
在系统进入稳定运行后,通过在整流侧添加不影响系统线性化的小幅阶跃扰动得到发电机1、3的频率偏差f1,再取没添加阶跃扰动时发电机1、3的频率偏差f2,然后两者作差得到Δf=f1-f2。利用上述介绍的最小二乘旋转不变辨识算法辨识出系统的开环传递函数为
(9)
整流站VSC1的控制方式为定有功功率(PS1=200 MW)与定无功功率(QS1=120 MV·A),逆变站VSC2的控制方式为定直流电压(US2=360 kV)与定无功功率(QS2=-120 MV·A)。从左侧系统到右侧的输送功率为600 MW,其中交流系统输送功率为400 MW,直流系统输送功率为200 MW,VSC-HVDC的四机模型如图1所示。
2 极点配置控制器设计
2.1 系统根轨迹图分析
根轨迹法设计控制器是建立在改变系统根轨迹的基础上,是通过在系统开环传递函数中增加极点与零点,迫使根轨迹经过s平面内希望的极点的一种方法。假设控制系统的开环传递函数为G(s),输出为控制器的输入信号,控制器传递函数为Gc(s),则加入控制器后系统的闭环方框图如图2所示。
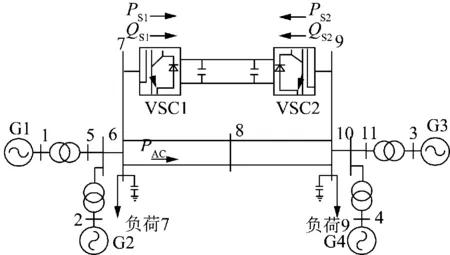
图1 柔性直流输电拓扑结构图

图2 控制系统
在MATLAB中绘制出系统开环传递函数的根轨迹图,如图3所示。
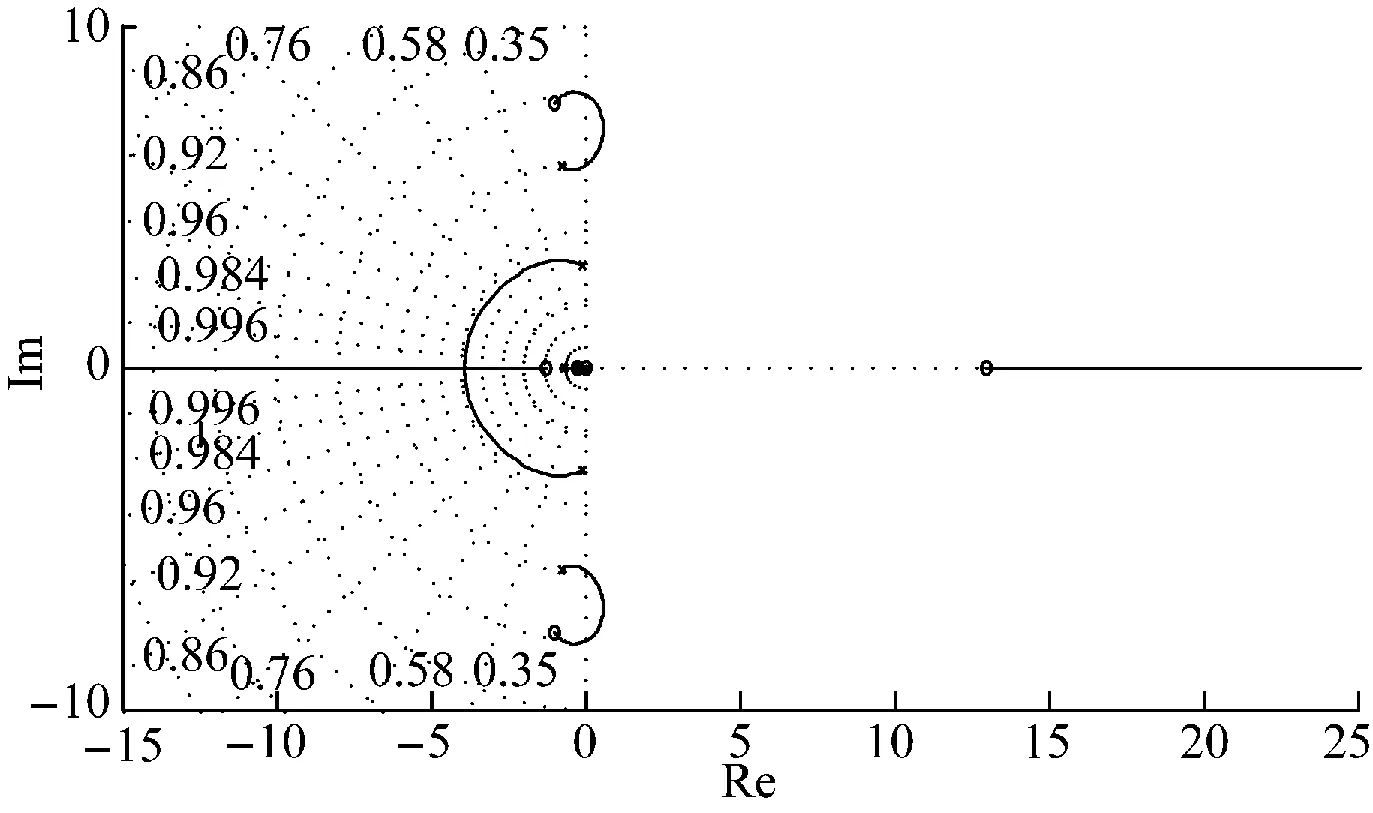
图3 系统根轨迹图
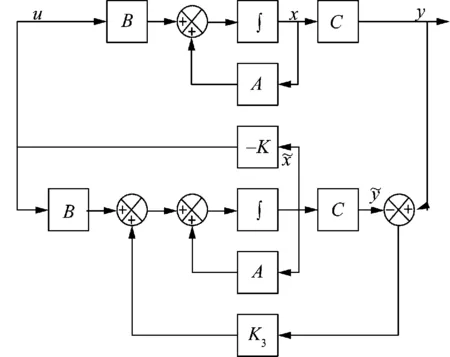
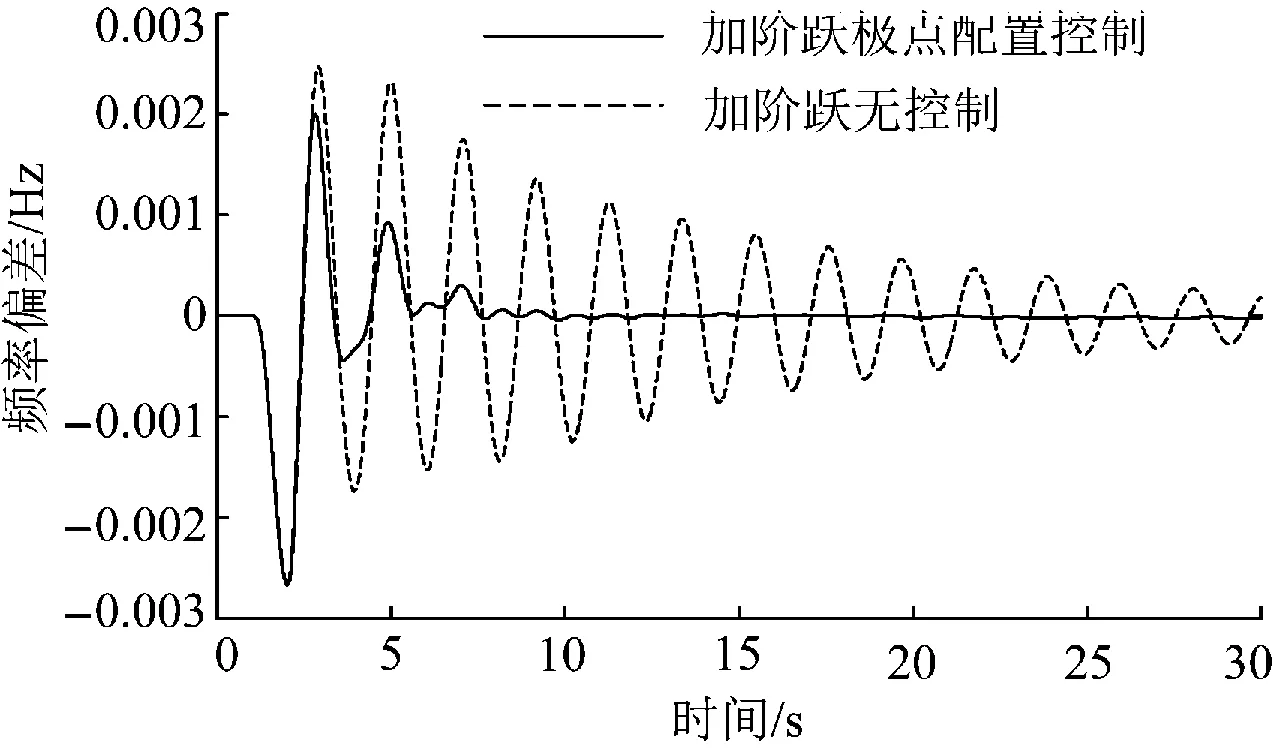
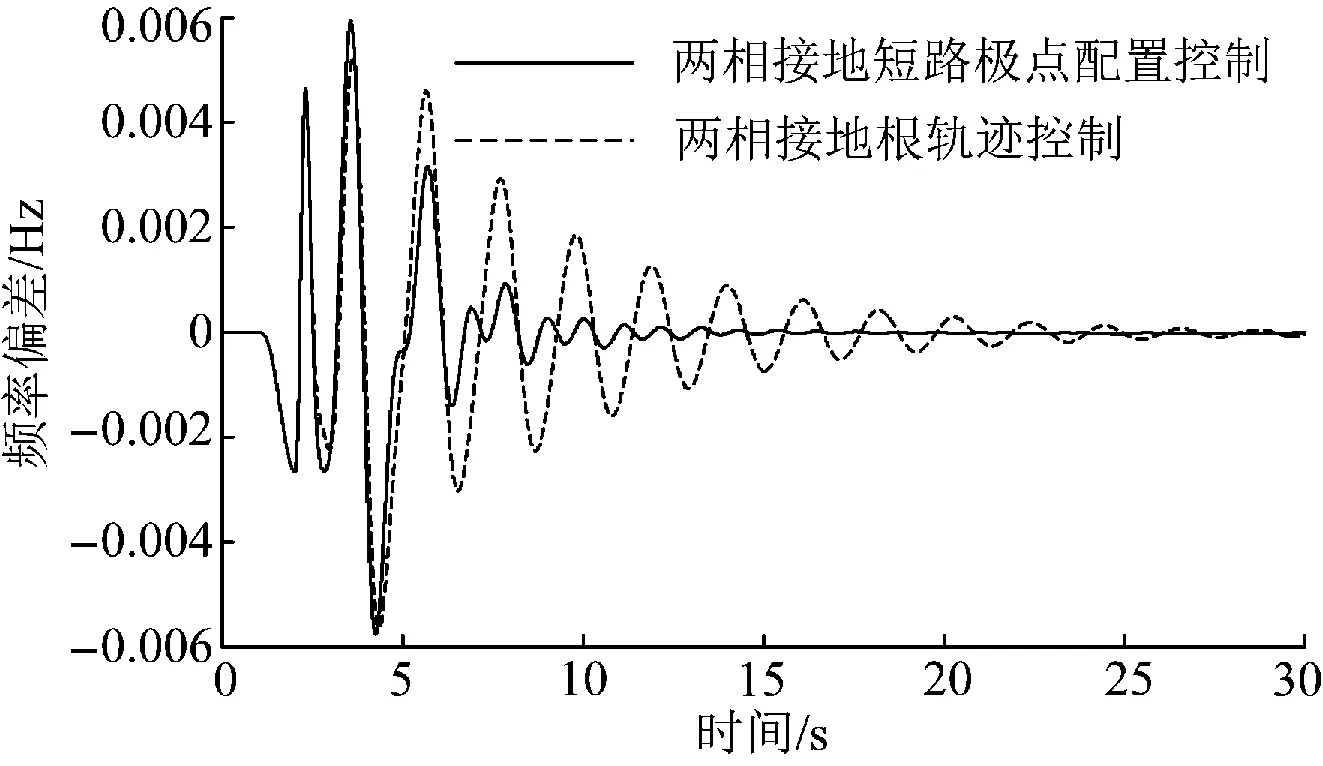
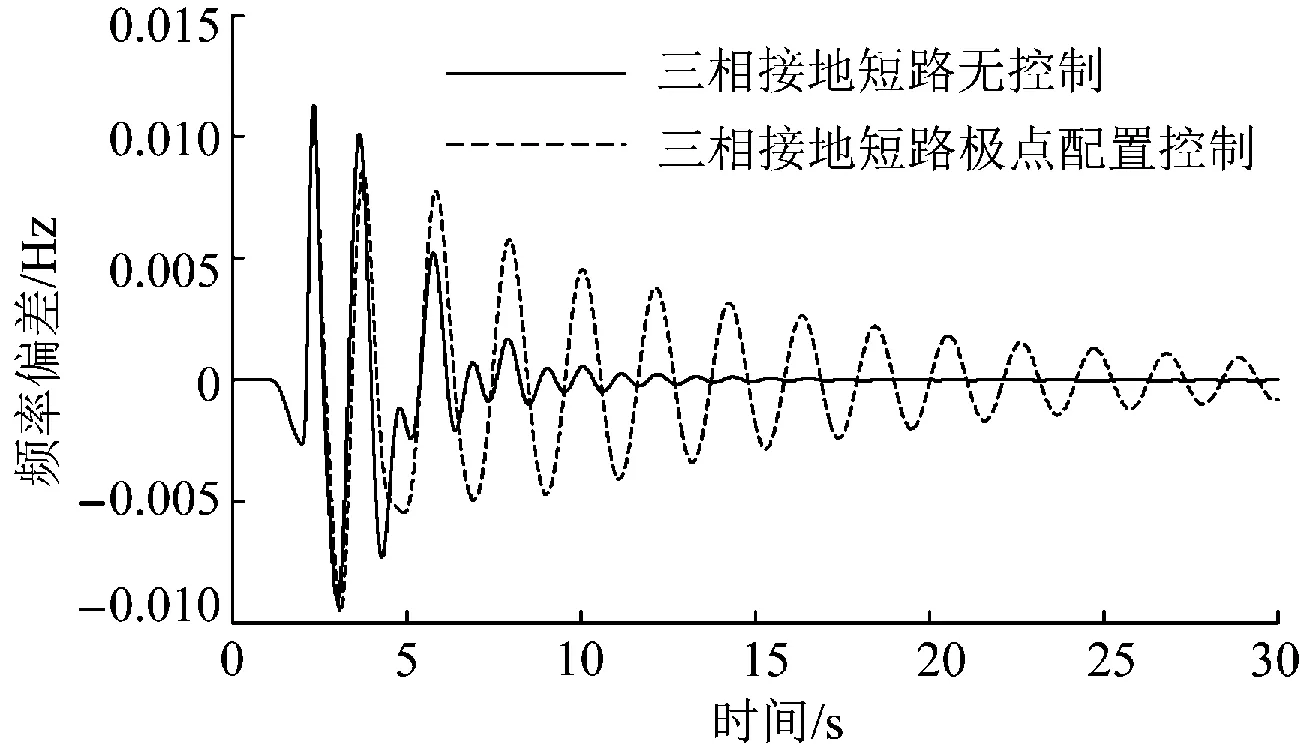
通过以上根轨迹图可以得出当系统的开环增益0 2.2 带状态观测器的极点配置控制原理 假如控制系统特征方程[15]为: (10) y=Cx+Du (11) 取VSC-HVDC系统控制信号为 u=-Kx (12) 其中K为状态反馈增益矩阵。 (13) 则系统向量动态特性由矩阵A-KC的特征值决定,如果所选的矩阵A-BK的特征值使得系统向量的动态特性渐近稳定且足够快,则任意系统向量都将以足够快的速度趋近于0(原点)。也就是说可以确定系统增益矩阵K,以产生期望的矩阵A-BK。 现在定义M=A-BK,则所期望的特征方程为 (s-μ1)(s-μ2)…(s-μn)=sn+α1 sn-1+ (14) 由于凯来-哈密尔顿定理阐明M应满足其自身的特征方程,所以 φ(M)=Mn+α1Mn-1+…+αn-1M+αnI=0 (15) 利用方程(14)可得确定状态反馈的增益矩阵K的爱克曼方程: (16) 根据上述得到系统闭环传递函数的期望极点。把期望极点代入式(13)中,解爱克曼方程(15),就可以得到使A-BK构成一个逐渐稳定矩阵的K值。 由于系统的真实状态无法准确测量,所以引入观测器,将观测到的状态再次用于反馈。这样在节省工作量的同时,还能保证系统的可控性[16-18],从而设计出带观测器的极点配置控制器。基于极点配置的状态-观测反馈控制系统如图4所示。 图4 基于极点配置控制器的状态-观测反馈控制系统 由图3可得观测器状态方程为: (17) (18) 为了得到观测器的误差方程,令方程(10)减去方程(17)可得: (19) (20) 观测器误差向量动态特性由矩阵A-K3C的特征值决定,如果所选的矩阵A-BK3的特征值使得系统向量的动态特性渐近稳定且足够快,则任意系统向量都将以足够快的速度趋近于0(原点)。也就是说可以确定系统增益矩阵K3,以产生期望的矩阵A-BK3。 现在定义N=A-BK3, 则所期望的特征方程为 (s-δ1)(s-δ2)…(s-δn)=sn+φ1sn-1+ φ2sn-2+…+φn-1s+φn=0 (21) 由于凯来-哈密尔顿定理阐明N应满足其自身的特征方程,所以 φ(N)=Nn+φ1Nn-1+…+φn-1N+φnI=0 (22) 利用方程(22)可得确定状态反馈的增益矩阵K3的爱克曼方程 (23) 根据上述2.1得到了观测器期望极点。把观测器期望极点代入上式(21)中,解爱克曼方程(23),就可以得到使A-BK3构成一个逐渐稳定矩阵的K3值。 (24) 将方程(24)代入方程(18)的拉普拉斯变换式得极点配置控制器-状态观测器传递函数 (25) 2.3 控制器参数设计 通过辨识得到的系统开环传递函数,根据2.1与2.2节介绍的控制器设计原理最终得到极点配置控制器。 (26) 在运行范围内的VSC的运行点,可以在PQ平面的任何一个象限内移动,这就相当于一个无转动惯量的同步电机。所以VSC能够独立地控制与交流系统交换的有功功率和无功功率,VSC-HVDC之所以可以同时调整系统的有功与无功功率,主要是VSC采用了dq轴的解耦控制法,VSC1的解耦控制图如图5所示。 极点配置控制器安装在柔性直流输电系统整流侧的定有功功率控制处,以发电机1、3的频率偏差为输入,附加有功信号为输出。通过调整直流侧功率,使其快速恢复稳定性。其控制结构如图6所示。 设计完极点配置控制器后,为了比较其控制器的效果,利用经典根轨迹超前补偿法,设计出根轨迹控制器,但设计工作量相对于带观测器的极点配置控制器来说较大,根轨迹控制器也安装在整流侧直流定有功功率处,其结构与极点配置控制器结构相同,结构如图7所示。 图5 VSC1 dq解耦拓扑图 图6 极点配置控制器结构图 Fig.6 Pole assignment controller structure 图7 根轨迹法控制器结构图 Fig.7 Root locus method controller structure 把上述设计好的极点配置控制器安装在图6所示的结构中,根轨迹控制器安装在图7所示的结构中。在PSCAD/EMTDC搭建好的模型中,添加不同的扰动进行仿真,取发电机1、3的频率偏差Δf13进行观测。 3.1 扰动1 2 s时在整流侧直流定功率处添加3倍阶跃扰动,使系统发电机的频率上升到4 pu,仿真如图8~9所示。 图8 加阶跃有控制器与无控制器模态对比图 图9 加阶跃根轨迹控制器与极点配置控制器模态对比图 3.2 扰动2 2 s时在逆变侧高压母线处发生单相接地故障,故障时间为0.1 s,仿真如图10~11所示。 图10 单相接地短路有控制器与无控制器模态对比图 图11 单相接地短路根轨迹控制器与 3.3 扰动3 2 s时在逆变侧高压母线处发生两相接地故障,故障时间为0.1 s,仿真如图12~13所示。 3.4 扰动4 2 s时在逆变侧高压母线处发生三相接地故障,故障时间为0.1 s,仿真如图14~15所示。 图12 两相接地短路有控制器与无控制器模态对比图 图13 两相接地短路根轨迹控制器与极点配置控制器模态对比图 图14 三相接地短路有控制器与无控制器模态对比图 由图8~9可知,本文设计的极点配置控制器可以较好地抑制系统发生阶跃扰动时的振荡,有较好的鲁棒性,而经典根轨迹法设计的控制器效果不太明显,即鲁棒性较差。同样由图10~11可知,极点配置控制器抑制系统由单相接地故障引发振荡的效果较经典根轨迹控制器明显。图12~13可以得出在系统发生两相接地短路时,极点配置控制器的效果依然较经典根轨迹控制器明显。图14~15显示系统在发生三相接地故障时,本文设计的极点配置控制器抑制振荡的效果较经典根轨迹控制器好。综上可知,极点配置控制器可以抑制不同故障下系统发生的低频振荡,适应性较好,即有较好的鲁棒性。而经典根轨迹法控制器虽然也可以抑制系统不同故障下的低频振荡,但相对于极点配置控制器来说,效果较差,即鲁棒性较差。 图15 三相接地短路根轨迹控制器与极点配置控制器模态对比图 本文针对VSC-HVDC低频振荡问题,设计了一种极点配置控制器。利用改进最小二乘旋转不变辨识算法,辨识出系统的开环传递函数。根据其根轨迹图得到使其闭环传递函数稳定的增益范围,从而选择较好的增益值。使系统快速恢复稳定,得到系统的闭环传递函数极点,即期望极点。因为此时得到的纯增益相当于PID控制器,PID控制器对运行方式比较敏感,改变运行方式,可能会失去效果。为了提高控制器的适应性,且系统的真实状态往往是无法测量的,所以引入状态观测器。减少了工作量,得到极点配置控制器,保证了控制器较好的鲁棒性。为了显示极点配置控制器控制效果的优越性,设计了根轨迹控制器与其进行对比。经过电力系统仿真软件PSCAD/EMTDC仿真表明,极点配置控制器可以较好地抑制系统在不同故障下的低频振荡,适应性较好,即有较好的鲁棒性。根轨迹控制器虽有效果,但相对于极点配置控制器来说,其效果不太明显。另外,本文设计的控制器,可以减少工作量,适用于高阶传递函数,切合实际。 [1]文俊,张一工,韩民晓,等.轻型直流输电:一种新一代的HVDC技术 [J].电网技术,2003,27(1):47-51. WEN Jun,ZHANG Yigong,HAN Minxiao,et al.HVDC based on voltage source converter:a new generation of HVDC technique [J]. Power System Technology,2003,27(1):47-51. [2]徐政,等著.柔性直流输电系统 [M].北京:机械工业出版社,2012. [3]马玉龙,马为民,陈东,等.舟山多端柔性直流工程系统方案[J].电力建设,2014,35(3):1-6. MA Yulong,MA Weimin,CHEN Dong,et al.System scheme of zhoushan multi-terminals VSC-HVDC project[J].Electric Power Construction,2014,35(3):1-6. [4]肖峻,李思岑,黄仁乐,等城市电网分区柔性互联选址方法及示范应用[J].电力建设,2016,37(5):10-20. XIAO Jun,LI Sicen,HUANG Renle, et al.Siting method and demonstration application of flexible interconnection in urban power grid partition[J].Electric Power Construction,2016,37(5):10-20. [5]张立奎,张英敏,李兴源.柔性直流附加鲁棒阻尼控制器设计[J].现代电力,2015,32(2):70-75. ZHANG Likui,ZHANG Yingmin,LI Xingyuan.Design of additional robust damping controller for VSC-HVDC [J].Modern Electric Power,2015,32(2):70-75. [6]马锋,李国杰,阮思烨.基于线性变参数方法的 VSC-HVDC变增益附加阻尼控制器设计[J].电网技术,2009,33(2):74-76. MA Feng,LI Guojie,RUAN Sihua.Desigen of VSC-HVDC supplementary damping controoller using linear parameter varying approach [J].Power System Technology,2009,33(2):74-76. [7]常勇,李晶,张海燕.基于广域信号的柔性直流输电附加阻尼控制 [J].中国电力,2009,42(10):33-38. CHANG Yong,LI Jing,ZHANG Haiyan.Design of VSC-HVDC supplementary controller based on wide-area signals [J]. Electric Power,2009,42(10):33-38. [8]胡志冰,蔡国伟,刘铖.基于FastICA和Prony算法的低频振荡参数辨识 [J].电测与仪表,2014,51(18):39-43. HU Zhibing,CAI Guowei,LIU Cheng.Parameter identification of low frequency oscillion based on fast ICA and prony algorithm [J].Electrical Measurement & Instrumentation,2014,51(18):39-43. [9]TRIPATHY P,SRIVASTAVA S C,SINGH S N.A modified TLS-ESPRIT based method for low-frequency mode identification in power systems utilizing synchrophasor measuerments [J].IEEE Transactions on Power Systems,2011,26(2):719-727. [10]魏亮,王渝红,李兴源,等.高压直流输电送端孤岛运行附加频率控制器设计[J].电力自动化设备,2015,36(1):143-148. WEI Liang,WANG Yuhong,LI Xingyuan,et al.Design of additional frequency controller for islanded sending-end operation of HVDC system [J].Eletric Power Automation Equipment,2015,36(1):143-148. [11]徐遐龄,林涛,张帆,等.基于 TLS-ESPRIT 的低频振荡负荷参与程度量化分析[J].电网技术,2012,36(11):109-113. XU Xialing , LIN Tao , ZHANG Fan , et al . TLS-ESPRIT based quantitative analysis on participating degree of load in low-frequency oscillation[J].Power System Technology,2012,36(11):109-113. [12]王曦,李兴源,王渝红,等.基于TLS-ESPRIT辨识的多直流控制敏感点研究[J].电力系统保护与控制,2012,40(19):121-125. WANG Xi,LI Xingyuan,WANG Yuhong,et al.Analysis on controllability sensitive points of multi-HVDC systems based on TLS-ESPRIT method [J].Power System Protection and Control,2012,40(19):121-125. [13]赵睿,李兴源,刘天琪,等.抑制次同步振荡和低频振荡的多通道附加阻尼控制器设计[J].电力系统自动化设备,2014,34(3):89-92. ZHAO Rui,LI Xingyuan,LIU Tianqi,et al.Design of multi-channel DC supplementary damping controller for subsynchronous and low- frequency oscillation suppression[J] . Electric Power Automation Equipment,2014,34(3):89-92. [14]汤华,王渝红,魏亮,等.HVDC孤岛运行附加频率鲁棒控制器设计[J].电网技术,2016,40 (4):1-7. TANG Hua,WANG Yuhong,WEI Liang,et al. An additional frequency robust controller for HVDC transmission system under islanding operation [J].Power System Technology,2016,40 (4):1-7. [15]KATSUHIO O.现代控制工程(第四版) [M].卢伯英,于海勋,译.北京:电子工业出版社,2007. [16]李天云,张志华,陈峰,等.基于扩张状态观测器和 Terminal 滑模的 HVDC 非线性鲁棒控制器设计[J].电网技术,2012,36(10):190-195. LI Tianyun,ZHANG Zhihua, CHEN Feng,et al.Design of nonlinear robust controller of HVDC power transmission system based on extended state observer and terminal sliding mode control[J].Power System Technology,2012,36(10):190-195. [17]张洪帅,王平,韩邦成,等.基于模糊滑模观测器的磁悬浮高速永磁同步电机转子位置检测方法[J].电工技术学报,2014,29(7):147-153. ZHANG Hongshuai,WANG Ping,HAN Bangcheng,et al.Rotor position measuring method for magnetic levitation high speed PMSM based on fuzzy sliding mode observer[J].Transactions of China Electrotechnical Society,2014,29(7):147-153. [18]李宾,姚文熙,杭丽君,等.基于状态观测器的LCL滤波器型并网逆变器状态反馈最优化设计[J].电工技术学报,2014,29(6):80-90. LI Bin,YAO Wenxi,HANG Lijun,et al.Optimized design of state variable feedback of grid-connected inverter with LCL-filter based on state observer[J].Transactions of China Electrotechnical Society,2014,29(6):80-90. 郭磊( 1990) ,男,硕士研究生,主要研究方向为高压直流输电、电力系统稳定与控制; 王渝红(1971),女,教授,硕士生导师,研究方向为高压直流输电、电力系统稳定与控制、新能源并网方式。 (编辑 刘文莹) An Additional Frequency Pole Assignment Controller for VSC-HVDC ZHU Xianliang , ZHANG Yingmin , LI Xingyuan, CHU Zhengchao, GUO Lei,WANG Yuhong (School of Electrical and Information, Sichuan University, Chengdu 610065, China) In order to suppress the voltage source converter-high voltage direct current (VSC-HVDC) low frequency oscillation and improve its transmission capacity, this paper proposes a control strategy for pole assignment. We use the improved TLS-ESPRIT recognition algorithm to identify the open-loop transfer function of the system. According to the root locus diagram of the open-loop transfer function, we get the open-loop gain interval which makes it stable, and then get the closed-loop root locus poles under a better gain which are desired poles. And then we combine the desired poles with the configured observer poles to obtain a pole assignment controller. The application of the observer controller can not only reduce the work load but also have better robustness. To show the superior effect of the proposed controller, we adopted the classical root locus advance compensation method to design the controller and compared it with the proposed controller. The simulation results in PSCAD/EMTDC show that the effect of the controller designed by the classical root locus method is not obvious, while the proposed pole assignment controller can better restrain low frequency oscillation of VSC-HVDC under the different malfunctions, and therefore has better robustness. VSC-HVDC; pole assignment; root locus diagram; low frequency oscillation; robustness 国家电网公司大电网重大专项资助项目课题(SGCC-MPLG001-027-2012)。 TM 72 A 1000-7229(2016)10-0086-07 10.3969/j.issn.1000-7229.2016.10.012 2016-05-25 朱显亮(1987),男,硕士研究生,主要从事电力系统稳定与控制,高压直流输电方面的研究; 张英敏(1974),女,副教授,研究方向为电力系统分析计算与稳定控制; 李兴源(1945),男,教授,博士生导师,研究方向为电力系统稳定与控制、高压直流输电、新能源并网方式; 褚正超(1992),男,硕士研究生,主要研究方向为高压直流输电、电力系统稳定与控制;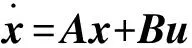







3 仿真验证




4 结 论
