努力扰动需求下回收再制造闭环供应链协调研究

何建佳，蒋雪琳，徐福缘(上海理工大学.管理学院;b.超网络研究中心（中国），上海200093）

努力扰动需求下回收再制造闭环供应链协调研究

何建佳a,b，蒋雪琳a，徐福缘a,b
(上海理工大学a.管理学院;b.超网络研究中心（中国），上海200093）

努力水平是影响供应链协调的一个重要决策变量。文章研究了努力水平影响需求环境下回收再制造闭环供应链的努力水平和订货量的同时协调问题，建立了制造商与零售商之间的博弈模型，探讨在集中化模式和分散化模式下最优努力水平和最佳订货量应当满足的参数条件。在此基础上，构建限制性补贴契约来实现闭环供应链回收再制造的努力水平和订货量同时协调，并分析影响整个闭环供应链协调的影响因素及相关因素之间的变动关系。通过算例分析，论证了模型的有效性和契约的合理性。

闭环供应链；努力水平；供应链契约；限制性补贴；再制造；协调

0 引言

闭环供应链环境下的废旧产品回收再制造管理成为企业界和学术界广泛关注的重要议题。为有效地实现闭环供应链上废旧产品的回收再制造管理，关键在于如何协调链上各节点企业之间的相关利益关系，使链上各节点企业的个体利益与整体利益达成一致。由于供应链契约是协调供应链的有效手段，也是链接供应链上各节点企业的纽带，它通过提供合适的信息资源和激励措施，保证买卖双方协调，优化销售渠道绩效的有关条款[1]。文献[2-5]也明确地论证了供应链契约协调机制能够有效地协调供应链上各节点企业的相关利益，改善企业经营绩效，实现整个供应链的协调运作。因此，运用供应链契约来协调废旧产品回收再制造闭环供应链节点企业间利益关系具有重要的理论价值和实践意义。

零售商的努力水平是影响市场需求的重要决策因素，它能够有效地改善闭环供应链各节点企业的经营绩效。因此，在闭环供应链废旧产品回收再制造的协调问题上，应当考虑努力水平影响因素。在已有研究的基础上，本文在考虑市场需求是随机的且零售商努力水平影响需求的前提下，建立了废旧产品回收再制造闭环供应链上制造商与零售商之间的主从博弈模型，讨论了限制性补贴契约下闭环供应链订购量与努力水平同时协调问题以及相关影响因素之间的变动关系，有效地实现整个闭环供应链的协调运作。

1 问题描述、参数定义与假设条件

Savaska等通过对制造商、零售商以及第三方回收三种回收模式的研究，建立Stackelberg博弈模型，提出在满足前提假设条件下闭环供应链废旧产品回收采取零售商回收的方式获得的收益最佳[6]。鉴于此，研究零售商回收模式下制造商与零售商组成的两级闭环供应链废旧产品回收再制造问题。采取零售商回收模式的闭环供应链回收模型结构如图1所示：

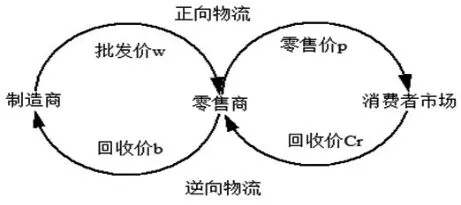
图1闭环供应链废旧产品回收模型结构

模型中涉及的符号参数定义，如表1所示：

表1 模型相关的参数符号及定义描述

根据上述问题及参数符号定义描述，模型的基本假设条件如下：

(1)闭环供应链回收再制造系统是由一个制造商、一个零售商和消费者市场构成，系统中的各成员均以自身利益最大化为原则。制造商和零售商采取Stackelberg博弈模型进行独立决策；

(2)本文考虑零售商的努力水平为决策变量，零售商的努力水平为e，e≥0，其努力成本为u(e)，且u(0)=0，u'(e)＞0，u''(e)＞0；

(3)假定市场需求和废旧产品回收数量受零售商努力水平大小的影响,市场需求x是随机变量，其概率密度函数及概率分布函数分别为f(x |e) 和F(x |e) ，且

(4)从制造商角度来看，制造商使用新原材料制造的单位产品生产成本为c0，制造商回收再制造成本为cm，c0＞cm；制造商回收节约的单位成本为 c1，即c1=c0-cm＞0；制造商向零售商回收废旧品的单位成本为b，0＜b＜c1，即制造商回收节约成本大于回收价格，不满足该条件研究闭环供应链回收再制造问题是没有实际意义的；

(5)对于零售商来说，其单位产品的零售价格为p，且为外生变量；零售商的订货量或制造商的生产量为Q，

(6)文献[7]假设闭环供应链新产品与再制造产品是存在差异的，且消费者对再制造产品的认可度不高于对新产品的认可度；而本文则考虑制造商使用新原材料和废旧材料再制造加工生产的产品质量无差异；

(7)制造商和零售商是风险中性的。

2 闭环供应链回收再制造契约模型分析

2．1 集中化闭环供应链系统模型

在集中化系统模型决策中，生产制造商与零售商统一决策，追求整个供应链的利润最大化，即确定最优努力水平e*和最佳订货量Q*，在上述问题条件和参数设计的基础上，可知制造商、零售商的期望利润为：

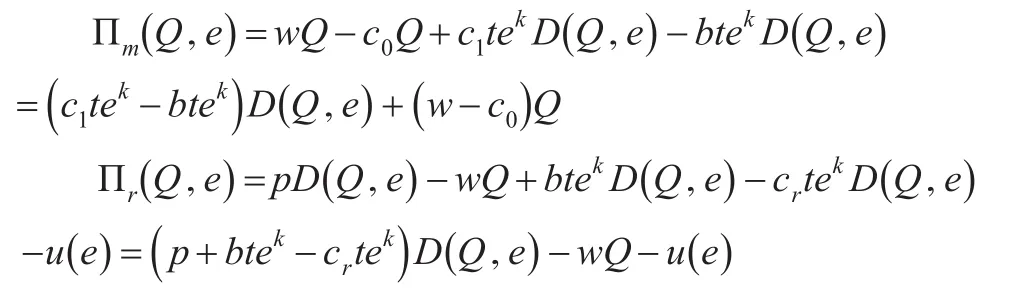
由此可知，集中化闭环供应链的最大化期望利润为：

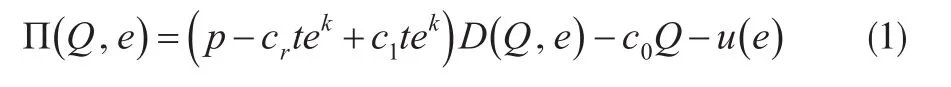
对式(1)求一阶、二阶偏导数：

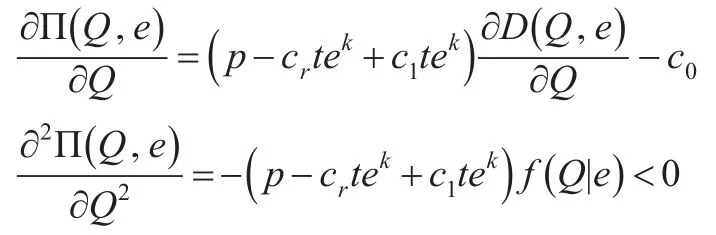
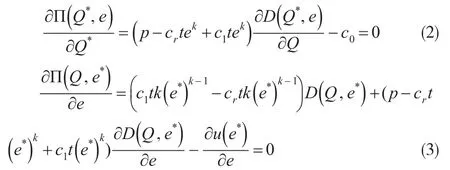
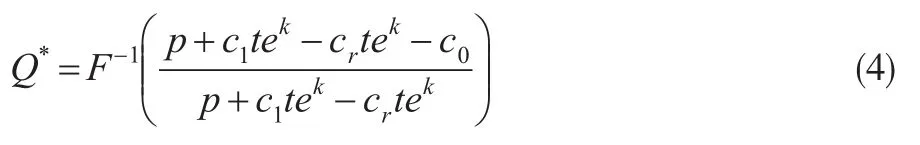
为实现闭环供应链协调，式(2)和式(3)是制造商通过契约协调供应链的必要条件，必须满足这两个约束条件。

2．2 分散化闭环供应链系统模型

在分散式供应链模型系统决策下，制造商和零售商独自进行决策经营使其获得的利润最大化，零售商最大期望总利润为：

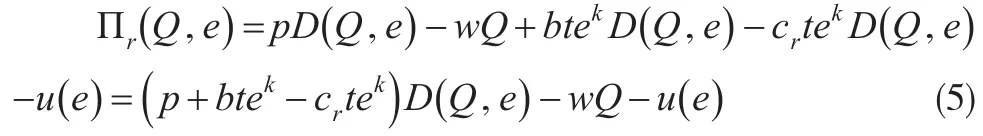
对式(5)求一阶偏导数，且零售商的最优努力水平应满足：

将式(6)与式(3)进行比较可知，只有当c1=b时，式(6)才能成立。但是，这与前提条件0＜b＜c1相矛盾，并且当c1=b时，讨论闭环供应链回收再制造问题是没有任何实际意义的，且Πr(Q ，e)＜Π(Q ，e)，即闭环供应链的系统收益没有达到最优。然而，当c1=b时，其实质就是单纯的批发价契约，在这种契约下，制造商总能从中获益，而零售商却不能获得相应的效益。同时表明，由于受到双边际化效应的影响，单纯使用批发价契约很难使闭环供应链达到完善的协调状态，不易实现企业与供应链整体效益的协调一致。这一结果产生的原因是零售商独自承担努力水平下的努力成本。

综上分析，可得出这样的结论：在零售商努力水平影响随机需求的前提下，传统的批发价契约不能实现闭环供应链协调，为解决这一问题，引入限制性补贴来讨论对批发价契约的演化契约模型，找出问题的解决方案。

2．3 限制性补贴契约模型

为了实现闭环供应链协调，考虑通过引入限制性补贴的策略来缓解零售商经营风险。在上述问题分析的基础上，构建限制性补贴契约模型，协调闭环供应链各节点企业利益，达到优化均衡。制造商在订立批发价契约时，确定期望的目标订货量H，当零售商高出目标订货量H的产品数量给予一定的数量补贴,刺激零售商增加订货量，即n，n＞0。由于废旧产品用于再制造能够降低生产制造商的生产成本，增加经营收益。所以，制造商为了刺激零售商在回收废旧产品过程中的积极性，根据回收市场的具体情况，确定一个最低的废旧产品回收的目标数量T，对于高出T的部分给予零售商补贴回馈m，m＞0。从而激励零售商回收废旧产品。在上述条件下，零售商的最大期望利润为：

引入限制性补贴的演化契约后，零售商的努力水平应满足的条件为：

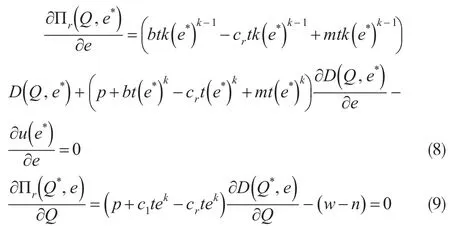
比较式(2)、(3)与式(8)、(9)可知，当m=c1-b，n=w-c0时，上式才能成立，才可以实现个体利益与整体利益一致。因此，此时零售商的最佳订货量Q1*为：

零售商期望的最大化利润为：

因此，综上分析可认为，在零售商努力水平影响需求约束前提下，通过限制性补贴契约，能够实现闭环供应链整体的协调运作，制造商也可以通过限制性补贴(w ，m，n)契约有效控制零售商，达到任意的利润值；并且如果制造商固定补贴参数m=c1-b，n=w-c0时，可获得最佳期望收益。

3 模型优化方法

根据上述的分析过程可知，通过引入限制性补贴契约研究，能够实现闭环供应链的协调，并且可以确保分散化闭环供应链系统零售商的最佳订货量和最优努力水平与集中化闭环供应链系统模式的相一致。因此，模型的优化问题变为：寻求最佳订货量Q*和最优努力水平e*，使整个闭环供应链的利润最大化。

假设市场需求满足x=z(e)+ξ的加法形式，其中，z(e)连续、非负且二级可微。易知，z(e)是努力水平e的增函数，且为凹函数，即z'(e)＞0，z''(e)≤0，也就是零售商努力水平的边际效应递减。其中ξ是独立于e的随机变量，其概率密度函数用 f(ξ)来表示，F(ξ)表示ξ的分布函数。此时，市场需求的概率密度函数和分布函数分别表示为：

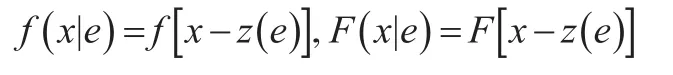
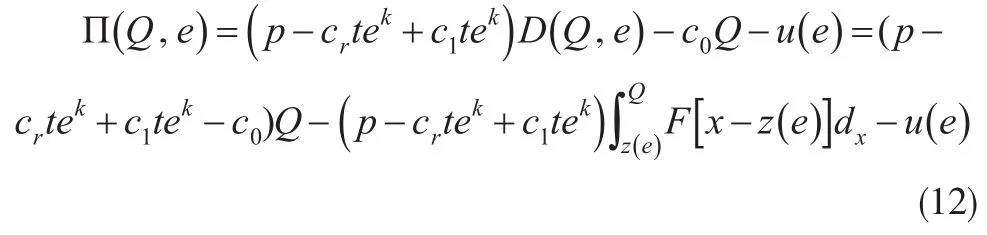
由式(12)可知，对于给定的努力水平e，其最佳订货量Q*应满足条件：

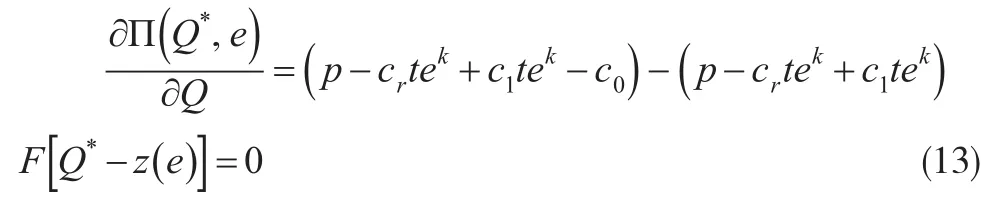
可推出：

将式(14)和ξ=x-z(e)代入式(12)，化简整理可得：

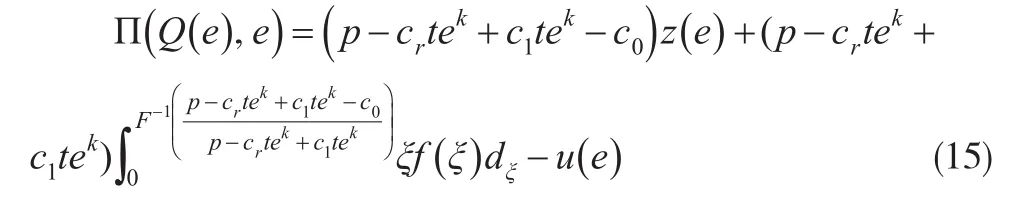
此时，Π(Q (e)，e)只有一个决策变量e，即模型的优化问题变为：寻求最优的努力水平e*，使Π(Q (e)，e)的值最大。为了便于分析，假设z(e)=λe，λ＞0，λ为零售商努力水平为e时市场需求的需求弹性敏感系数。ξ为区间[α，β]上的均匀分布，即ξ～[α ，β]。可知，ξ的密度函数、分布函数及反函数分别表示为：

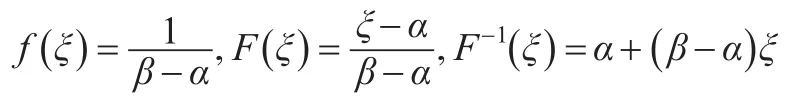
因此，式(15)可整理为：

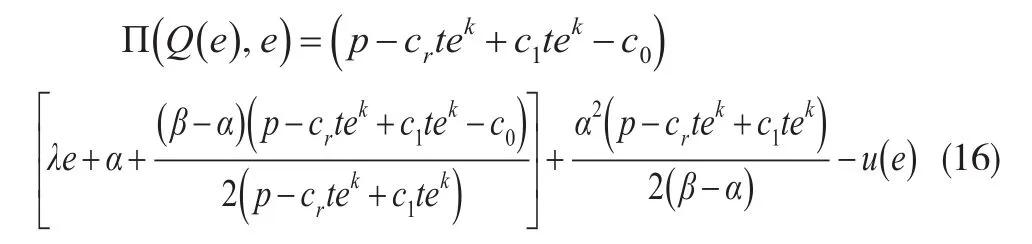
此时，最优努力水平e*应满足：

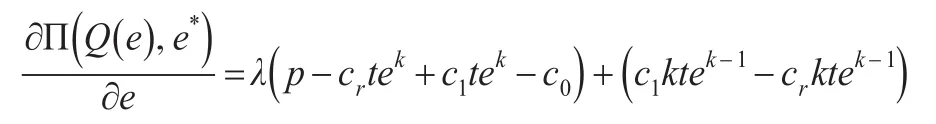
当零售商的努力水平e满足约束条件(17)，就能够获得一个相应的最佳订货量Q*满足式(14)，此时就能够得到整个闭环供应链的最优决策(e*，Q*)，从而，达到供应链的整体协调运作。

4 算例数值分析

根据闭环供应链的约束条件和实际情况，为了便于分析，试对上述公式进行简化，假设 p=10，w=8，c0=5，cm=2，c1=c0-cm=3，cr=1，b=2，k=0.5，λ=1，t=1，u(e)=5e+α=0，β=100即ξ～[0 ，100]。根据上述的分析过程，在实施限制性补贴契约条件下，制造商从零售商处回收废旧产品用于再制造环节中，将上述假设条件代入努力水平e满足的条件式(17)，可以得到零售商的最优努力水平e*，即最优努力水平e*=56.25。由于最佳订货量应当满足：

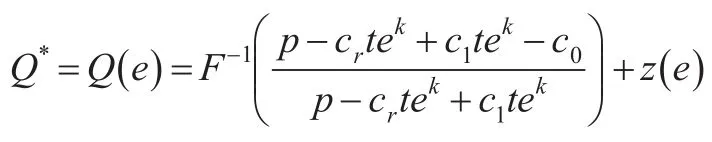
所以，将 e*=56.25代入上式，可得最佳订货量Q*=136.25。也可得到，制造商固定补贴参数m=c1-b，n=w-c0，即m=1，n=3。

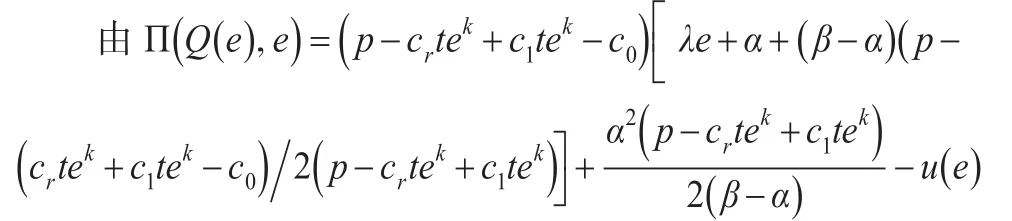
可得供应链利润Π(Q*，e*)=800。此时，可以得到整个闭环供应链的最优决策(e*，Q*)为(5 6.25，136.25)。

运用Matlab软件绘图分析可知，零售商的努力水平e与零售商的订货量Q呈正比例变动关系以及零售商的努力水平e与集中化闭环供应链整体利润Π(Q ，e)也同样呈正比例变动关系，如图2和图3所示。从图2可以看出，当e*=56.25时，最佳订货量Q*=136.25；但是，从图3中可知，当e*=56.25时，供应链利润Π(Q*，e*)=800，供应链利润却不是最大值，而是随着努力水平e的增加而一直呈现上升的状态，其具体原因有待进一步探讨，也从另一方面说明：当努力水平与订货量同时协调的情况下，供应链利润不一定达到最大值。

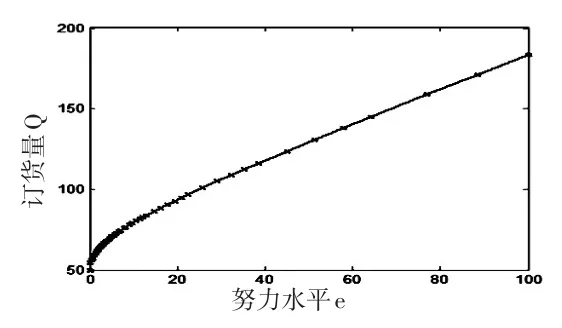
图2努力水平e与订货量Q的关系图

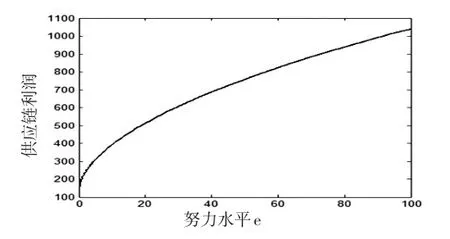
图3努力水平e与供应链利润Π(Q ，e)的关系图

进一步发现集中化闭环供应链整体利润Π(Q*，e*)与分散化决策下零售商的最佳订货量Q*变化呈正比例关系，最佳订货量Q*与集中化闭环供应链整体利润Π(Q*，e*)的变动关系，如图4所示：

图4最佳订货量Q*与供应链利润Π(Q *，e*)的正比例关系图

因此，供应链的利润表达式为：

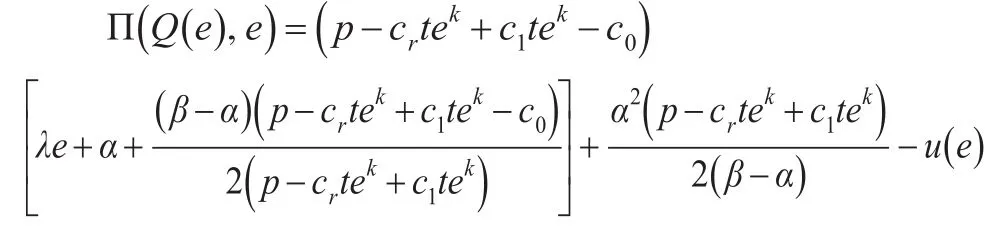
通过深入分析能够得到，在其他参数值固定不变的条件下，，零售商的最优努力水平e*和最佳订货量Q*，甚至是集中化闭环供应链系统的整体最大利润Π(Q*，e*)都与生产制造商采用新原材料的单位制造成本c0呈反比例关系；与市场需求的需求弹性敏感系数λ呈正比例关系，随着λ的增加而上升；与零售商的单位回收成本cr呈反比例关系；与产品的零售价格p的变动呈正比例关系；与回收努力水平弹性k呈反比例关系。同样可以分析出，在限制性补贴契约前提下实现整个闭环供应链的协调过程中，制造商给予零售商的回收补贴与生产制造商再制造过程中节约的单位成本c1呈正比例关系，而其给予零售商的关于超出目标订货量的数量给予的补贴与生产制造商使用新原材料生产的单位生产成本c0呈反比例关系。由此表明：生产制造商和零售商在闭环供应链废旧产品再制造的协调过程中，应当充分考虑生产制造商采用新原材料的单位制造成本c0、零售商的单位回收成本cr、市场需求弹性λ、回收努力水平弹性k、产品的零售价格p以及生产制造商再制造过程中节约的单位成本c1等因素来确定最优努力水平e*和最佳订货量Q*，获得最大的期望利润，从而使整个闭环供应链实现协调运作。其影响因素之间的变动关系，如表2所示：

表2 影响因素的变动关系

5 结论

本文以努力水平影响需求前提下闭环供应链上废旧产品的回收再制造为切入点，讨论了由制造商和零售商组合的两级闭环供应链的协调问题，构建了闭环供应链上制造商与零售商之间的博弈模型，分析了零售商努力水平与订货量同时协调情况下来实现闭环供应链协调运作，指出制造商对废旧品进行简单地回收再制造行为无法实现整个闭环供应链的协调，而基于限制性补贴的供应链契约在满足一定的参数契约的基础上能够实现供应链协调。在此基础上，给出模型的优化方法，进一步分析相关因素对供应链协调产生的效用及相互之间的变动关系。研究表明：制造商和零售商在闭环供应链废旧产品再制造的协调过程中，应当综合考虑零售商的努力水平、制造商采用新原材料的单位制造成本、市场需求弹性敏感系数、零售商单位回收成本、回收努力水平弹性系数、产品的零售价格以及制造商再制造过程中节约的单位成本等因素来实现努力水平和订货量的同时协调，以获得最大的期望利润，从而，使整个闭环供应链能够实现协调运作。最后，通过数值计算分析论证了推理的合理性与有效性，但是数值分析显示努力水平与订货量同时协调时，供应链并不能获得最大利润，其具体原因有待进一步探讨。

[1]王迎军.供应链管理实用建模方法及数据挖掘[M].北京：清华大学出版社,2001.

[2]Gulera M G,Bilgic T.On Coordinating an Assembly System Under Random Yield and Random Demand[J].European Journal of Opera⁃tional Research,2009,196(1).

[3]Chen J,Zhang H,Sun Y.Implementing Coordination Contracts in a Manufacturer Stackelberg Dual-Channel Supply Chain[J].Omega, 2012,40(5).

[4]孙荣庭等.考虑零售商竞争的供应链契约选择模型[J].运筹与管理, 2011,20(5).

[5]徐琪.价格相关需求下基于回购与价格弹性联合契约的供应链协调[J].预测,2011,30(4).

[6]Savaskan R C,et al.Closed-Loop Supply Models With Product Reman⁃ufacturing[J].Management Science,2004,50(2).

[7]赵晓芳,赵晓敏.基于产品差异的闭环供应链绩效分析[J].上海理工大学学报,2011,33(5).

（责任编辑/易永生）

F270

A

1002-6487（2016）24-0046-04

国家自然科学基金资助项目(71171135)；沪江基金资助项目（A14006）；上海市一流学科建设项目(S1201YLXK)；上海高校青年教师培养资助计划项目（slg14020）；上海理工大学博士启动项目(1D-10-303-002)；上海理工大学人文社会科学研究项目(12XSY09)；上海理工大学国家级项目培育课题（15HJPY-QN09）

何建佳（1981—），男，湖南道县人，博士，讲师，研究方向：管理科学、供需网及其管理、超网络。

蒋雪琳（1990—），女，安徽灵璧人，硕士，研究方向：物流、供应链管理及企业合作。

徐福缘（1948—），男，浙江绍兴人，教授，博士生导师，研究方向：系统工程、供需网及其管理。